基于LightGBM算法的25 Hz相敏轨道电路故障诊断方法优化

李长春，赵林海

(北京交通大学 电子信息工程学院, 北京 100044)

25 Hz相敏轨道电路是我国铁路信号控制领域的重要基础设备，因具有抗干扰能力强、应变速度快和防雷性能好等优点[1]，在我国既有线站内广泛使用。由现场调研可知：一方面，该轨道电路受周围环境影响较大，故障具有多杂且组合故障不易判别等特点[2]；另一方面，现阶段信号集中监测系统(Centralized Signal Monitoring System，CSM)仅监测了25 Hz相敏轨道电路轨道继电器的轨道电压信号与相位差信号[3]，使得在此基础上的故障诊断系统存在诊断效率不高等问题[6-13]。由此可见，对于现有CSM，迫切需要针对其25 Hz相敏轨道电路的诊断方法进行优化，以满足铁路设备维护发展的要求。

在目前的研究中，文献[4-5] 设计了一种25 Hz相敏轨道电路故障诊断专家系统；文献[6]提出了基于模糊神经网络的25 Hz相敏轨道电路故障诊断方法，而文献[7-9]在此基础上进行了方法的优化；文献[10]提出了基于模糊决策树的25 Hz相敏轨道电路故障诊断方法；文献[11-12]提出了基于方法组合的25 Hz相敏轨道电路故障诊断方法；文献[13]提出了基于SA-BP神经网络的25 Hz相敏轨道电路故障诊断方法[6-7,10，12-13]。

以上方法虽然在一定程度上提高了对25 Hz相敏轨道电路的故障诊断性能，但仍存在两方面的不足。一方面，文献[6-7,10，12-13]所提方法需要在室外设备上增加两个电压监测点，这使其采集的信号容易受室外环境变化的影响，且采用电压监测方式需将相应监测设备接入到轨道电路中，可能带来安全隐患。另一方面，目前的诊断方法，如文献[4-13]所提方法主要是利用专家经验和数据驱动，故需要基于长期的经验总结和大量的数据采集工作，且没有给出一些如组合故障等非常见故障的诊断策略。

针对上述研究不足，本文首先采用电流监测方式，将轨道电路室内所有可行的电流监测点加入原CSM监测方案中，构成初步监测方案，并利用传输线理论对所有可监测信号进行建模。然后，使用故障注入技术[14]对各常见故障模式下的监测信号进行仿真，构建故障数据集，生成相应故障诊断模型，并基于模型的性能，进行监测信号的筛选，对初步监测方案进行优化。最后，设计包含诊断阈值与诊断模型再训练过程的故障诊断策略。实验表明，本文方法只需增加对送电端电源屏输出电流的监测，便可实现对25 Hz相敏轨道电路14种常见故障的精确诊断，并可实现对非常见故障的预判、再学习与诊断。本文方法可有效提升CSM对25 Hz相敏轨道电路的故障诊断性能，能够满足铁路现场对25 Hz相敏轨道电路的使用和维护要求。

1 25 Hz相敏轨道电路结构及其基于CSM的故障诊断

图1为25 Hz相敏轨道电路的总体结构，其可分为送电端设备、受电端设备和钢轨线路三个部分。其中，送电端主要包括送电端扼流变压器和送电端轨道变压器等设备；受电端主要包括受电端扼流变压器、受电端轨道变压器、防雷补偿单元、防护盒和轨道继电器等设备。

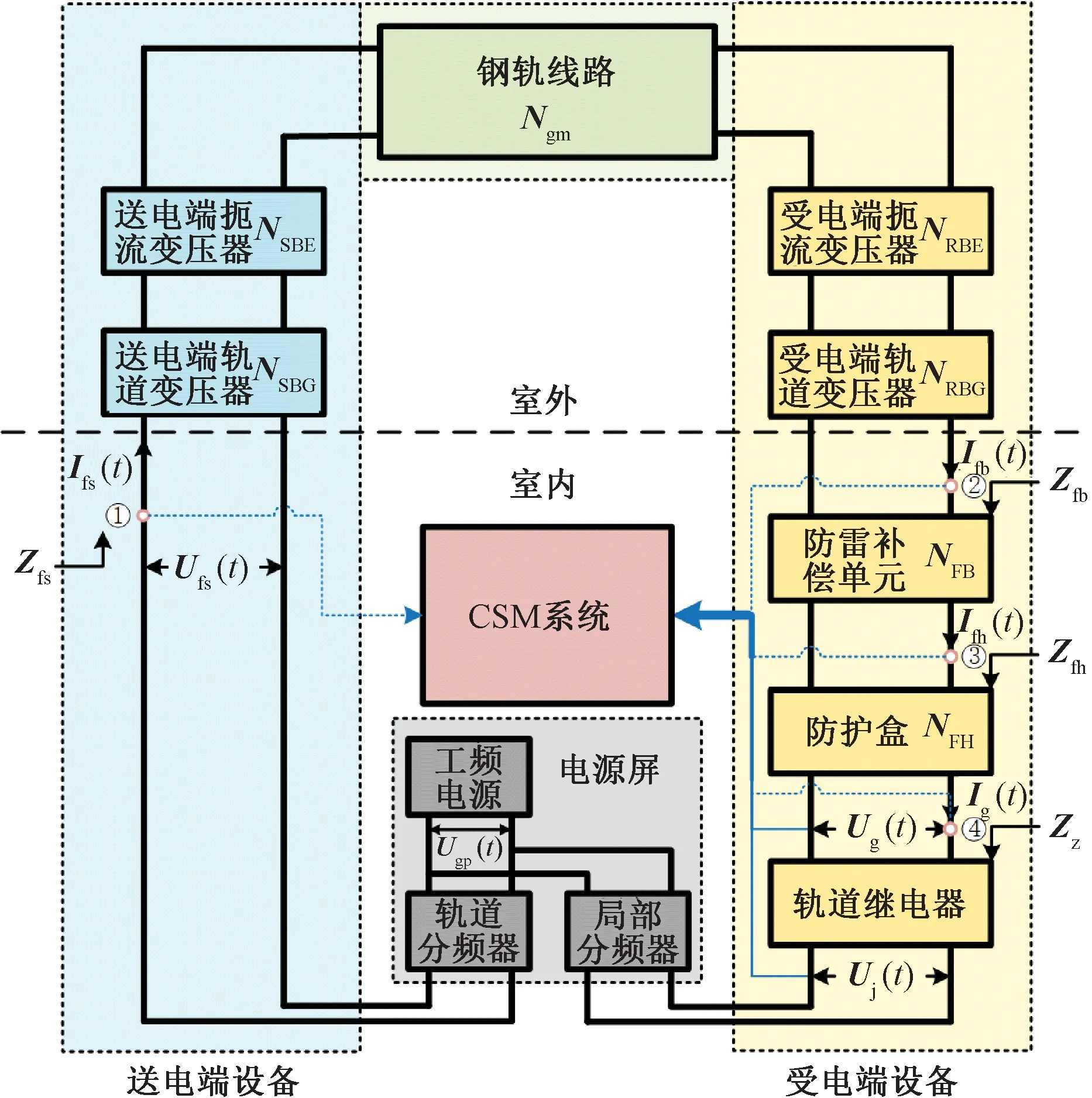
图1 25 Hz相敏轨道电路总体结构

图1中，工频电源Ugp(t)分别经轨道分频器和局部分频器产生轨道电源Ufs(t)和局部电源Uj(t)，且Uj(t)在相位上超前Ufs(t)90°。其中，对于Ufs(t)，其经送电端电缆由室内传输到室外，并经送电端轨道变压器和送电端扼流变压器后沿钢轨线路进行传输，再经受电端扼流变压器和受电端轨道变压器送至室内，最后经防雷补偿单元与防护盒后，到达轨道继电器的轨道线圈，形成相应的轨道线圈电压信号Ug(t)。对于Uj(t)，其直接在室内通过电缆接入到轨道继电器的局部线圈，形成相应的局部线圈电压Uj(t)。对于轨道线路空闲，设备完好的调整状态，若Uj(t)和Ug(t)间的相角和二者的幅度满足要求[6]，则轨道继电器将励磁吸起；对于有列车占用的分路状态，由于列车轮对分路的影响，Uj(t)和Ug(t)将不能满足上述要求，故将使轨道继电器失磁落下。

对于CSM，其在25 Hz相敏轨道电路内设了两个监测点，以实时采集Ug(t)和Uj(t)，并计算两信号的相位差，最终实现对轨道继电器轨道线圈电压Ug(t)和相位差φ(t)的实时监测。

2 基于传输线的25 Hz相敏轨道电路的建模与验证

经调研发现，基于上述两监测信号的诊断方法，对许多常见故障，如送电端扼流变压器钢轨侧电缆接触不良等，都不能实现诊断。同时，考虑室外天气和环境温度影响，以及电压接入式监测对系统造成的安全隐患，本文采用电流监测方式，将所有可行的电流监测点加入原CSM监测方案中，即在现阶段CSM可监测的轨道继电器轨道线圈电压Ug(t)、局部线圈电压Uj(t)以及两电压的相位差φ(t)的基础上，增加对①送电端电源屏输出电流Ifs(t)、②防雷补偿单元输入电流Ifb(t)、③防护盒输入电流Ifh(t)和④轨道继电器轨道线圈电流Ig(t)这4个信号的监测，构成本文的初步监测方案。

2.1 监测信号的建模

下面利用传输线理论[15]，对调整状态下上述各监测信号进行建模。

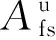
Ufs(t)与Uj(t)的数学表达式分别为

( 1 )

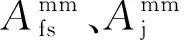
( 2 )

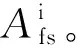
Ifs(t)与轨道电源Ufs(t)之间的关系为

Ifs(t)=Ufs(t)/Zfs

( 3 )

式中：Zfs为由监测点①向轨道继电器的视入阻抗，即

Zfs=(Ngh11×Zz+Ngh12)/(Ngh21+Ngh22)

( 4 )

式中：Zz为轨道继电器的输入阻抗；Ngh11、Ngh12、Ngh21和Ngh22为由监测点①至防护盒的传输特性等效四端网络Ngh的参数，即有

NSBG×NSBE×Ngm×NRBE×NRBG×NFB×NFH

( 5 )

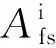
( 6 )

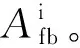
由送电端轨道变压器至受电端轨道变压器的传输特性等效四端网络Ngg可表示为

( 7 )

可求得Ifb(t)与Ufs(t)之间的关系为

Ifb(t)=Ufs(t)/(Ngg11×Zfb+Ngg12)

( 8 )

式中：Zfb为从防雷补偿单元向轨道继电器的视入阻抗，即

Zfb=(Nbh11×Zz+Nbh12)/(Nbh21+Nbh22)

( 9 )

其中：Nbh11、Nbh12、Nbh21和Nbh22为由防雷补偿单元至防护盒的传输特性等效四端网络Nbh的参数，即

(10)

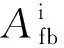
(11)

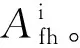
由送电端轨道变压器至防雷补偿单元的传输特性等效四端网络Ngb可表示为

(12)

则Ifh(t)与Ufs(t)的关系可表示为

Ifh(t)=Ufs(t)/(Ngb11×Zfh+Ngb12)

(13)

式中：Zfh为从防护盒向轨道继电器的视入阻抗，即

Zfh=(NFH11×Zz+NFH12)/(NFH21+NFH22)

(14)

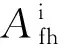
(15)

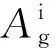
Ig(t)与Ufs(t)之间的关系可表示为

Ig(t)=Ufs(t)/(Ngh11×Zz+Ngh12)

(16)

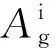
(17)

此外，由于Ug(t)与Ig(t)之间满足

Ug(t)=Zz×Ig(t)

(18)

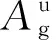
(19)

(6)相位差φ。

结合式(1)和式(19)，轨道继电器轨道线圈电压Ug(t)与局部线圈电压Uj(t)的相位差φ为

φ=φfs-φ(Ngh11+Ngh12/Zz)-φj

(20)

2.2 监测信号模型的验证

为验证所建模型的正确性，本文对站内97型25 Hz相敏轨道电路进行了测试，其主要设备为BG2-130/25型轨道变压器，BE2-600/25型扼流变压器，FB-2型防雷补偿单元，HF-2型室内防护盒，JRJC-70/240型轨道继电器，钢轨线路(长度200 m)，限流电阻(4.4 Ω)，道砟电阻(1.0 Ω·km)。

将上述设备参数输入所建模型中即可得到各监测量的仿真值，其与测量值的对比结果如表1所示。

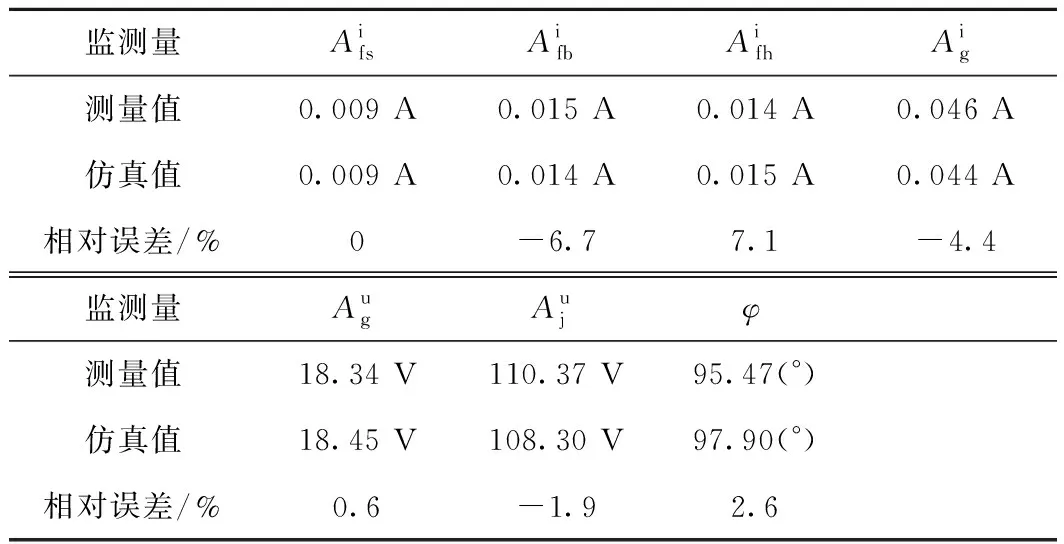
表1 测量值与仿真值的对比

由表1可以看出，基于模型的仿真值与现场测量值较为接近，相对误差的绝对值均在7.1%以下，这表明所建模型是可靠的，可准确表征各监测信号。

3 基于LightGBM算法的25 Hz相敏轨道电路故障诊断方法

3.1 故障诊断流程

为实现对初步监测方案的改进以及对25 Hz相敏轨道电路故障的智能诊断，设计一种基于LightGBM算法的故障诊断方法，其方法流程见图2，可分为故障数据集的构建、故障诊断模型的生成和故障诊断策略的设计3个部分。

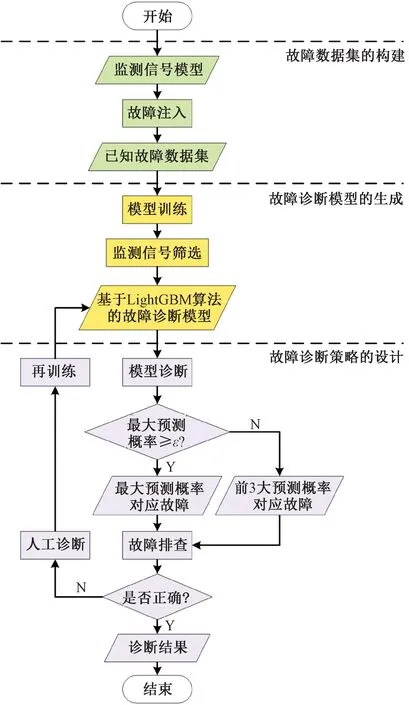
图2 基于LightGBM算法的25 Hz相敏轨道电路故障诊断方法流程

具体流程共分5步：

Step1基于所建各监测信号模型，采用故障注入技术进行各监测信号的仿真，构建常见故障数据集，并将常见故障数据集划分为训练集、验证集和测试集。

Step2基于LightGBM算法使用训练集进行故障诊断模型的训练，使用验证集验证模型性能，并基于模型性能进行监测信号的筛选，生成相应的故障诊断模型。

Step3采用故障注入技术构建非常见故障数据集，并将其与测试集合并，构成故障合集。随后统计在不同阈值ε下，故障诊断模型对故障合集中常见和非常见故障样例的识别率，确定最佳诊断阈值ε*。

Step4对于最大预测概率大于阈值ε的样例，将其判为常见故障，并输出相应的故障类型；反之，则将其判为非常见故障，并输出前3大预测概率对应的故障类型，给后续的故障诊断工作提供参考。

Step5对输出故障类型进行排查，若正确，则输出诊断结果；若错误，则交由专家进行人工诊断，获取实际故障类型，并将人工诊断结果添加至训练集中进行模型的再训练，提升模型性能。

3.2 故障数据集的构建

经现场调查与文献研究[4-13]，25 Hz相敏轨道电路主要有分路不良和不正常红光带两种常见故障，其常见故障模式如表2所示。在此，轨道电路的正常状态(包括道砟电阻在正常范围内波动的情况)用E0表示。

表2 25 Hz相敏轨道电路常见故障模式

考虑轨道电路信号在传输过程中不可避免地会混入白噪声的干扰[18]，本文在信号的仿真过程中混入信噪比为10%的高斯白噪声[19]，即

SZ(t)=SO(t)+SN(t)

(21)

式中：SZ(t)为带噪声的信号；SO(t)为不带噪声的原信号；SN(t)为信噪比为10%高斯白噪声信号。

再结合所建模型，采用故障注入技术，即可构建常见故障数据集D。随后采用分层抽样法[20]即可将D划分为训练集DTR、验证集DVA和测试集DTE。

3.3 故障诊断模型的生成

LightGBM(Light Gradient Boosting Machine)[21]是一种使用基于树的学习算法的梯度提升框架，其在梯度提升决策树(Gradient Boosting Decition Tree, GBDT)[22]的基础上实现了多项优化，拥有训练速度快、准确率高以及泛化性能好等优点[23]。对于使用本文初步监测方案进行L类故障诊断的问题，基于该算法生成的故障诊断模型见图3。

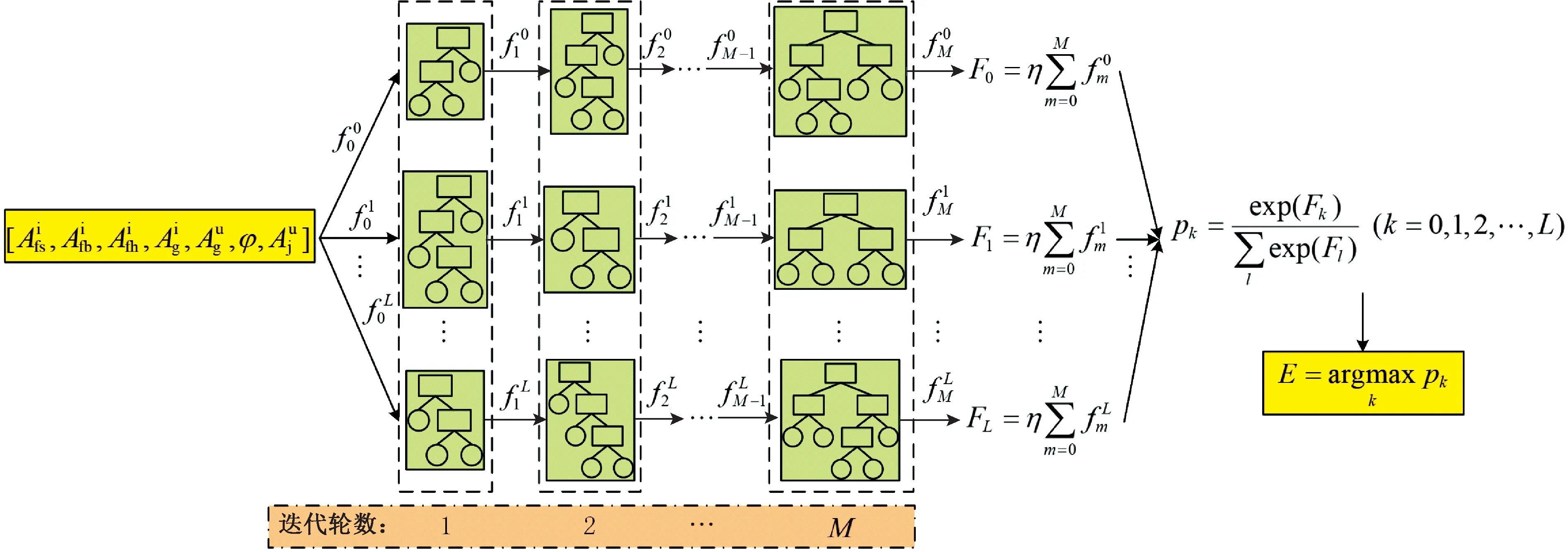
图3 基于LightGBM的25 Hz相敏轨道电路故障诊断模型示意图

3.3.1 模型的初始化

对于训练集

DTR={(xi,yi)}i=1,2,…,n

(22)

式中：xi代表第i个训练样本的输入，即

xi=[xi0xi1…xia…xi7]=

(23)

其中，a=0,1,…,7。

yi代表第i个训练样本的模式编号，即有

yi=kk=0,1,…,Li=1,2,…,n

(24)

则对yi进行one-hot编码有

(25)

对各树集成模型进行初始化有

(26)

3.3.2 决策树的生成

对于本文的故障诊断问题，模型的损失函数为

(27)

式中：pk(x)为使用归一化指数函数转化的第k个树集成模型Fk对于输入x的预测概率，即

(28)

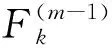
(29)

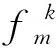
(30)

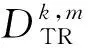
(31)

式中：des(D)为对数据集D进行降序排列；D[ns:ne]为选取数据集D中从索引ns到索引ne的数据；rand(D,N)为从数据集D中随机抽取N个样本组成新的数据集。

(32)

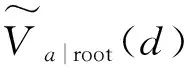
(33)

式中：

(34)

式中：I[·]为指示函数，含义是当·为Ture的时候，输出为1,当·为False的时候，输出为0； #D为集合D内元素数值。

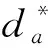
(35)

(36)

(37)

直到决策树的深度达到预设的最大深度s，则停止迭代，并令未分裂的Q个子结点成为叶结点，计算各叶结点的权重γqkm，即

q=1,2,…,Q

(38)

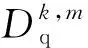
3.3.3 模型的更新

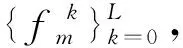
(39)

当模型迭代次数达到预设轮数M时，则生成了图3所示的故障诊断模型。

3.4 初步监测方案的改进

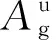
(40)

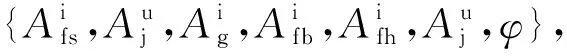
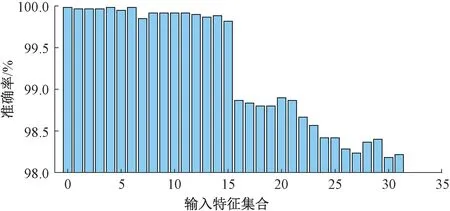
图4 各输入特征集合下的故障诊断准确率

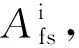
(41)

式(41)作为本文的监测方案进行25 Hz相敏轨道电路的故障诊断。此时，随机搜索的结果为M=20，η=0.1，s=7，模型在验证集上的故障诊断准确率可达到99.76%。

3.5 故障诊断策略设计3.5.1 诊断阈值的确定

为实现对非常见故障的判别，诊断方法设立了诊断阈值ε对模型输出的预测概率进行判断。为确定最佳诊断阈值ε*，本文对常见故障及其组合故障在不同阈值ε下的识别情况进行了统计。

考虑3种及3种以上故障同时发生的概率较低，本文首先对表2中常见故障进行了两两组合，并在除去相互矛盾的故障组合(如E1和E2)后，获得了86种组合故障类型。随后，使用故障注入技术，对每种组合故障各仿真了400组数据，构建了非常见故障数据集DUN，并将其与测试集DTE合并成为故障合集DC。最后在不同的阈值ε的情况下，使用故障诊断模型对故障合集DC进行了预测，并获得了不同阈值ε下模型对常见和非常见故障的识别率，结果见图5。

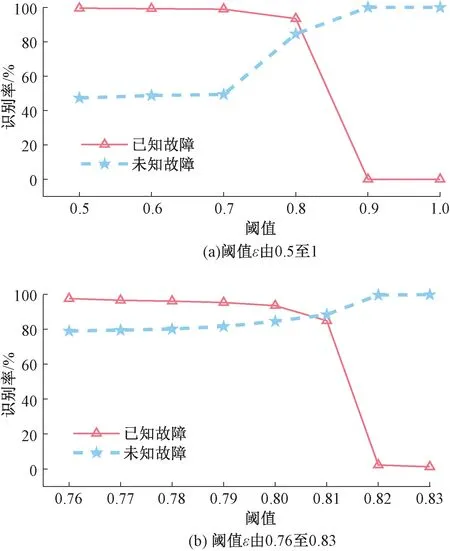
图5 不同阈值ε下模型对常见和非常见故障的识别率

由图5(a)可知，随着阈值ε的增加，模型对常见故障的识别率RRn在逐渐降低，对非常见故障的识别率RRu在逐渐上升。若令常见故障识别率的权重为α，非常见故障的权重为β，则最佳诊断阈值ε*可计算为

(42)

根据式(42)，工作人员可根据现场需求实时调整权重α和β的大小关系，对ε*进行更新。本文在此令α=β，则结合图5(b)可求得ε*=0.8，此时模型对常见故障的识别率为93.5%，对非常见故障的识别率为84.54%。

3.5.2 诊断结果的输出与诊断模型的再训练

确定最佳诊断阈值ε*后，为进一步提高现场诊断效率，当样本被判为非常见故障时，诊断方法将输出前3大预测概率对应的故障类型为后续的诊断工作提供参考；当样本被判为常见故障时，则直接输出最大预测概率所对应的故障类型。随后，工作人员可根据输出的故障类型对轨道电路进行故障排查。若实际故障的确为诊断方法输出的故障类型之一，则可确定诊断结果，并及时开展轨道电路的维修；若不是，则再让专业人员进行人工故障诊断，并将最后的人工诊断结果加入模型的训练集中，对模型进行再训练，提高模型对常见故障的诊断精度，同时对非常见故障进行学习，提升故障诊断模型的诊断性能。

4 实验验证

4.1 诊断方法功能验证4.1.1 常见故障诊断

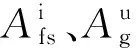
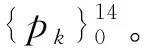
4.1.2 非常见故障诊断

首先，本文获取了3种不同类型的组合故障作为非常见故障，其类型如表3所示。

表3 非常见组合故障列表

然后，采用故障注入技术将这3种类型的故障分别注入轨道电路中，获得3组故障样本，再将其输入故障诊断模型中，即可得到其在各模式上的预测概率结果。该结果的前3大预测概率情况如表4所示。

表4 E15～E17故障样本诊断结果的前3大预测概率情况

由表4得，对于由常见故障E6和E13组合成的故障E15，其最大预测概率为p6=47.41%，小于阈值ε*(80%)，因此诊断方法将把其判为非常见故障，输出E6、E13和E12给现场的工作人员进行排查，而E6和E13的概率值远大于E12，且正是组成故障E15的常见故障，证明了故障诊断策略的有效性。

同理，对于由常见故障E2和非常见故障组合成的故障E16，其最大预测概率p2=73.47%，小于阈值ε*，诊断方法将输出E2、E9和E6这3种故障类型，且E2的概率值远大于E9和E6的概率值，因此，工作人员可优先排查故障E2，而E2正是E16的组成故障之一，证明故障诊断策略可提升现场的故障诊断效率。

对于由非常见的故障组合成的故障E17，其最大预测概率小于阈值ε*，且前3大预测概率值均较小，因此工作人员可根据该情况判断出现场发生了不常见故障。

最后，将表3中的非常见组合故障E15数据加入到模型的训练集中，对模型进行再训练，并采集一组该故障现场数据输入到模型中，获得模型最大预测概率为p15，概率值为81.14%，超过了诊断阈值ε*，将输出故障类型E15，与实际情况一致，证明了再训练过程的有效性。

4.2 诊断方法性能验证

为验证本文诊断方法的诊断性能，首先将本文方案与CSM现有方案相比较，其相应准确率见图6。

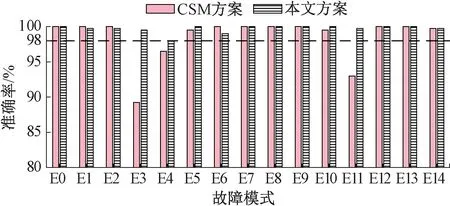
图6 CSM方案与本文方案在常见故障准确率上的对比

由图6可知，CSM在常见故障E3和E11上的准确率明显低于本文方案，分别为89.25%和93%。相比之下，本文方法在各常见故障模式上的准确率均在98%以上，且对于CSM方案准确率最低的故障E3，本文方法也达到了99.5%。可见，本文方法对各常见故障的总体识别率较高，且分布平均，优于CSM系统现有的诊断方法。

随后，将本文所用方法与文献[10]和文献[13]所用方法进行对比，见图7。

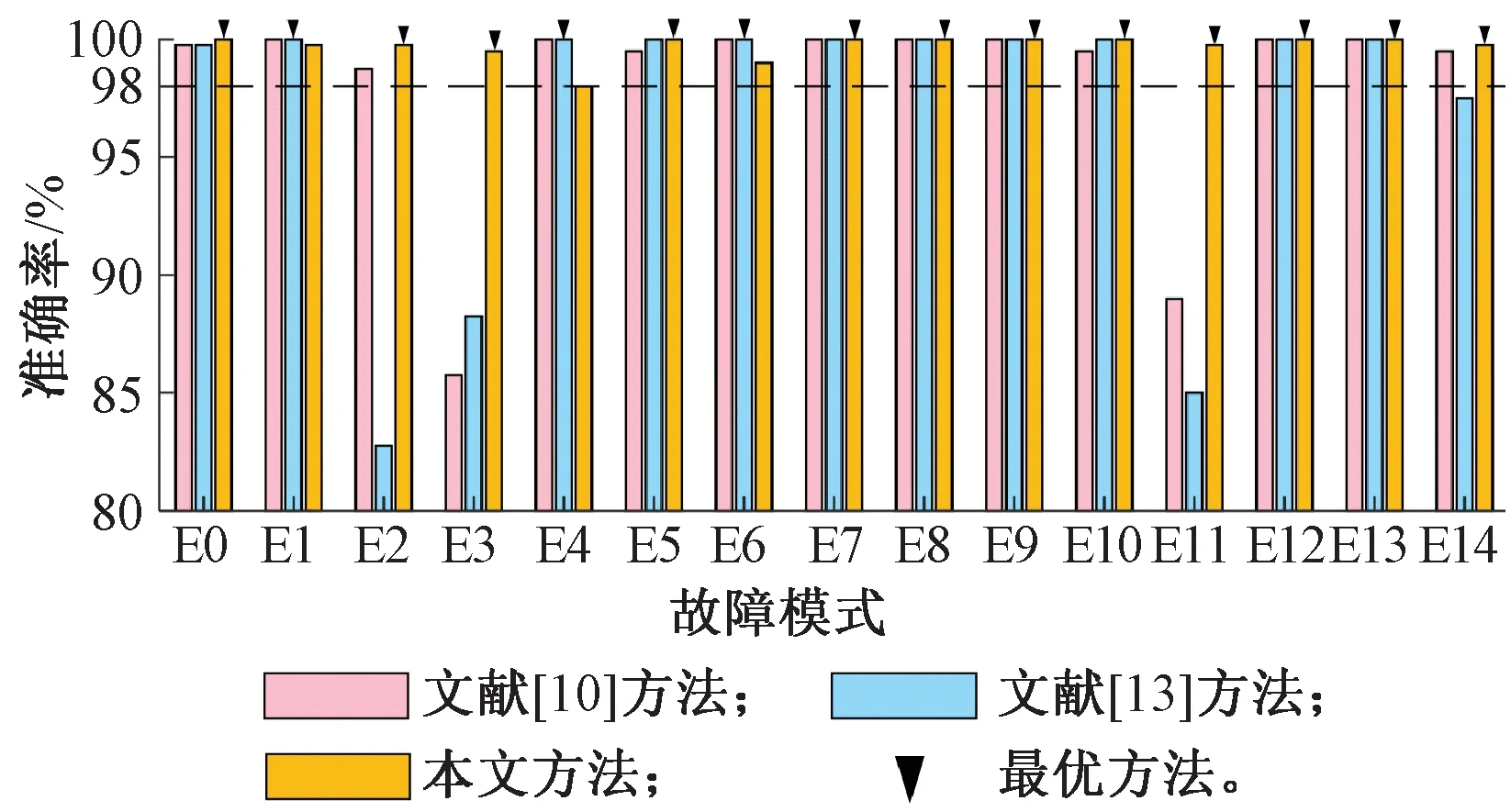
图7 本文方法与文献[10]和文献[13]方法在常见故障准确率上的对比

由图7可知，文献[10]所用方法在常见故障E3和E11上的准确率明显低于本文方法，分别为85.75%和89%；文献[13]所用方法在常见故障E2、E3和E11上的准确率明显低于本文方法，分别为82.75%、88.25%和85%。相比之下，本文所用方法在常见故障E2、E3和E11上的准确率可达99.75%、99.5%和99.75%，且在绝大部分故障模式上的准确率均优于其他两种方法，进一步验证了本文方法的性能。

5 结论

25 Hz相敏轨道电路是我国铁路信号设备的重要基础设备，其安全可靠的运行对保障行车安全、提高运输效率至关重要。因此，为提高该轨道电路的故障诊断性能，本文基于传输线理论和LightGBM算法对轨道电路的故障诊断方法进行了优化。首先，采用电流监测方式，将轨道电路室内所有可行的电流监测点加入原CSM监测方案中，构成本文的初步监测方案，并利用传输线理论对所有可监测信号进行建模。然后，使用故障注入技术对各常见故障模式下的监测信号进行仿真，构建故障数据集，生成相应故障诊断模型，并基于模型的性能，进行监测信号的筛选，并对初步监测方案进行优化。最后，设计包含诊断阈值与诊断模型再训练过程的故障诊断策略。

实验表明，本文方法只需增加对送电端电源屏输出电流的监测，便可实现对25 Hz相敏轨道电路14种常见故障的精确诊断，并可实现对非常见故障的预判、再学习与诊断，可有效提升CSM对25 Hz相敏轨道电路的故障诊断性能，满足铁路现场对25 Hz相敏轨道电路的使用和维护要求。