基于无缝切换技术的三相不平衡换相开关研究与设计
2022-09-14赵云龙车仁飞张牧烨陈家辉
赵云龙,车仁飞,张牧烨,陈家辉
(山东大学 电网智能化调度与控制教育部重点实验室,山东 济南 250061)
0 引言
配电台区三相电流不平衡主要是变压器出口侧三相负荷不平衡导致的,对变压器、输电线路以及用户人身财产安全造成不利的影响[1-3]。三相不平衡换相开关的出现,克服了传统无功补偿方法[4-5]只能补偿电网侧三相不平衡的弊端,可以保证线路整体平衡,有效控制了三相电流不平衡对配电网的不利影响。针对三相不平衡换相开关方面,已有专家学者开展研究。
目前,对于三相不平衡换相开关的研究主要在换相策略的软件设计方面,即对主控开关的换相策略控制算法的研究。文献[6]采用预计算控制策略,根据实时监测的负载数据,寻找最优化开关动作方案;文献[7]着重研究了优化算法的目标函数,使换相开关单元以较少的换相次数降低三相负荷不平衡度和线损;文献[8]建立了长效三相平衡优化换相模型,并采用模拟结晶算法对其求解,进而求得配电网负荷的最优换相方案。以上研究在换相指令的寻优过程取得了不错的效果,然而并未涉及分换相开关的相序切换方面。分换相开关的作用是完成相序在A、B、C 相之间的自由切换,由于相序之间存在120°的相位差,目前,该过程存在断电时间长,换相过程电压、电流畸变严重的问题。文献[9]采用模糊C 均值聚类算法对负荷进行分类,然后进行换相策略寻优,同时对相序切换方面进行了研究,然而换相执行元件仅采用继电器这一机械开关,断电时间长且不可控,而且触点断开时容易产生电火花,因而该方式缺陷较大。为了减少机械开关时间不可控的弊端,文献[10-12]在相序切换方面,换相执行元件采用基于半导体器件的固态开关与基于继电器的机械开关相结合的形式,通过经典的过零投切技术,实现负载电流过零切除、电压过零投入,断电时间可以控制在20 ms 以内,然而断电时间与负载的特性(容性、感性)有很大的关系,对一些敏感负载,如电子式日光灯、电感式日光灯、老式电饭煲、精密电机以及其他需要实时存储重要信息的场合(银行、互联网数据中心等),会造成不利的影响。为了进一步缩短切换时间,文献[13-15]对换相开关的过零切换方式进行改进,通过精确的时间延迟,精确控制固态开关导通的时刻,达到缩短断电时间的目的,时间可控且与负载性质关系不大。不过,负载电压、电流存在较大的畸变,且对于阻感或阻容负载而言,电压、电流突变会相互影响,对电网以及用户产生不利的影响。文献[16]采取在电压交点处切换的方式来实现无缝切换,但是该方法只能应用于纯阻性负载的切换,对于感性与容性负载无法得到期望的效果,并且该换相过程中电压、电流畸变也较为严重。以上研究仅仅考虑了如何缩短断电时间,并未考虑到负荷的性质以及电压、电流的畸变情况。对此,本文研究了一种新的无缝切换结构与换相流程,既减少了整流环节的电流谐波,又减少了电压跟踪阶段的频率偏差,并且采用全控器件取消了并网阶段,减少了换相时间与电流畸变含量,为三相不平衡换相开关应用于更加敏感的负荷提供了可能。
1 三相不平衡换相开关整体结构
三相不平衡换相开关主要由1 个主控开关和若干个分换相开关两部分组成,其整体结构图如附录A 图A1 所示。当确定配电网区出现严重的三相不平衡时,智能换相开关的主控开关根据各个分换相开关检测到的电流信息,按照预先设定好的换相寻优算法,确定合理的换相策略,然后给各个分换相开关下达换相指令,最后各个分换相开关根据收到的指令完成相序切换动作,进而合理地改变某些单相负荷的相序,使负荷在给定条件下达到三相平衡。
2 无缝切换研究
2.1 无缝切换整体结构
无缝切换的主电路如图1 所示。换相时,先经过一个过渡环节,使得将要相互切换的两相的电压调整为同幅、同频与同相,然后电力电子开关动作,达到无缝切换的目标,完成换相过程。本文所提出的无缝切换总体结构主要包括主控以及通信电路、电压和电流采集以及控制电路、换相执行元件、过渡环节、过渡执行元件等部分。其中过渡环节由整流及Boost 电路、逆变器电路组成,完成电压信号的整形和跟踪功能。为了保证换相的快速性,减少整个换相过程的时间,每相的换相执行元件由一对反向串联的IGBT 与继电器并联组成。在换相过程中,参与的器件为每一相的IGBT 对:导通时,由IGBT 与二极管配合完成,图中路径①和②分别表示换相执行元件的正向导通和反向导通;关断时,在IGBT 的关断触发信号的基础上由2 个反向串联的二极管完成。为了减少换相结束后IGBT 的通态损耗以及散热问题,只需关断IGBT 并导通与其并联的继电器即可。而过渡执行元件的作用是在换相过程将过渡环节产生的电压与市电电压进行隔离,目的是取消并网环节,进而减少电压、电流谐波以及整个换相过程的时间。
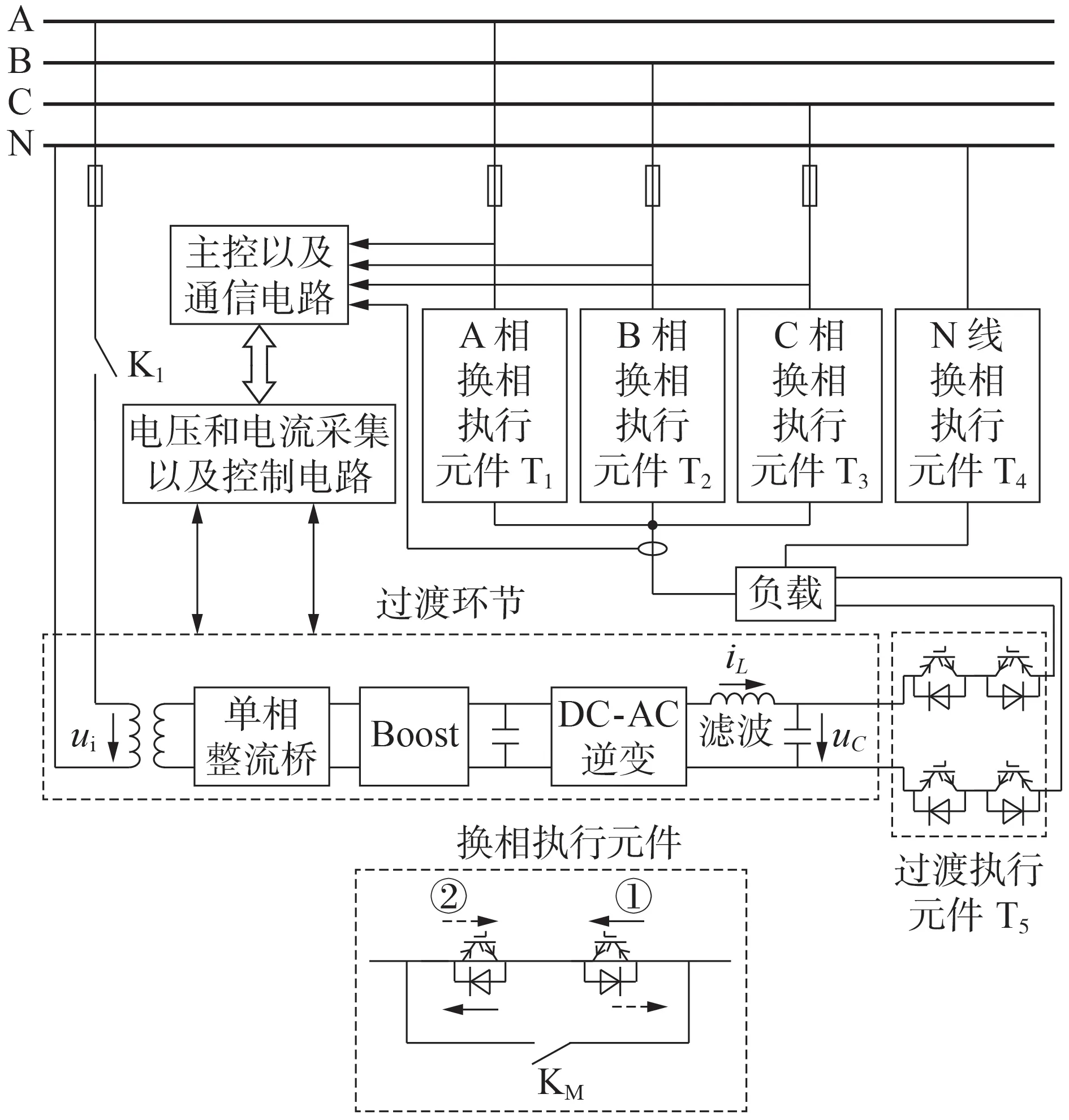
图1 无缝换相整体结构Fig.1 Overall structure of seamless commutation
这样,经过以上各个组成部分的相互配合,负载相序可以在A、B、C 相之间进行无缝切换。为了便于说明,本文将“当前相”定义为换相开关接收到主控开关传来的换相指令之前负载所在的相别;“切换相”是指换相开关根据主控开关传来的数据判断出的将要切换的相别;“不动相”是指A、B、C 三相除去“当前相”以及“切换相”所剩的相别。以A相切换到C相为例说明具体无缝换相流程。
1)初始阶段:换相开关接收到换相指令,确定A相为“当前相”、C相为“切换相”、B相为“不动相”,并将T1、T4的IGBT 对导通,随后断开与它们并联的继电器常开触点KM。
2)当前相跟踪阶段:A 相市电给负载供电,此时闭合K1,逆变器空载跟踪A相市电电压的频率、相位和幅值。
3)切换相跟踪阶段:此时逆变器的输出电压的频率、相位和幅值与A 相市电电压相同,关断T1、T4中的IGBT 对并导通T5,此时负载由逆变器供电,之后逆变器带载跟踪C相市电电压的频率、相位和幅值。
4)换相完成阶段:当负载电压的频率、相位和幅值与C 相市电电压相同时,断开T5,导通T3、T4中的IGBT 对,负载切换到C 相供电,随后导通T3、T4中的KM,短延时后断开T3、T4中的IGBT 对,最终换相结束,过渡环节退出运行。
经过以上步骤,可以达到无缝切换的目的,进而减少换相过程对电网与设备的不利影响,提高电能质量,为换相开关应用于更加敏感的负荷提供了可能。下面对过渡环节的几个主要部分进行说明。
2.2 整流以及Boost环节
整流以及Boost 环节的主要功能有2 个:一是为后面逆变环节提供较高的直流电压;二是进行功率因数的校正。必须要提高整流电路输出电压以补偿逆变器的电压损失,因此需要该环节Boost电路的升压功能。同时,该环节对于电网而言是一个大的谐波源,会导致输入侧电流波形畸变较为严重(尖峰脉冲),输入电流与输入电压的相位差会较大,输入侧的功率因数就会较低。因此,需要Boost电路的功率因数校正功能改善输入电流的波形,使其相位逐渐靠近输入电压的波形,降低输入电流的谐波含量,提高功率因数并稳定输出电压[17]。
2.2.1 整流以及Boost电路整体拓扑结构
实际上,整流以及Boost环节整体结构也可称为Boost 型功率因数校正电路拓扑结构,如图2 所示。图中:ui、ii分别为交流市电输入电压、电流;uo1为整流桥输出电压;iL为流经升压电感LAPFC的电流;CAPFC为滤波电容;uodc、iodc分别为负载电压、电流;uC、iC分别为电容电压、电流;ioc为Boost电路输出侧总电流;D1为升压二极管。
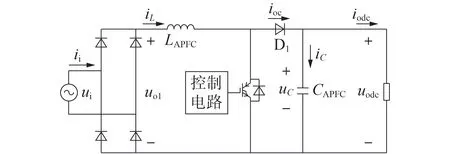
图2 整流以及Boost电路整体结构Fig.2 Overall structure of rectifier and Boost circuit
2.2.2 控制电路的控制策略选取
在电流连续导通(CCM)模式下应用最多的控制方式是直接电流控制,主要在对系统要求较高的大功率场合中应用,因此本文选取直接电流控制作为CCM 模式下电流的控制方式。在直接电流控制基础上的控制策略又可以分为平均电流控制策略、峰值电流控制策略以及滞环电流控制策略。相比其他2 种控制策略,平均电流控制策略具有电感电流的均值与输入电压的非线性误差都较小、抗干扰能力强的优点,并且应对负载的变化时其开关频率稳定性更强。因此本文采取平均电流控制策略。
平均电流控制策略的基本原理是对电流的平均值进行控制,采用基于电流环和电压环的双闭环控制方式,使得电流的相位逐渐趋向于输入整流电压的相位,以提高输入侧的功率因数。平均电流控制策略的原理图以及电感电流波形图见附录A 图A2。参考电流信号iref等于uo1的采样值与电压误差放大器输出值upc的乘积;然后将iref与电感电流的检测信号比较后再送入电流误差放大器,电流误差放大器的作用是对电流比较后所产生的具有较高频率的量进行平均化修剪;最后将经过电流误差放大器输出的平均电流误差与锯齿波进行比较产生IGBT 的脉宽调制(PWM)驱动信号Ug。当电感电流的检测信号值增加时,PWM 驱动信号的占空比将下降,电感电流随之下降,反之电感电流上升。
2.2.3 平均电流控制电压电流双闭环设计
1)电流环路设计。
由图A2可得电流环控制回路框图见图3。图中:Kio为电流误差放大器的增益;Kii为iL的采样增益。

图3 电流环控制回路框图Fig.3 Block diagram of current loop control circuit
Gic(s)为电流环控制器的传递函数,在此采用比例积分(PI)控制器,具体如式(1)所示。
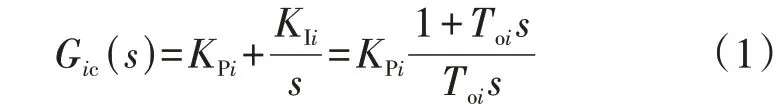
式中:KPi、KIi分别为电流环控制器的比例增益和积分增益;Toi为电流环控制器的积分时间常数。
Gid(s)为Boost电路小信号模型下得到的输入电感电流相对于占空比的传递函数,由于IGBT 的开关频率fk相比电网频率大得多,s=j2πfk很大,故可以进一步简化[18],具体如式(2)所示。

式中:Uodc为uodc的稳态量;R为负载的等效电阻;D′为IGBT关断时间与开关周期的比值的稳态量。
2)电压环路设计。
由图A2 可得电压环控制回路框图如图4 所示。图中:uref为参考电压信号;Kuo为uodc的采样增益。

图4 电压环控制回路框图Fig.4 Block diagram of voltage loop control circuit
Guc(s)为电压控制器(即PI 控制器)的传递函数,具体如式(3)所示。

式中:Kui为uo1的采样增益。
2.3 逆变环节
逆变环节的主要功能是进行电压波形的跟踪,包括当前相跟踪阶段和切换相跟踪阶段。
2.3.1 单相逆变器主电路拓扑结构
本文选取单相全桥式逆变器作为主电路的拓扑结构,如附录A 图A3 所示。根据前文所述,逆变系统在进行当前相跟踪阶段时处于空载状态,为了使输出滤波器更好地对系统受到的干扰信号(谐振频率附近)进行有效抑制,减少系统输出误差,提高当前相的跟踪效果,对LC 滤波器进行改进,在电容侧串联一个小电阻(Rn=0.1 Ω)构成LC 阻尼滤波器[19],改进后的空载时滤波电路的传递函数Glpf(s)为:
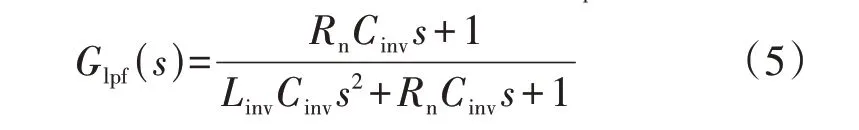
式中:Linv、Cinv分别为交流侧滤波电感、电容。
阻尼电阻的作用是将一个零点加入空载时的滤波电路传递函数,使得系统的性能得到了很大的提升:根轨迹左移、系统的稳定性提升以及调节时间减少。
2.3.2 控制策略选取
为了提高系统的快速性与跟踪精度,再根据前文所述的换相过程中逆变器的电压给定量是A、B、C三相市电电压,本文采用输出电压瞬时值控制策略。传统的逆变器采用PI 或比例积分微分(PID)控制器对电压或电流给定量进行跟踪,但是以上2 种控制策略在对交流信号的跟踪过程始终存在静差,且很难对较高频率的信号进行跟踪,而采用比例谐振(PR)控制器则可以最大限度地消除给定量与被控量之间的静差,实现理想的跟踪效果。然而,理想的PR 控制器只对单一的频率起作用,在实际的逆变器应用中,由于测量采样的不确定性,参考量的频率不会只固定在基波频率上,而是会有±1 Hz 的波动,并且无论是模拟设备或者是数字设备都无法实现此理想条件下的无限增益[20],因此在运用时会对理想的PR 控制器做一些变形,得到以下准PR 控制器的传递函数GPR(s)为:
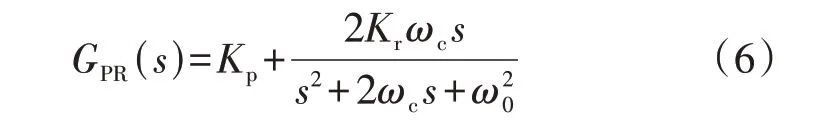
式中:Kp为比例系数;Kr为谐振系数;ω0为基波角频率;ωc为截止频率。
2.3.3 逆变器电压环设计
为了便于分析单相全桥逆变器的特性,现对图A3 所示的电路拓扑结构进行简化处理,得到的简化电路模型如图5 所示。图中:uinv为交流侧脉动电压;iLinv为流经滤波电感的电流;iCinv为流经滤波电容和阻尼电阻的电流;uoinv、ioinv分别为负载两端的电压与流经负载的电流;uCinv为滤波电容两端的电压;Z为负载等效阻抗。选取uinv、uoinv为状态变量,可得单相全桥逆变器控制系统的传递函数Ginv(s)为:
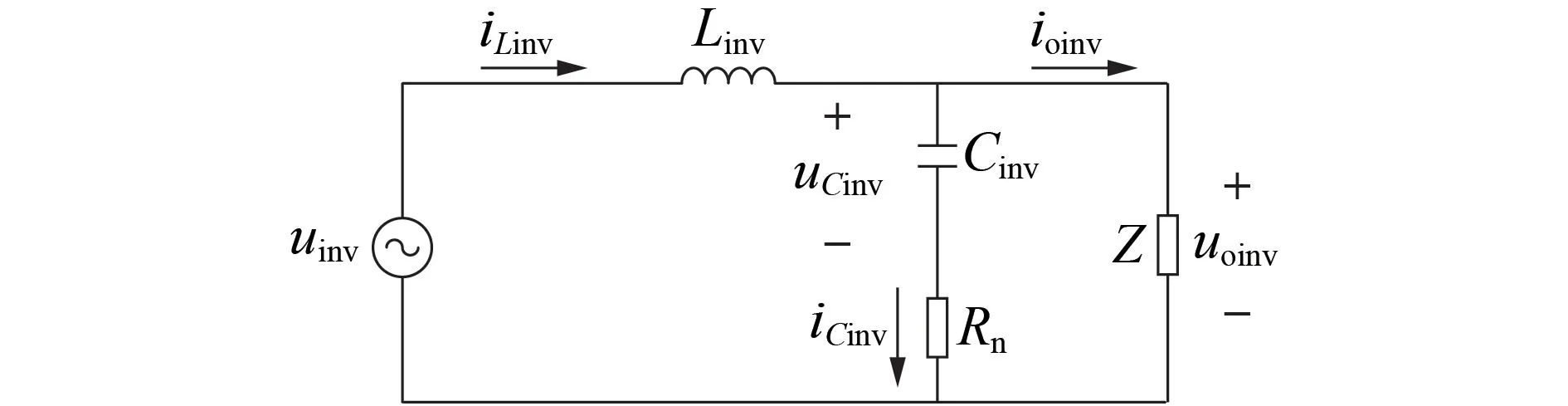
图5 单相全桥逆变器简化等效模型Fig.5 Simplified equivalent model of single-phase full bridge inverter

再结合前文所得准PR 控制器传递函数可得逆变器电压环整体框图如图6 所示。图中:uiref为市电电压给定量。

图6 逆变器电压环整体框图Fig.6 Overall block diagram of inverter’svoltage loop
3 仿真分析与实验验证
3.1 仿真分析
在Simulink 环境中搭建整体无缝切换环节电路仿真模型,主要包括整流以及Boost 电路模块、换相控制单元、换相执行元件模块、跟踪以及PWM 产生单元、单相桥式逆变器、负载等。具体仿真参数见附录A表A1。
3.1.1 逆变跟踪环节仿真分析
负载设置为2 Ω+2 000 µF 的阻容性负载(与纯阻性和阻感性负载相比较,阻容性负载电流受电压影响较大,因此更具有说服力),[0,0.1)s内,逆变器输出电压给定量1 为u1(t)=311sin(ωt),[0.1,0.2]s内给定量2 为u2(t)=311sin(ωt-2π/3),0.1 s 时刻给定量变化时逆变器输出电压波形如图7(a)所示。从图中可以看出,逆变器经过4 ms 左右的响应时间后可有效跟踪给定量2,但是这样直接切换给定量会造成电压、电流出现较大程度的畸变,此时逆变器输出电压、电流(即负载电压uoinv、电流ioinv)的总畸变率(THD)分别为109.79%、111.88%,在实际换相过程中会对负载产生不利影响,所以需要对此跟踪过程进行改进。
由于实际换相过程的给定量1(当前相)与给定量2(切换相)相位相差固定的2π/3 rad,因此可以在逆变器输出电压跟踪给定量u2(t)之前,先跟踪给定量u′2(i),具体如式(8)所示。

采样周期设置为Tcinv=1µs,则一共需要大约Tg=nTcinv=1.047 s 的 时 间 跟 踪u′2(i),由 于Tg时 间 后逆变器输出电压与u2(t)几乎一致,再跟踪u2(t)可以极大地消除前文所述直接跟踪u2(t)时出现的电压畸变现象。改进跟踪过程的逆变器输出电压、电流(即负载电压uoinv、电流ioinv)波形如附录A 图A4 所示,且图7(b)为u1(t)到u′2(i)切换点波形,图7(c)为u′2(i)到u2(t)切换点波形。从图中可以看出,在0.1 s时开始对给定量的跟踪,1.2 s之前跟踪结束(先跟踪u′2(i)再跟踪u2(t)),整个跟踪过程电压波形平滑,逆变器输出电压、电流畸变率仅分别为2.48%和2.46%,且2 个切换点处电压、电流的畸变率分别为0.65%(电压)、0.56%(电流)和0.73%(电压)、0.74%(电流),明显优于直接切换过程。其中在跟踪u′2(i)时会必然导致一定的频率偏差Δf,可由式(11)近似计算得到。


图7 跟踪过程切换点波形图Fig.7 Waveforms at switching point during tracking process
3.1.2 整体无缝切换环节仿真分析
以最常见的阻感负载(2 Ω+4 mH)为例,附录A图A5 为从A 相到C 相整个换相过程负载电压、电流以及切换控制脉冲波形,图8(a)为阻感负载情况下市电到逆变器切换点(上图)和逆变器到市电切换点(下图)周围1 个周期的电压波形快速傅里叶变换(FFT)分析图;附录A 图A6 为阻感负载情况下整流电路输入电压、电流和功率因数波形;图8(b)、(c)分别为阻感负载情况下输入电流波形及其FFT分析图。0.1 s 是市电供电到逆变器供电的切换点,1.153 s是逆变器到市电供电的切换点。[0,0.1)s包括初始阶段和当前相跟踪阶段:初始阶段是指换相开关接收到换相指令,确定“当前相”为A 相、“切换相”为C 相、“不动相”为B 相;当前相跟踪阶段是指逆变器空载跟踪A 相市电电压uSA的频率、相位和幅值。[0.1,1.153)s 是切换相跟踪阶段,此时负载由逆变器供电,逆变器带载跟踪C 相市电电压uSC的频率、相位和幅值;1.153 s 之后是换相完成阶段,当负载电压的频率、相位和幅值与C 相市电电压相同时,负载切换到C 相市电供电并最终换相结束,过渡环节退出运行。从图A5中可以看出,整个切换过程负载电压、电流波形平滑,只是在市电到逆变器切换点处由于阻感负载电压与电流之间相位差的存在,电压过零点时刻电流并非为0,所以在切换点处逆变器输出电压会有0.2 ms 时长的小幅畸变。而从图8(a)中可知,阻感负载情况下市电到逆变器切换点处的电压畸变率为0.80%,该小幅畸变对负载的影响可以完全忽略;逆变器到市电的切换点处负载电压畸变率为0.30%,该小幅畸变也不会对负载产生不利的影响。从图A6中可知,整流侧输入功率因数在0.99 以上;从图8(c)可以看出,输入电流畸变率在5%以下,满足电能质量要求。总而言之,从整体换相过程来看,本文所设计的无缝切换环节具有较高的跟踪精度以及换相可靠性,完全适用于三相不平衡换相开关对负载侧三相不平衡的治理。
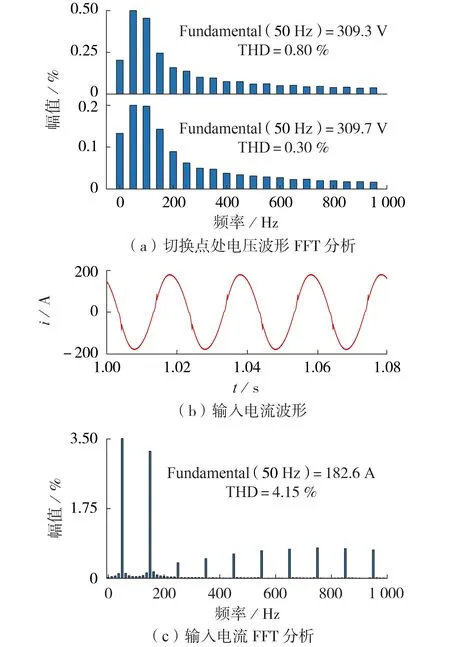
图8 阻感负载换相过程FFT分析Fig.8 FFT analysis of commutation process of resistive-inductive load
3.2 实验验证
对本文研究的无缝切换方案搭建实验平台进行验证,采用STM32F103ZET6 作为主控制器,主要负责信息采集、运算、控制等功能。
实验平台结构图与实验平台实物图分别见附录A 图A7、A8,主要包括主控处理器、A/D 采样模块、IGBT 驱动电路、无线通信电路、霍尔传感器以及过渡环节各部分元件。
同样以A 相切换到C 相为例,完成相序无缝切换的控制程序流程见附录A图A9。
设置实际负载为200 Ω+4 mH,接示波器测量得到无缝切换实验波形如附录A 图A10 和图9 所示。其中:图A10 表示阻感负载情况下整个换相过程负载电压、电流波形图;图9 表示阻感负载情况下市电到逆变器切换点和逆变器到市电切换点处负载电压与电流以及当前相与切换相电压波形。从图中可以看出,实际切换波形与仿真波形基本一致,只是实际电容充电时间较长,使得整体换相过程所需时间要长一些。
4 结论
针对当前三相不平衡换相开关相序切换过程中存在的断电时间长、电压和电流畸变严重的问题,本文在分换相开关方面提出了一种无缝切换方案:在输入侧,采用功率因数校正电路减少了输入电流的畸变量,提高了整套装置的功率因数;在输出侧,采用新的电压跟踪策略,使得跟踪过程的频率偏差小于0.5 Hz,采用IGBT 全控器件取消并网环节,减少了换相时间,真正实现了不间断供电并进一步减少了电压、电流的畸变量。通过仿真与搭建实验平台验证了上述方案的可行性。本文所提无缝换相与常规换相相比,增加了电力电子环节,使得成本有所提高,适用于前文所述的敏感负荷或对供电电压要求更高的场合。
附录见本刊网络版(http://www.epae.cn)。
