改进樽海鞘群算法的永磁同步电机多参数辨识

张铸， 张仕杰， 饶盛华,， 张小平， 王静袁

(1.湖南科技大学 信息与电气工程学院，湖南 湘潭 411201； 2.湖南科技大学 海洋矿产资源探采装备与安全技术国家地方联合工程实验室，湖南 湘潭 411201)

0 引 言

永磁同步电机(permanent magnet synchronous motor,PMSM)以其功率密度高、响应速度快、运行效率高等优点被广泛应用于新能源汽车、工业制造、机器人和风力发电等领域[1-2]。由矢量控制理论可知，PMSM优异的控制性能依赖于定子电阻、交直轴电感和永磁体磁链等电机参数的准确获取，然而在电机运行过程中上述参数会受到温度升高、磁场饱和以及负载扰动等多因素的影响[3]，从而偏离原始设计值，造成电机控制性能和运行效率降低。

为此国内外诸多学者对不同的PMSM参数辨识方法进行了深入研究。文献[4-5]提出了基于最小二乘法的参数辨识方法，该方法简单且易实现，但算法的运算量较多，数据需要的存储空间大，且转速波动和测量噪声对求导结果有较大的影响。文献[6-7]提出了基于模型参考自适应算法的参数辨识方法，该方法需要分步进行参数辨识，但后辨识的参数容易受到先辨识参数的影响，且辨识参数初值的选取对辨识结果影响较大。文献[8]采用了卡尔曼滤波算法进行参数辨识，但需要先知道其他电机参数，影响了参数辨识的鲁棒性，且需要进行大量矩阵和矢量运算，过程复杂。文献[9]提出了一种变步长自适应神经网络算法进行参数辨识，辨识结果较优，收敛速度较快，稳态误差较小，但运算量过大，在实际中运用的难度较大。

针对传统辨识算法存在的诸多问题，国内外学者将一些元启发式优化算法应用于PMSM参数辨识中，为后续学者在电机参数辨识上提供了新的研究方向。文献[10]采用了遗传算法能同时辨识定子电阻、dq轴电感和永磁体磁链四个参数，但该算法计算量较大且容易陷入局部最优。文献[11]提出了一种基于柯西和高斯变异的改进珊瑚礁算法进行参数辨识，不过该方法也容易陷入局部最优，且寻优的速度和精度都有待加强。文献[12]提出了一种基于柯西变异粒子群算法的参数辨识方法，该算法简单，控制参数容易选择，但在辨识模型欠秩情况下辨识参数缺乏依据。文献[13]提出了一种基于免疫完全学习型粒子群算法的参数辨识方法，该方法在研究基础上引入人工免疫系统，在全局搜索以及局部收敛方面的性能得到提高。文献[14]提出了一种改进综合学习粒子群算法的参数辨识方法，该方法在综合学习粒子群算法的基础上引入了增长率算子以及高斯扰动，改善了算法的辨识效果，提高了局部搜索的能力。

2017年Mirjalili博士等人提出了樽海鞘群算法(slap swarm algorithm，SSA)[15]，这是一种新型的元启发式算法，该算法机制简单，计算量小且易于实现，但存在种群多样性差且在迭代后期不能进行精确寻优等缺点。本文将樽海鞘群算法应用于PMSM参数辨识，同时针对SSA在求解复合问题时容易陷入局部最优的缺点，引入自适应正态云模型，提出一种基于自适应正态云模型的樽海鞘群优化算法(cloud SSA，CSSA)。该算法在追随者位置更新加入正态云模型，提高种群的多样性，改善SSA易陷入局部最优的缺点，同时通过自适应调整正态云模型熵值，随着迭代次数的增加，使后期随机性和模糊性随之减小，提高局部寻优的能力。最后基于同步旋转dq轴坐标系下的PMSM辨识模型，使用CSSA对PMSM参数进行辨识。

1 PMSM数学模型

在忽略PMSM的涡流损耗以及铁损耗的情况下，PMSM在同步旋转坐标系(dq坐标系)下的定子电压方程为：

(1)

式中：ud、id为定子直轴的电压电流；uq、iq为定子交轴的电压电流；ωr为电角速度；Rs为定子电阻；Ld、Lq为定子直轴、交轴电感；ψf为永磁体磁链。

在稳定情况下，近似认为did/dt=0、diq/dt=0，则dq坐标系下的PMSM的离散电压方程为：

(2)

表贴式永磁同步电机一般使用id=0的矢量控制方式进行解耦控制，从式(2)中可看出方程组含有4个未知参数(Rs、Ld、Lq、ψf)，方程组的秩为2，此时方程组有无数组解。目前许多学者都采用在d轴注入id≠0的负序弱磁电流策略，进而得到一个四阶满秩的永磁同步电机辨识模型：

(3)

式中：下标带‘0’的变量表示在id=0控制策略下，下标中无‘0’的变量则表示在id≠0的控制策略下；带‘^’的变量和参数为辨识值，反之则为实际值。

两种控制方式下的数据采集如图1所示，式(3)中id0(k)、iq0(k)、ωr0(k)为a～b时间段第k次采集数据，id(k)、iq(k)、ωr(k)为c～d时间段第k次采集数据。

图1 数据采集Fig.1 Data acquisition

2 基于正态云模型的樽海鞘群算法

2.1 标准樽海鞘群算法

SSA算法源于对樽海鞘群捕食行为的研究。在捕食过程中，樽海鞘链由前端的领导者引导，后端的跟随者追随其先前的个体，集体向食物移动。

种群随机初始化公式如下：

XN×D=rand(N,D)×(ub-lb)+lb。

(4)

式中：N为樽海鞘群的种群规模；D为空间维度。

樽海鞘领导者的位置更新公式如下：

(5)

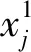
(6)

式中：t为当前迭代次数；Tmax为最大迭代次数。

根据牛顿运动定律来更新樽海鞘跟随者位置，公式如下：

(7)

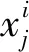
(8)

2.2 正态云模型

云模型的概念由李德毅院士于1995年提出[16]，可以实现定量数值与定性概念之间的不确定转换，模型能很好地描述和处理数据的模糊性和随机性。正态云模型是最符合自然界随机概率分布的一种云模型，具有重要的数学意义。

设C是定量论域U上的定性概念，若定量值x∈U是定性概念C的一次随机实现,x对C的确定度u(x)∈[0, 1]是有稳定倾向的随机数，且隶属度函数满足下式：

(9)

则所有云滴x构成的随机变量X在论域U上的分布称为正态云模型。

云模型由期望Ex、熵En和超熵He三个数学参数表征。Ex是云滴在论域空间分布的期望值，是定性概念量化的典型样本；En是定性概念不确定性的度量，由概念的随机性和模糊性决定；He代表En的不确定性度量，由En的随机性和模糊性决定，描述了云滴的离散程度[17]。图2显示的是正态云模型中云滴的分布情况与数字特征值的关系，显而易见，云滴分布范围随En的增大而扩大，离散程度随He的增大而增大，很好地反映出云滴分布的随机性和模糊性。正态分布云滴的生成步骤如下：

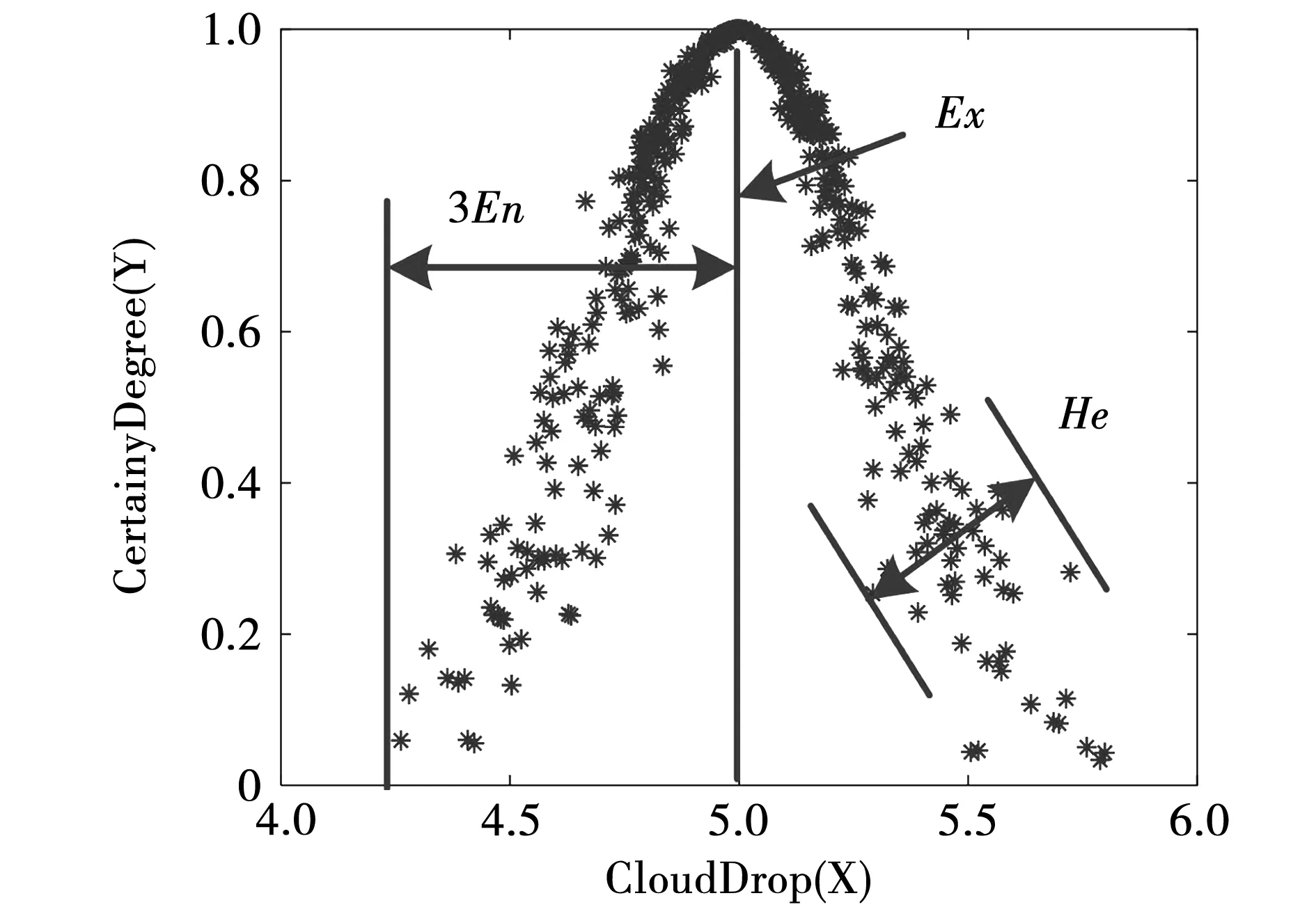
图2 正态云Fig.2 Normal cloud

(10)

式中En和He为云模型中的熵和超熵。

Step 2：生成正态分布随机数xi，公式为

(11)

式中Ex为期望。

Step 3：计算xi对应的确定度μ(xi)，隶属度函数如下：

(12)

令(xi,μ(xi))为一个云滴，则步骤Step 1～Step 3为产生服从正态分布云滴的步骤，定义为云生成器。云生成器根据设定的数字特征运行一次即产生一个云滴，直到运行生成期望数量的云滴。正态云滴生成过程可定义为如下形式：

X[x1,x2,…,xNd]=Gnc(Ex,En,He,Nd)。

(13)

2.3 CSSA

为了进一步改善SSA在解决多模态问题时跳出局部最优解的能力，在标准樽海鞘群算法的基础上引入正态云模型作为樽海鞘跟随者新的位置更新机制。新机制中在樽海鞘跟随者位置更新阶段，选择樽海鞘领导者所在的位置作为正态云模型的期望值Ex，则新的樽海鞘位置更新公式为

follower_SalpPositionj=GnC(leader_SalpPositionj,En,He,Nd)

(14)

式中：leader_SalpPositionj和follower_SalpPositionj分别表示第j维空间中樽海鞘领导者和追随者的位置；En和He的取值随着迭代数变化而自适应调整，En和He取值公式为：

(15)

He=En×10-ζ。

(16)

式中：ω∈(0,1)；τ、ζ为正整数；t为当前迭代次数；Tmax为最大迭代次数。

如上所述，CSSA算法描述如下：

Step 1：设置算法参数，并随机初始化樽海鞘

Step 2：计算樽海鞘个体的适应度Fitness，并对其进行排序，选出适应度最优个体的位置作为食物源F；

Step 3：由SSA中的式(5)对樽海鞘群领导者的位置进行更新；

Step 4：通过正态云模型即式(14)得到樽海鞘群追随者的位置；

Step 5：计算樽海鞘群更新后的个体适应度Fitness，通过比较得到的最优个体的位置作为新的食物源F；

Step 6：判断是否达到最大迭代次数Tmax，如果达到了则算法结束，输出食物源位置F，否则返回Step 3。

3 基于CSSA的PMSM参数辨识

对PMSM多参数的辨识，实际上是系统最优化问题。PMSM的辨识过程是根据辨识模型的输出与系统实际值经过适应度函数得到的适应值，通过优化算法对辨识模型中的待辨识参数进行不断修正，从而辨识出电机参数。CSSA不断筛选PMSM待辨识参数，使得辨识模型与实际值的适应度函数值达到最小，适应度函数值越小，其辨识模型的电压与实际值越接近，从而待辨识参数与实际值也越接近。适应度函数为

(17)

式中，h1、h2、h3和h4为适应度函数的权重系数,在适应度值相同的情况下，不同的权重分配会有不同的辨识精度。图3为基于CSSA的PMSM多参数辨识原理。

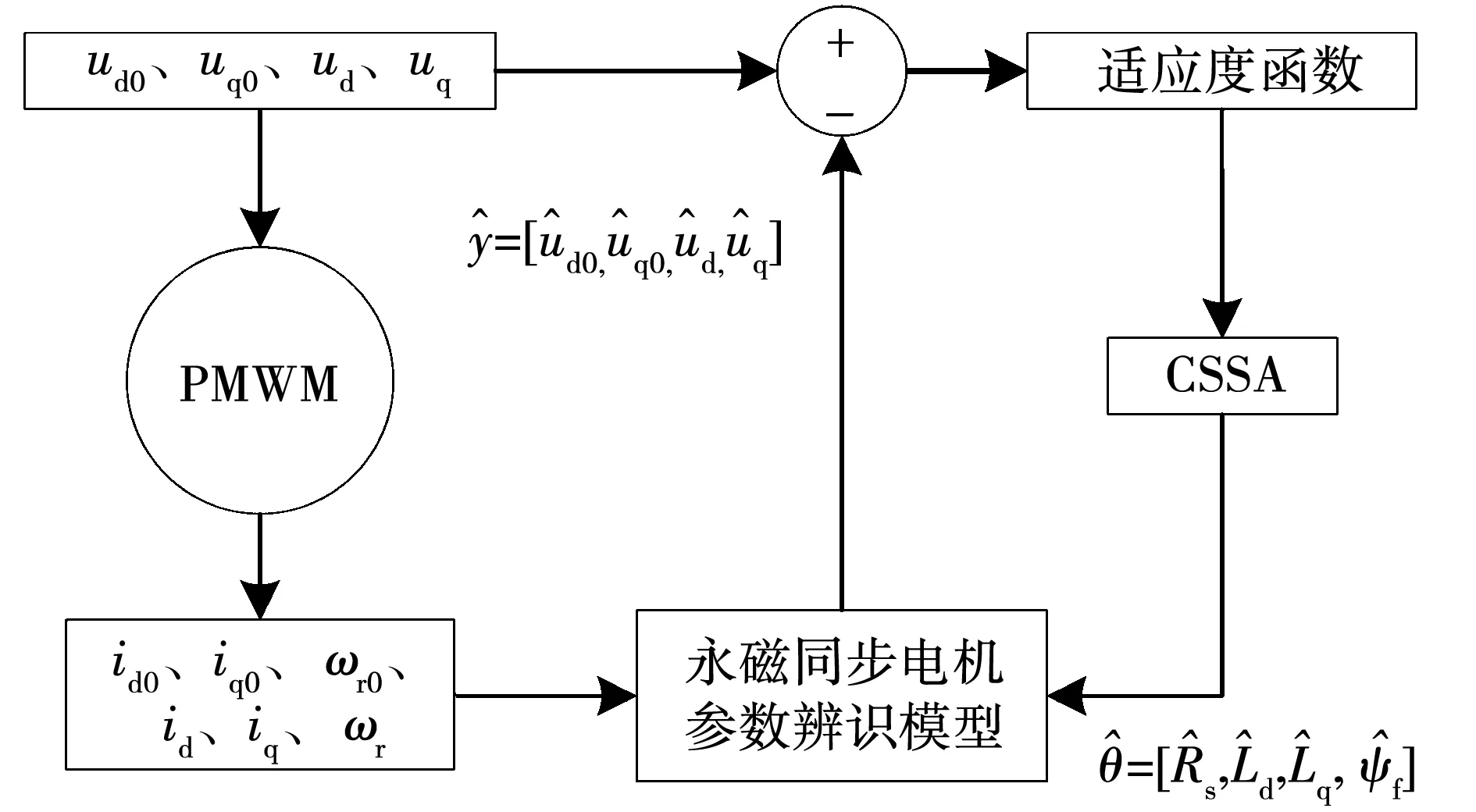
图3 基于CSSA的PMSM参数辨识原理图Fig.3 Principle diagram of PMSM parameters identification based on CSSA

4 仿真分析

本次仿真在MATLAB/Simulink软件平台上进行。仿真模型相对于实际电机而言有许多有优点：

1)电机参数值不会改变；

2)不受各种环境因素影响；

3)电气信号的采集不会受到影响。

因此仿真实验比实物实验能更好检验辨识优化算法的寻优能力。图4所示为PMSM矢量控制系统的仿真模型，在仿真电机稳定运行中采集电流、电压、电角速度的数据并保存到Matlab的工作区间，使用CSSA的m文件完成PMSM多参数的辨识。仿真电机的参数设置如表1所示。

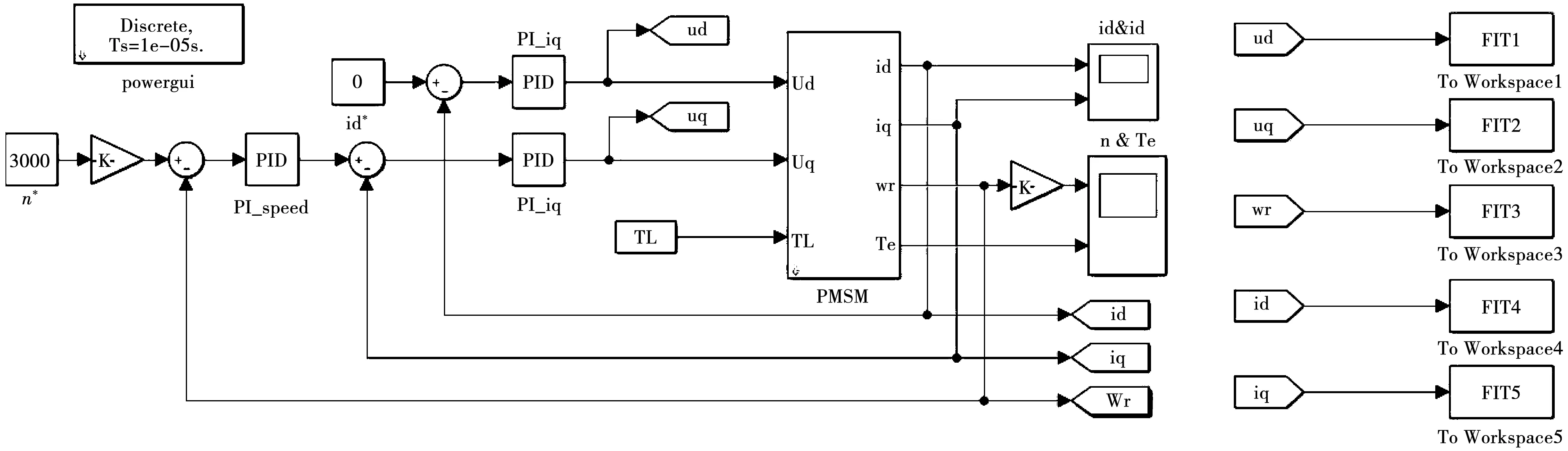
图4 PMSM矢量控制系统仿真模型Fig.4 Simulation model of PMSM vector control system

表1 PMSM参数Table 1 Parameters of PMSM

本次仿真采用了正态云模型樽海鞘群算法(CSSA)、增强型准海鞘群算法(ESSA)[18]、樽海鞘群算法(SSA)以及灰狼优化算法(GWO)[19]对PMSM参数进行辨识。仿真实验中，电机转速设置为3 000 r/min，负载转矩设置为5 N·m，在矢量控制id= 0和id=-0.5两种状态下分别都采集时长为50 ms的数据，共1 000组数据，并保存下来。为了确保仿真测试的合理性，四种算法的初始设置一致，种群规模都为30，最大迭代次数都为200次。为了检验算法的寻优能力，四个待辨识参数的范围都设置为[0，5]，远离电机参数的数值。为避免算法的随机性带来的辨识误差，每个算法的仿真实验独立运行15次，取其平均值作为最终输出值。

表2所示为四种算法的仿真结果，其中Mean为平均值、Err为误差、Std为标准差。通过对比可知，CSSA算法相对于ESSA、SSA和GWO算法的辨识效果最优，其适应度值最小，四个辨识参数值的误差最小，辨识的准确性高，同时标准差值也为最小，表示辨识过程的稳定性更好。

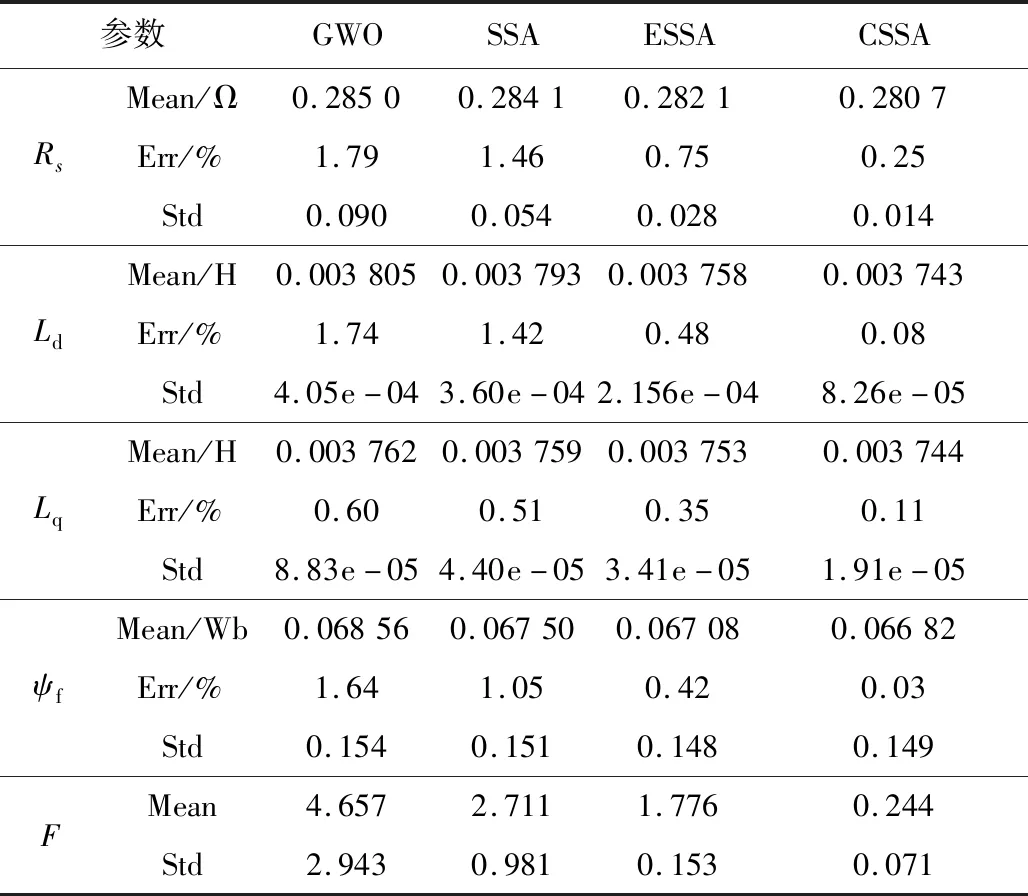
表2 四种算法仿真结果对比Table 2 Comparison of simulation results of four algorithms

5 实验与分析

5.1 实验平台与方案

为了进一步验证CSSA的有效性，搭建了PMSM参数辨识的实验平台，其构成如图5所示。实验平台采用了以DSP28035为核心的PMSM控制系统。在电机运行稳定后，采用图1所示的方法进行采样，采样数据经DSP控制器进行坐标转换后，通过CAN总线将数据传递给上位机，并完成参数辨识。实验中的所有参数设置，采样数据总数与仿真保持一致，同时为了避免辨识的偶然性，每个实验都独立运行15次，取其平均值作为输出结果。

图5 实验平台Fig.5 Experimental platform

5.2 实验结果与分析

图6所示为使用4种算法对PMSM进行参数辨识的平均适应度变化曲线，从图中可以看出，CSSA在迭代次数达到120次时收敛，收敛速度要优于其他三种算法；同时，从图中可知CSSA的适应度值最小，表明其寻优结果最优，参数辨识精度最高。

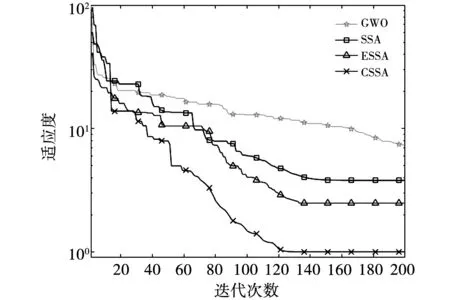
图6 平均适应度曲线Fig.6 Average fitness curve

图7～图10分别为PMSM各参数的辨识曲线，从图中的参数辨识曲线可知，4种算法均可以收敛到电机实际参数值附近，表明4种算法的全局搜索能力良好。同时，对比4种算法在接近电机实际参数值时所需的迭代次数，可以看到CSSA算法的收敛速度优于ESSA、SSA和GWO，且CSSA算法迭代过程中的波动最小，说明CSSA算法具有更好的稳定性。

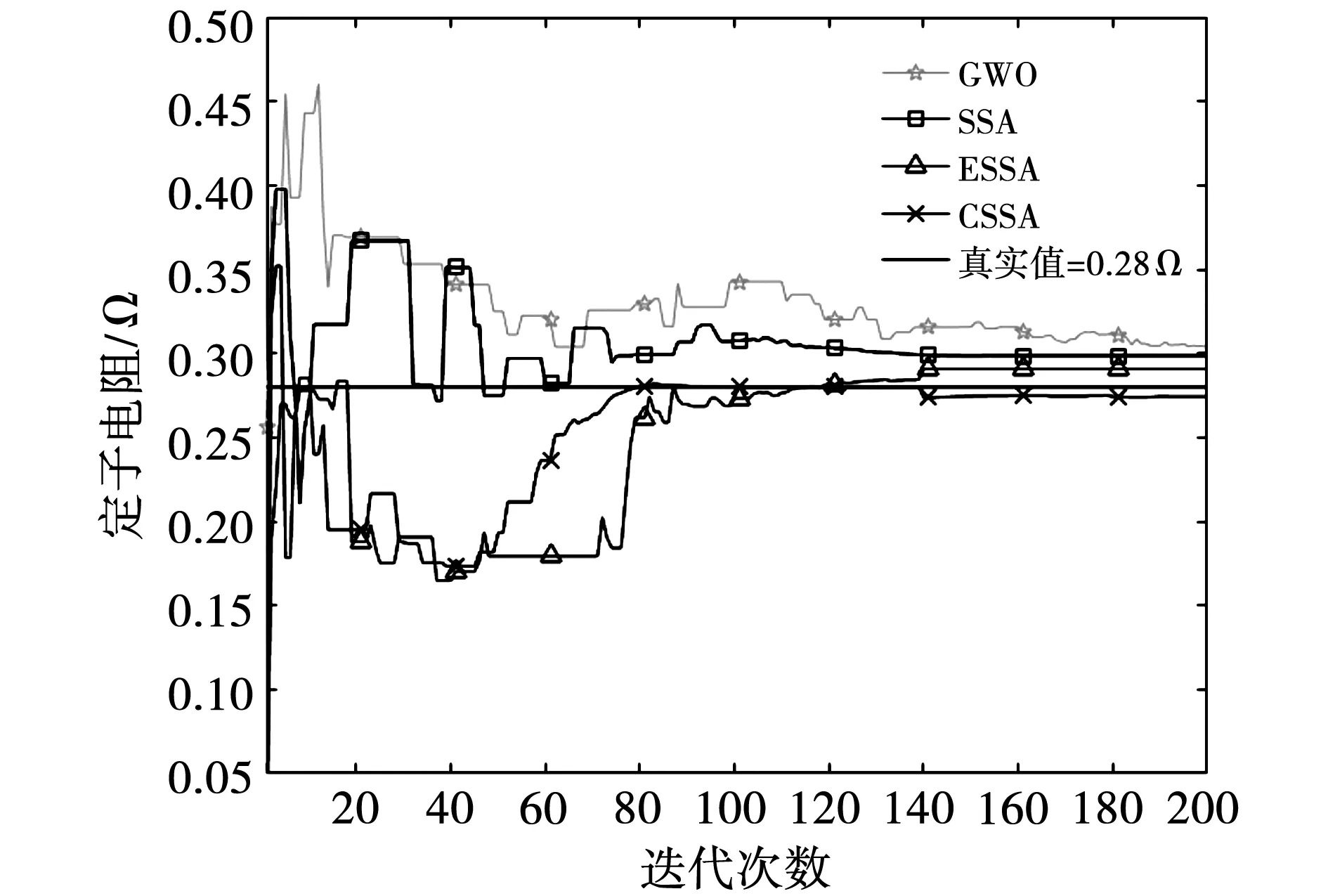
图7 定子电阻辨识曲线Fig.7 Identification curve of stator resistance

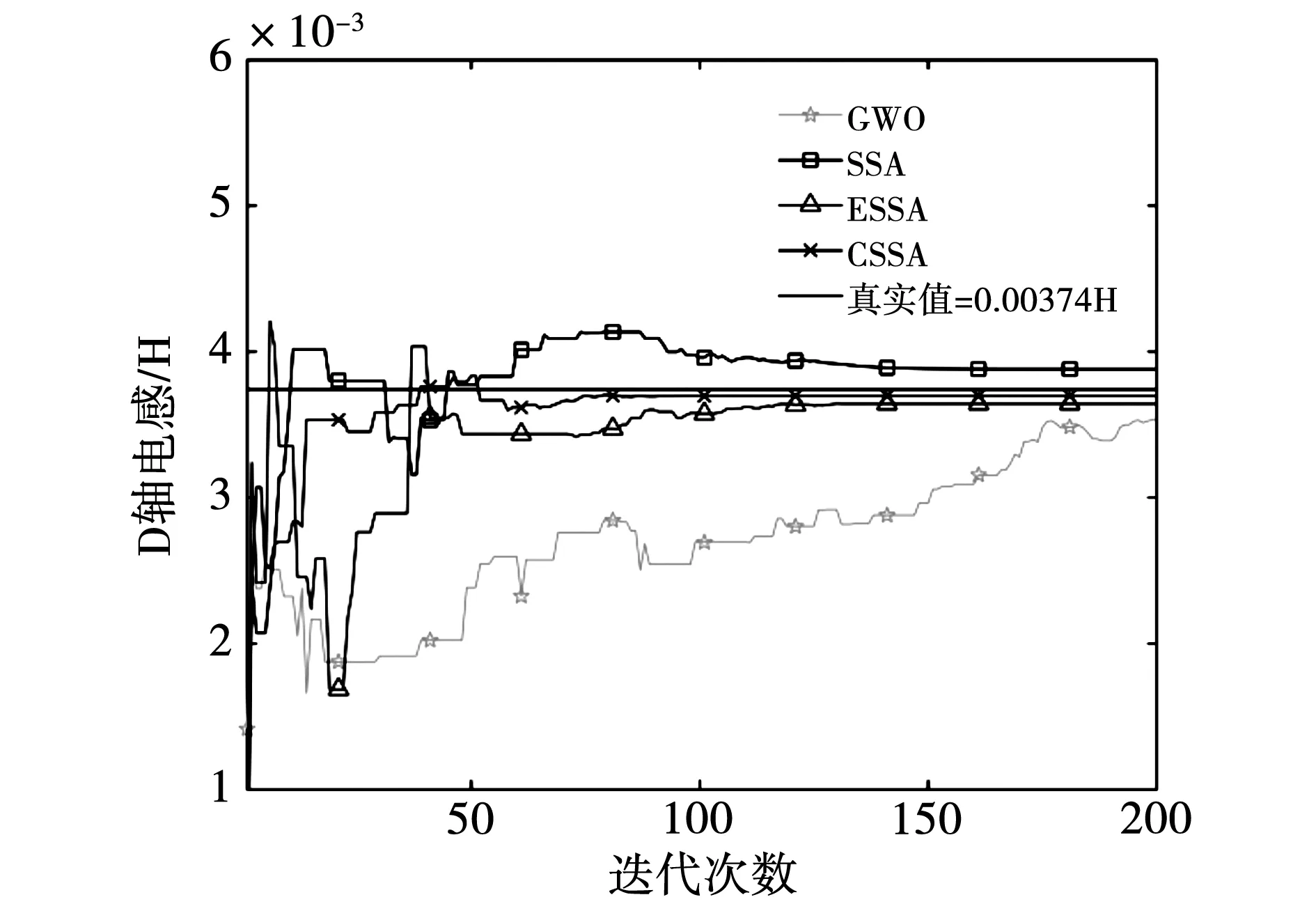
图8 d轴电感辨识曲线Fig.8 Identification curve of d-axis inductance

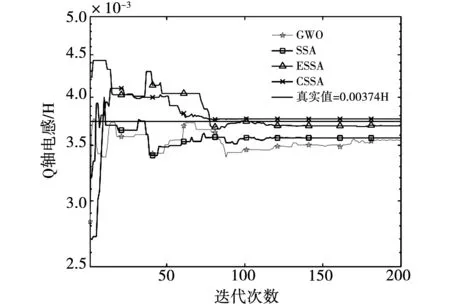
图9 q轴电感辨识曲线Fig.9 Identification curve of q-axis inductance

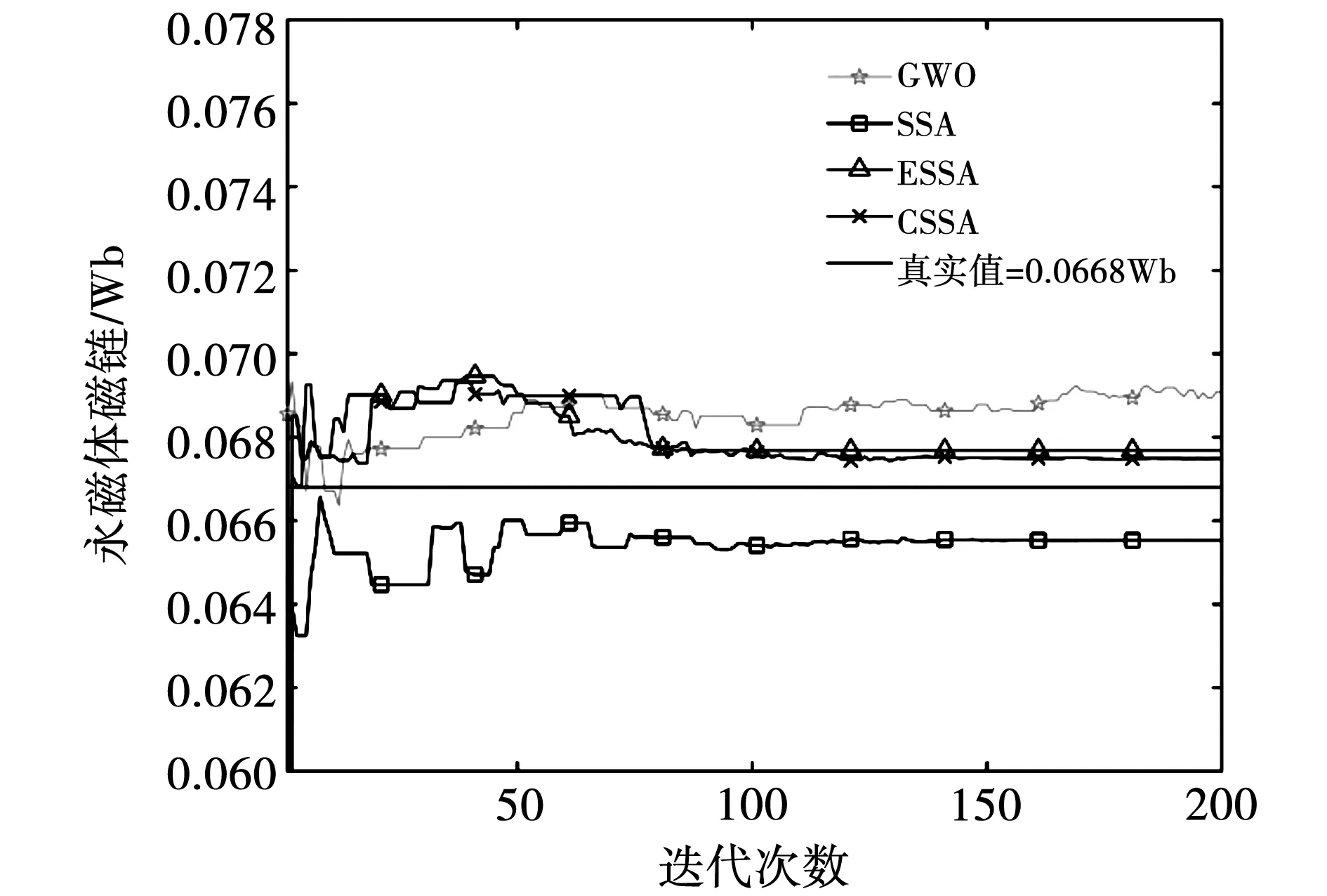
图10 永磁体磁链辨识曲线Fig.10 Identification curve of flux linkage

4种优化算法迭代到200次的辨识结果如表3所示。从实验结果可知，CSSA算法的适应度值最小，辨识值精度也最高，进一步验证了算法的有效性。在CSSA算法辨识的4个参数中，电感和磁链的波动较小，且辨识值也非常接近电机实际值，说明在辨识模型中，这三个参数的变化对适应度函数影响较大，而定子电阻的影响相对较小。

表3 四种算法实验结果对比Table 3 Comparison of experimental results of four algorithms

6 结 论

本文在PMSM的同步旋转dq坐标轴下，采用id=0的矢量控制和注入id≠0的负序弱磁电流两种控制策略构建一个满秩的参数辨识模型，运用基于自适应云模型的樽海鞘群算法能同时准确辨识定子电阻，d、q轴电感和永磁体磁链四个参数。该算法在标准樽海鞘群算法的基础，引入正态云模型，同时随着迭代次数增加，通过自适应调整正态云模型熵值，改进后的樽海鞘群算法在全局搜索和局部开发的能力得到较好提升。仿真和实验验证了在PMSM参数辨识中，CSSA算法相对于ESSA、SSA、GWO算法更加快速、准确和稳定。