一种正弦补偿型转矩分配函数的SRM转矩脉动抑制策略

2022-09-14贲彤聂恒陈龙王进井立兵

电机与控制学报 2022年8期

贲彤，聂恒，陈龙，王进，井立兵

(三峡大学电气与新能源学院，湖北宜昌 443002)

0 引言

由于开关磁阻电机(switched reluctance motor，SRM)具有结构简单、性能可靠、容错性高、成本低、调速范围广等优点，近些年在电气传动领域得到广泛应用，尤其SRM在电动汽车领域中用作驱动电机的广阔前景备受瞩目[1-5]。然而，SRM的双凸极结构和间歇电流激励导致转矩脉动和峰值电流过大，换相区间尤为显著，这限制了SRM的推广与应用[6-7]。

SRM转矩脉动控制方法包括：直接转矩控制(direct torque control,DTC)[8-9]、直接瞬时转矩控制(direct instantaneous torque control,DITC)[10-11]和转矩分配函数控制(torque sharing function,TSF)[12-13]等，其中TSF控制应用较为广泛。TSF是关于导通角、相电流重叠角的分段函数，导通角、重叠角等参数对TSF的波形有显著影响[14-15]。

对传统TSF进行改进，可实现电机性能的优化。其中，低电流跟踪误差型TSF通过考虑电流动态特性，可降低TSF的电流跟踪误差，抑制转矩脉动和峰值电流，但是该方法会产生负转矩，使SRM的效率降低[16]。转矩反馈型TSF通过相邻两相的期望转矩与实时转矩差值，反馈到给定转矩，补偿该相跌落的转矩，可减小SRM换相区间的转矩脉动，但是该方法使峰值电流增加，没有考虑电机铜损耗[17]。二次补偿型TSF采用遗传算法，以SRM的实时电流变化率和铜损耗为优化目标，对直线型TSF进行二次型曲线补偿，整体抑制了转矩脉动和峰值电流，但在换相区间的转矩脉动和峰值电流较大[18]。在线补偿型TSF针对不同换相区间，对转矩分配函数进行在线正补偿或负补偿，实现换相阶段总转矩脉动抑制，但未考虑峰值电流对电机铜损耗的影响[19]。模糊逻辑控制型TSF将TSF与模糊逻辑控制结合，可以对转矩脉动抑制，但增大了换相区间的峰值电流，导致电机的铜损耗增加，效率降低[20]。综上，目前改进型TSF存在转矩脉动抑制和降低铜损耗无法兼顾，且难以同时保证换相区间转矩脉动和峰值电流跃变的问题。

针对上述问题，本文提出一种正弦补偿型TSF，并利用NSGA-II算法的全局寻优能力，以转矩脉动和铜损耗为优化目标，对正弦补偿型TSF参数进行多目标寻优，通过对比不同转速、不同负载下的电流和输出转矩波形，可知该方法可同时保证转矩脉动抑制，峰值电流减小，换相区间转矩脉动和峰值电流不发生跃变。通过实验验证正弦补偿型TSF在SRM换相区间同时抑制转矩脉动和峰值电流的性能。

1 SRM非线性模型的建立

由于SRM的双凸极结构和开关控制方式，且SRM的电感-电流-位置和转矩特性曲线均为非线性，因此，为了获得上述非线性特性曲线，需建立SRM的非线性模型。本文结合有限元分析方法与控制模块，对一台三相12/8极SRM进行电磁和转矩特性计算，电机参数如表1所示。

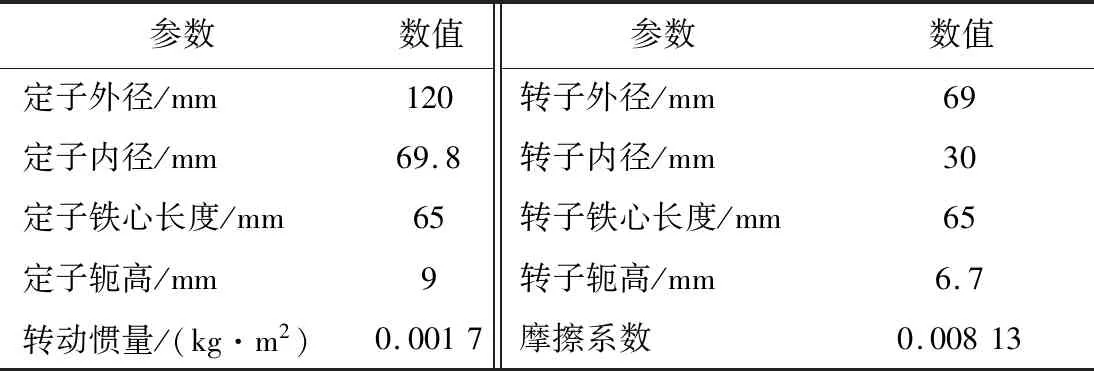
表1 开关磁阻电机模型主要参数Table 1 Main parameters of SRM model

1.1 考虑磁化非线性的SRM有限元模型

SRM电感-电流-位置和转矩特性曲线表现为非线性的根本原因是定转子铁心工作在材料磁化特性的非线性区，因此，在电机的有限元模型中，采用实测的B-H曲线，如图1所示，测试样片为牌号50WW470的无取向硅钢，即电机定转子叠片材料。

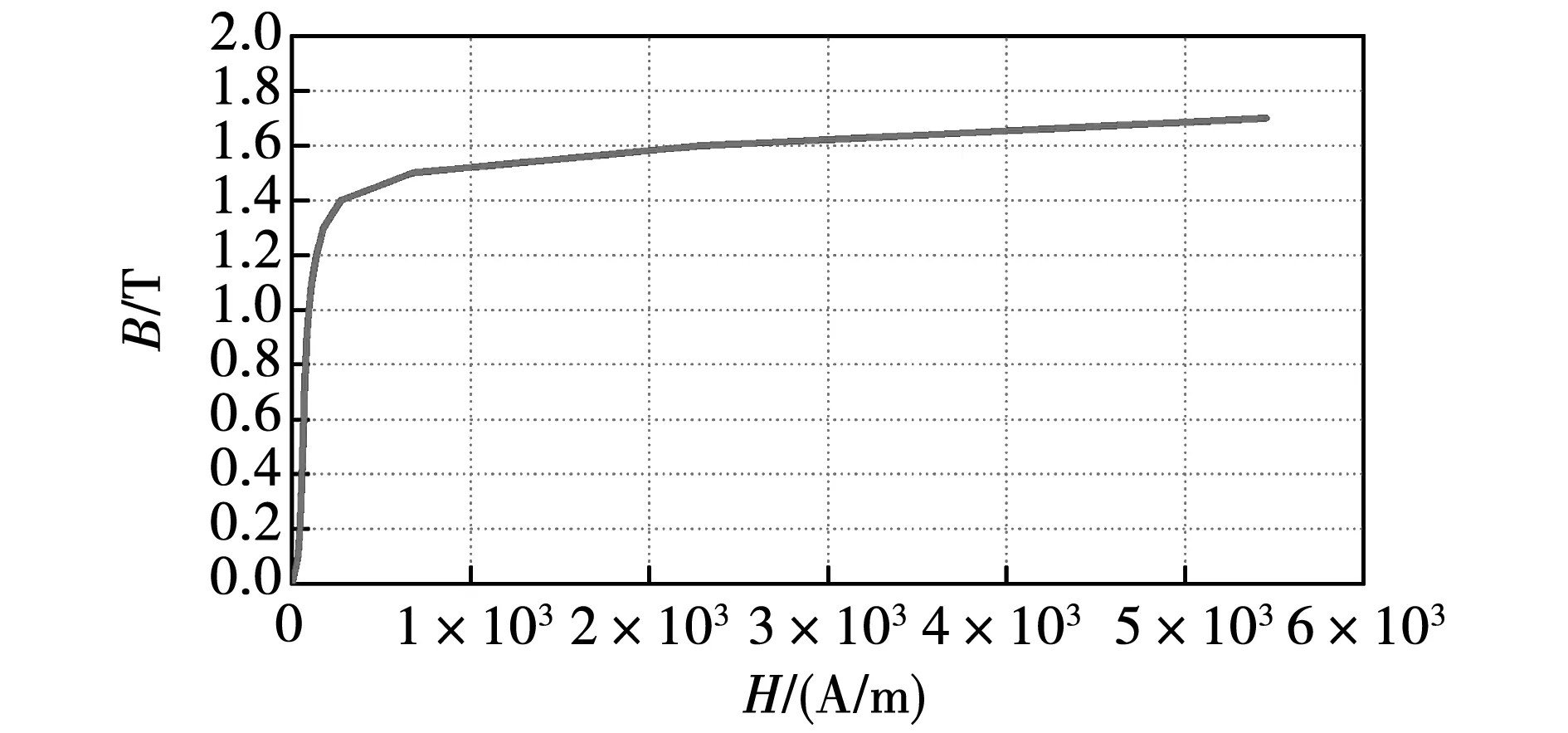
图1 硅钢片的B-H曲线Fig.1 B-H curve of silicon steel sheet

SRM定转子不同位置的磁通密度分布如图2所示，其中：0°是转子槽中心与定子齿中心对齐的位置，即不对齐位置；22.5°是转子齿中心与定子齿中心对齐的位置，即对齐位置。在0°时，磁阻最大，SRM漏磁最为严重；随着转子由0°位置向22.5°位置转动，转子齿与定子齿重合范围增加，漏磁减少，磁密增大，在SRM定转子齿尖易产生局部饱和现象；在22.5°时，磁阻最小，漏磁最小。

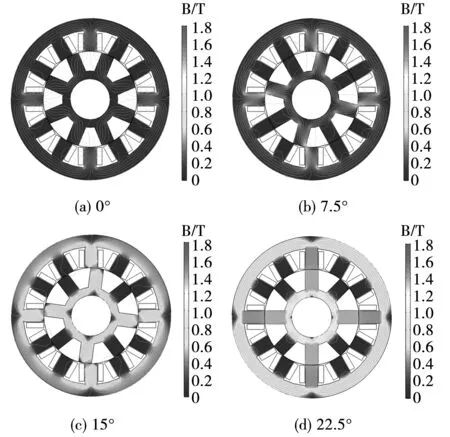
图2 SRM的磁通密度分布图Fig.2 Flux density distribution of SRM

根据电机磁通密度可获得磁链特性曲线，表达式为

(1)

式中：B为磁通密度；S为绕组的横截面积，其值为1.057 mm2；N为绕组的匝数，其值为50。

SRM的磁链特性曲线如图3所示，由图3(a)可知，当SRM定转子处于靠近不对齐位置(即0°)时，绕组的磁链较小，随着电流增大，磁链随之增大，当到达靠近对齐位置(即22.5°)时，磁链最大。由图3(b)可知，当SRM电流激励较小(1 A)时，磁链随着转子向对齐位置转动而增大，此时磁链特性接近线性；随着电流的增大，磁链随之增大，但其增量随电流的增大而减小，说明磁路出现非线性饱和特性。

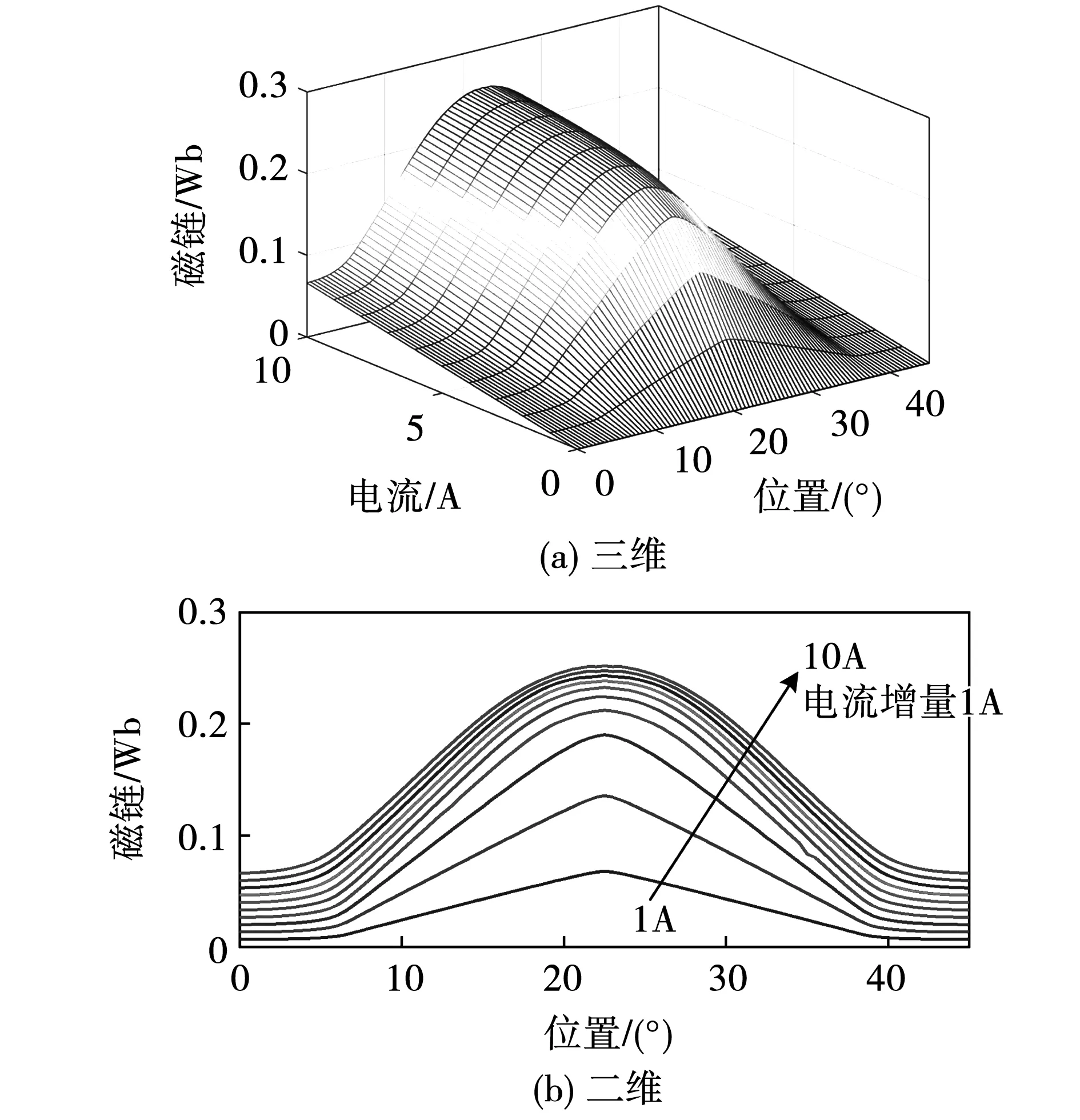
图3 磁链特性曲线Fig.3 Flux linkage characteristic curve

由于线性模型中磁链会随电流增加而无限增大，这与电机实际工作状态不符，会导致控制算法无法精确预判SRM的瞬时转矩，直接影响系统的驱动效率和转矩脉动抑制效果；而本文提出的考虑磁化非线性的SRM有限元模型可准确模拟电机铁心磁路的非线性饱和特性，因此，可实现对SRM在饱和区域的精确控制。

SRM相绕组的磁链ψk是关于相电流ik和转子位置角θ的函数，其表达式为

ψk(θ,ik)=Lk(θ,ik)ik。

(2)

式中：ik和Lk分别是SRM第k相绕组的电流电感值；θ为转子位置角。

根据已获得的磁链特性曲线以及式(2)可以得到SRM第k相绕组的静态电感特性曲线，如图4所示。在不对齐位置(即0°)，电感值不随着电流激励的变化而变化；在对齐位置(即22.5°)，电感值随电流的增大而减小。随着电流激励的增大，电感值随转子位置的变化率呈非线性减小，即出现了饱和非线性特性。

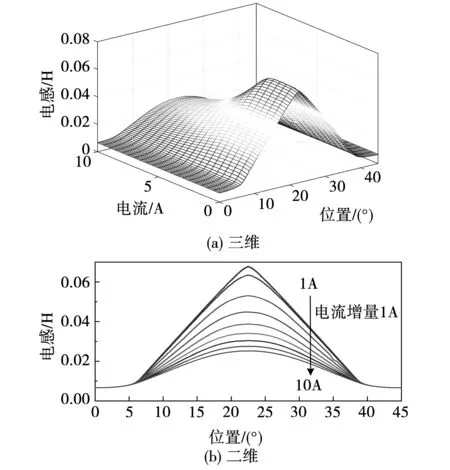
图4 静态电感特性Fig.4 Static inductance characteristics

根据机电能量转换原理，转矩可由磁共能W′(θ,ik)对θ求偏导得到，其表达式为

(3)

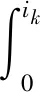
(4)

式中Tk为第k相绕组产生的转矩。

根据已获得的磁链特性曲线以及式(3)、式(4)可得SRM第k相绕组的静态转矩特性曲线，如图5所示。由图可知：在对齐位置(即0°)和不对齐位置(即22.5°)，转矩均为0，在中间位置，SRM的转矩最大，其正负与电感随转子位置角变化相关，在电感上升区间，提供正转矩，在电感下降区间，提供负转矩，且转矩随电流的增加而非线性增大。

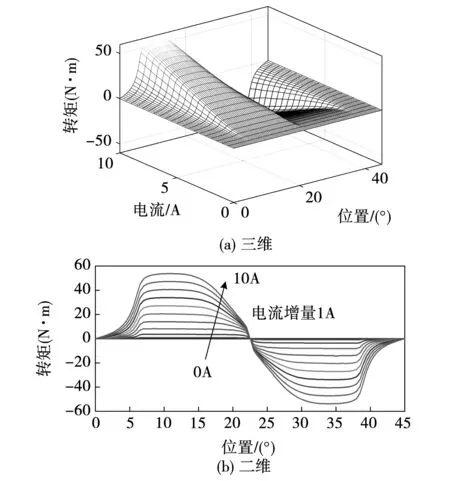
图5 静态转矩特性Fig.5 Static torque characteristics

1.2 SRM非线性绕组模型

根据上述有限元分析结果，建立SRM静态电感特性Lk(θ，i)和静态转矩特性Tk(θ，i)的非线性数据，将其预存至查表模块，分别得到考虑非线性的电感模块和转矩模块。

SRM的第k相绕组的电压平衡方程为

(5)

式中uk和Rk分别为SRM第k相绕组的电压和电阻。

SRM的转子机械方程为

(6)

式中：Te为电磁转矩；TL为负载转矩；J为转动惯量；D为摩擦系数。

根据电压平衡方程和转子机械方程，搭建SRM非线性控制模型，其中，式(5)中的电感Lk为非线性的电感模块，式(6)中的电磁转矩Te为A、B、C三相非线性的转矩模块输出的和，即Te=TA+TB+TC。

根据式(5)，可得到第k相绕组的电流表达式

(7)

根据式(7)搭建的A相绕组的模型如图6所示，B、C两相与A相绕组模型相同，相邻相之间间隔30°即可。图6中，A+、A-是SRM功率变换器在A相的两个开关管施加在A相绕组上的激励电压uA，电压测量V输出的是uA-RAiA。非线性电感模块Lk(θ，i)和非线性转矩模块Tk(θ，i)利用Look-up Table(2-D)建模，根据输入的转子位置角θ和相电流iA分别输出A相绕组当前的电感值Lk和提供的转矩值Tk。该模型考虑了电感特性和转矩特性的非线性，通过转子位置θ和激励电压ua可以获得A相绕组当前提供的转矩值TA和相电流值iA。

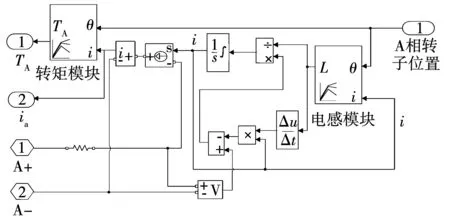
图6 SRM的A相绕组模型Fig.6 Phase A winding model of SRM

2 转矩分配函数控制策略

2.1 直线型TSF

TSF控制是根据转子所在的位置角，通过分段函数将合成转矩分配给各相，各相跟踪各自的相指令转矩，使瞬时的合成转矩为恒定值，以实现抑制转矩脉动的目的。

定义fk(θ)为第k相转矩的分配函数，则有

(8)

式中：Tk(θ)为第k相的瞬时转矩；Tref为瞬时的合成转矩指令值；m为SRM的相数。

经典的TSF控制方式有直线型、指数型、正弦型和立方型等四种，其中直线型的分配函数表达式为：

(9)

式中：θon、θov、θoff分别为导通角、相邻两相电流重叠角以及关断角；τ为SRM的一个转子角周期，可表示为τ=2π/Nr，其中Nr为SRM转子极数。

直线型TSF波形如图7所示，fA(θ)、fB(θ)、fC(θ)分别为A、B、C三相各相的转矩分配函数。由于SRM的电感特性和转矩特性都有很强的非线性，直线型TSF对转矩进行线性分配，在换相区间(即图中θov区域)，关断相提供的转矩开始减小，而导通相又不足以提供足够的转矩时，这就导致使用直线型TSF控制时，其实际值与给定值之间误差增大，造成较大的转矩脉动和峰值电流。

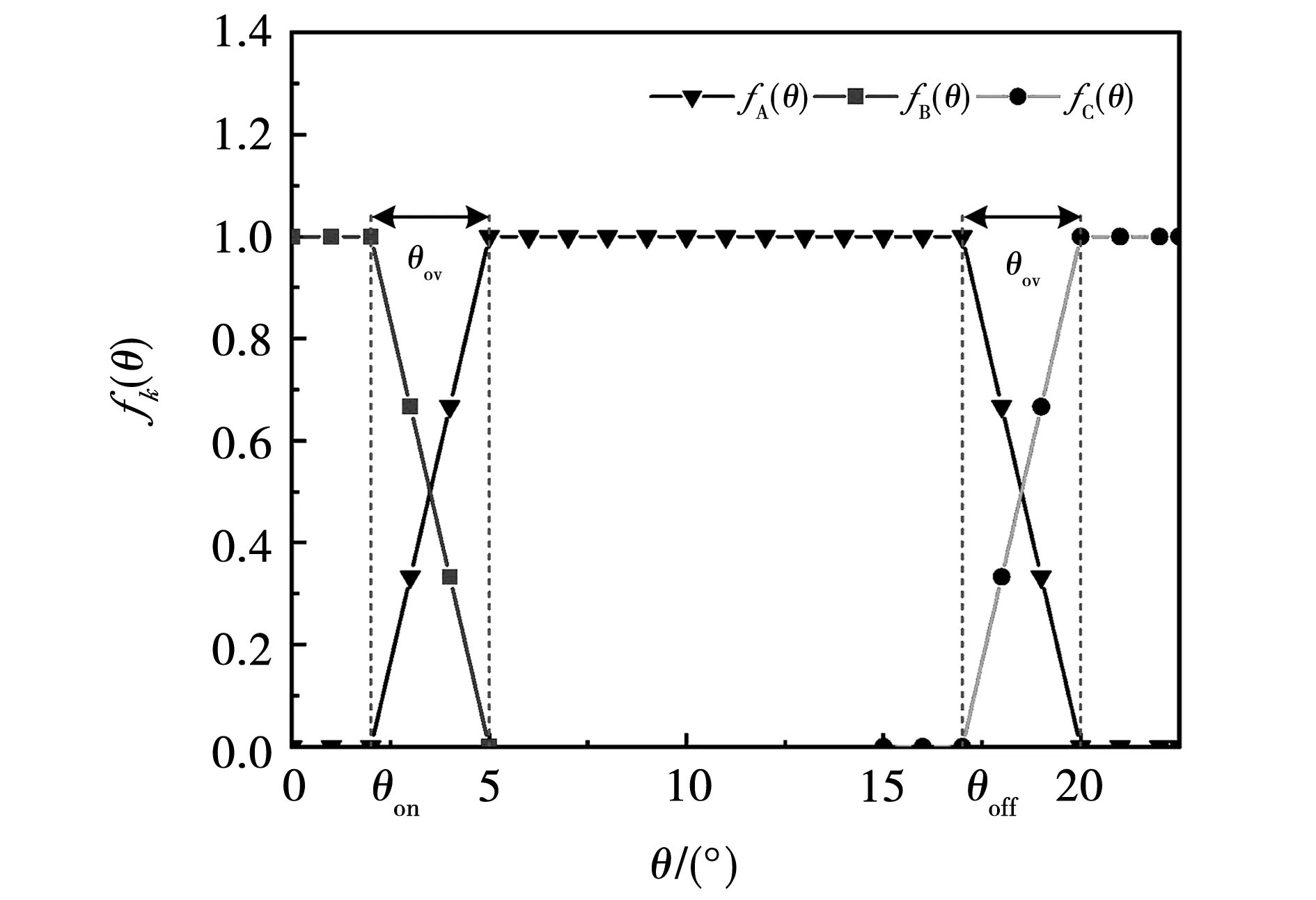
图7 直线型TSF波形Fig.7 Linear TSF waveform

2.2 正弦补偿型TSF

为了降低换相区间的峰值电流和转矩脉动，本文提出一种正弦补偿型TSF，其设计原则为：一是各相只产生正的电磁转矩，不产生负的电磁转矩；二是不管在任何时刻，只有一相或者相邻的两相绕组导通。据此，在直线型TSF的换相区间增加正弦补偿曲线，增大TSF在换相区间的平滑性，正弦补偿曲线的表达式为

(10)

式中：c1、c2分别为TSF上升和下降过程中的正弦补偿曲线函数；n为常数。

正弦补偿型TSF可以表示为：

(11)

据此，可得到正弦补偿型TSF波形，如图8所示，其中：fk*(θ)为正弦补偿型TSF第k相转矩的分配函数；θstep为步进角，表示为

θstep=2π/mNr。

(12)

式中：m为SRM相数；Nr为SRM转子极数。

由图8和式(10)、式(11)可知，正弦补偿型TSF是在直线型TSF换相区间内增加了一个周期为θov的正弦补偿曲线。由图8(b)可知，正弦补偿型TSF在换相区间前半段给导通相分配了更小的转矩，在换相区间后半段给导通相分配更大的转矩，这使补偿后的TSF曲线更加平滑，可减小转矩脉动。

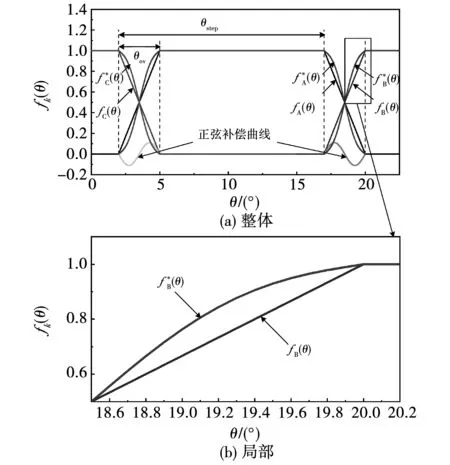
图8 正弦补偿型TSF波形Fig.8 Sinusoidal compensated TSF waveform

3 NSGA-II全局参数优化

SRM在不同转速下，其控制策略的参数取值不同，且在控制转矩脉动最小的同时，还应使电机的铜损耗最小，这样才能实现电机的节能降耗；同时，重叠角θov、导通角θon对TSF控制适用的转速范围、最高转速以及SRM的效率等影响显著，且系数n所决定的正弦补偿曲线波形也直接影响TSF性能。因此，需对不同转速下正弦补偿型TSF的导通角θon、重叠角θov以及系数n进行优化。

对于上述多目标优化问题，各个目标之间存在相互制约的关系，一个目标实现最优是以损失其他目标性能为代价，即不可能存在一个最优解使得所有目标性能都得到改善，因此，对于多目标优化问题，其解是一个非劣解的集合-帕累托(Pareto)解集，多目标优化算法的目的就是要寻找这些Pareto最优解。

NSGA-II作为目前应用最为广泛的多目标优化算法之一，在解决SRM多目标优化问题中具有优越性，通过全局搜索重叠角θov、导通角θon以及系数n的数值组合，获得与该数值组合相对应的转矩脉动Tripple和均方根电流Irms最小化。因此，本文选择NSGA-II作为优化正弦补偿型TSF的算法。

3.1 目标函数和约束条件

本文将转矩脉动和铜损耗同时作为优化目标，为了方便计算，定义转矩脉动和铜损耗的两个性能指标Tripple和Irms来评价TSF的控制效果。

定义转矩脉动性能指标用瞬时转矩的均方根值Tripple来评价，表达式为

(13)

式中T、TL分别为瞬时实际转矩和负载转矩值。

定义铜损耗性能指标用均方根电流Irms来评价，表达式为

(14)

式中：ik为第k相的导通相电流；ik-1为第k-1相的导通相电流。

式(13)、式(14)中，t是仿真时长，为了分析SRM换相区间的转矩脉动和峰值电流的情况，仿真时长至少包含一次换相过程，即t必须大于SRM一相导通的时长(600 r/min时为1/30 s)，因此，本文取t=0.1 s。

由于本文主要解决传统的TSF存在换相区间转矩脉动和峰值电流较大的问题，因此，对换相区间的TSF进行了正弦补偿，根据图8正弦补偿型TSF的波形，可以得到

(15)

式中：θstep为15°；τ为45°，可知θov最大取值为7.5°，即SRM单相导通时间最短为7.5°。

当θov取0°时，单相导通时间取最短的7.5°时，可以得到θon的约束条件，公式如下：

(16)

为了保证SRM不产生负转矩，系数n要求不小于4，且系数n太大又会失去补偿效果，系数n要求不大于10。因此，优化变量的约束条件为：

(17)

3.2 全局优化过程及结果

本文采用NSGA-II为外部循环优化算法，并将正弦补偿型TSF控制下的转矩脉动和铜损耗作为优化目标，得到当前转速与参考转矩下最优的重叠角θov、导通角θon以及系数n。

基于NSGA-II优化的正弦补偿型TSF具体优化流程图如图9所示。首先，初始化种群，将重叠角θov、导通角θon以及系数n通过变量赋值的方式对SRM系统仿真模型中的相应模块赋值并运行；其次，将SRM系统仿真模型输出转换成标量，并调用到NSGA-II程序中对其评估；再次，进行种群的交叉、变异、合并以及生成新的种群；最后，新的种群被赋值到SRM系统仿真模型中的相应模块并计算，获得Pareto解集。

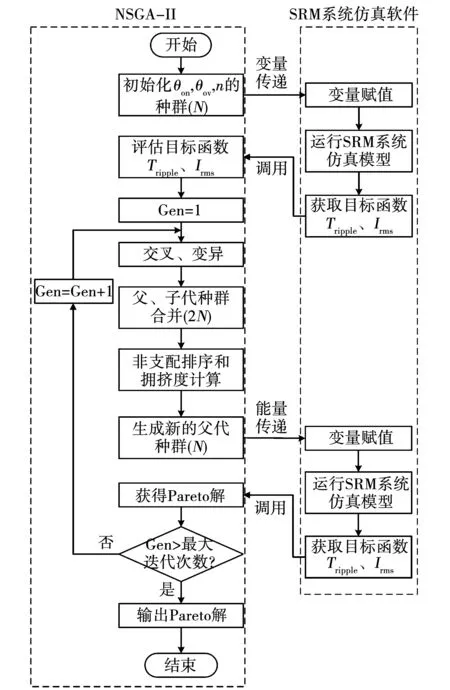
图9 NSGA-II优化具体流程图Fig.9 Optimize specific flow chart of NSGA-II

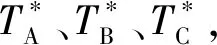
图10 SRM整体控制策略框图Fig.10 Overall control strategy block diagram of SRM

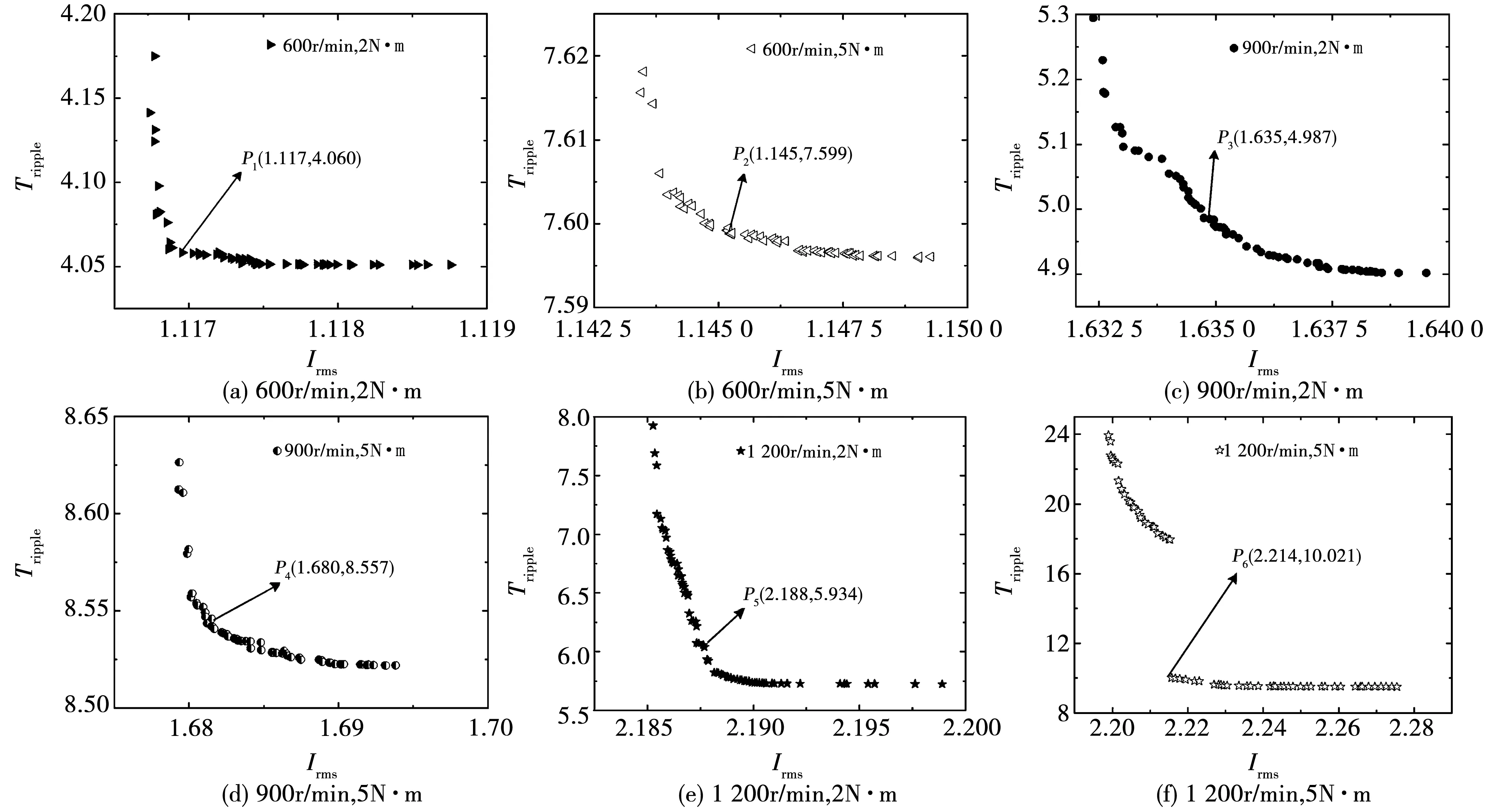
图11 不同转速、不同负载时的Pareto解集Fig.11 Pareto solution setunder different speeds and loads

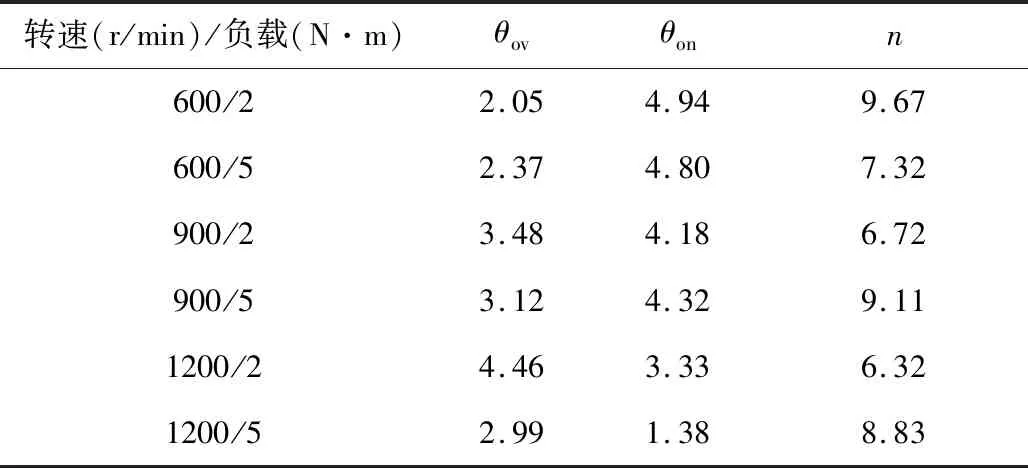
表2 正弦补偿型TSF最优参数Table 2 Optimal parameters of the sinusoidal compensated TSF

4 仿真结果与分析

为了验证本正弦补偿型TSF对SRM换相区间转矩脉动和峰值电流的抑制效果，以一台三相12/8极的SRM为研究对象，分别建立正弦补偿型TSF和直线型TSF两种系统仿真模型，负载转矩分别为2 N·m和5 N·m，转速分别为600、900和1 200 r/min。其中，正弦补偿型TSF控制参数为表3中得到的最优重叠角θov、导通角θon以及系数n。

4.1 正弦补偿型TSF与直线型TSF对比

负载转矩为2 N·m和5 N·m时的仿真结果分别如图12、图13所示，分析得到以下结论。

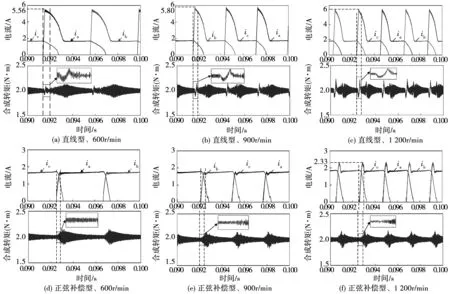
图12 负载为2 N·m时，不同转速下SRM的电流波形与合成转矩波形图Fig.12 Current waveform and synthetic torque waveform of SRM at different speeds when the load is 2 N·m

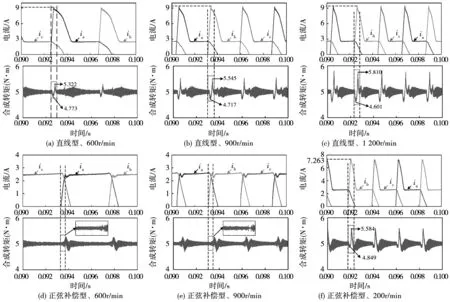
图13 负载为5 N·m时，不同转速下SRM的电流波形与合成转矩波形图Fig.13 Current waveform and synthetic torque waveform of SRM at different speeds when the load is 5 N·m

首先，对比转速为600 r/min、负载转矩为2 N·m时，两种控制方式下SRM的电流波形和合成转矩波形，如图12(a)、(d)所示，结果表明，低转速时，直线型TSF控制方法下换相区间的转矩脉动较大，且存在较大峰值电流，而正弦补偿型TSF控制方法在换相区间的转矩脉动较小，且峰值电流相对小3.825 3 A，减小了68.78%。

其次，对比转速为900 r/min、负载转矩为2 N·m时，两种控制方式下SRM的电流波形和合成转矩波形，如图12(b)、(e)所示，结果表明，中等转速时，直线型TSF控制方法下峰值电流和换相区间的转矩脉动比低转速时增大，而正弦补偿型TSF控制方法下峰值电流和换相区间的转矩脉动依然被控制得很小，说明正弦补偿型TSF在中低转速下能稳定的抑制换相区间的转矩脉动和峰值电流。

再次，对比转速为1 200 r/min、负载转矩为2 N·m时，两种控制方式下SRM的电流波形和合成转矩波形，如图12(c)、(f)所示，结果表明，高转速时，直线型TSF控制方法峰值电流和换相区间的转矩脉动持续增大，而正弦补偿型TSF控制方法下峰值电流虽然有所增大，但相对较小，换相区间的转矩脉动也依然控制得很小。同时，随着转速增大，正弦补偿型TSF的电流波形在换相区间也出现了较小尖峰(图12(f))，但峰值较小，为2.33 A，与直线型TSF的峰值电流为(6.02 A)相比，降低了61.29%。因此，正弦补偿型TSF在高转速下仍能稳定的抑制换相区间的转矩脉动和峰值电流。

最后，对比不同负载对电流波形和合成转矩的影响，结果表明：转矩脉动与负载的增加呈正相关，在转速一定的情况下，随着负载增加转矩脉动加剧；中低转速时，负载的增大使直线型TSF控制方法下的峰值电流和转矩脉动出现明显增大，而正弦补偿型TSF控制方法在大负载下，换相区间仍能保持较小的转矩脉动和峰值电流；高转速时，负载的增大使正弦补偿型TSF控制方法下的峰值电流增大到7.263 A，相比直线型TSF的峰值电流(9.433A)降低了23%，转矩脉动在换相区间出现较小尖峰(图13(f))，但峰值相对较小。因此，正弦补偿型TSF在高负载下仍能有效抑制换相区间的转矩脉动和峰值电流。

采用均方根电流Irms评价SRM的铜损耗(见公式(14))，为了定量分析两种TSF抑制SRM转矩脉动的性能，定义k为换相区间的转矩脉动率，其表达式为

(18)

式中Tmax、Tmin分别是换相区间瞬时合成转矩的最大值、最小值。

据此，得到直线型TSF与正弦补偿型TSF在不同转速、负载下的控制效果对比，如表3所示。由表可知：负载为2 N·m时，正弦补偿型TSF相比于直线型TSF，其转矩脉动率最高可降低62.29%，铜损耗最高可降低42.6%；随着负载的增大，正弦补偿型TSF的转矩脉动率和铜损耗最高可分别降低54.79%和42.41%。因此，正弦补偿型TSF在不同转速、负载下对换相区间的转矩脉动和铜损耗均有较好的抑制效果。

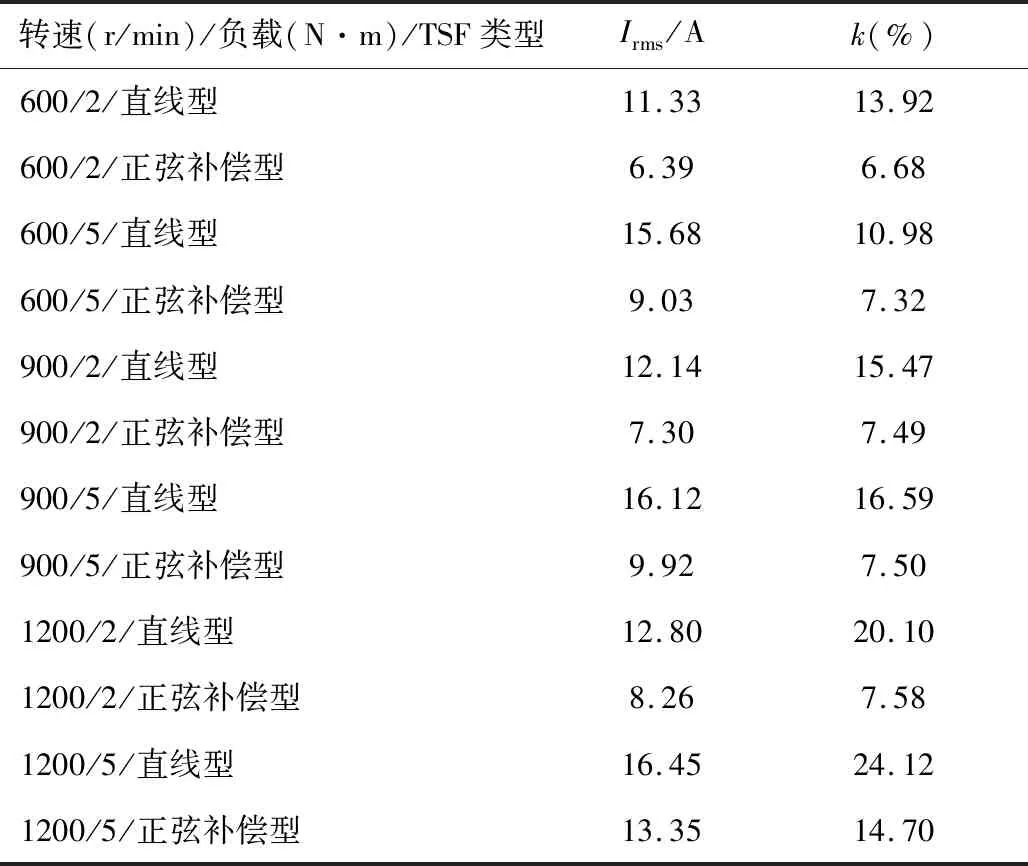
表3 直线型TSF与正弦补偿型TSF性能对比Table 3 Performance comparison of the linear TSF and the sinusoidal compensated TSF

4.2 正弦补偿型TSF与改进型TSF对比

为了进一步验证本文提出的正弦补偿型TSF对SRM转矩脉动和铜损耗的抑制效果，将正弦补偿型TSF与转矩反馈型、二次补偿型、在线补偿型三种改进型TSF方法进行对比，如表4所示，其中，对比参数为：

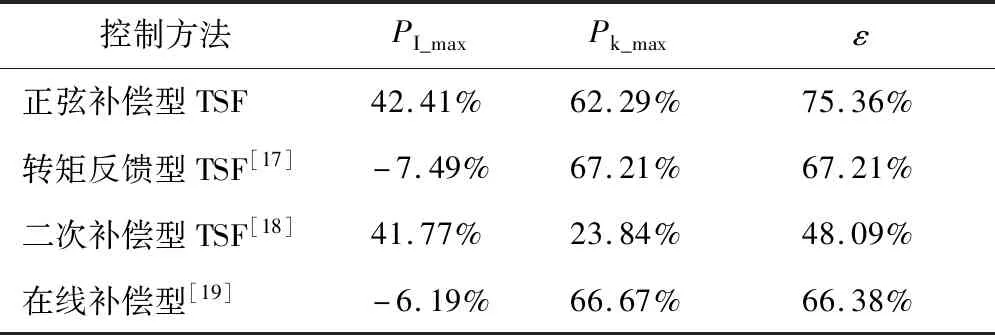
表4 正弦补偿型TSF与不同改进型TSF的性能对比Table 4 Performance comparison of the sinusoidal compensated TSF and different improved methods

1)PI为改进前后均方根电流Irms的降低比例，

(19)

式中I0、I1分别为改进前后的均方根电流。

2)Pk为换相区间转矩脉动率k的降低比例，

(20)

式中k0、k1分别为改进前后换相区间转矩脉动率。

3)ε为同时兼顾转矩脉动和铜损耗的综合性能参数，表示为

(21)

式中：PI_max和Pk_max分别为不同转速和负载下PI和Pk的最大值；当PI_max和Pk_max同号时，根号内取“+”；当PI_max和Pk_max异号时，根号内取“-”。

由表4可知，正弦补偿型TSF的PI_max均大于其他三种改进型TSF，其Pk_max值虽略小于转矩反馈型TSF和在线补偿型TSF，但相差不大，且ε值均大于其他三种改进型TSF。因此，本文提出的正弦补偿型TSF在转矩脉动抑制的同时，还能有效降低电机的铜损耗，提升电机效率，综合性能较高。

5 实验结果与分析

本文搭建了SRM实验平台，如图14所示。实验样机与仿真样机参数保持一致，其中：转矩信号由JN338型转矩传感器测量，其满量程频率输出为5～15 kHz；选用0～25 N·m规格的磁粉制动器作为实验负载，其大小由张力控制器调节；电流信号由Keysight Technologies的N2782B型电流探头测量；使用NI PXIe-6124多功能采集卡测量转矩和电流信号。测量SRM在传统方法控制下，负载转矩为2 N·m，转速为1 200 r/min的单相导通电流和合成转矩信号，与正弦补偿型TSF的单相导通电流和合成转矩波形对比如图15所示。

图14 SRM实验平台Fig.14 Experimental platform of SRM

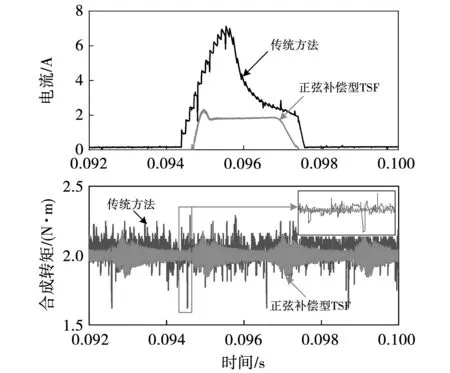
图15 传统方法与正弦补偿型TSF性能波形对比Fig.15 Performance waveform comparison between traditional method and sinusoidal compensation TSF

由图15可知，传统方法下，SRM在换相区间的电流峰值为7.125 A，正弦补偿型TSF的峰值电流为2.33 A，在该区间降低了67.29%；传统方法在换相区间转矩脉动明显，其转矩脉动率达到31.03%，正弦补偿型TSF的转矩脉动率为7.58%，在该区间转矩脉动率降低了75.57%。因此，本文所提出的正弦补偿型TSF在SRM的转矩脉动和铜损耗抑制方面具备较好综合性能。