高维缺失数据的统计推断理论和方法研究

云南大学数学与统计学院

1 创新点

为突破大数据分析瓶颈，项目围绕大数据中的高维缺失数据分析的关键科学问题，开展统计推断理论和方法研究，提出筛选特征和插补缺失数据的新方法，取得一系列突破性研究成果，其主要创新点如下：

一是针对大数据的超高维问题，提出筛选特征的新方法。对大数据中的超高维异质属性数据，通过定义与属性水平相关的哑变量，提出不依赖于模型假设筛选特征的分类自适应法，可直接用于属性响应变量有偏抽样数据的特征筛选，克服现有特征筛选法没有考虑数据异质性和数据有偏抽样的缺陷；对超高维连续型数据，通过引入切片技术和数据融合思想，提出不依赖于模型假设筛选特征的切片融合均值方差滤波法，解决现有超高维特征筛选法仅适用于某一特定数据类型的缺陷；建立特征筛选方法的Sure Screening 性质和秩相合性等渐近理论。

二是针对过度识别的矩模型，提出解决模型参数推断中的不适定性问题的新方法。对不完全正确的发散维过度识别矩模型,提出同时估计模型参数和挑选变量的惩罚指数倾斜似然法，建立参数估计量和检验统计量的渐近理论，解决矩模型不完全正确时参数推断中的不适定性问题，弥补现有矩模型参数估计理论仅限于矩模型正确之不足；针对复杂抽样调查数据，通过融合抽样设计效应，构建过度识别的光滑/非可微矩模型，基于独立样本先验和相依压缩先验发展了估计模型参数和选模型的贝叶斯经验似然法，建立贝叶斯参数估计的相合性和贝叶斯置信区间的基于设计的频率性质等渐近理论，克服现有方法没有融合设计效应和相依压缩先验信息的缺陷，为复杂抽样调查数据的统计建模提供新理论、新方法。

三是针对数据缺失问题，提出插补缺失数据的新方法，建立缺失数据模型参数估计的渐近理论。对不可忽略缺失数据，基于指数倾斜模型提出不依赖于倾向得分模型的估计方程整体插补方法，克服基于倾向得分模型的传统插补法依赖于Logistic 回归模型的缺陷，开启不可忽略缺失数据模型参数估计研究的新方向；对可忽略缺失数据，提出基于缺失数据的条件分位数的插补新方法；基于提出的插补方法，对缺失数据线性模型、分位数回归模型、非光滑估计方程和非线性动态因子分析模型等发展模型参数的稳健估计和评价缺失数据机制模型合理性的贝叶斯局部影响分析，克服现有参数估计方法对异常点或重尾误差不稳健的问题，解决缺失数据机制模型“不可检验”问题；对不可忽略缺失数据估计方程，通过调整技术构建新的估计方程，建立著名的Wilks 定理，揭示了含讨厌参数的估计方程Wilks 定理不成立的原因。

图1 手写数据图

2 成果应用

一是对前瞻性样本属性（或分类）变量数据，代表作[2]对属性响应变量每一水平定义一个与之相关的哑变量，根据哑变量与特征之间的相关系数定义边际筛选统计量，在属性响应变量与特征独立的情况下证明得到：所定义的边际筛选统计量为零，这是建立分类自适应特征筛选法的一个非常重要的结论；基于边际筛选统计量的样本估计值，提出了筛选重要特征的分类自适应法；在一定的正则条件下证明了所提出的特征筛选方法不仅具有统计学上的Sure Screening 性质和秩相合性，而且能有效地克服现有超高维数据特征筛选法“不考虑数据异质性”所引起的不可靠、不稳定等不适定性问题，突破了现有超高维数据特征筛选大都仅适用于变量之间具有线性相关关系的特征筛选这一限制，解决了超高维异质性的特征筛选问题，是一种不依赖于模型假设的自适应方法。该方法应用到手写数据，其结果（见图1-2）表明，说明本项目提出的方法是切实可行的。

二是针对复杂抽样调查数据，代表作[1]通过融合抽样设计效应构造过度识别的非可微矩模型，基于独立样本先验和相依压缩先验提出了估计模型有限总体参数向量和计算参数向量置信区间的半参数贝叶斯经验似然法和挑选变量的半参数贝叶斯经验似然准则，发展了计算高效且快捷的马尔科夫链蒙特卡罗算法，证明了基于设计的贝叶斯经验似然后验分布满足“Bernstein-von Mises定理”、基于一般抽样设计的贝叶斯经验似然估计量具有相合性、基于半参数贝叶斯似然的模型选择准则在候选模型包含正确模型下具有模型选择的相合性（即依概率1选择正确模型）、基于不等概率抽样设计的贝叶斯置信区间能达到预先指定的覆盖概率，基于设计的贝叶斯经验似然方法克服了在模型框架下非抽样调查数据分析需要数据独立同分布假设、没有考虑融合设计效应和相依压缩先验信息的缺陷，基于设计的马尔科夫链蒙特卡罗近似算法解决了计算边际似然函数涉及多重积分的问题，基于样本经验似然函数的贝叶斯方法克服了经典方法对复杂抽样设计问题普适性较弱的缺陷，为估计复杂抽样调查数据中的非可微参数（如总体分位数）提供了新理论和新方法。数值模拟结果（见表1）表明，本项目提出的方法是切实可行的。

三是针对不可忽略缺失数据的半参数估计方程，在没有指定倾向得分的参数模型形式的情况下，提出了不依赖于倾向得分模型的估计方程整体插补方法，克服了传统基于倾向得分模型的缺失数据插补法依赖于Logistic回归模型假设的局限性，拓展和发展了传统缺失数据插补技术，开启了不可忽略缺失数据模型参数估计研究的新方向。基于此插补技术，提出了估计PS的基于验证样本和半参数经验似然法，将辅助信息融于Calibration条件极大地提高了倾向得分估计的效率；通过构造逆概率加权估计方程、增广逆概率加权估计方程提出了估计模型参数的广义矩估计法、广义经验似然估计法。数值模拟结果和实例数据结果发现：即使错误指定倾向得分参数模型的函数形式，参数的广义矩估计量仍具有相合性，且基于倾向得分参数模型的广义矩估计法能极大地改进现有参数估计效果；将广义经验似然法和广义矩估计法结合对过度识别半参数估计方程建立了新的参数估计理论，避免了现有单一参数估计方法的有偏性或效率低等问题。

表1 模拟结果

表2 模拟结果

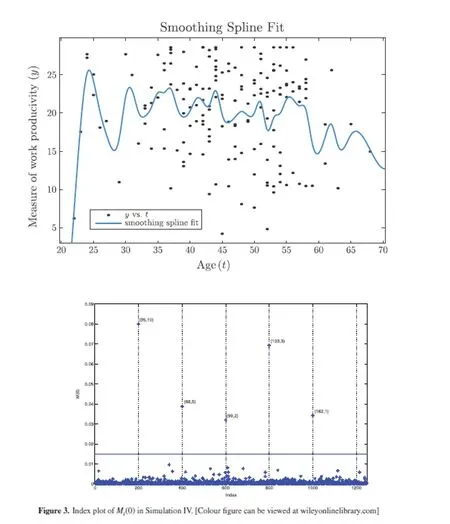
图2 模拟结果

四是针对含不可忽略缺失数据的非线性动态因子分析模型，通过用Dirichlet Process先验近似时间序列参数的分布，发展了估计模型参数和动态因子的贝叶斯方法，综合Gibbs抽样技术和Metropolis-Hastings算法提出了计算模型参数和动态因子的贝叶斯估计的混合算法；通过视扰动模型为微分几何中的流形，借助微分几何的理论给出了度量模型扰动大小的度量张量（Metric Tensor）的定义，发展了评价模型微小扰动的贝叶斯局部影响分析方法。模拟验证（见图3）：这一方法不仅能识别数据集中的强影响点，更重要的是可用来判断先验分布假设和缺失数据机制模型的合理性，解决了缺失数据机制模型“不可用数据检验”这一难题。