基于ABAQUS的轻卡动力总成悬置系统强度分析与方法研究*

赖余东，吴和兴

(江铃汽车股份有限公司 产品研发中心，江西 南昌 330052)

0 引 言

轻卡动力总成的悬置系统是车辆的关键部件之一，一般采用的是由金属零件和橡胶零件组成的橡胶悬置方案，其中金属零件起到支撑和限位作用，保证车辆安全性；橡胶零件则起到减振吸能的作用，为车辆舒适性做出贡献。悬置系统一般布置有多个悬置点，常见的有3点式或4点式布置，每个悬置点又包含连接动力总成的主动端和连接车架的被动端。在车辆实际使用过程中，恶劣的载荷工况可能导致金属零件或橡胶出现磨损或断裂失效，这就要求悬置系统具有足够的强度性能。

然而，目前对橡胶悬置系统的研究主要集中在NVH性能[1-2]以及橡胶强度耐久特性[3-4]，对金属零件的强度性能研究多以悬置支架为研究对象[5-6]，而悬置自身金属零件的强度性能研究则鲜有报道。其原因在于，目前基于CAE的悬置系统强度分析方法需要先获取悬置点弹性中心处的工况力[7]，并以弹性中心点作为加载点，将每个悬置点的主、被动端构件分别校核强度。而悬置系统工作时常常会发生限位接触、大变形等非线性力学行为，此时将主、被动端构件分别校核，则分析结果不能有效反映限位发生时悬置零件(金属、橡胶)的应力分布，从而无法准确校核其强度性能。针对这一问题，笔者提出一种包含动力总成和悬置系统的整体式悬置系统金属零件强度有限元分析方法。该方法充分考虑了悬置系统受力过程中的材料、几何、边界非线性因素，通过整体式的建模方式，实现了动力总成与悬置系统间的运动协调，分析结果更加真实可靠。

1 整体式分析方法

悬置系统的受力主要来自于动力总成工作产生的自身动载荷以及车辆行驶过程中的加减速、转弯、路面颠簸、碰撞等情况下的惯性力载荷。在工程实践中，已经归纳出能够覆盖上述载荷的基于惯性力和自身动载荷的强度校核工况体系[7]。以某轻卡4点式橡胶悬置系统的前悬置点为例，其结构如图1所示，悬置主动端4连接悬置支架2，被动端5连接悬置支座3，主动端和被动端通过硫化橡胶6连接。按一般分步式分析方法，该悬置系统强度校核需要分两步完成，如图2所示,先利用多体动力学模型提取工况力，然后建立主、被动端有限元分析模型，最终完成强度校核。事实上，现有强度校核工况在多体动力学和有限元仿真中都可以施加，因此，可以省去多体动力学提取载荷力的步骤，直接在有限元分析中建立整体式的分析模型，利用有限元法在非线性方面的优势，将各种影响分析结果的因素考虑在内，实现悬置系统自身金属零件的强度校核。

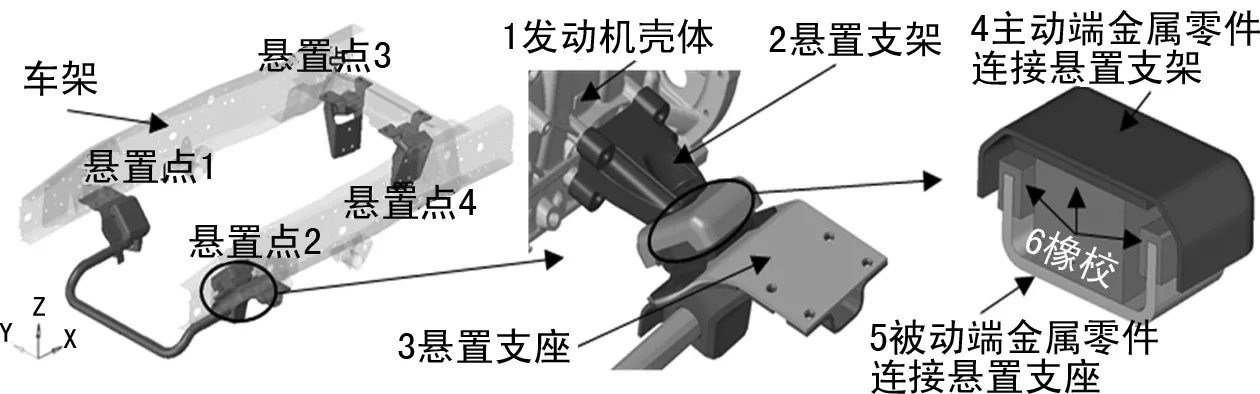
图1 某轻卡动力总成悬置系统结构示意图

图2 悬置系统分析流程示意图

1.1 分析模型的建模思路

整体式分析模型中包含动力总成及其悬置系统，其中悬置系统是主要研究对象，应该按照设计状态做详细有限元建模。而动力总成自身刚度高，质量大，因此将动力总成简化为一个质量点并赋在动力总成质心点处，并将质心与悬置系统做刚性连接，得到整体式分析模型，实现动力总成与悬置系统的运动协调。

同时，为金属骨架赋予考虑材料非线性的材料参数，为橡胶材料赋予能够反映其超弹性特性的材料本构模型及参数。为了充分考虑极限工况下悬置系统发生限位时的橡胶与橡胶、橡胶与金属骨架间的力的传递,对整个模型采用通用接触算法。因此，本模型能够更加准确地反应金属零件和橡胶的受力变形状态。

1.2 橡胶本构模型及参数确定

橡胶材料属于超弹性材料，具有非线性、各向同性、体积近似不可压缩的性质，其应力应变关系非常复杂[8],建立合适的橡胶本构模型来描述橡胶力学行为，对于仿真结果的准确性至关重要。基于唯象理论推导而来的Mooney-Rivlin本构关系模型，是工程中广泛应用的橡胶材料本构模型，大量工程实践也证明了这一模型的有效性和准确性[9-10]。其表达式为：

W=C10(I1-3)+C01(I2-3)

(1)

式中：W为应变能密度函数；I1和I2为变形张量不变量；C10和C01为橡胶材料常数。

橡胶材料常数与弹性模量E的关系为：

E=6C10(1+C01/C10)

(2)

应用该本构模型的关键在于确定橡胶材料常数C10和C01。通常情况下，需要通过多轴拉伸试验数据来计算这两个参数，这一过程周期长、费用高，而橡胶硬度的测量则相对容易和快捷。研究表明[10]，橡胶硬度与弹性模量、材料常数具有显著的相关性，并给出了拟合公式：

logE=0.0198Hr-0.5432(3)

式中:E表示橡胶材料的弹性模量；Hr表示橡胶的IRHD硬度。

由上述公式可知，橡胶材料常数的比值C10/C01确定后，即可计算出C10和C01。根据参考文献[10]的结论，C10/C01=0.05时有限元结果与试验结果吻合最好。

文中橡胶的IRHD硬度为60，假设C10/C01=0.05，计算可得C10=0.7，C01=0.035。金属骨架的材料牌号为SAPH400，其屈服强度为225 MPa，抗拉强度为550 MPa,应力应变曲线如图3所示。对悬置系统定义通用接触，金属与橡胶的摩擦系数取0.7，悬置被动端与悬置支座定义通用接触，摩擦系数取0.15。

图3 SAPH440材料的应力应变曲线

2 有限元模型建立

以某轻卡动力总成悬置系统强度分析为例，建立整体式有限元分析模型，如图4所示。金属骨架以及橡胶均采用六面体单元建模，橡胶和金属骨架单元共节点，以模拟橡胶和金属的连接关系，单元尺寸3 mm，其他零件采用壳单元建模，单元尺寸8 mm。动力总成重403 kg,简化为质量点，位于动力总成质心处。以质量点作为主节点，4个悬置点上的安装孔中心和动力总成扭矩输出点作为从节点，建立刚性单元，形成整体式分析模型。将悬置支座与车架相连的螺栓孔全约束，模拟悬置相对车架的安装状态。在参考文献[7]所列的28个工况中，按各方向恶劣程度，挑选了8个分析工况，如表1所列，其中CAES1～5为典型工况，以应力小于材料屈服强度为评价标准 ，CASE6～8为极限工况，以最大等效塑性应变(PEEQ)小于0.01为评价标准。

图4 悬置系统整体式分析模型示意图

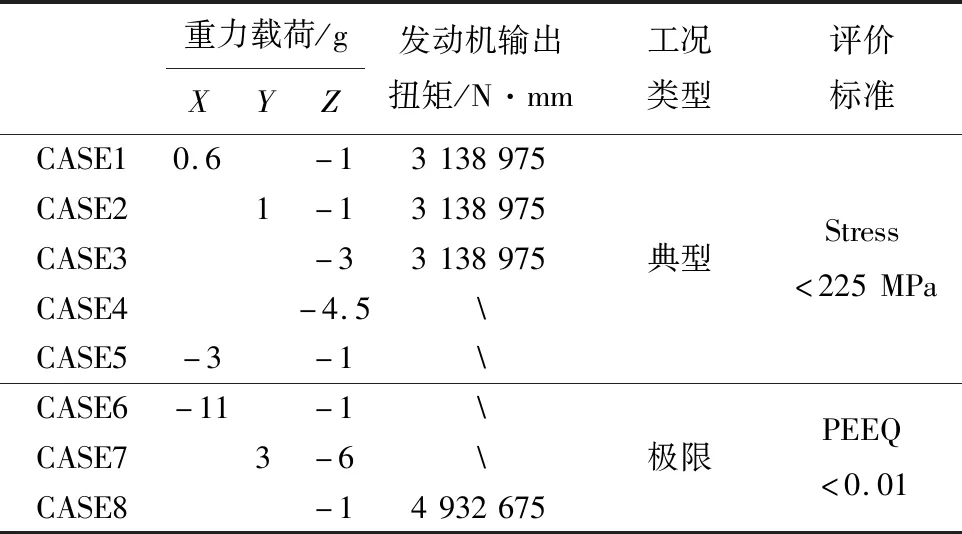
表1 悬置系统强度分析工况列表

3 有限元分析及结果

3.1 整体式模型验证

采用ABAQUS隐式求解器，以CASE6和CASE8为例，悬置主、被动端发生了严重接触行为，如图5所示。CASE6主要以-X向惯性力为主，动力总成在-X向会产生大位移运动，由于被动端固定，主动端会随着动力总成向-X方向运动，从图中可看出，被动端设计的X向限位已经起作用，接触区域橡胶被挤压变形。CASE8 主要以发动机最大输出扭矩载荷为主，动力总成会沿曲轴轴线方向做旋转运动，此时主动端会随着动力总成按图示箭头方向转动，接触区域的橡胶也已经被挤压变形。可见，整体式分析方法能够很好地描述悬置的限位作用以及橡胶在限位过程中对金属骨架的保护作用，同时也表明整体式方法得到的结果更接近实际状态。

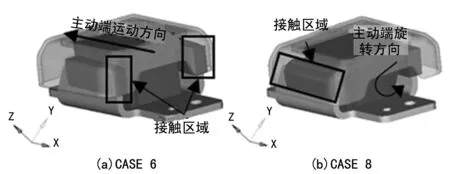
图5 限位接触区域示意图

3.2 金属零件强度分析结果

各悬置点金属零件强度分析结果如表2所列，从表2可知，在典型工况CASE1～5中，4个悬置点的金属骨架最大应力均小于材料的屈服强度。在极限工况CASE6～8中，CASE7和CASE8满足评价标准。CASE6下前悬置主动端的PEEQ达到了0.025，超过了目标值0.01，如图6(a)所示，PEEQ发生在主动端与被动端的X向接触区域，该处由于是圆角区域，属于特征变化的过渡区域，实际情况下在此处发生开裂的概率很大。针对这一风险，提出将材料牌号由SAPH400提升为SAPH440。更换材料后，该区域PEEQ下降为0.008，如图6(b)所示，满足评价标准，开裂风险消除。优化方案实施后，样车顺利通过了5万km的综合道路耐久测试。

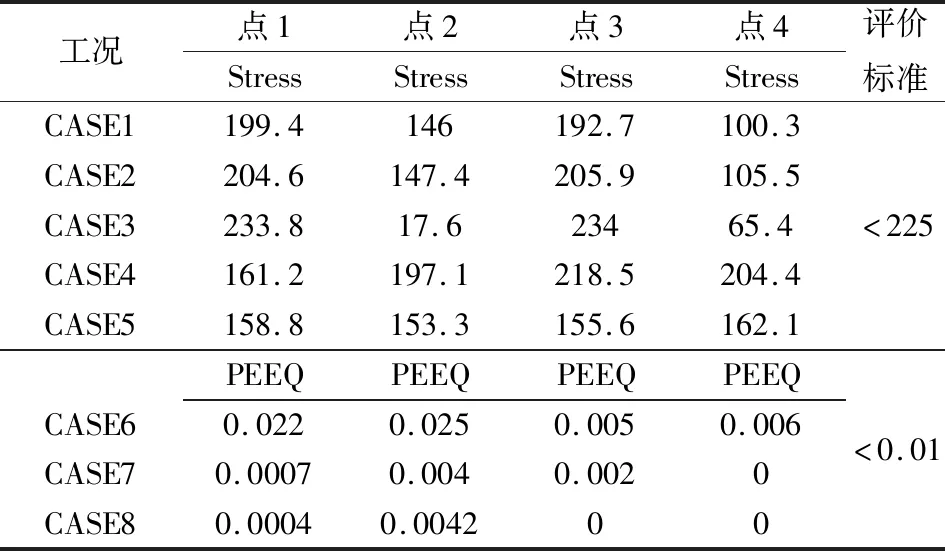
表2 各悬置点金属零件强度分析结果

图6 前悬置主动端在CASE6下PEEQ结果云图

4 结 语

整体式分析方法采用对悬置系统详细建模的思路，将主、被动端通过橡胶关联为整体有限元模型，并赋予橡胶零件合适的本构模型以及考虑分析模型中的非线性因素，分析结果表明，各零件间的相对运动关系和零件强度风险区域均与设定工况相符。因此，整体式方法相比分步式方法具有考察全面、分析精度高的优点，对悬置系统的结构强度设计具有更高的参考和指导意义。