非对称悬索桥力学特性分析

2022-09-14降星

交通世界 2022年23期

降星

（东南大学土木工程学院，江苏南京 214135）

0 引言

大跨度悬索桥作为近年来大力推广与应用的一类桥梁形式，具有外观优美、跨越能力强的优势。但是，非对称悬索桥与对称悬索桥在几何形式、力学性质上均存在一定差异。虽然目前国内外学者针对悬索桥开展了较为深入的研究，但对于非对称悬索桥的力学特性的认识仍不够全面。对于悬索桥的竖弯、扭转估算方法未将跨径不同、主塔高度不同等因素纳入考虑范畴，导致非对称悬索桥设计中的理论支持不足。

本文以非对称悬索桥的静、动力特性为研究对象，深入探究了其各项参数的敏感性，讨论了非对称及对称悬索桥在力学性能上的差异，旨在为非对称悬索桥设计提供更完善的理论支撑。

1 工程概况

以某桥梁工程为例，该桥梁主跨长1 386m，采用单跨非对称悬索设计，主缆的跨径布置为330m+1386m+205m，横向缆绳间距为27m，中跨位置主缆在成桥状态下的垂跨比为1/10，中心理论垂度为138.6m。该桥梁的设计为双向四车道，设计速度为80km/h，荷载等级为公路-Ⅰ级。

2 有限元模型建立

2.1 离散单元模型

采用Midas Civil 2019进行模型建立及有限元计算。考虑到有限元分析的精度及效率要求，将桥梁结构有限元模型共划分为1 037个节点及1 033个单元。结构缆索部分通过拉索单元进行定义，而墩柱、加劲梁及横向则通过梁单元进行定义，结构所受荷载按照结构实际状态统计。调整模型方向，使坐标轴x,y,z方向分别对应沿桥向、横桥向以及垂桥向[1]。由此得到在不考虑桩基影响下的桥梁模型，如图1所示。

图1 桥梁有限元模型

2.2 边界约束

严格按照桥梁实际建设情况确定边界条件，具体为：缆索下部与主梁交接位置为刚接；索塔底部缆索位置为固结连接；横梁与索塔之间为刚接；主梁与索塔之间为弹性连接，用以近似反映单支座的连接形式。各位置处的边界条件如表1所示。

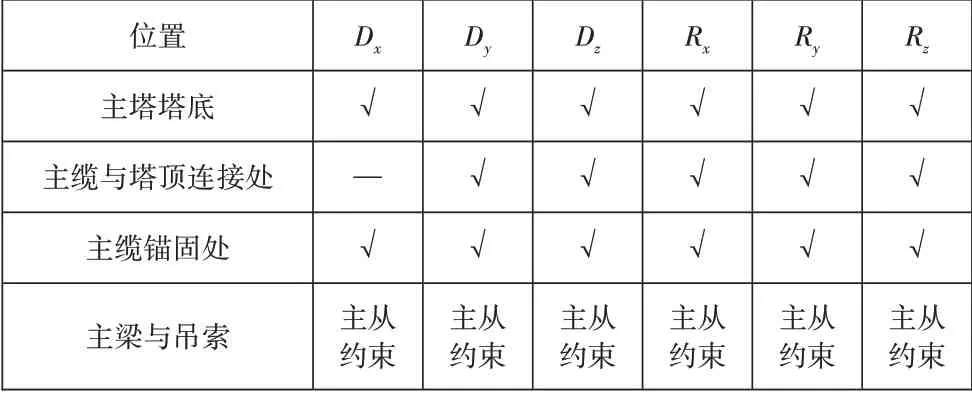
表1 各位置处的边界条件

3 成桥状态下的静力特性分析

成桥后，该桥梁结构能够在自重作用下达到平衡状态，这一状态也被称为桥梁初始平衡。记录并分析该状态下的缆索坐标、应力即可确定结构的初始状态。一般而言，桥梁在成桥状态下的静力特性，主要包括初始平衡状态分析及其他外力作用下的状态分析[2]。

3.1 恒载作用分析

桥梁结构自重及二期恒载大多需要借助吊杆传导至主缆位置，但这种传力体系会导致结构存在初始几何刚度。成桥恒载作用下吊索的轴力结果如图2所示（本结构中桥梁两侧缆索、吊杆对称分布，因此仅给出其中一侧的轴力分布情况）。

图2 成桥恒载作用下吊索的轴力

由图2可知，在接近索塔位置的1#及127#吊索表现出较高的轴力水平，其中最大轴力出现在1#吊索位置，其峰值为1 390.156kN。在上部恒载的作用下，除了吊索结构位置外，由索塔位置向跨中位置，吊索轴力逐渐趋于平稳。这间接表明了“索膜结构假定”的科学性，同时验证了恒载是顺吊杆传给主缆。

3.2 移动荷载分析

在计算成桥状态下的结构应力状态，当受到其他类型荷载作用时，即会自动识别并将“索单元”转变为相应的“析架单元”，进而将处于初始平衡下的主缆、吊杆换算为相应的几何刚度，从而完成其他静力荷载下的线性分析[3]。有限位移法在实际应用中有较好的精度，因此本文采用该方法进行分析。

进行移动荷载的满载分析时，仅考虑全桥布置情况。按照设计要求，本项目的荷载等级为公路-Ⅰ级，双向四车道标准，基于现行规范，充分考虑纵、横向的折减，按照影响线加载。

（1）主跨位移分析

在移动荷载满载分布情况下，结构最小、最大竖向位移结果显示：移动荷载满载分布下，主跨加劲梁、主缆的最大上挠度和最大下挠度分别为1.060m,1.743m，且均出现在主跨的四分点位置。有限元分析结果显示，结构挠度满足规范要求。

（2）缆索系统内力分析

在移动荷载满载分布的情况下，主缆的内力增量及内力情况表明：移动荷载满载分布下，主缆内力增量峰值出现在索鞍位置，最大值为24 236.988kN；主缆内力峰值也出现在索鞍位置，最大值为302 937.235kN。此外，边跨分布不对称导致主缆内力及其增量表现出一定的不对称性。吊索内力增量及内力情况表明：移动荷载满载分布下，吊杆构件内力增量峰值出现在跨中位置，最大值为591.609kN；吊杆构件内力峰值出现在岸侧边，最大值为1 911.521kN。在移动荷载满载分布情况下，跨中位置吊杆内力增量高于边跨，但其内力水平可视为对称分布。

4 成桥状态下的动力特性分析

非对称悬索桥与对称悬索桥的动力特性一般存在显著差异，本文主要针对主缆边跨跨径不等的情况展开分析，并将其与对称悬索桥进行对比，研究二者之间的差异性，同时也分析主塔抗弯刚度、矢跨比等参数对于桥梁动力特性的影响[4]。

以该工程项目实例为基础，借助Midas Civil 2019建立模型并计算，同时在几何非线性基础上研究结构动力特性，分析非对称敏感参数的影响。考虑到悬索桥自身具有较大的柔性，因此在确定其特征值时往往比较复杂，首先应当基于非线性分析计算得到结构的初始单元内力，从而明确恒载下的成桥状态，再开展动力特性分析。

对于非对称悬索桥而言，其动力特性应当重点关注自振频率和振型，这两个指标反映了结构自身的整体刚度及刚度分布。自振频率作为结构振动的固有指标，是开展后续动力研究的基础和关键。对悬索桥振型的研究则主要在于明确结构的振动特性，例如其固有频率及各阶振型，并将其作为结构抗震设计的基本参数。

在实际工程中，非对称悬索桥受到几何约束的限制，其所发生的振动往往并非单一的位移，而是会出现多个方向的位移耦合。本文将常见的振型归纳为4类：纵飘、竖弯、横弯及扭转。

为了探究主缆边跨不等对于结构自身频率可能产生的影响，下面以该工程为例，分别以长边跨和短边跨为等边跨建立了两座对称悬索桥模型，且以前20阶振动频率和振型特征作为研究对象。

4.1 对称悬索桥动力特性分析

（1）长边跨为对称结构的悬索桥

对于按照长边跨设计的对称悬索桥，通过有限元分析软件建立相应模型并求解其自振频率，即可得到结构前20阶振型和自振频率。分析发现：①其振型为一阶正对称横弯，频率、自振周期分别为0.057 4Hz,17.415s，表现出较长的自振周期，这也符合悬索桥柔性突出的特点；②该桥为对称悬索桥，在其前20阶中未发现显著的扭转振型，这也表明弯扭耦合作用较为微弱，结构的抗扭刚度比较大；③该桥主要振型可归纳为主梁的横弯、竖弯、纵飘和主缆的横向、竖向振动以及主塔的纵向弯曲和侧振。

（2）短边跨为对称结构的悬索桥

对于按照长边跨设计的对称悬索桥，通过有限元分析软件建立相应模型并求解其自振频率，即可得到结构前20阶振型和自振频率。通过对比可以发现，两种结构的力学状态较为类似。

4.2 非对称悬索桥动力特性分析

对该桥梁结构建立相应的有限元模型并进行动力特性分析，可得到前20阶的自振频率及振型特征，如表2所示。

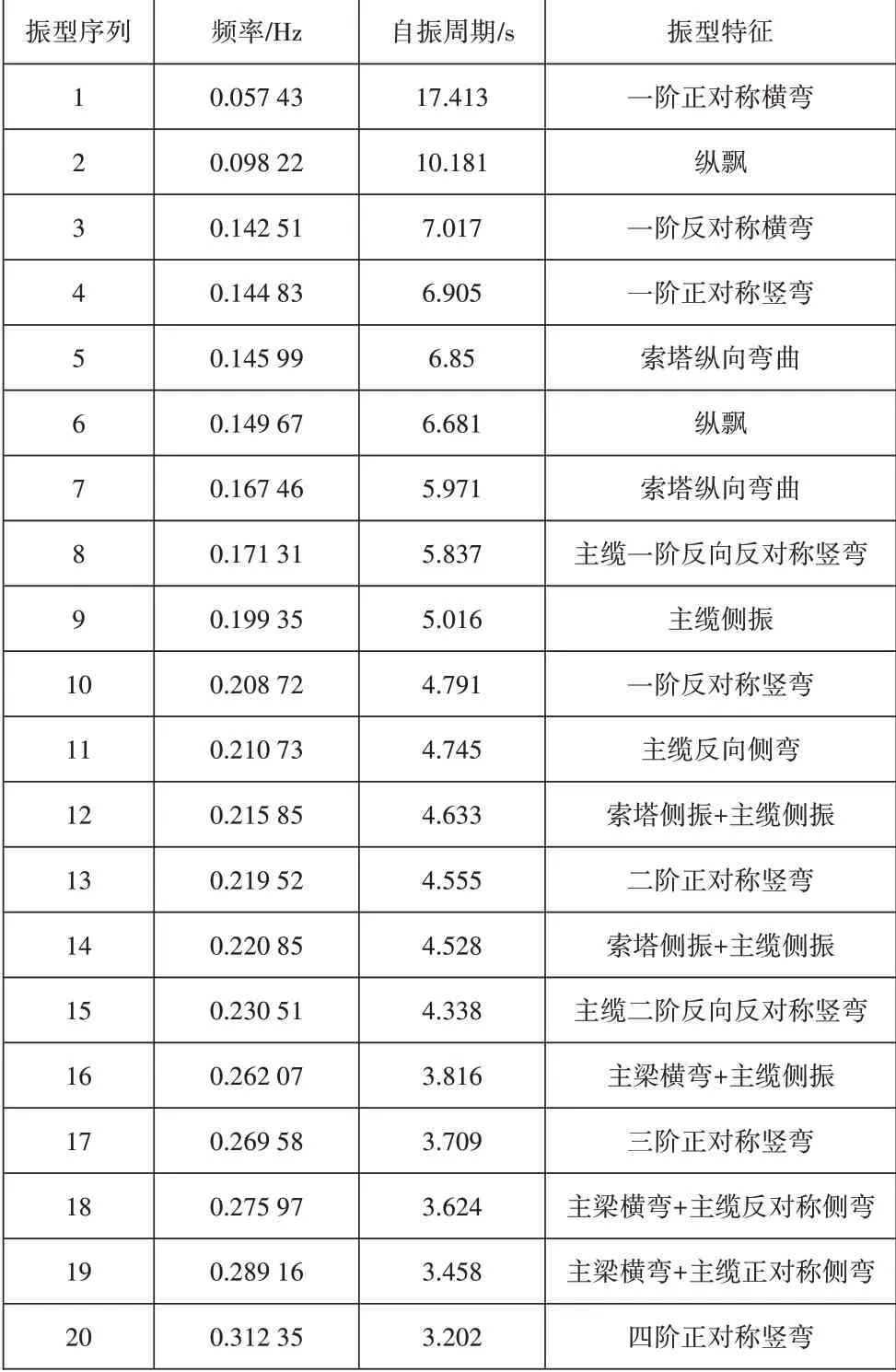
表2 非对称悬索桥自振频率及振型特征

通过有限元模型分析可知：①其振型为一阶正对称横弯，且频率、自振周期分别为0.057 43Hz,17.413s，与悬索桥柔性的特点相符，该桥为对称悬索桥，在其前20阶中未发现显著的扭转振型，这也表明弯扭耦合作用较为微弱，结构的抗扭刚度比较大；②该桥所发生的主要振型可归纳为主梁的横弯、竖弯、纵飘和主缆的横向、竖向振动以及主塔的纵向弯曲和侧振；③在早期主要为以加劲梁为主的低阶振型，在第6阶出现了索塔的纵向弯曲；④在该桥的前20阶中并未发现显著的扭转振型，且其弯扭耦合效应不显著，因此可认为结构的整体扭转刚度较大。