时空耦合畸变对超快超强激光参数测试及性能评估的影响*

龙天洋 李伟 许浩天 王逍

1) (四川大学物理学院,成都 610044)

2) (中国工程物理研究院激光聚变研究中心,绵阳 621900)

3) (中国科学技术大学光学与光学工程系,合肥 230026)

4) (山东大学(威海)空间科学与物理学院,威海 264000)

5) (中国工程物理研究院研究生院,北京 100088)

在大型超快超强激光系统中,随着光谱带宽及光束口径的增加,时空耦合畸变会变得越来越显著,该效应不仅会使光束质量恶化、影响激光的聚焦功率密度,而且会使常规的激光远场性能的评估手段失效.本文以激光器中常用的扩束透镜组为例分析了时空耦合畸变给激光参数测量及激光性能评估带来的影响.结果表明,在一个超短脉冲激光系统中,一对普通的扩束透镜组引入的时空耦合畸变不仅会使远场峰值功率密度急剧下降,还会导致单次自相关仪在近场处测得的脉宽与远场处的实际脉宽相差超过10 倍,而这种情况下利用近场脉宽测试值估算远场处的聚焦功率密度会比真实值高出一个量级.研究结果可以为激光器的优化设计、激光脉冲参数的精确表征以及相关的物理实验提供参考.

1 引言

超快、超强激光为人们提供了前所未有的极端物态条件与全新的实验手段,在许多领域已成为重要的、甚至是不可替代的工具[1-4].随着激光强度不断提高[5],人们对光束质量及激光参数精确表征的要求越来越高,国内外数拍瓦激光纷纷涌现,更高强度的激光设施也已在筹建或规划中,而时空耦合畸变已成为越来越不可忽视的因素[6,7].时空耦合畸变是指在光束横截面内看,不同空间点处的激光脉冲的时域特性(脉冲宽度、时间波形、点点之间脉冲的相对延时等)不一样,与理想状况相比产生了畸变(此时光场不再能表示成时间项和空间项分离的形式,即E(x,y,t)f(t)·g(x,y) .该效应不仅会使激光的聚焦功率密度下降,还可能影响人们对激光参数的测试与评估.例如,目前针对高能量、低重频的大型超快超强激光系统,评估其聚焦功率密度常规的做法是: 利用单次自相关仪在近场测得的脉宽代表激光脉冲远场处的脉宽,依此(结合能量和焦斑大小)计算得到远场处的功率密度.但是,这样的测试评估方法在激光脉冲具有时空耦合畸变时是否还有效? 测试值和实际值会有多大的偏差? 这些问题目前并没有人做出回答.

本文拟从激光器中常用的一种组件—扩束透镜组入手,详细考察其引入的时空耦合畸变对激光脉冲近、远场空-时特性(不同空间点的时间特性)的影响,在此基础上定量分析当“时空耦合畸变”存在时采用目前常用的激光远场性能测试/评估方法得到的参数与实际值会有多大偏差.

已有的一些对透镜色差的分析,大多是基于光线追迹的方法、利用ZEMAX 软件分析其对远场聚焦性能的影响[7],另有一些学者则利用解析的方法对透镜等元件引入的脉冲前沿进行过分析[8],但是这些处理方法都无法将具有“时空耦合畸变”的光场分布与激光参数测试过程耦合起来.本文拟采用数值模拟的方法,以一种较为全面、形象的方式展示透镜组引入的时空耦合畸变对激光近、远场三维空-时分布的影响,在此基础上结合目前常用的单次自相关脉宽测试方法,模拟分析将其用于测试此类具有时空耦合畸变的激光脉宽时测试结果的有效性,进而分析该方法用于进行远场功率密度评估时与实际值之间的偏差,以期为激光器的优化设计以及激光参数的精确表征提供依据.

2 理论分析基础

2.1 扩束透镜组

扩束透镜组是激光器中常用的一种元件,通常由两块正透镜纵向排列而成,透镜间距为两透镜焦距之和(注: 宽带光情况下此值针对中心波长).透镜的焦距与透镜材料折射率和前后表面曲率半径有如下关系:

其中n为材料折射率;f为透镜焦距;k为入射光波数;x,y为所研究平面内某点的坐标;P(x,y) 为透镜的孔径函数,定义为

其中r0为透镜圆形孔径的半径.

对于实验室中常用透镜材料的色散,可以由柯西色散公式表示:

其中λ为波长,单位 n m ;针对K9 玻璃材料(后面我们将基于此进行模拟分析),对应的柯西色散系数A=1.50805±0.00107,B=2588.92498±535.19256,C=1.92102×108±6.24×106[9-11].

2.2 激光脉冲传输分析计算模型

传输过程如图1(a)所示,一束具有一定口径的宽带超短脉冲激光经过一个扩束透镜组后再由一个理想的元件(如理想的离轴抛物聚焦镜)聚焦,考察近、远场光束的空-时特性.

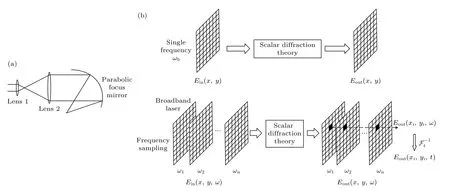
图1 (a) 光路示意图;(b) 计算示意图Fig.1.(a) Schematic of the optical path;(b) schematic of calculation.

分析处理方法(如图1(b)所示).将输入的宽带激光脉冲看作一系列单色波的叠加,再针对频率进行采样.对每一个频率的单色光分别采取下述计算过程: 光场与透镜1 的传递函数相乘用于模拟激光穿过透镜1 的效果;利用菲涅耳衍射计算激光从透镜1 后表面传播到透镜2 前表面的过程;光场与透镜2 的传递函数相乘用于模拟激光穿过透镜2 的效果;利用夫琅禾费衍射模拟激光传播至远场的过程.在完成上述过程后,就得到了远场(焦平面)每一点的各频率激光的电场,之后对每一点进行傅里叶逆变换即可由频域转换到时域,得到焦平面上不同位置的光场的空-时分布.

这其中会用到菲涅耳衍射公式[12]:

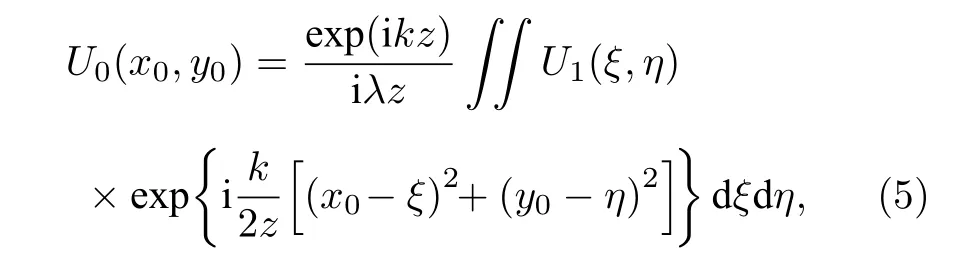
其中U1(ξ,η) 为源场光场;U0(x0,y0) 为观察面光场;λ为光束波长;z为源场到观察面光场的距离;k为光束的波数.由于其形式复杂,计算繁琐,在实际模拟计算中常利用源场光场的傅里叶变换与传递函数傅里叶变换相乘之后做逆傅里叶变换来计算观察面光场:

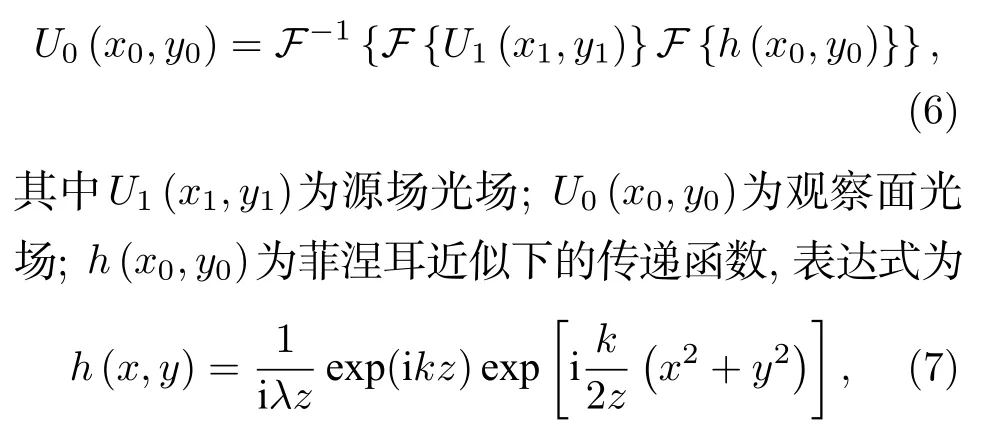
其中λ为光束波长;z为源场到观察面光场的距离;k为光束的波数.

在计算远场时使用夫琅禾费衍射公式,其傅里叶变换形式如下:

2.3 单次自相关仪脉宽测量模拟分析模型

单次自相关仪由于调试简单、使用方便,目前是(高能量、低重频)大型超短脉冲激光器上常用的测试脉宽的仪器.其基本原理如图2 所示[13]: 待测激光一分为二成为两束激光(两束光的空-时特征认为是一致的)、以一定的夹角入射到非线性晶体、在晶体中通过非共线和频效应产生二次谐波(此信号仅在两束光空间和时间上均交叠的区域内产生,并由两束光夹角平分线方向出射),在重叠区域的每一点,产生的二次谐波信号的强度S正比于每一路径上局部光强I(t) 的乘积,即有

图2 单次自相关测试原理及分析模型示意图Fig.2.Schematic diagram of the single-shot autocorrelation principle and analytical model.

其中τ为距中心x距离处两脉冲的相对延时的一半;ϕ为两束光夹角的一半;c为光速.该二次谐波的空间分布(沿X方向)即对应于待测激光脉冲时间波形的自相关函数,在激光脉冲时间波形已知的情况下可以得到待测激光的脉宽.空间强度分布的自相关半高宽WFHM(Δx) 和激光脉宽tp的关系如下:

其中k0为脉冲线型修正系数[14](即针对不同线型的脉冲时间波形,其自相关函数半高宽和自身半高宽的比值).

数值模拟时将两束基频光的光场分布用两个矩阵表示: 矩阵的两维分别代表空间维和时间维,矩阵值则代表某一空间点某一时刻的光强;两个矩阵旋转一定角度(将矩阵与二维旋转矩阵相乘)后交叠(代表两束光以一定夹角射入晶体、在晶体中交叠),两个矩阵交叠区对应数值的乘积可表征该时刻产生的二次谐波信号强度,对时间维度积分(对应图2 中沿Z向积分)则可得到随x变化的自相关信号(与通常实验中用CCD 采集的信号相对应).

在两轴单位相同时,对空间进行旋转操作可以将二维旋转矩阵左乘原坐标列矩阵来得到在旋转过后的坐标系下同一位置对应的新坐标列矩阵,即

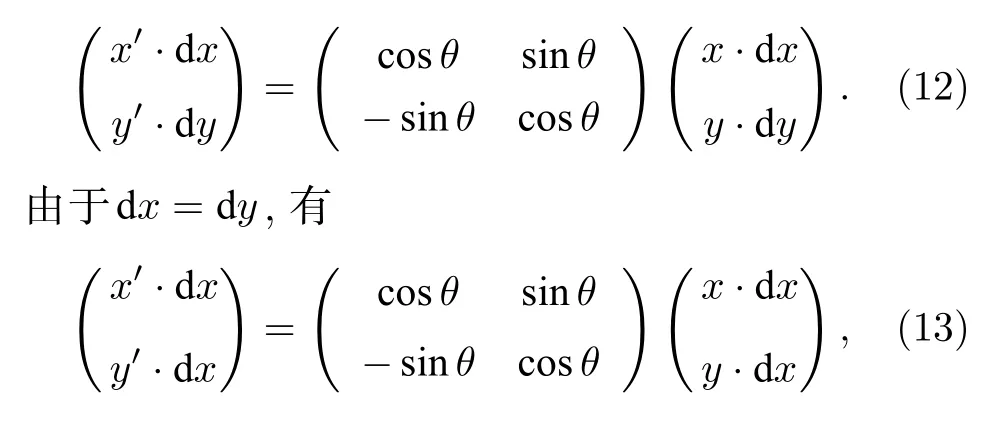
其中θ为顺时针旋转角度;x,y为旋转前坐标值(无量纲,并非实际长度);x′,y′为旋转后的坐标值.在我们的模拟分析模型中光场矩阵两轴单位不同.当两轴单位不相同时,两轴单位间有一定比例关系,当两轴单位有kdy=dx时,旋转矩阵变为

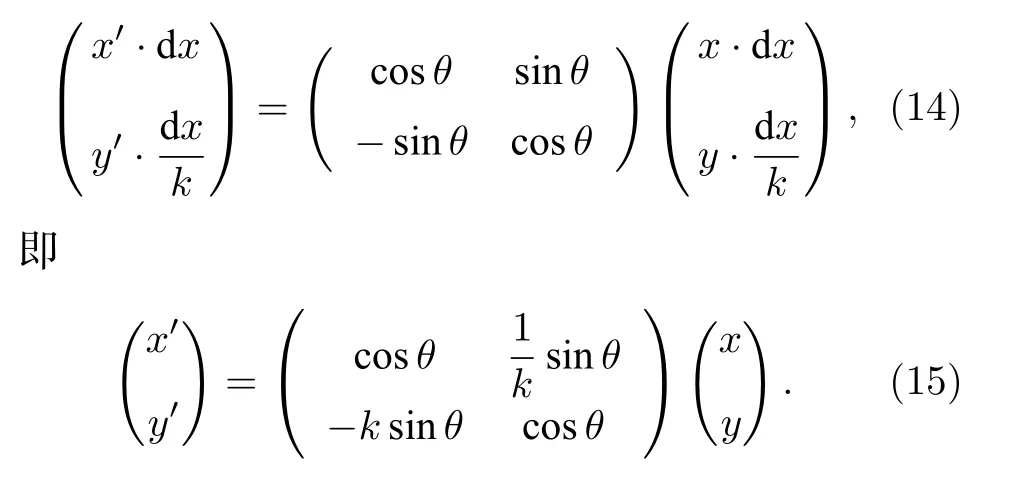
因此,当两轴单位不同时,使用(15)式即可完成旋转操作.

结合前面的时空耦合畸变分析模型和单次自相关脉宽测试分析模型可以分析近场测试脉宽和远场真实脉宽的差异,进而可以分析对比采用目前常规的评估/测算方法得到的聚焦峰值功率密度值与实际值之间的差异.

2.4 计算参数

本文中模拟分析使用的参数如表1 所列.

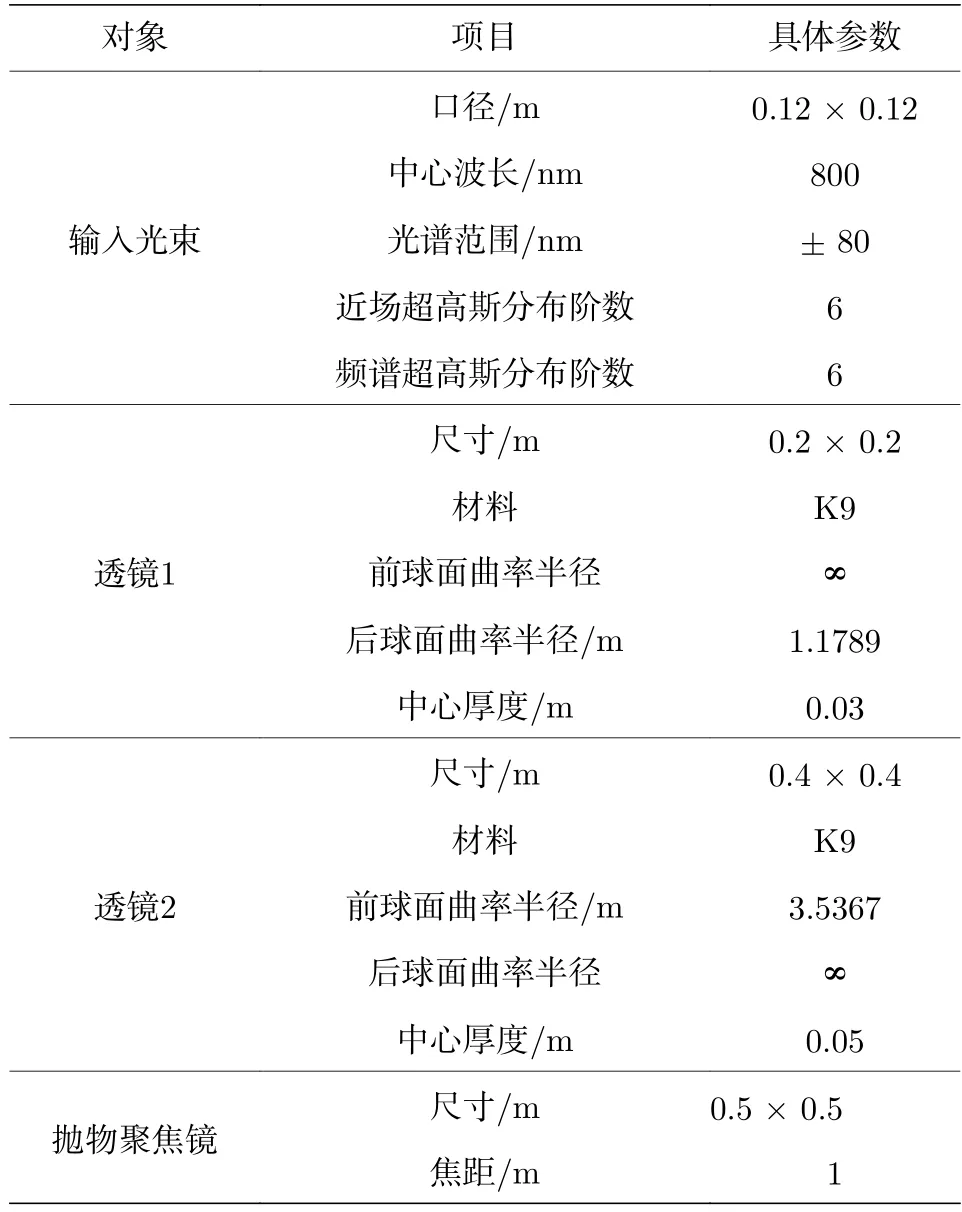
表1 计算参数Table 1. Parameters for calculation.

3 时空耦合畸变对单次自相关测试及聚焦功率密度评估的影响

3.1 扩束透镜组引入的时空耦合畸变

根据前面所述的分析计算模型及相关参数,可以得到一束理想的宽带短脉冲激光通过一个普通的扩束透镜组后产生的时空耦合畸变(见图3,三维图中纵坐标以及颜色代表该处光强大小).图3(d1)和图3(d2)是激光经过实际扩束透镜组(考虑透镜组色差)并依据光束近场的中心点进行了色散补偿[15](在实践中这是很常见的操作方法,通常是利用平行光栅对进行色散补偿)后的近、远场空-时分布,此时相当于在整个光束口径内均依据中心点处的色散进行谱相位调整(最终只能使中心点处的色散补偿至较好状态).

图3 扩束透镜组引入的时空耦合畸变 (a1) 考虑透镜组色差时远场光斑;(a2) 理想情况下的远场光斑;(b1) 考虑透镜组色差时远场环围能量曲线;(b2) 理想情况下远场环围能量曲线;理想情况下近场(c1)及远场(c2)的光场时空分布;激光脉冲经过透镜组并依据近场中心点进行色散补偿后的近场(d1)及远场(d2)时空耦合畸变Fig.3.Spatiotemporal coupling distortion introduced by lens-pair: The far-field distribution with chromatic aberration of the lenspair (a1) &without chromatic aberration (a2);circled energy graph of the far-field with chromatic aberration of the lens-pair (b1) &without chromatic aberration (b2);the spatio-temporal distribution of the laser pulse in the near-field (c1) and far-field (c2) without chromatic aberration;The spatio-temporal coupling distortion in the near-field (d1) and far-field (d2) in case of the laser pulse passing through the lens-pair with dispersion compensation according to the near-field centroid.

从图3(a)中可以看到,在宽带条件下,透镜组的色差会导致远场焦斑明显增大,焦斑面积(光强大于最大值的部分)在理想情况下仅为 6.1 μm2,在透镜组色差的影响下会扩大至 1 86.3 μm2(扩大了约30 倍);对应的焦斑半径分别为1.4 和 7.7 μm,如图3(b)中红色星标所示;另外,激光脉冲经过一个普通的扩束透镜组后产生了显著的时空耦合畸变,如图3(d)所示,初始仅十几飞秒的激光脉冲,经过透镜组后在光束截面内看,近场与中心点距离不同的位置产生了不同的延时,边缘和中心的相对延时达到了数百飞秒,各处的脉宽也明显不一致,即便依据光束中心的色散量进行了补偿,和理想情况(图3(c))相比,无论是近场还是远场依然存在较大的时空耦合畸变,远场脉宽也明显增加,半高宽达到理想情况的10 倍以上.在透镜组色差的影响下,输出激光的聚焦功率密度下降至理想情况的1/300以下(焦斑面积扩大了30 倍,脉宽变大了10 倍).

同时,扩束透镜组色差导致的时空耦合畸变与光束口径和光谱带宽之间存在显著的相关性.图4(a)显示了远场脉宽、焦斑面积和远场功率密度随光束口径的变化.图4(a1)表明,随着光束口径增加,透镜组色差会导致远场脉冲宽度明显增加,而无色差的理想情况下远场脉宽不随光束口径改变;图4(a2)表明考虑色差时,远场焦斑面积几乎不随光束口径改变,而无色差的理想情况下远场焦斑面积随近场光束口径的增大而减小,这是因为衍射极限决定的艾里斑尺寸与近场光束口径成反比;远场脉宽和焦斑面积随光束口径的改变导致了远场功率密度随光束口径发生变化,在考虑色差的影响时,远场功率密度随光束口径增大而减小,而在理想情况(不考虑色差的影响)下,远场功率密度随光束口径的增加而增加,如图4(a3)所示.图4(b)显示了远场脉宽、焦斑面积和远场功率密度随光谱带宽的变化,图4(b1)表明,随着带宽增加,透镜组色差会导致远场脉冲宽度略微增加,而无色差的理想情况下远场脉宽随带宽的增加而减小;图4(b2)表明考虑色差时,远场焦斑面积随带宽增加而明显增加,而无色差的理想情况下远场焦斑面积几乎不受激光带宽影响;图4(b3)表明理想情况下远场功率密度会随带宽的增加而增加,但是考虑色差的影响时,远场功率密度却随带宽的增加而减小.综上,时空耦合畸变程度会随着光束口径和光谱带宽的增加而增加,并进一步导致远场能量的时间、空间集中度下降,使远场功率密度显著降低.

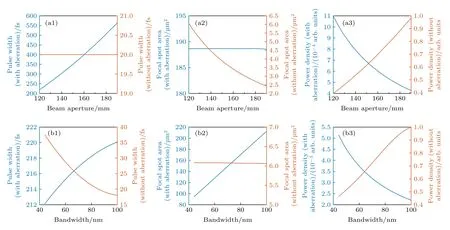
图4 考虑色差(蓝色线)和不考虑色差(红色线)时远场脉宽、焦斑面积和远场功率密度随光束口径和带宽的变化 (a1) 远场脉宽随光束口径变化情况;(a2) 焦斑面积随光束口径变化情况;(a3) 远场功率密度随光束口径变化情况;(b1) 远场脉宽随带宽变化情况;(b2) 焦斑面积随带宽变化情况;(b3) 远场功率密度随带宽变化情况Fig.4.Variation of far-field pulse width,focal spot area and far-field power density with beam aperture and bandwidth (blue line:with chromatic aberration;red line: without chromatic aberration): (a1) The variation of far-field pulse with beam aperture;(a2) the variation of focal spot area with beam aperture;(a3) the variation of far-field power density with beam aperture;(b1) the variation of far-field pulse width with bandwidth;(b2) the variation of focal spot area with bandwidth;(b3) the variation of far-field power density with bandwidth.

3.2 时空耦合畸变对单次自相关法脉宽测试的影响

实际上,时空耦合畸变不仅会使激光的聚焦功率密度急剧下降,还会影响常规参数测试结果(以及据此对激光输出性能进行评估)的有效性,图4是依据前述的单次自相关测试模型计算得到的脉宽测试结果与实际远、近场时间波形的对比(单次自相关测试中两束光的夹角为设为5°).

通过模拟分析可以看到,扩束透镜组色差导致的时空耦合畸变使激光远场脉宽增加到了理想情况的10 倍以上(图5(c1)和图5(c2));同时时空耦合畸变的存在也使得激光脉冲时间特性的表征变得很复杂,通常人们所用的简单的“脉宽”概念已经远远不能表征其复杂的空-时分布,这种情况下利用单次自相关法在近场进行脉宽测试无法反映真实的输出激光“脉宽”(远场处激光脉冲的持续时间),通常情况下自相关仪测试值偏小,文中条件下,对比图5(a3)和图5(c1),可以看到测试值与真实值相比小了1 个量级,这一结果在一定程度上说明,当时空耦合畸变较大时,常规的依据单次自相关法测试近场脉宽用以评估远场聚焦功率密度的做法与实际值会有较大偏差,通常情况下,该方法会使聚焦功率密度评估值显著偏高(文中的条件下超过1 个量级).另外,对比图5(a)及图5(b)可以看到,在有时空耦合畸变的条件下,采用单次自相关法在近场处测得的脉宽值甚至比理想情况下的还要略短,这是由于时空耦合畸变使两束光在“倍频晶体”中时间与空间均重叠的区域变小,产生的和频信号也变窄,所以基于单次自相关仪的脉宽测试方法在激光脉冲具有时空耦合畸变的条件下可靠性会急剧下降.

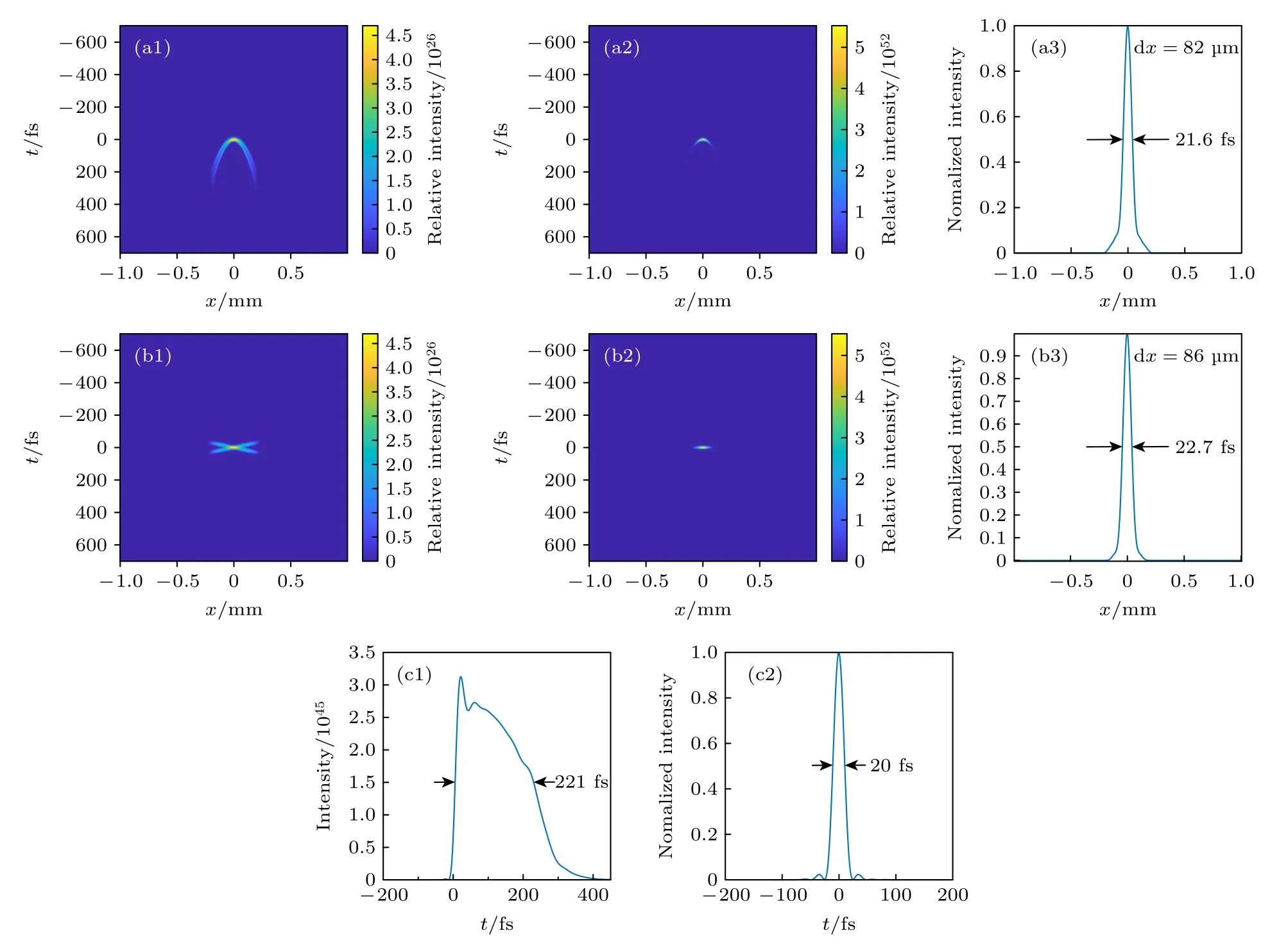
图5 单次自相关脉宽测试分析对比 (a1) 有色差时基频光信号;(a2) 有色差时单次自相关倍频信号(空-时分布);(a3) 有色差时单次自相关仪信号;(b1) 理想条件下的基频信号;(b2) 理想条件下自相关倍频信号空-时分布;(b3) 理想条件下单次自相关仪信号;(c1) 通过透镜组后远场处(焦平面内)的积分通量时间波形;(c2) 通过理想无像差透镜组时远场处的积分通量时间波形Fig.5.Analysis and comparison between the results from single-autocorrelation method and the actual far-field pulse shape: Fundamental frequency signal (a1),second harmonic signal (a2) and signal of an auto-correlator (a3) in case of the pulse passing through the lens-pair with chromatic aberration;fundamental frequency signal (b1),second harmonic signal (b2) and signal of an auto-correlator (b-3) in case of ideal condition without chromatic aberration;(c1) actual temporal shape of the pulse at the far field with chromatic aberration of lens-pair;(c2) actual temporal shape of the pulse at the far field without chromatic aberration of lens-pair.

4 结论

通过模拟分析可以看到,时空耦合畸变不仅会使激光脉冲的聚焦功率密度大幅降低(与理想情况相比一个普通的扩束透镜组会使远场峰值功率密度下降2 个量级),更重要的是它还会使目前一些常规的激光参数测量/评估手段失效(文中条件下实际远场处的脉宽与近场处用单次自相关仪测得的脉宽值差异超过了一个量级),给激光与物质相互作用的规律性研究带来困难,影响超快超强激光的应用效果.

实际上,在一个大型超快超强激光系统中,除了扩束透镜组以外,展宽器、压缩器、AOPDF(声光光谱色散滤波器)、带楔角的窗口玻璃或取样元件等都可能引入时空耦合畸变[16],因此实际系统中的综合畸变往往会比文中所述的仅由透镜组引起的畸变复杂得多,所以,发展有效的时空耦合畸变测试及控制/补偿技术是超快超强激光进一步发展的关键.