Ge-S/F 共掺杂对Li2MSiO4(M=Mn,Fe)晶体结构和性能影响的理论研究*

郭厦蕾 侯育花† 郑寿红 黄有林 陶小马

1) (南昌航空大学材料科学与工程学院,南昌 330063)

2) (广西大学物理科学与技术学院,南宁 530004)

基于密度泛函理论的第一性原理平面波赝势法,结合广义梯度近似(GGA+U),系统研究了Ge-S/F 共掺杂对Li2MSiO4 (M=Mn,Fe)晶体结构稳定性和电化学性能的影响.计算结果表明Ge-S/F 共掺杂Li2MSiO4 (M=Mn,Fe) 体系在脱锂过程中均会发生Li 和M 的位置交换,与Li2MSiO4(M=Mn,Fe) 相比,掺杂体系具有更好的韧性,且锂离子在掺杂体系中更容易迁移.同时发生了位置交换的掺杂体系结构在脱锂过程中大多更为稳定,尤其是Li2Mn0.5Ge0.5SiO3.5S0.5 在整个脱锂过程中体积变化均很小,说明其具有良好的结构循环稳定性.此外,Ge-S/F 共掺杂均降低了Li2MSiO4 (M=Mn,Fe) 的理论平均脱嵌电压.结合态密度图和磁矩结果分析表明,Ge-S/F 共掺杂可以提高Li2MnSiO4 的导电性和延缓Li2MnSiO4 体系中Jahn-Teller效应的出现,有利于提高Li2MnSiO4 的结构循环稳定性.同时,共掺杂不仅提高了Li2FeSiO4 的导电性,也有利于Li2FeSiO4 体系脱出更多的Li+,特别是Ge-F 共掺杂体系有望实现完全脱锂.

1 引言

Li2MSiO4(M=Mn,Fe)锂离子电池正极材料因具有结构稳定、理论比容量高、对环境友好等特点成为研究热点[1-3].但是,较低的电导率[4]和脱锂过程中产生的Mn3+3d 轨道电子的不均匀占据,会引起Jahn-Teller 畸变,导致Li2MnSiO4较差的循环稳定性[5,6],此外,Li2FeSiO4实际放电容量较低[7]和平均脱嵌电压较高[8],以上这些缺点并不利于Li2MSiO4(M=Mn,Fe)锂离子电池正极材料的推广应用.

为了提高Li2MSiO4(M=Mn,Fe)电池正极材料的性能,研究人员进行了大量的研究.Wang 等[9]结合实验和理论计算研究Li2MnSiO4/C/rGO 中双位点镁掺杂,结果表明Li1.98Mg0.02Mn0.94Mg0.06SiO4/C/rGO 材料具有258 mA·h/g 的高初始放电容量,100 次循环后容量保持率高达90.3%.Ma 等[10]使用微波辅助溶胶-凝胶法合成了 Li2Mn1—xCexSiO4@C (0 ≤x≤ 0.05) 纳米粒子,研究表明Li2Mn0.07Ce0.03SiO4@C 性能较好,其初始放电比容量达210.5 mA·h/g,同时具有优异的结构循环稳定性和倍率性能、较高的Li+扩散系数和较小的电荷转移电阻.Wang 等[11]研究发现Sn(II) 和 Sn(IV) 分别在Li2FeSiO4纳米晶体的Fe 和Si 位上进行共掺杂不仅能够提高体系的电导率,而且还增加了锂离子的扩散系数,同时还有效降低了平均脱锂电压,有利于从体系中脱出更多的锂离子.Li 等[12]系统研究了Mn 和Al 共掺杂Li2FeSiO4/C 材料的电化学性能,结果表明(Li2Fe0.75Mn0.2Al0.05SiO4) 的初始放电容量为159.3 mA·h/g,50 次循环后容量保持率达到78%,有效提高了系统的结构循环稳定性.密度泛函理论研究表明,S 掺杂可以提高Li2MnSiO4正极材料的延展性,且有利于提高Li2MnSiO4的比容量和结构循环性能[13].Singh等[14]研究发现Cl 掺杂可以增加Li2FeSiO4的电导率并降低脱嵌电压.Nytén 等[15]研究发现在脱锂过程中Li2FeSiO4电压会从3.1 V 下降到2.8 V,这是由于在脱嵌Li+过程中Li 和Fe 离子之间的位置交换 (SE) 引起的.

课题组前期研究发现,Ge,S 和F 分别掺杂Li2MSiO4(M=Mn,Fe) 可以在一定程度上提高体系的结构循环稳定性和电化学性能[16-18].为了全面考察掺杂对体系性能的影响,本文结合前期研究结果,系统地研究了Ge-S/F 共掺杂对Li2MSiO4(M=Mn,Fe)晶体结构和电化学性能的影响,重点讨论了Li 和M位置交换情况,并深入探讨了在脱锂过程中电荷的补偿细节.以期通过共掺杂获得性能更优异的Li2MSiO4(M=Mn,Fe)锂离子正极材料.

2 计算方法和晶体结构

2.1 计算方法

采用基于密度泛函理论的第一性原理计算软件VASP (viennaab initiosimulation package)[19,20]软件包进行计算.波函数用平面波基函数展开,交换关联能选取GGA 近似下的PBE (Perdew-Burke-Ernzerho) 形式[21],势函数选PAW 势[22],平面波截断能取为500 eV,布里渊区积分采用Monkhorst-Pack 方法生成K点为9 × 9 × 9 的网格[23].考虑Mn 和Fe 的局域3d 电子之间强的库仑相互作用,采用 Hubbard 参数进行校正[24],Mn 和Fe 的Ueff=U-J值分别为4.5 和4.0 eV[15,16].每一个晶体结构都进行了优化,直至每个原子的力收敛到0.01 eV/Å以下时,此外,所有计算均在自旋极化条件下进行.

2.2 晶体结构

本文主要针对空间群为Pmn21的Li2MSiO4(M=Mn,Fe)进行研究[13,25-27].通过一系列测试,确定了Ge-S/F 共掺杂的最佳位置、脱锂顺序以及脱锂过程中Li/M(Ge)离子的位置交换情况.通过计算能量结果发现,Li-M位置交换的LiMn0.5Ge0.5SiO3.5R0.5(R=S,F) 晶体结构能量比未发生位置交换的低1.430 和0.252 eV,同时LiFe0.5Ge0.5SiO3.5R0.5(R=S,F) 体系结构的能量差分别为0.010和0.405 eV,表明Li2M0.5Ge0.5SiO3.5R0.5(M=Mn,Fe;R=S,F) 体系在脱锂过程均发生了Li 和M的位置交换.发生位置交换的LiM0.5Ge0.5SiO3.5R0.5(M=Mn,Fe;R=S,F) 的晶胞结构如图1 所示.

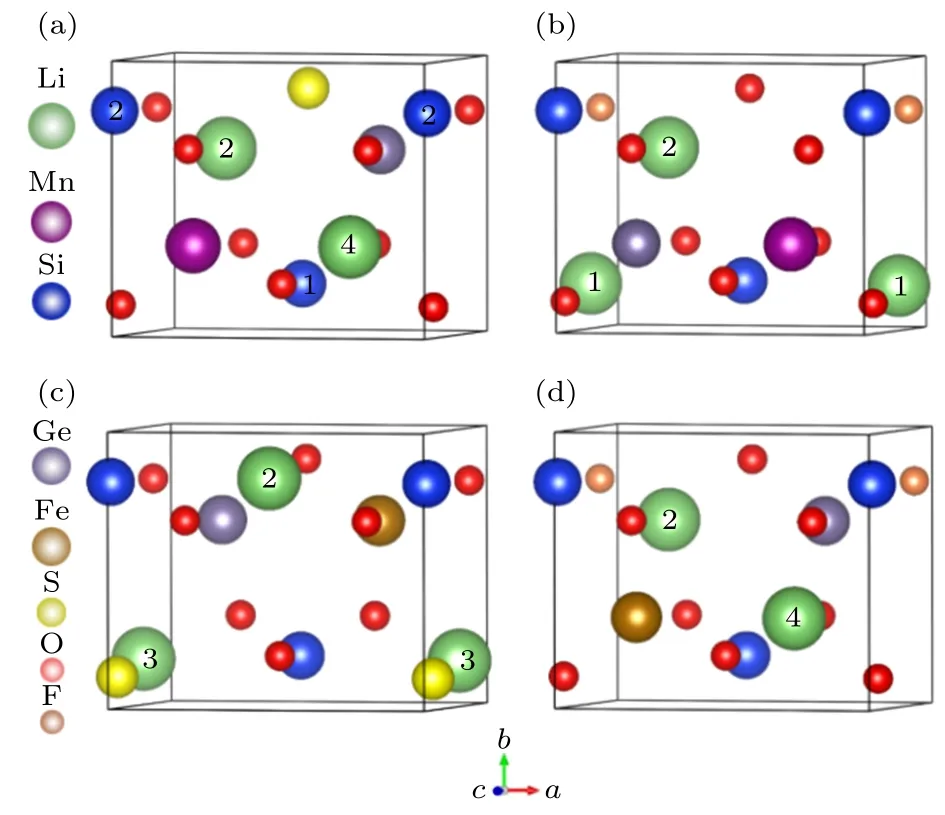
图1 (a) 位置交换的LiMn0.5Ge0.5SiO3.5S0.5 的晶胞结构;(b) 位置交换的LiMn0.5Ge0.5SiO3.5F0.5;(c) 位置交换的LiFe0.5 Ge0.5SiO3.5S0.5;(d) 位置交换的LiFe0.5Ge0.5SiO3.5F0.5Fig.1.Crystal cell structure of (a) site exchange LiMn0.5 Ge0.5SiO3.5S0.5,(b) site exchange LiMn0.5Ge0.5SiO3.5F0.5,(c) site exchange LiFe0.5Ge0.5SiO3.5S0.5,(d) site exchange LiFe0.5Ge0.5 SiO3.5F0.5.

3 结果与讨论

3.1 Li2M0.5Ge0.5SiO3.5R0.5 (M=Mn,Fe;R=S,F)结构稳定性和力学性能

弹性常数的特征值和Li2M0.5Ge0.5SiO3.5R0.5(M=Mn,Fe;R=S,F)体系的形成能可以作为判断结构稳定性的依据,本文分别计算了Ge-S/F共掺杂Li2MSiO4(M=Mn,Fe)的弹性常数和形成能,如表1 所列.一般来说,体系的弹性常数特征值为正,且形成能为负,则表明体系结构是稳定的[28,29].从表1 可以得出,Li2M0.5Ge0.5SiO3.5R0.5(M=Mn,Fe;R=S,F)体系晶体结构都是稳定存在的.

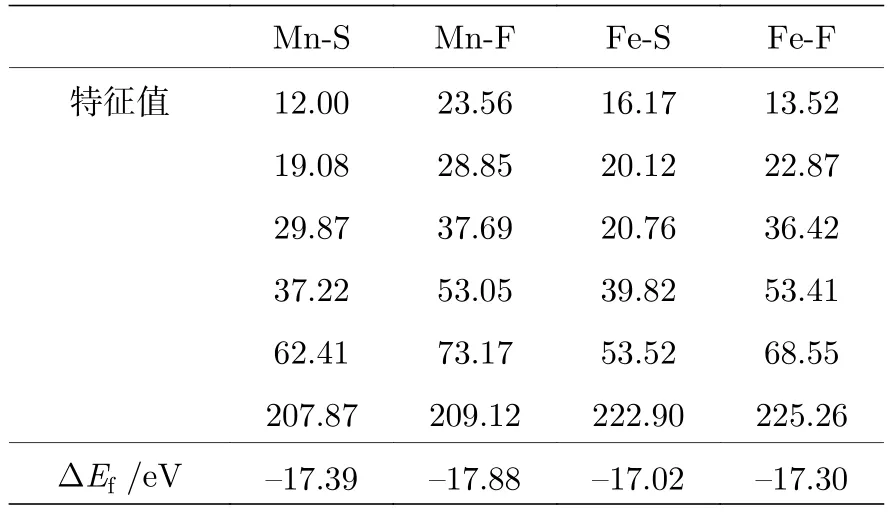
表1 Li2M0.5Ge0.5SiO3.5R0.5 (M=Mn,Fe;R=S,F)的弹性常数矩阵的特征值和形成能(ΔEf)Table 1. The eigenvalues of the elastic constant matrix and formation energy (ΔEf) of Li2M0.5Ge0.5SiO3.5R0.5 (M=Mn,Fe;R=S,F).

为了详细描述Li2M0.5Ge0.5SiO3.5R0.5(M=Mn,Fe;R=S,F)的力学性能,分别计算了体积模量B、杨氏模量E、剪切模量G、模量比B/G、德拜温度θD和泊松比ν,具体计算方法和公式参考了文献[13,30,31],计算结果如表2 所列.模量比B/G和泊松比ν可以一定程度反映材料的韧性和脆性,判断标准分别为1.75 和0.3,即当材料的模量比数值大于1.75 且泊松比接近0.3 时,说明材料具有较好的延展性[32,33].从表2 可以看出,Li2M0.5Ge0.5SiO3.5R0.5(M=Mn,Fe;R=S,F) 体系的B/G均大于1.75,且ν 接近0.3,表明Ge-S/F 共掺杂体系具有良好的韧性.此外,如果材料的杨氏模量和德拜温度较小,则说明锂离子更容易在结构中进行迁移[13].与Li2MSiO4(M=Mn,Fe)相比[34],Li2M0.5Ge0.5SiO3.5R0.5(M=Mn,Fe;R=S,F)体系具有更小的杨氏模量和德拜温度,说明Ge-S/F 共掺杂可以促进锂离子的迁移.

表2 计算的Li2M0.5Ge0.5SiO3.5R0.5 体积模量B、剪切模量G、模量比B/G、泊松比ν、杨氏模量E 和德拜温度θD (M=Mn,Fe;R=S,F)Table 2. Calculated bulk modulus B,shear modulus G,modulus ratio B/G,Poisson’s ratio ν,Young’s modulus E and Debye temperature θD of Li2M0.5Ge0.5SiO3.5R0.5 (M=Mn,Fe;R=S,F).

3.2 LixM0.5Ge0.5SiO3.5R0.5(M=Mn,Fe;R=S,F;x=0,1,2)的晶体结构参数

为了明晰掺杂体系在脱锂过程中的体积变化情况,分别计算了初始和位置交换的 LixM0.5Ge0.5SiO3.5R0.5(M=Mn,Fe;R=S,F;x=0,1,2)晶胞的体积,如图2 所示.从图2(a)可知,对于初始体系来说,LiMn0.5Ge0.5SiO3.5R0.5(R=S,F)和Mn0.5Ge0.5SiO3.5R0.5(R=S,F)的体积相比Li2Mn0.5Ge0.5SiO3.5R0.5(R=S,F)均发生了收缩,且LiMn0.5Ge0.5SiO3.5R0.5(R=S,F)体积收缩率分别为4.69%和3.99%,Mn0.5Ge0.5SiO3.5R0.5(R=S,F) 的体积收缩率分别为2.14%和1.47%.与Li2Fe0.5Ge0.5SiO3.5R0.5(R=S,F)相比,当从每单位分子式中脱去第一个锂离子时,体系的体积分别收缩了6.12%和1.13%,当锂离子完全脱出时,体积分别收缩了0.64%和4.35%.

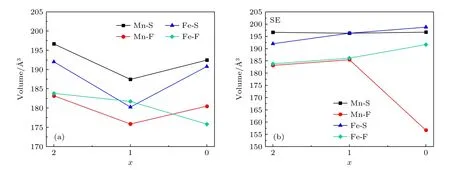
图2 (a) 初始LixM0.5Ge0.5SiO3.5R0.5 (M=Mn,Fe;R=S,F;x=0,1,2) 的晶胞体积;(b) 发生位置交换LixM0.5Ge0.5SiO3.5R0.5 (M=Mn,Fe;R=S,F;x=0,1,2) 的晶胞体积Fig.2.(a) The unit cell volume of initial LixM0.5Ge0.5SiO3.5R0.5 (M=Mn,Fe;R=S,F;x=0,1,2);(b) the unit cell volume of site exchange LixM0.5Ge0.5SiO3.5R0.5 (M=Mn,Fe;R=S,F;x=0,1,2).

从图2(b)可知,对于位置交换体系,LiMn0.5Ge0.5SiO3.5S0.5与LiMn0.5Ge0.5SiO3.5F0.5的体积 变化率分别是—0.18%和1.26%,当Li+完全脱出时,体系的体积变化率分别为0.04%和—14.45%.与Li2Fe0.5Ge0.5SiO3.5R0.5(R=S,F)相比,LiFe0.5Ge0.5SiO3.5R0.5(R=S,F)发生了体积膨胀,且变化率分别为2.22%和1.27%,同时Fe0.5Ge0.5SiO3.5R0.5(R=S,F) 的体积分别膨胀了3.53%和4.28%.综合以上分析,除Mn0.5Ge0.5SiO3.5F0.5体积收缩较大外,在脱锂过程中,位置交换体系的体积变化比初始体系更稳定,尤其是发生位置交换Li2Mn0.5Ge0.5SiO3.5S0.5,说明Ge-S/F 共掺杂有效地提高了Li2FeSiO4的结构循环稳定性.

为了详细分析掺杂体系在脱锂过程中的结构参数变化情况,图3 和表3 分别给出了初始和发生M-Li 位置交换的LixM0.5Ge0.5SiO3.5R0.5(M=Mn,Fe;R=S,F;x=0,1,2) 体系在脱锂过程中晶格常数和M(Ge,Si)—O 平均键长的变化情况.由图3 可知,初始体系的晶格常数a在脱锂过程中逐渐减小,这是由于M和Ge 离子在脱锂过程中参与了电荷补偿并氧化成更高的价态,造成M(Ge)—O 键长缩短[35].初始体系的晶格常数b随着锂离子的脱出而增加,这是因为在Li+的脱出过程中,由于沿b轴方向的原子之间键长变化和[LiO4]四面体层对其相邻的[Mn0.5Ge0.5SiO4]四面体层之间的束缚作用变化,两方面原因导致体系晶格常数b的变化.此外,由表3 可知,Fe0.5Ge0.5SiO3.5F0.5的晶格常数b减小,这是由沿b轴形成的Ge-F 键的长度缩短导致的.随着Li+的脱出,初始体系的晶格常数c发生不规则变化,主要原因是体系中键长的缩短或增加以及受沿c轴方向形成的[M0.5Ge0.5SiO3.5R0.5]四面体层褶皱变化造成的[29].随着Li 和M离子的位置交换,改变了晶体中原子本来的位置从而引起晶格中键长和相应的四面体位置变化,从而改变了体系的晶格常数变化趋势.

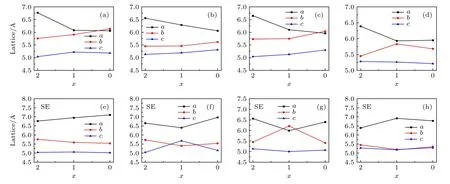
图3 初始和位置交换LixM0.5Ge0.5SiO3.5R0.5 (M=Mn,Fe;R=S,F;x=0,1,2) 的晶格常数Fig.3.Lattice parameters of initial and site exchange LixM0.5Ge0.5SiO3.5R0.5 (M=Mn,Fe;R=S,F;x=0,1,2).

表3 位置交换的LixM0.5Ge0.5SiO3.5R0.5 (M=Mn,Fe;R=S,F;x=0,1)的平均键长 (单位: Å)Table 3. The average bond length (in Å) of LixM0.5Ge0.5SiO3.5R0.5 (M=Mn,Fe;R=S,F;x=0,1) with the site exchange case.

脱锂过程中阳离子的键长、键价和 BVS 变化可用于分析阳离子参与电荷补偿情况,如当阳离子价态增加时,键长会缩短,BVS 会增加[16,36-38].为了有针对性地说明键长和键价的变化情况和关系,表4 列出了发生位置交换LixM0.5Ge0.5SiO3.5R0.5(M=Mn,Fe;R=S,F;x=0,1,2) 系统中M(Ge,Si)—O 的键价和.结合表3 和表4 的数据分析可知,由于Ge-S(F) 共掺杂原子半径不同,Li2MSiO4(M=Mn,Fe) 体系中的[MSiO4]四面体发生了一定程度的畸变,其中Si—O 的平均键长和Si 离子的BVS 变化不大,说明Si 离子在Li+脱出过程中没有提供电荷补偿.随着Li+的脱出,相应的M—O 和Ge—O 的平均键长减小,M和Ge 离子的BVS增加,如在LixMn0.5Ge0.5SiO3.5S0.5体系中,随着锂离子的脱出,Mn—O 键长从2.220 Å分别减小到2.092 和1.826 Å,其BVS 从1.42 分别增加至1.77和3.35,同时Ge—O 键从2.216 Å分别减小至1.810和1.794 Å,其BVS 从1.23 分别增加至3.60 和3.70.由数据可知,从LixMn0.5Ge0.5SiO3.5S0.5单位公式中脱去一个锂离子时,Mn—O 键长和BVS 变化不大,而Ge—O 的变化较大,说明主要由Ge 离子提供电荷补偿.当完全脱去锂离子时,Mn—O 键长和BVS 变化较大,而Ge—O 的变化不大,说明主要由Mn 离子提供电荷补偿,Mn 离子由+2 价变成+3 价.通过以上分析可知,M和Ge 离子均参与了脱锂过程中的电荷补偿,电荷补偿的详细分析将在电子结构部分给出.

表4 位置交换的LixM0.5Ge0.5SiO3.5R0.5 中(M=Mn,Fe;R=S,F; x=0,1)、Ge 和 Si 的键合价和 BVSTable 4. Bond-valence sums (BVS) of M (M=Mn,Fe),Ge and Si in LixM0.5Ge0.5SiO3.5R0.5 (M=Mn,Fe;R=S,F;x=0,1) with site exchange case.

3.3 理论平均脱嵌电压

为了阐明共掺杂对Li2MSiO4(M=Mn,Fe)体系的理论平均脱嵌电压的影响,详细计算了相关体系的理论平均脱嵌电压,计算公式在文献[15]中有详细描述,计算结果如图4 所示.从图4(a)可以看出,在Li2Mn0.5Ge0.5SiO3.5R0.5(R=S,F) 体系中,当发生一次脱锂时,初始体系的脱嵌电压分别为2.60 和2.08 V,与初始系统相比,位置交换系统的电压分别降低了0.71 和0.13 V.当完全脱锂时,初始体系的脱嵌电压分别为3.65 和3.54 V,位置交换体系的电压分别为4.15 和2.66 V.对于Li2Fe0.5Ge0.5SiO3.5R0.5(R=S,F) 体系,当第一个Li+脱出时,初始系统的脱嵌电压分别为2.54 和1.49 V,与初始系统相比,位置交换系统的电压分别降低了0.01 和0.20 V.当Li+完全脱去时,初始系统电压为3.39 和3.29 V,而位置交换系统电压分别为3.06 和 3.39 V.综合以上分析可知,一次脱锂过程中各体系的电压因Li 和M离子的位置交换而降低.此外,Li2M0.5Ge0.5SiO3.5R0.5(M=Mn,Fe;R=S,F)体系在Li+完全脱出时具有较低的脱嵌电压,表明Ge-S(F)共掺杂有助于Li2MSiO4(M=Mn,Fe) 体系中锂离子的脱出.

图4 (a) 初始和位置交换Li2Mn0.5Ge0.5SiO3.5R0.5 的平均脱嵌电压(R=S,F);(b) 初始和位置交换Li2Fe0.5Ge0.5SiO3.5R0.5 的平均脱嵌电压 (R=S,F)Fig.4.(a) Average deintercalation voltage of initial and site exchange Li2Mn0.5Ge0.5SiO3.5R0.5 (R=S,F);(b) average deintercalation voltage of initial and site exchange Li2Fe0.5Ge0.5SiO3.5R0.5 (R=S,F).

3.4 LixM0.5Ge0.5SiO3.5R0.5 (M=Mn,Fe;R=S,F;x=0,1,2) 的电子结构

通过态密度图可以分析材料的导电性,同时结合磁矩结果明晰离子参与电荷补偿的情况.本文分别计算了LixM0.5Ge0.5SiO3.5R0.5(M=Mn,Fe;R=S,F;x=0,1,2) 的总态 密度和 分波态密度(TDOS 和PDOS),同时给出了LixM0.5Ge0.5SiO3.5R0.5(M=Mn,Fe;R=S,F;x=0,1,2)体系中M(M=Mn,Fe) 离子的磁矩和相应的氧化价态,如表5 所列.

表5 初始和位点交换情况下 M (M=Mn,Fe)离子的磁矩 (µB) 和氧化态Table 5. Magnetic moment (in µB) and oxidation state of M (M=Mn,Fe) ions in the case of initial and site exchange.

图5 为 LixMn0.5Ge0.5SiO3.5S0.5(x=0,1,2)在初始和发生位置交换情况下的TDOS 和PDOS.从图5(a),(c)可以看出,Li2Mn0.5Ge0.5SiO3.5S0.5的带隙为2.74 eV,显示出半导体特性.随着锂离子的脱出,体系的带隙值在逐渐减小.当每个单位分子式中脱去一个Li+时,初始和发生位置交换体系的带隙分别为0.63 和2.66 eV,当Li+完全脱出后,初始体系呈现半金属性质,而发生位置交换的体系具有0.17 eV 的带隙宽度.

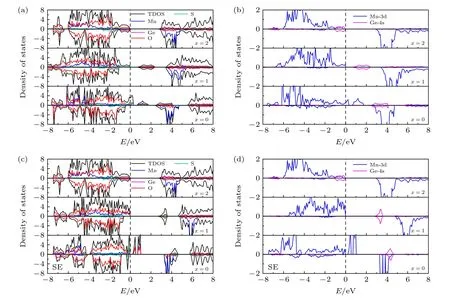
图5 (a) 初 始LixMn0.5Ge0.5SiO3.5S0.5 (x=0,1,2)的TDOS 和PDOS;(b) 初 始 LixMn0.5Ge0.5SiO3.5S0.5 (x=0,1,2) 中 Mn 和Ge 的PDOS;(c) 位置交换LixMn0.5Ge0.5SiO3.5S0.5 (x=0,1,2)的TDOS 和PDOS;(d) Mn 和Ge 在位置交换 LixMn0.5Ge0.5SiO3.5S0.5(x=0,1,2) 中的PDOSFig.5.(a) TDOS and PDOS of initial LixMn0.5Ge0.5SiO3.5S0.5 (x=0,1,2);(b) PDOS of Mn and Ge in initial LixMn0.5Ge0.5SiO3.5S0.5(x=0,1,2);(c) TDOS and PDOS of site exchange LixMn0.5Ge0.5SiO3.5S0.5 (x=0,1,2);(d) PDOS of Mn and Ge in site exchange LixMn0.5Ge0.5SiO3.5S0.5 (x=0,1,2).

由表5 和图5(a),(b)可以看出,在初始LiMn0.5Ge0.5SiO3.5S0.5体系中,Ge 离子4s 轨道的占据态变为未占据态,而Mn 离子的磁矩和态密度却没有发生太大的变化,说明在一次脱锂时,主要的电荷补偿由Ge 离子提供,且其价态从+2 变为+4.初始Mn0.5Ge0.5SiO3.5S0.5体系的Mn,O 和S 离子存在一些未占据态,Mn 离子的磁矩变为3.78µB,表明在完全脱锂过程中,Mn,O 和S 离子提供电子并参与电荷补偿,Mn 离子从+2(3d5) 价变为+(3 +δ)(3d(4—δ)) 价.由表5 和图5(c),(d)可知,在第一次脱锂过程中,位置交换体系的电荷补偿情况与初始体系相同,在位置交换Mn0.5Ge0.5SiO3.5S0.5体系中,Mn 和O 离子在带隙中出现了一些未占据态,同时Mn 离子的磁矩由4.65µB变为3.41µB,表明当Li+完全脱出时,由Mn 和O 离子提供了电荷补偿.综上所述,可以得出Ge—S 共掺杂可以有效提高Li2MnSiO4的导电性.此外,由于Ge 和S 离子在体系脱锂过程中也可以提供部分电荷补偿,从而可以延缓Li2MnSiO4中Jahn-Teller 效应的出现,有利于提高体系结构循环稳定性.

图6 为LixMn0.5Ge0.5SiO3.5F0.5(x=0,1,2)在初始和发生位置交换情况下的TDOS 和PDOS.从图6(a),(c) 可 以看出,Li2Mn0.5Ge0.5SiO3.5F0.5具有半金属性质,因为F—取代O2—后,为了维持体系的正负电荷平衡,Ge 离子呈+1 价,因此,价带顶部具有Ge 离子4p 轨道的自旋向上占据状态.结合表5 和图6(a),(b)的分析可知,在初始系统中,当每个单元分子式中脱去一个Li+后,体系具有金属性,且Ge 离子4p 轨道的自旋向上占据态消失,在带隙产生了Ge 离子4s 轨道的一些未占据态,而Mn 离子的磁矩和态密度几乎没有变化,证明电荷补偿主要由Ge 离子提供,Ge 离子从+1(4s24p1) 价升高为+3(4s14p0).随着锂离子完全脱出,Mn0.5Ge0.5SiO3.5F0.5具有0.8 eV 的带隙宽度,且Ge 离子4s 轨道的占据态变为未占据态,同时在费米能级处产生了一些来自Mn 离子3d 轨道的电子自旋态,Mn 离子的磁矩变为3.87µB,表明Ge 和Mn 离子共同参与了电荷补偿,其中Ge 离子价态为+4(4s0),Mn 离子从+2(3d5) 变为+3(3d4).

图6 (a) 初 始LixMn0.5Ge0.5SiO3.5F0.5 (x=0,1,2)的TDOS 和PDOS;(b) 初 始 LixMn0.5Ge0.5SiO3.5F0.5 (x=0,1,2) 中Mn 和Ge 的 PDOS;(c) 位置交换LixMn0.5Ge0.5SiO3.5F0.5 (x=0,1,2)的TDOS 和PDOS;(d) 位置交换LixMn0.5Ge0.5SiO3.5F0.5 (x=0,1,2) 中的Mn 和Ge 的PDOSFig.6.(a) TDOS and PDOS of initial LixMn0.5Ge0.5SiO3.5F0.5 (x=0,1,2);(b) PDOS of Mn and Ge in initial LixMn0.5Ge0.5SiO3.5F0.5(x=0,1,2);(c) TDOS and PDOS of site exchange LixMn0.5Ge0.5SiO3.5F0.5 (x=0,1,2);(d) PDOS of Mn and Ge in site exchange LixMn0.5Ge0.5SiO3.5F0.5 (x=0,1,2).

从表5 和图6(c),(d)的分析可知,在位置交换体系中,随着锂离子的逐渐脱出,带隙值也在逐渐增大,LiMn0.5Ge0.5SiO3.5F0.5和Mn0.5Ge0.5SiO3.5F0.5的带隙分别为0.53 和1.56 eV.在LiMn0.5Ge0.5SiO3.5F0.5体系中,Ge 离子4p 的自旋向上占据态消失,同时Mn 离子3d 轨道和Ge 离子4s 轨道存在一些自旋向上未占据态,Mn 离子的磁矩从4.65µB减少到4.17µB,表明在第一次脱去Li+的过程中,Ge 和Mn 离子共同提供了电荷补偿,如Mn 离子从+2(3d5) 价变为 +(2+α)(3d(5—α)),Ge 离子从+1价变为 +(2+β).在Mn0.5Ge0.5SiO3.5F0.5体系中,Ge 离子4s 轨道的占据态消失,而Mn 离子的未占据态增加,Mn 离子的磁矩为3.98µB,说明在完全脱去Li+的过程中,仍然是由Ge 和Mn 离子提供了电荷补偿.综上所述可知,Ge-F 共掺杂Li2MnSiO4具有良好的导电性.此外,Ge-F 共掺杂可以延缓Li2MnSiO4中Jahn-Teller 效应的发生,这是由于F—取代O2—产生的多余电子和Ge 离子容易氧化成更高价态联合作用的结果.

图7 为LixFe0.5Ge0.5SiO3.5S0.5(x=0,1,2)的初始和发生位置交换结构体系的TDOS 和PDOS.从图7(a),(c)可以看出,Li2Fe0.5Ge0.5SiO3.5S0.5的禁带宽度为2.22 eV,具有半导体特性.随着每个单元公式中第一个锂离子的脱去,体系的带隙值减小,初始和发生位置交换的LiFe0.5Ge0.5SiO3.5S0.5带隙值分别为0.93 和1.47 eV.

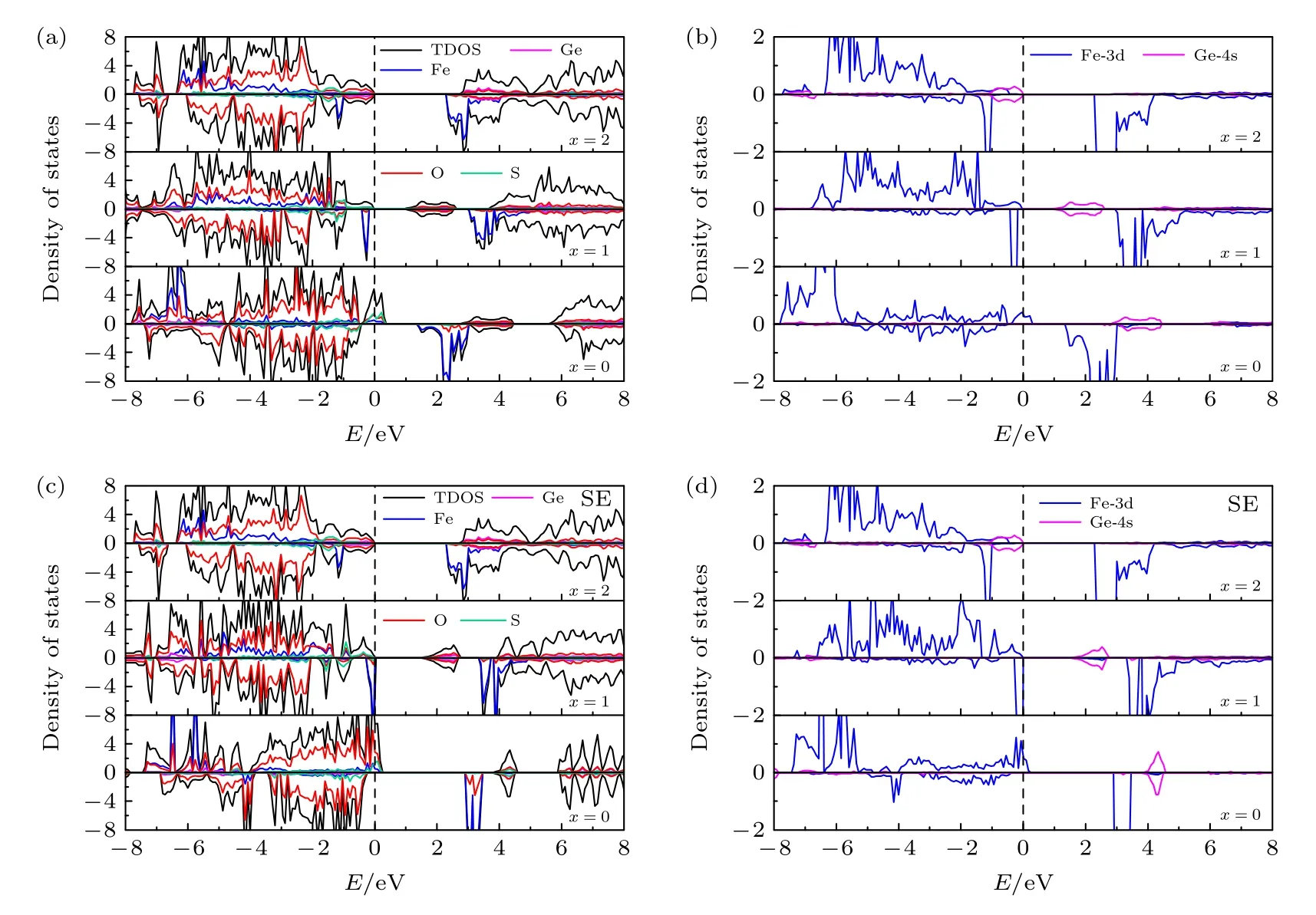
图7 (a) 初始LixFe0.5Ge0.5SiO3.5S0.5 (x=0,1,2)的TDOS 和PDOS;(b) 初始 LixFe0.5Ge0.5SiO3.5S0.5 (x=0,1,2) 中Fe 和Ge 的PDOS;(c) 位置交 换LixFe0.5Ge0.5SiO3.5S0.5 (x=0,1,2)的TDOS 和PDOS;(d) 位置交 换LixFe0.5Ge0.5SiO3.5S0.5 (x=0,1,2)中Fe 和Ge 的 PDOSFig.7.(a) TDOS and PDOS of initial LixFe0.5Ge0.5SiO3.5S0.5 (x=0,1,2);(b) PDOS of Fe and Ge in initial LixFe0.5Ge0.5SiO3.5S0.5 (x=0,1,2);(c) TDOS and PDOS of site exchange LixFe0.5Ge0.5SiO3.5S0.5 (x=0,1,2);(d) PDOS of Fe and Ge in site exchange LixFe0.5Ge0.5SiO3.5S0.5 (x=0,1,2).

从表5 和图7(a),(b)可以看出,当单位分子式中脱出1 个锂离子后,Ge 离子 4s 轨道的占据态变为未占据态,而Fe 离子的磁矩和态密度变化不大,表明Ge 离子为系统提供了电荷补偿.随着锂离子的完全脱出,Fe,S,O 离子存在一些未占据态,Fe 离子的自旋向下占据态消失,且Fe 离子的磁矩为4.02µB,说明Fe,S 和O 离子参与了电荷补偿.由表5 和图7(c),(d)可知,位置交换体系中的电荷补偿与初始体系相似,揭示了Li 和Fe 的位置交换对体系的电子结构几乎没有影响.从以上分析可知,Ge—S 共掺杂可以提高Li2FeSiO4的电导率,同时由于Ge 和S 离子可以代替Fe 离子提供部分电荷补偿,有利于促进体系脱出更多的锂离子.

图8 分别给出了LixFe0.5Ge0.5SiO3.5F0.5(x=0,1,2) 初始和发生位置交换结构体系的TDOS和PDOS.从图8 可以看出,Ge 离子4p 轨道的态密度存在于带隙中并跨越费米能级,导致Li2Fe0.5Ge0.5SiO3.5F0.5具有金属性质,因为当F 离子取代O 离子时,为了维持体系的电荷平衡,Ge 离子为+1 价.因此,Ge 离子4p 轨道的态密度存在于带隙中并跨越费米能级.随着Li+的脱去,带隙趋于增大.初始LiFe0.5Ge0.5SiO3.5F0.5和Fe0.5Ge0.5SiO3.5F0.5的带隙分别为1.12 和2.04 eV,发生位置交换的LiFe0.5Ge0.5SiO3.5F0.5和Fe0.5Ge0.5SiO3.5F0.5带隙分别为1.29 和2.60 eV.

从表5 和图8(a),(b)可以看出,在LiFe0.5Ge0.5SiO3.5F0.5体系中Fe 离子3d 轨道的自旋向下占据态和Ge 离子4p 轨道的占据态消失了,此外,Fe 离子的磁矩从3.73µB变为4.23µB,说明当每单位化学式中脱出一个Li+时,Fe 和Ge 离子共同提供了电荷补偿,即Fe 离子从+2(3d6) 变为+3(3d5),Ge 离子从+1 价变为 +2 价.随着锂离子完全脱出,Ge 离子4s 轨道的占据态变为未占据态,同时Fe 离子的磁矩和态密度变化不大,表明Ge 离子提供了系统所需的电荷补偿,即Ge 离子从+2 价变为 +4 价.从表5 和图8(c),(d)可以看出,位置交换体系的电荷转移与初始系统的电荷转移情况相同,说明位置交换对体系的电子结构影响不大.通过以上分析可知,在完全脱锂时,Ge 离子可提供全部电荷补偿,因此Fe3+不需要被氧化成更高的价态,说明Ge-F 共掺杂不仅提高了Li2FeSiO4的导电性,还有望实现完全脱锂.

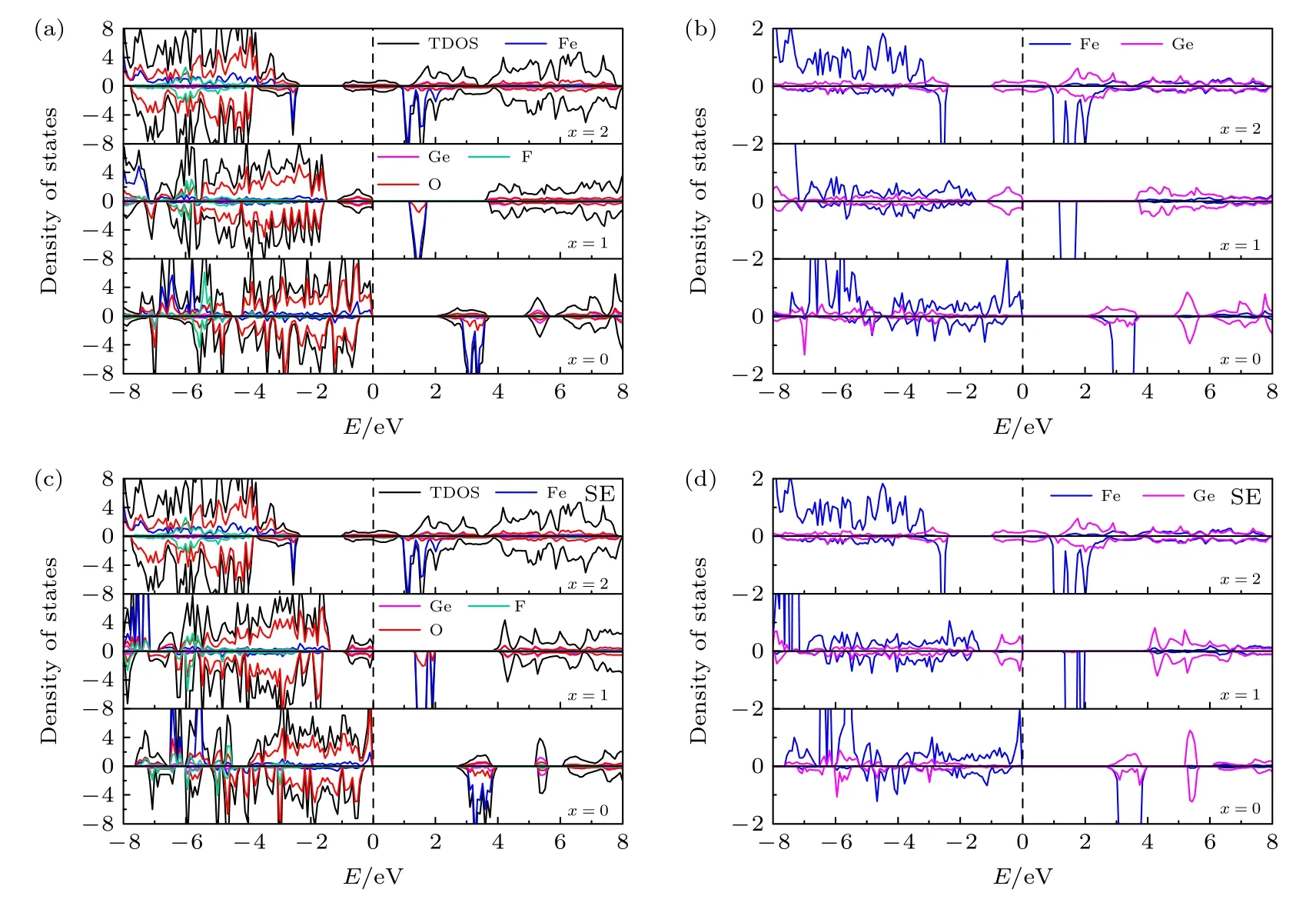
图8 (a) 初始LixFe0.5Ge0.5SiO3.5F0.5 (x=0,1,2)的TDOS 和PDOS;(b) 初始 LixFe0.5Ge0.5SiO3.5F0.5 (x=0,1,2) 中Fe 和Ge 的PDOS;(c) 位置交 换LixFe0.5Ge0.5SiO3.5F0.5 (x=0,1,2)的TDOS 和PDOS;(d) 位置交换LixFe0.5Ge0.5SiO3.5F0.5 (x=0,1,2)中Fe 和Ge 的PDOSFig.8.(a) TDOS and PDOS of initial LixFe0.5Ge0.5SiO3.5F0.5 (x=0,1,2);(b) PDOS of Fe and Ge in initial LixFe0.5Ge0.5SiO3.5F0.5 (x=0,1,2);(c) TDOS and PDOS of site exchange LixFe0.5Ge0.5SiO3.5F0.5 (x=0,1,2);(d) PDOS of Fe and Ge in site exchange LixFe0.5Ge0.5SiO3.5F0.5 (x=0,1,2) .

4 结论

本文系统研究了Li2M0.5Ge0.5SiO3.5R0.5(M=Mn,Fe;R=S,F)的结构循环稳定性和电化学性.结果表明,Li2M0.5Ge0.5SiO3.5R0.5(M=Mn,Fe;R=S,F)体系在脱锂过程中会发生Li 和M位置交换,高模量比、低的杨氏模量和德拜温度表明共掺杂体系具有良好的韧性,且在掺杂体系中Li+更易于迁移.同时位置交换体系在整个脱锂过程中的体积变化更加稳定,尤其是Li2Mn0.5Ge0.5SiO3.5S0.5的体积变化非常小,表现出良好的结构循环稳定性.此外,Ge-S(F)共掺杂均有效降低了Li2MSiO4(M=Mn,Fe)体系中Li+在脱出过程中的理论平均脱嵌电压,有利于锂离子的脱出.态密度图结果表明Ge-S(F)共掺杂有效提高了Li2MSiO4(M=Mn,Fe)的导电性,结合原子磁矩结果分析发现,对于Li2MnSiO4体系,Ge-S(F)的共掺杂可以延缓体系中Jahn-Teller 效应的出现,有利于提高Li2MnSiO4的结构循环稳定性.对于Li2FeSiO4体系,Ge-S(F)共掺杂有利于Li2FeSiO4体系脱去更多的Li+,特别是Ge-F 共掺杂体系可望实现完全脱锂.