基于原位成像技术的同步频率比对与密度频移测量*

胡小华 卢晓同 张晓斐 常宏‡

1) (中国科学院空天信息创新研究院,微波器件与系统研究发展中心,北京 100094)

2) (中国科学院国家授时中心,时间频率基准重点实验室,西安 710600)

3) (中国科学院大学,北京 100049)

精密测量囚禁在光晶格里面中性原子间相互作用导致的密度频移在研究多体相互作用和实现高性能光晶格钟等方面有着重要应用.本文利用基于原位成像的同步频率比对技术对光晶格钟的密度频移系数进行了准确的测量.光晶格里面的原子被一束钟激光同时激发,并通过原位成像技术同时且独立地探测光晶格里11 个不相关区域的钟跃迁概率.由于不相关区域里的原子被同时激发,即共模抑制了钟激光的噪声,因此它们间的频率比对稳定度超越了Dick 噪声的限制,并与原子探测噪声极限相符合.得益于光晶格里非均匀的原子数分布和可以忽略的外场梯度,不相关区域间的频率比对结果即为密度频移.通过测量密度频移和格点平均原子数差的关系,获得密度频移系数为—0.101(3) Hz/(atom·site),经过103 s 的测量时间,系统平均密度频移的相对测量不确定度达到了1.5 × 10—17.

1 引言

利用光晶格囚禁并操控超冷中性原子在量子模拟[1]、量子频标[2-8]和精密测量[9,10]等领域有着重要的应用.囚禁在相同格点的原子间的相互作用往往可以通过测量跃迁频率的变化—“密度频移”来获得[10-12].精确测量密度频移对许多应用来说非常重要,例如量子模拟双体[13]或三体相互作用[14]和光晶格钟[2-8].

在光晶格钟平台上,测量碰撞频移的传统方式主要包括自比对技术和两台光晶格钟同步或异步频率比对[15-17].自比对技术通过将钟激光的频率交替锁定到高、低原子密度下的钟跃迁信号上,可以获得密度(或原子数)差对应的频差,进而线性地推断其他密度(或原子数)情况下的密度频移.当拥有两台光晶格钟时,让其中一台光晶格钟原子数保持不变,使另一台钟交替运行在高、低密度状态,两台钟异步或同步频率比对也能获得密度频移系数.自比对技术和两台钟异步比对的稳定度均受限于Dick 噪声[18],而两台钟同步比对的稳定度可以共模抑制钟激光的噪声,实现超越Dick 极限且接近原子探测噪声极限的测量精度,可以大幅度减小达到特定测量精度所需的时间.然而,传统的测量密度频移的技术只能测量系统的平均的密度频移.光晶格里面的实际原子密度分布并不均匀(通常呈高斯分布,由光晶格装载原子前的原子云密度分布决定),原子密度越靠近晶格中心处越大.当有的格点原子数少于2 时,原则上不存在密度频移,但传统的测量方法不具备这样的分辨能力.最近,基于原位成像的同步频率比对技术在光晶格钟里面得到应用[19],并实现了7 × 10—21的测量精度[20],这为测量密度频移提供了新的技术路线.

本文给出一种基于原位成像的密度频移测量技术,通过对光晶格不同区域进行原位成像并以同步频率比对的方式测量不同区域间的频差.由于不同区域的原子数不一致且其他的系统频移均被共模抑制到可以忽略的程度,因此这种同步频率比对获得的频差即为它们密度频移的差异.

2 实验装置

实验装置如图1 所示,经过两级激光冷却后,约有3000 个87Sr 原子被装载到初始阱深为89Erec(Erec为晶格光子反冲能量)的一维水平光晶格中.光晶格由聚焦到1/e2束腰直径为98 µm(瑞利长度为9.27 mm)的入射光与其反射光在磁光阱中心处干涉形成.晶格光的波长约为813.42 nm,即所谓的“魔术波长”[21],此时原子钟跃迁下能级(5s21S0)与上能级(5s5p3P0)将受到相同的晶格光交流斯塔克频移.波长为461 nm 的探测光用于激发基态原子产生荧光信号,其束腰直径为7 mm(约为晶格有效长度0.37 mm 的20 倍),以减小探测光高斯的光强分布光造成的非均匀散射.正常工作时,探测光的光强和持续时间分别为Isat/20 (Isat≈40 mW/cm2为饱和光强)和20 µs,以减小探测光导致原子横向位置扩散(当前探测光参数下原子横向位置扩散距离为0.611 µm)[19].

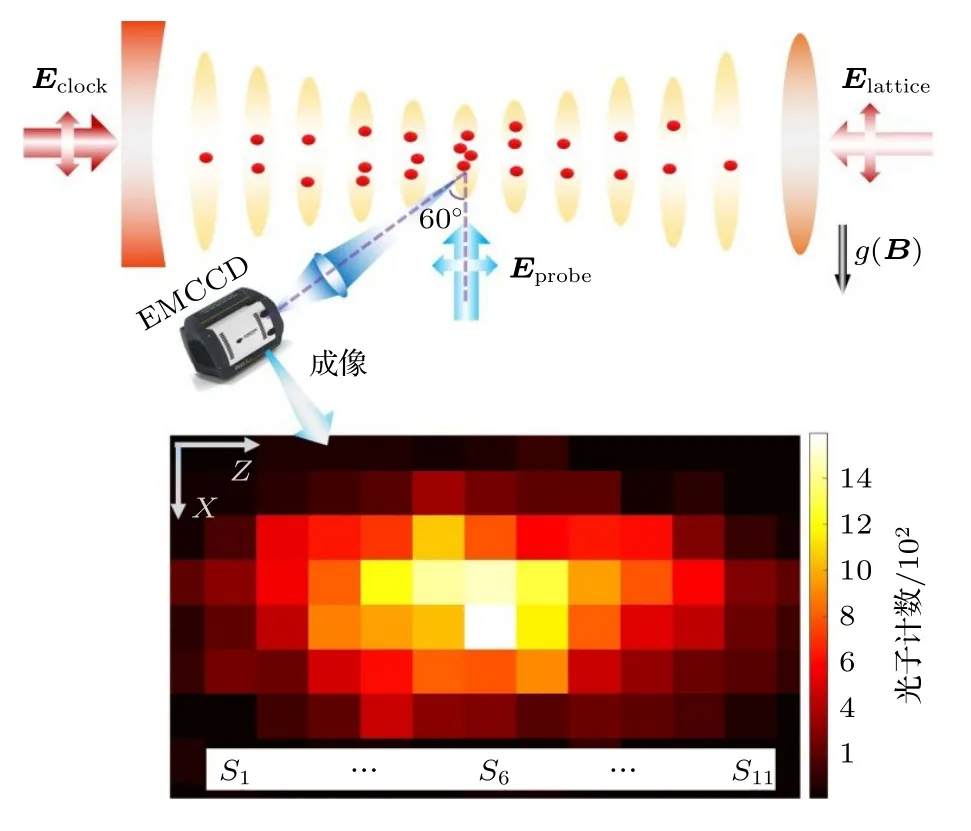
图1 实验装置.晶格光(Elattice)沿水平方向入射,平行于钟激光(Eclock)且垂直于重力和磁场B 方向.电子倍增电荷耦合器件(EMCCD,Andor-897U)用于对光晶格进行原位成像,其探测方向与探测光(Eprobe)的夹角为60°.本实验仅使用下图所示的8(行) × 11(列)的像素区域,这11 列从左到右分别被标记为S1—S11.图片中标注的z 轴平行于晶格光和钟激光,x 轴平行于重力方向Fig.1.Experimental system.The lattice light (Elattice) is incident horizontally,overlapped with the clock laser (Eclock)and perpendicular to the direction of the gravity and magnetic field B.The probe light (Eprobe) is incident horizontally and perpendicular to the lattice light.An electron multiplier charge-coupled device (EMCCD,ANDOR-897U) is used for in situ imaging of the optical lattice,and the angle between the detection direction and the probe light is 60°.This experiment only considers the imaging region of 8 (row) ×11 (column) as shown in the bottom figure.These 11 columns are labeled by S1—S11 from left to right,respectively.The labeled z-axis is parallel to the lattice light and clock laser,and the x-axis is parallel to the gravity direction.

在利用波长为698 nm 的钟激光探测(1S0,F=9/2)→(3P0,F=9/2)钟跃迁信号前,利用一束右(左)旋圆偏振的光将冷原子样品制备到mF=+9/2(或mF=—9/2)的塞曼子能级上,提高钟跃迁谱线的信噪比.此时补偿磁场线圈将水平方向的杂散磁场补偿至零,在竖直(沿重力方向)方向产生一个约50 mGs (1 Gs=10—4T)的磁场.紧接着,在5 ms 内绝热地降低晶格阱深至40Erec,保持10 ms以去除热原子,最后在5 ms 内绝热地将阱深增大至120Erec(此过程伴随着原子数的损耗,使得晶格最终能俘获约1900 个原子).然后,偏置磁场被增加至410 mGs,并利用钟激光进行钟跃迁探测.钟激光的相位被锁定在一个10 cm 长的ULE(超低膨胀玻璃)光学腔上,其频率稳定度为1.2 × 10—15[22].所有的原子均被一束钟激光同时激发,钟跃迁激发率通过“电子搁置法”获得[23],即通过EMCCD 依次记录基态原子、激发态原子和背景噪声对应的光子数.通过测量原子自由下落时间与穿过EMCCD像素点个数的关系,测得EMCCD 的等效像素尺寸为16.65(20) µm,即意味着每个像素点包含82个格点.有效的(原子信号较明显的)成像区域包含8(行) × 11(列)个像素点,将列像素点求和以消除原子径向分布对测量结果的影响.此外,利用光电倍增管对原子总的荧光信号进行收集,并通过标准的伺服算法对钟激光的频率纠正,使钟激光频率与钟跃迁保持共振.

3 实验结果

其中,ν0≈ 4.29 × 1014Hz 为钟跃迁频率,C=0.786 为Ramsey 条纹对比度,Tp=148 ms 为Ramsey 探测第一个π/2 脉冲和自由演化时间之和(两个π/2 脉冲持续时间均为28 ms,自由演化时间为120 ms),TC=1080 ms 为钟探测周期,τ表示平均时间,N表示参与钟跃迁探测的原子数,γ=0.514(34)表示单个原子被检测到的光子数,δdet表示原子数为N1的钟对应的技术噪声.其中,γ的值是通过分别测量平均探测光强为Isat/20 和Isat/4 下的频率比对稳定度并结合(1)式得到的.探测光的功率和频率分别通过液晶功率稳定装置(Thorlabs,NEL03/M,稳定后的功率波动小于0.05%)和原子荧光谱线进行稳定,因此δdet主要由EMCCD 光子计数的散粒噪声决定[25].本实验中δdet小于3.74 × 10—2,其对同步比对稳定度的影响小于1%.

结合原位成像和标准的“电子搁置法”,可以独立且同时地获得S1—S11(或者它们的组合)区域的激发率.频率差信号通过对这些区域的激发率做差并乘以谱线的频率敏感度(πC×Tp)获得[18].这里,仅采用激发率在0.3C—0.7C之间的数据(约占所有数据的50%)来计算频率差[20],以减小Ramsey谱线型造成的测量误差.典型的基于原位成像的同步频率比对稳定度如图2(a)所示,均实现了超越了Dick 噪声限制的稳定度,与(1)式给出的原子探测噪声极限相符合.其中,Dick 噪声限制的稳定度由自比对稳定度除以获得[17].图2(b)展示了图2(a)中进行频率比对的区域的激发率关系.它们均呈现强烈的相关性且数据发散程度随原子数的减少而增加,是受限于原子探测的同步频率比对的典型特征[25].

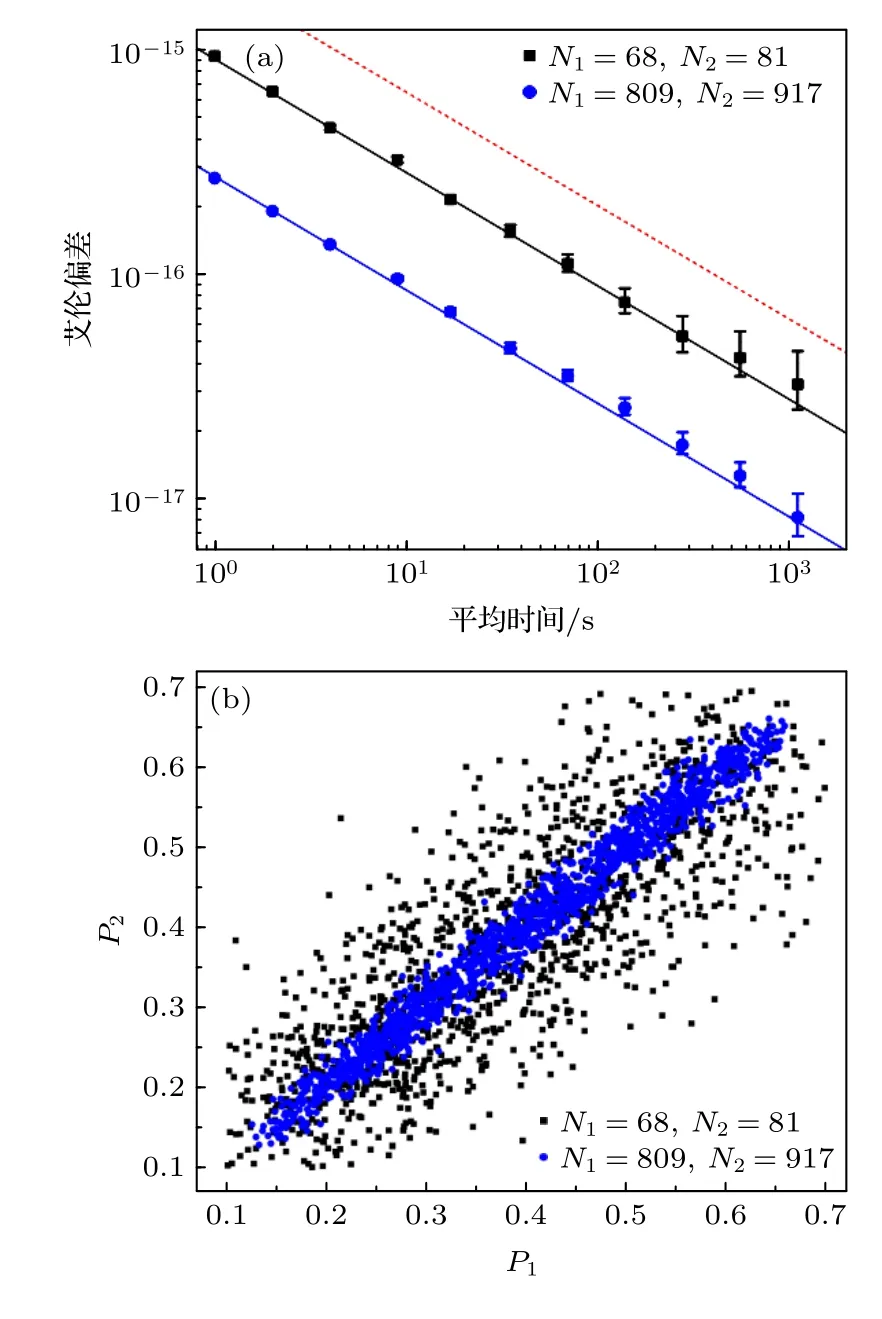
图2 (a) 基于原位成像的同步频率比对稳定度.黑色方点表示S1 (原子数N1=68)和S11(N2=81)间的同步频率比对稳定度(8.9 × 10—16 (τ/s)—0.5),而蓝色圆点表示S1—S5 (N1=809)和S7—S11 (N2=917)两个不同区域间的同步频率对比稳定度(2.7 × 10—16 (τ/s)—0.5).实线表示根据(1)式计算得到的探测噪声限制的稳定度,红色虚线表示Dick 噪声限制的稳定度(2 × 10—15 (τ/s)—0.5).误差棒表示测量结果的1σ 标准差.(b) 对应(a)图中频率比对区域的激发率散点图.P1 和P2 分别表示两个独立区域S1 (或S1—S5)和S11 (或S7—S11)的激发率Fig.2.(a) Stabilities of the in situ synchronous frequency comparison.The black squares indicate the stability of the synchronous frequency comparison between S1 (atom number N1=68) and S11 (N2=81) (8.9 × 10—16 (τ/s)—0.5),and the blue dots are the stability (2.7 × 10—16 (τ/s)—0.5) of the synchronous frequency comparison between S1—S5 (N1=809) and S7—S11 (N2=917).The solid lines are the detection-noise-limited stability calculated by Eq.(1),and the red dotted line represents the Dick-noise-limited stability (2 ×10—15 (τ/s)—0.5).Error bars indicate 1 standard deviation.(b) Scatter plots of excitation fractions of the compared regions shown in (a).P1 and P2 represent the excitation fraction of S1 (or S1—S5) and S11 (or S7—S11),respectively.

得益于晶格微小的空间尺寸,这种基于原位成像的同步频率比对除了可以抑制钟激光的噪声,还能抑制外场梯度等因素导致的频差.通过理想高斯光束计算可知,晶格中心和边缘光强的最大相对变化量小于0.05%.即晶格阱深的相对变化量小于0.07Erec,这种情况下边带可分辨的钟跃迁谱线将测得几乎完全一致的轴向(沿晶格光入射方向)囚禁频率,如图3(a)所示.轴向囚禁频率为75.44 kHz,对应的阱深为120Erec[26].由于实验中晶格光偏离“魔术波长”约10 MHz,通过自比对技术测得的晶格光交流斯塔克系数—2 × 10—5Hz/(Erec× MHz),可以推断S1(S11)与S6间的晶格光交流斯塔克频移最大差异为1.4 × 10—5Hz.将晶格光准确调节到“魔术波长”并增加晶格光的束腰直径,可将这项频移的差异减小至10—7量级甚至更低.同样地,考虑系统中最大温度差异为5 K,线性推断温度梯度为0.008 K/mm,即意味在光晶格空间尺度上(约0.37 mm),黑体辐射频移的差异将小于3 × 10—6Hz.二阶塞曼频移的系数为—0.2338(3) Hz/Gs2[3],通过测量S1与S11区域mF=±9/2 的频率劈裂间距可以获得磁场的梯度为0.05 mGs/mm (频率劈裂差异小于0.05 Hz)[3,20].则二阶塞曼频移的影响小于3.1 × 10—6Hz.每个窗口片经过半小时的紫外灯照射后[27],系统剩余的直流斯塔克频移小于1 × 10—3Hz,则可以线性地推断直流斯塔克频移梯度为1.6 ×10—6Hz/mm,即意味着整个晶格的直流斯塔克频移差异小于6 × 10—7Hz.钟激光交流斯塔克频移为2.7 × 10—3Hz (钟激光的束腰直径约为1 mm,Ramsey 探 测 π/2 脉冲的 耦合强 度约为2π ×10.7 Hz)[28],而S1—S11钟激光光强的变化量小于0.0001%,即钟激光交流斯塔克频移的差异小于2.7 × 10—9Hz.由于本实验密度频移在7 × 10—3Hz以上,比其他频移项导致的频差高出2 个量级以上,因此可以忽略这些外场梯度的影响,同步频率比对获得的频差即为两个相互独立的区域间密度频移的差异.

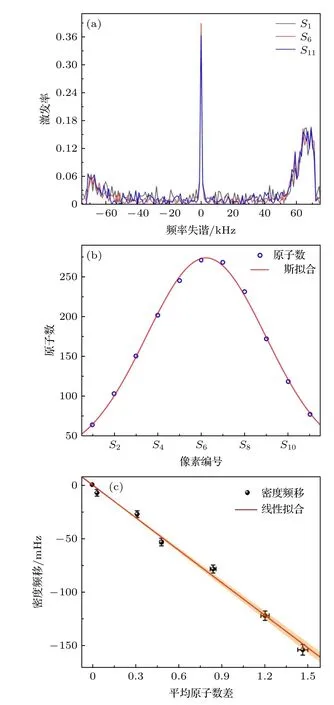
图3 密度频移测量 (a) S1,S6 和S11 区域的边带可分辨的钟跃迁谱线;(b) 原子数分布;(c) 密度频移与格点平均原子数差的关系.红色实线为线性拟合(固定与y 轴的截距为零),橙色区域为拟合线的68%置信区间.误差棒表示测量值的1σ 标准差Fig.3.Measurements of density shift: (a) Sideband-resolved clock transition spectra obtained in S1,S6 and S11,respectively;(b) the distribution of the number of atoms;(c) density shift as a function of atom number difference(ΔN).Red solid line shows the linear fitting (the intercept with the y-axis is fixed as zero),and the orange shade corresponds to 68% confidence intervals of the fitting line.Error bars indicate 1 standard deviation.

原子数在光晶格里的空间分布呈高斯分布,如图3(b)所示,通过恰当选择频率比对的区域可以很方便地对密度频移进行测量.密度频移仅与测量区域的格点平均原子数相关(S1—S11均包含约82 个晶格格点),因此将频率比对区域间的原子数差除以82 以获得格点平均原子数差.由于S6区域的原子数最多,在测量密度频移的时候,将S6作为“参考钟”,然后将其他区域与S6进行同步频率比对,以获得格点平均原子数差与密度频移的关系,如图3(c)所示.通过线性拟合,得到格点平均原子数为1 时的密度频移大小为—0.101(3) Hz (即密度频移系数为—0.101(3) Hz/(atom·site)).由于整个晶格里面的原子数为1900 且包含901 个格点,因此整个晶格的格点平均原子数为2.109,对应的相对密度频移为—4.96(15) × 10—16.这里获得密度频移系数没有考虑EMCCD 有效像素尺寸的测量误差(预计将额外引入1.2%的误差).EMCCD 有效像素的测量误差不会影响系统平均密度频移的评估,因为在计算过程中,密度频移系数和系统平均格点原子数均分别乘以和除以了像素尺寸.

4 结论

本文展示了基于原位成像的同步频率比对技术,频率比对稳定度超越了Dick 极限并与原子探测噪声限制的稳定度相符合.利用原子数在晶格里面呈高斯分布的特点,通过这种同步频率比对技术测量了系统的密度频移,并仅用103s 的测量时间就将系统平均的相对密度频移测量不确定度降低至1.5 × 10—17.增加晶格总的原子数可以提高格点平均原子数的差异,进而提高密度频移系数的测量精度.本文展示的基于原位成像的密度频移测量技术适用于密度频移远大于其他外场影响的情况,通过减小外场梯度或者精确修正每个像素单元外场梯度导致的系统频移将进一步提升这种技术的测量精度和使用范围.实际上,密度频移只发生在那些原子数大于2 的格点,当晶格里面原子数较少时,不可避免地会出现许多原子数少于2 的格点.尽管这些原子数小于2 的格点会增加总的原子,但原则上不会引入密度频移,此时,传统的密度频移测量方法就可能过大地估计系统的密度频移.随着光晶格钟性能的提升,光晶格里面非均匀的原子密度将可能限制光晶格的性能.通过原位成像技术将光晶格划分为多个区域,并精确地修正每个区域的密度频移有助于提高光晶格钟的性能.本文展示的技术可以很容易地应用于其他光晶格钟或某些基于光晶格的物理实验中,将大幅度提高密度频移的测量精度.