自动导航拖拉机的农机具作业精度研究
2022-09-14马志凯赵晓顺赵建国赵树朋于合龙
马志凯,种 坤,赵晓顺,赵建国,赵树朋,于合龙
(1.河北农业大学 机电工程学院,河北 保定 071001;2.吉林农业大学 智慧农业研究院,
吉林 长春 130118)
中国制造2025 计划将智能农业装备列为十大发展领域之一[1],拖拉机自动驾驶系统是当前智能农业装备领域不可或缺的一部分[2-4]。随着高精度差分定位技术的推广,自动驾驶技术在农业作业方面得到了广泛的应用[5-7]。拖拉机的自动导航不仅能提高劳动生产率,解决农村劳动力不足的问题,还有利于精细农业、规范生产等技术的推广[8-10]。拖拉机自动导航是精准农业技术体系中重要基础技术之一。
拖拉机田间作业时作业环境复杂,且拖拉机车况差别大,农机具的作业精度受拖拉机导航精度影响也较大。华南农业大学的赵祚喜教授对拖拉机卫星导航作业精度检验方法进行了研究[9]。华南农业大学的朱金光研究员对水稻插秧机作业效果进行了研究[11]。江苏大学刘继展研究员对农业机械无人驾驶导航参数进行了研究[12]。拖拉机通过三点悬挂拖带农机具作业时,受三点悬挂的影响作业精度会被放大,此时农机具跟踪误差要大于拖拉机本身的跟踪误差,而拖拉机拖带农机具作业的目标是获得农机具按目标路径进行作业,而不是获得拖拉机本身按目标路径进行行驶。因此,研发以农机具作业误差最小为控制目标的导航控制算法尤为重要。
拖拉机的导航控制问题即为拖拉机的路径跟踪问题[11-12]。目前研究拖拉机路径跟踪的诸多问题中常以拖拉机后轴中心的路径跟踪误差最小值为优化目标进行优化控制,未考虑农机具的路径跟踪误差,导致拖拉机带农机具作业时农机具的跟踪误差要大于拖拉机后轴的跟踪误差。针对上述问题本文建立以农机具跟踪误差与拖拉机跟踪误差之和最小为优化目标的拖拉机模型预测控制算法,并通过试验验证了此算法能有效提高农机具的作业精度。
1 拖拉机动力学模型
具有阿克曼转向的轮式车辆在无障碍物的X-Y欧式空间中可以到达任意的位置和姿态,意味着该类车辆拥有二自由度[14-15]。但是实际中该拖拉机在车辆坐标系XV-OV-YV中,由于其机械结构的限制,不可侧向移动。所以该类车辆的运动自由度数大于其动作控制量个数。如图1(A)所示,记大地坐标系下拖拉机后轴中心坐标为(xr,yr),拖拉机前轴中心坐标为(xf,yf),拖拉机前轮转角为α,拖拉机航向为φ,后轴中心速度为vr,拖拉机轴距为D坐标为(xj,yj),机具中心与后轴中心距离为L,拖拉机横摆角速度为ω。
后轴中心处的速度表示为:

前后轮运动学约束表示为:
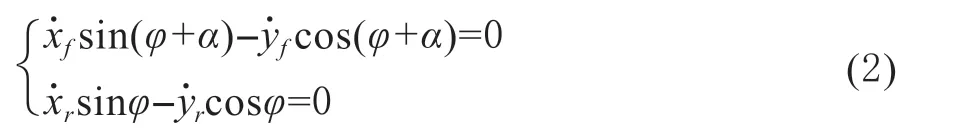
由式(1)和式(2)可得:

根据前后轮几何关系可得:

将式(3)和式(4)带入式(2)可得:

同时拖拉机转弯的几何关系可得:

根据机具与后轴几何关系可得:

因此拖拉机运动学模型为:
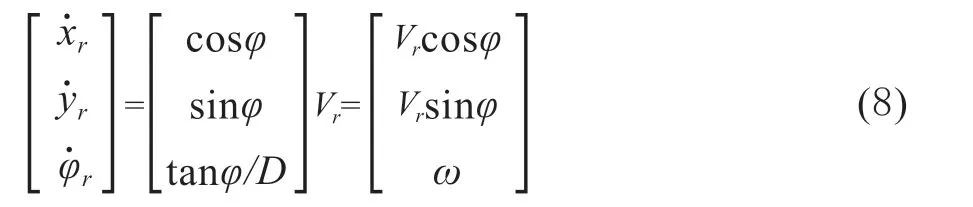
其中状态量为X=[xr ,yr ,φ]T,控制量为u=[vr ,w]T。
式(8)所示为包含农机具的拖拉机系统运动学模型,在拖拉机路径跟踪问题中,应考虑道路因素的影响,因此需要根据拖拉机位置与参考路径计算路径跟踪误差。
目前拖拉机路径导航主要以直线路径跟随为主,因此需构建直线形式的离散路点参考路径。式y=p(x)

在拖拉机坐标系下,定义路径跟踪误差为拖拉机后轴中心位置与参考线之间的横向误差e1两后轴中心位置与参考线之间的航向误差e2置中心位置与参考线之间的横向误差e3,见图1(B)所示。则路径跟踪误差由式(10)表示:
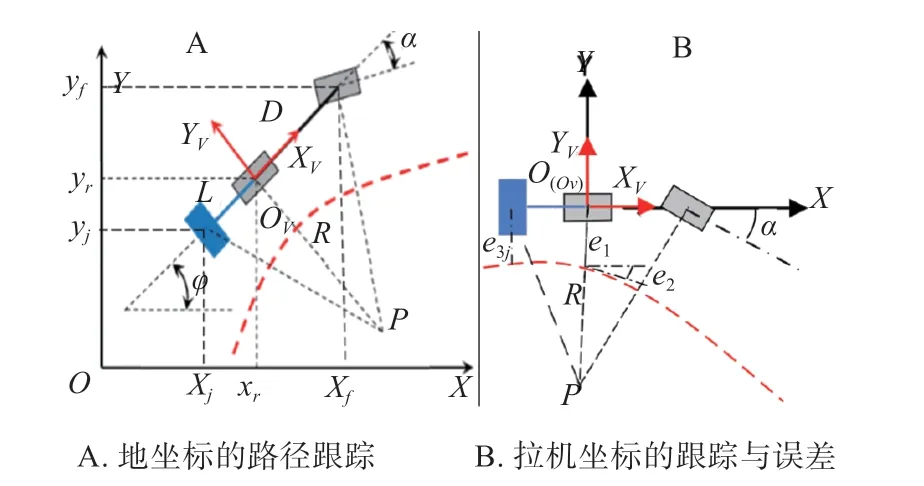
图1 拖拉机路径跟踪图Fig.1 Tractor path tracking
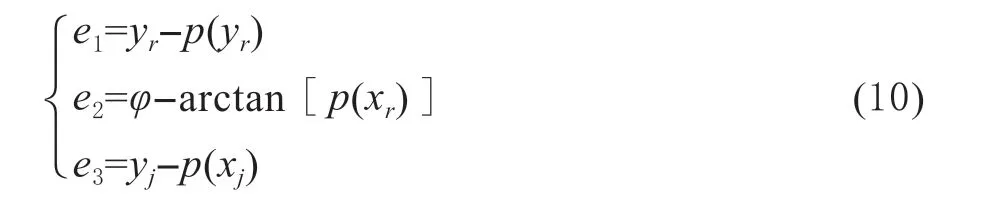
2 模型预测控制问题构建
按照拖拉机位置及农机具与期望路径误差最小,将拖拉机路径跟踪问题构建为模型预测控制问题,由(11)式描述,其中T为测时域,p(x)为拖拉机参考路径。
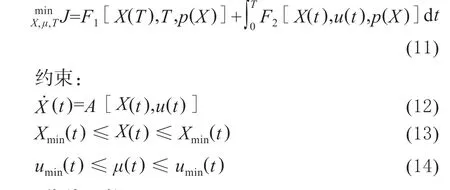
2.1 代价函数
式(11)表示了模型预测控制问题的评价指标,设定为代价函数J,如式(15)所示。
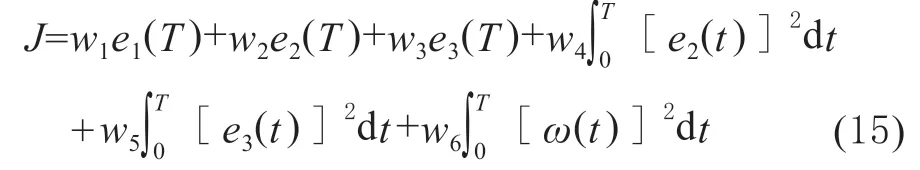
其中,w1至w6为系数,e1(T),e2(T),e3(T)分别表示预测时域末端时刻的路径跟踪误差,这部分代价函数的主要目的是为了防止模型预测控制问题在求解时发散,期望车辆在预测时域时刻保持在路径上。代价函数中的积分项代表了拖拉机行驶过程中,路径跟踪位置误差与航向误差,同时w6所表示的指标期望拖拉机以尽可能稳定的横摆角速度行进。
2.2 约束条件
式(12)所示为拖拉机系统状态约束条件,由式(8)表示。式(13)为拖拉机状态量约束,由于拖拉机位置与航向在路径跟踪问题中为相互独立的状态量,不受环境条件约束,因此没有约束上下限,即:
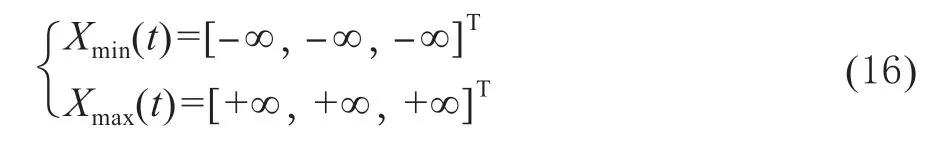
式(14)为拖拉机控制量约束,拖拉机在作业时,通常以固定车速行进,同时设定拖拉机横摆角速度上下限,即:

其中vt表示设定的固定车速,ωmax为设定的横摆角速度上限。
2.3 时变系统离散化
本文使用非线性求解器IPOPT 对模型预测控制问题进行求解,IPOPT 使用内点法求解非线性问题的局部最优解。该方法将等式与不等式约束分解为一系列等式约束,然后用迭代的方法求解只含有等式约束的非线性问题。为保证求解结果的准确性,使用精确的雅可比矩阵与海森矩阵求解。在使用IPOPT 非线性求解器时,需要将时变系统进行离散化,由式(8)可得:
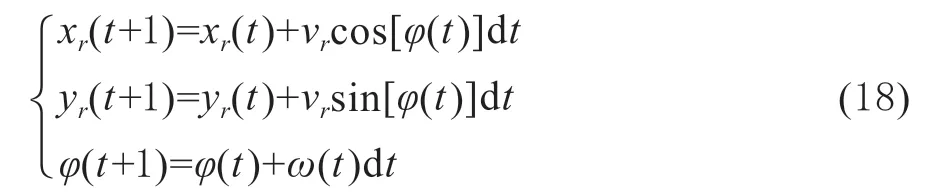
由式(10)可得:
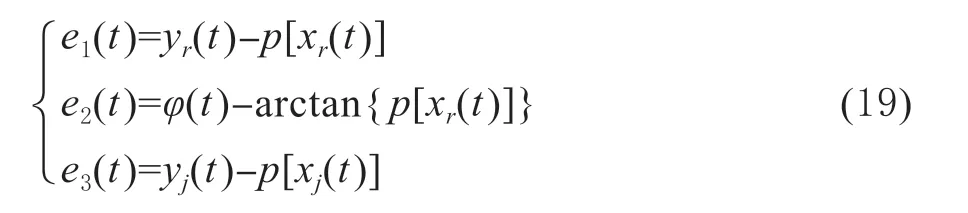
式(18)和式(19)所示为拖拉机路径跟踪系统的离散表达形式。
3 算法可行性验证
3.1 试验构建
为验证该算法路径跟踪保持的可行性,搭建实物进行试验。
定位系统采用基于北斗的ublox 模块自行开发的双天线RTK 高精定位系统。该定位系统通过连接千寻定位服务器获取RTK 定位信号,绝对定位精度可以达到±2 cm。主控制器为基于ARM Cortex®-M 核的32 位处理器M481LIDAE 开发的嵌入式控制器。在该控制器中实现轨迹跟踪,控制周期为100 ms。
转向电机采用满足控制要求北京涛峰科技有限公司生产的直驱电机,该电机最大扭矩可达10 N·m,额定工作转速100 r/min,位置控制精度0.1°。
选取磨损比较严重,转向系统左右两侧空行程较大,且不对称的雷沃欧豹950 为试验车。试验搭建车辆如图2 所示。

图2 试验拖拉机雷沃950Fig.2 Experimental tractor Revo 950
3.2 算法可行性试验
为验证此算法对拖拉机直线跟踪保持的可行性,选取代价函数的系数w1=0.02,w2=0.02,w3=0.02,w4=1,w5=0,w6=0.4 即算法对拖拉机路径跟踪控制的可行性验证。试验包括拖拉机起步入轨,倒车入轨、单次换挡、多次换档试验。试验的数据采样周期为0.05 s。
起步入轨是指拖拉机后轴中心点偏离跟踪轨迹一定距离起步跟踪预定轨迹行驶。倒车入轨是指拖拉机在轨迹上倒车起步跟踪预定轨迹行驶。试验测得拖拉机后轴中心点横向误差、速度及拖拉机航向误差如图3 所示。
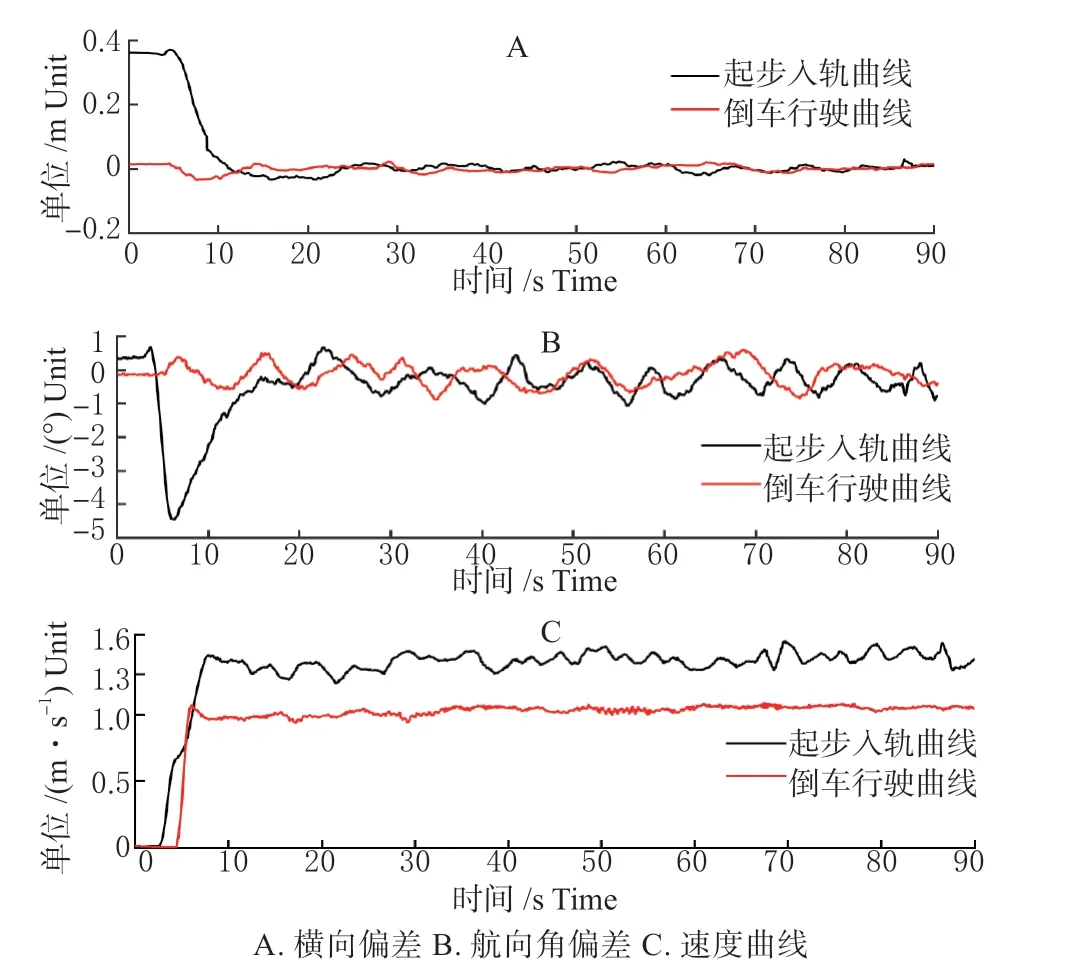
图3 入轨试验Fig3 Test of enter an orbit
图3(A)中知拖拉机偏离预定直线轨迹0.5 m处起步入轨,图3(C)知车辆行驶4.5 s,行驶约为5 m,以1.3 m/s 左右的速度进入预设轨道,图3(A)拖拉机偏离预定直线轨迹0.025 m 起步倒车跟踪预定轨迹行驶,图3(C)知车辆行驶2.5 s,行驶约为3 m,以1.02 m/s 左右的速度进入预设轨道。上述2种工况拖拉机入轨后,能稳定地跟踪直线路径行驶,同时横向最大偏差小于5 cm,航向角最大偏差小于1°。上述试验表明此算法能使拖拉机有效跟随直线路径。
单次换挡是指拖拉机行驶过程中换入相邻挡位。多次换挡是指拖拉机在行驶过程中多次换入相邻挡位。试验验测的拖拉机后轴中心点横向误差、速度及拖拉机航向误差如图4 所示。
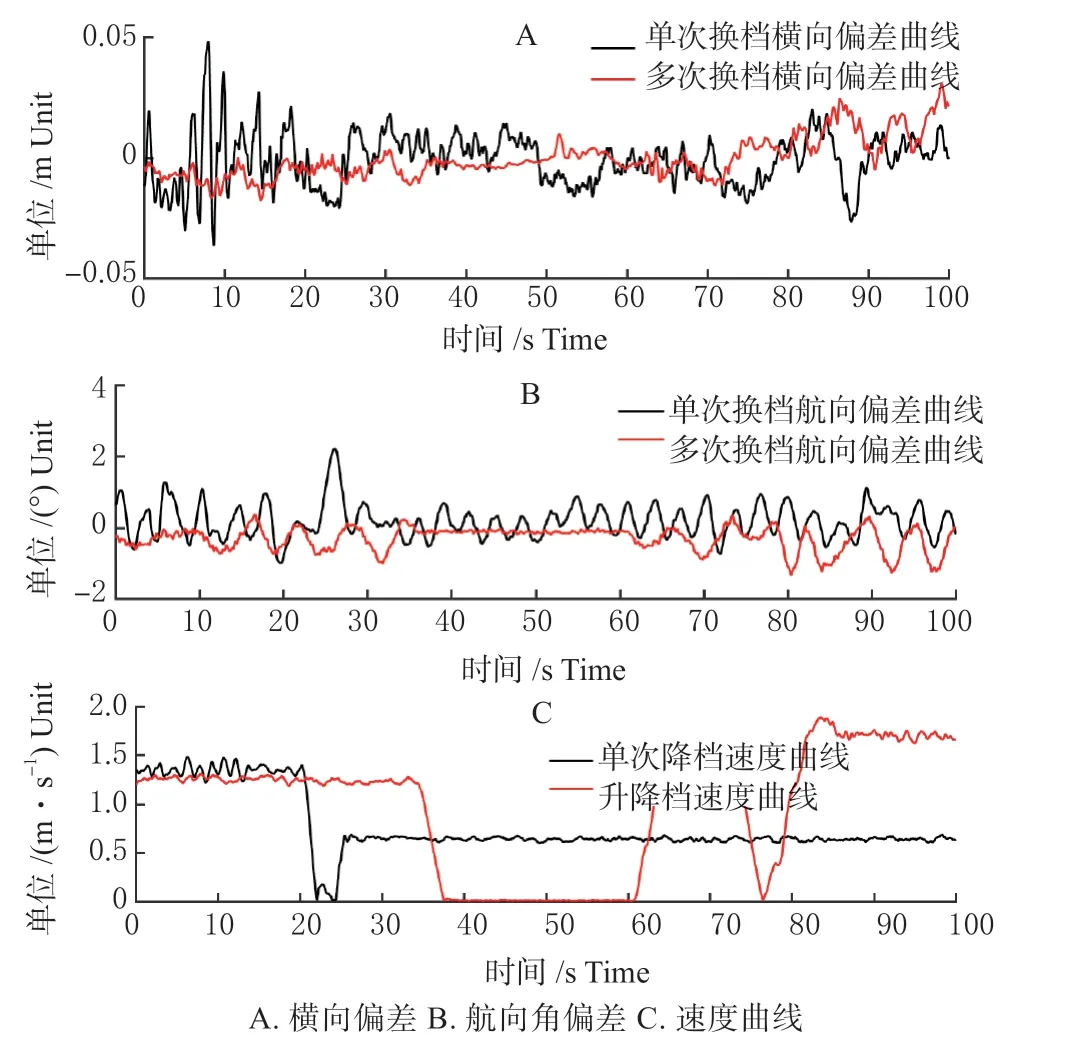
图4 换挡试验Fig.4 Experiment of shift gears
图4(A)知换挡过程横向误差变化较小,受工况、速度影响多次换挡的横向偏差优于单次换挡,受速度影响多次换挡的后期横向偏差变差。图4(A)知单次换挡航向角在换挡时受速度波动影响出现较大航向角偏差,但仍保持了较高的跟随精度。图4(C)知单次换挡过程中由于动力中断时间过长,导致拖拉机速度出现大幅度下降,直至速度降为0 m/s,同时在换挡过程中23 s 处由于操作失误导致1 次速度抖动,引起了航向角偏差增大,随后仍能保持较高跟随效果。多次换挡中停车后再次挂挡起步且经过1 次高档切换,横向位置偏差变化较小,控制精度未受到影响。从上述表述知此算法能适应不同状态的换挡过程。
起步入轨,倒车行驶、单次换挡、多次换档试验表面,本算法能有效实现拖拉机直线路径跟随,并适应拖拉机不同复杂工况的使用要求。
4 拖拉机带机具作业试验与分析
拖拉机带农机具作业时农机具受三点悬挂结构及作业环境的影响,农机具行驶轨迹与拖拉机的行驶轨迹并不重合。为验证此算法对农机具直线跟踪的影响,进行拖拉机带机具作业试验。
4.1 拖拉机带机具作业试验
使用上述拖拉机拖带河北双天农机有限公司生产的1.5 m 旋耕机作业测试,其中旋耕深度是130 mm。选取w1=0.02,w2=0.02,w3=0.02,w4=1,w5=0,w6=0.4算法不带机具误差测得农机具中心点的横向误差,速度及拖拉机航向误差数据如图5 所示。取w1=0.02,w2=0.02,w3=0.02,w4=1,w5=1,w6=0.4 算法带机具误差测得农机具中心点的横向误差,速度及拖拉机航向误差数据如图6 所示。图5、6 中低速为0.4 m/s,中速为1.5 m/s,高速3.3 m/s。
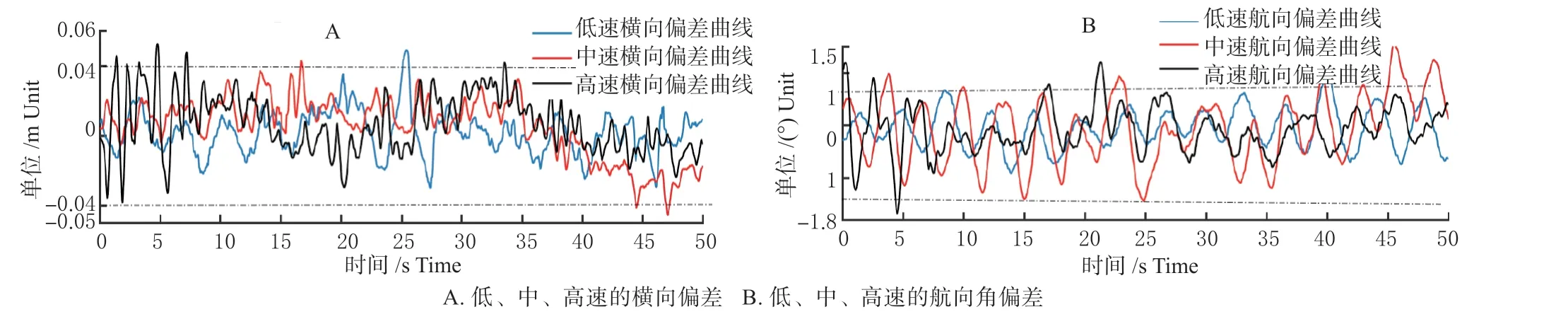
图5 算法不带机具误差的作业试验Fig.5 Work test without considering agricultural machinery errors
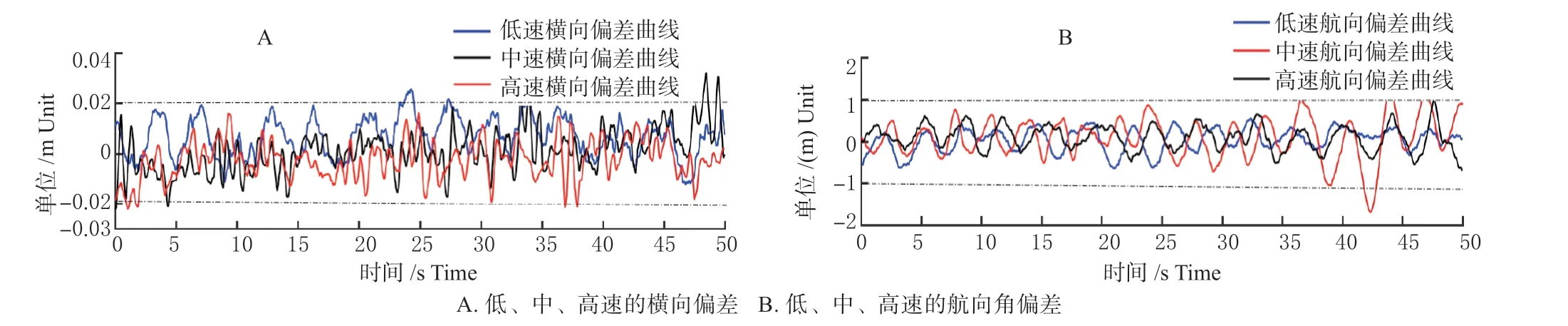
图6 算法带机具误差的作业试验Fig.6 Work test with considering agricultural machinery errors
4.2 试验结果分析
由图5 知,该算法在不考虑机具误差进行拖带旋耕机低速作业时,横向偏差最大值在25~26 s 之间为0.048 6 m,航向角偏差小于1°;中速作业时,最大横向偏差在47~48 s 之间为0.045 8 m,最大航向角偏差在56 s 处为1.55°,高速作业时,最大横向偏差在4~5 s 之间为0.052 6 m,此时航向角偏差达到了负向最大值1.488 5°,10 s 以后横向偏差、航向角偏差都趋于稳定。此时,拖拉机以中速与高速、低速作业行时横向偏差前者优于后两者,以低速行驶时横向位置偏差最大。
由图6 知,该算法考虑机具误差进行拖带旋耕机低速作业时,横向误差基本上±0.02 m 之间,在23~25 s 之间的最大偏差为0.023 m,横向角偏差变化幅度较小,基本上处于±0.8°之间,中速作业时,最大横向偏差在36 ~38 s 之间为0.024 6 m,航向角偏差受工况影响在42~44 s 之间,出现了大于1°的航向波动,波动时间非常短且只出现了1次,可视为偶然误差。高速作业时,最大横向偏差在47~48 s 之间为0.032 m,横向偏差波动具有随机性,航向偏差波动较稳定。此时拖拉机高速、中速、低速作业行时横向偏差,航向偏差有所差别,但相差较小,速度对其影响不明显。
由图5、6 知,从改善程度看,横向位置偏差比航向角偏差更为明显。不同作业速度下旋耕机的横向偏差基本在0.02 m 以内,直线跟随能力得到了大幅度提高。具体差异如表1 所示。
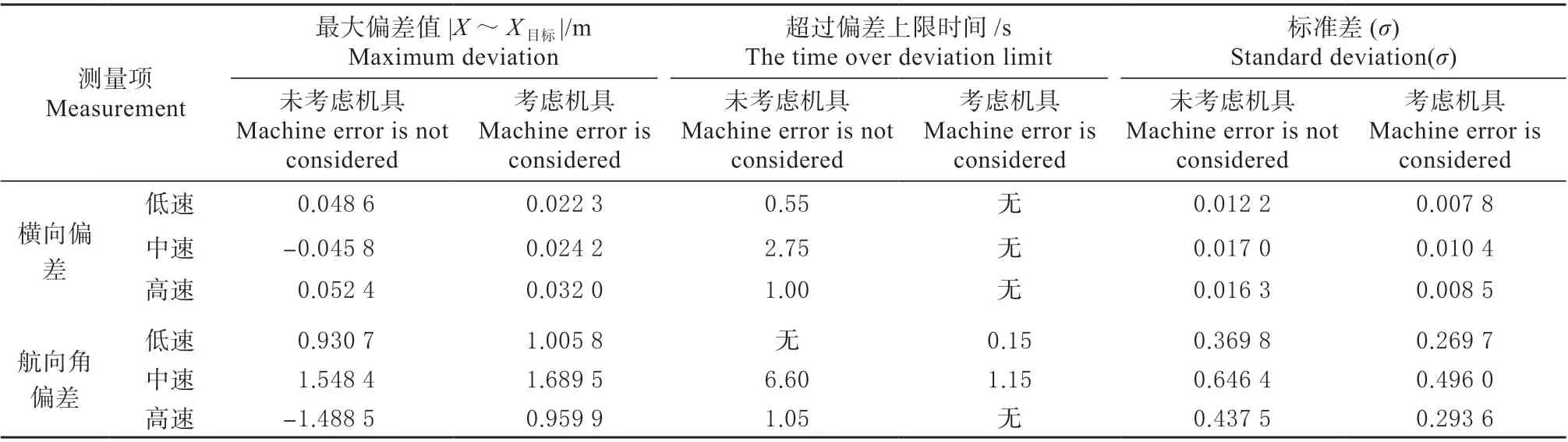
表1 旋耕机作业精度对比表Table 1 Rotary cultivator operation precision comparison table
上述表中可知,该算法考虑农机具误差后,直线保持性能得到提高,最大横向偏差变小,横向最大偏差分别降低了54.11%、45.74%、38.93%,低速与中速航向角最大偏差分别提高了8.06%、9.11%,高速航向角最大偏差降低了35.51%。低速与中速航向角最大偏差角有所增大,但超过1°的时间分别降低了85.06%、82.57%。同时从其标准差看,横向偏差标准差分别降低了36.06%、38.82%、47.85%,航向角偏差标准差分别降低了36.97%、23.26%、32.89%。
从以上数据知,该算法考虑农机具的误差时,农机具的横向偏差得到了极大地改善,且机具航向角的标准差得到了大幅度提高。综上所述,拖拉机拖带农机具作业时采用拖拉机与农机具误差之和最小值为优化目标的模型预测控制算法能够减小农机具的跟踪误差。
5 结论
1.拖拉机模型控制预测算法对拖拉机直线路径跟踪具有良好的可行性。
2.考虑机具误差的拖拉机模型控制预测算法能有效提高拖拉机带农机具作业时农机具的作业精度。试验表明,拖拉机在低、中、高3 种速度带农机具作业时,横向偏差平均降低了42.36 %,横向偏差标准差平均降低了40.91 %,航向角最大偏差平均降低了6.11 %,航向角偏差标准差平均降低了31.04 %。对带机具作业的拖拉机进行直线跟踪作业控制时,在代价函数中增设农机具误差项的预测控制算法能有效改善农机具的作业精度。
