粒子群算法在镁合金3C 产品覆盖件冲压成形优化中的应用

高孝书，曹桐，张 宗

（宁夏职业技术学院 工业工程学院，宁夏 银川 750021）

0 前言

镁合金3C 产品覆盖件冲压成形是材料非线性、几何非线性和边界非线性的成形过程，极易出现冲压开裂和起皱等缺陷，冲压成形工艺的制定及优化成本高、难度大，一直是镁合金3C 产品塑性成形领域的研究热点[1]。

本文基于有限元数值模拟和粒子群优化算法的冲压成形优化方法，引入了非线性自变惯性权值和非线性自变加速因子，对多目标粒子群优化算法进行针对性改进（impoved particleswarmoptimization，IPSO），构建了工艺参数与成形质量之间的数学分析模型，利用IPSO 粒子群优化算法求解数学分析模型，获得了最优冲压成形工艺。

1 改进粒子群优化算法

在非线性大变形的覆盖件冲压成形中，由于非线性约束问题，易导致粒子群优化计算时，求解出局部最优而全局空间非劣的次优解[2]。为了解决此类非最优问题，本文在传统的多目标粒子群优化算法中，针对性地引入了非线性自变惯性权值和非线性自变加速因子。

1.1 非线性自变惯性权值

在多目标粒子群优化算法中，惯性权值ω 是描述各粒子对现速度继承的阈值，是权衡各粒子全局空间搜索能力和局部空间搜索能力的重要平衡参数。当惯性权值ω 较小时，多目标粒子群优化算法的局部空间搜索能力变强；当惯性权值ω 较大时，则多目标粒子群优化算法的全局空间搜索能力变强[3]。

在不同的计算迭代中，采用非线性自变惯性权值ωc要比采用固定惯性权值的寻优效果更好[4]。因此，本文根据非线性大变形覆盖件冲压成形特性，将非线性自变惯性权值ωc与目标函数值相挂钩，在每次迭代计算中，非线性自变惯性权值ωc都会随着目标函数值的不同而自动发生改变，其公式为：

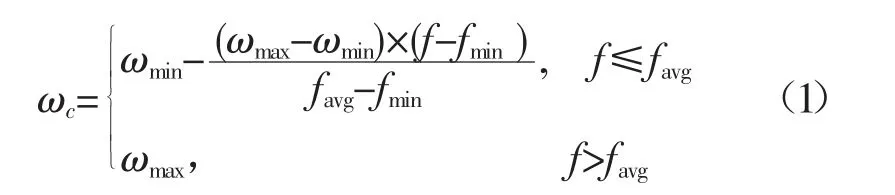
式中：ωmax为惯性权值ω 的最大值；ωmin为惯性权值ω 的最小值；f 为各粒子现速度目标函数值；favg为各粒子目标平均值；fmin为各粒子目标最小值；

1.2 非线性自变加速因子

在多目标粒子群优化算法中，加速因子σ1和σ2是各粒子向群体中优秀粒子靠近的调节因子。根据每次迭代计算中，不断变化的加速因子σ1和σ2的初始值和终了值，而非线性自变的加速因子σ1(t)和σ2(t)，可使各粒子在优化过程中不断增强全局空间搜索能力，最终提升最优解的捕获能力[5]，其公式为：

式中：σ1，s为σ1的初始值；σ1，f为σ1的终了值；σ2，s为σ2的初始值；σ2，f为σ2的终了值；t 为迭代次数；tmax为最大迭代次数。

2 构建算例数学分析模型

本文以某镁合金3C 产品覆盖件的冲压成形为研究对象，该覆盖件的有限元数值模拟三维模型如图1 所示。

图1 覆盖件有限元数值模拟三维模型

2.1 设定分析模型参数

镁合金是世界上最轻的金属结构材料，是3C产品覆盖件的理想选材。室温下镁合金的塑性变形能力差，冲压成形时易发生开裂和起皱缺陷；随着变形温度的升高，镁合金的塑性变形能力增强，特别是在复杂温变条件下，冲压成形性能更好[6]。因此，本文选用板材温度Td和凸模温度Tp作为首要设计变量，再选择对冲压成形影响较大的压边力F和冲压速度S 作为次要设计变量，其他影响因素以设计常量处理。

冲压板材为AZ31B 镁合金，材料性能参数为：板材厚度τ=0.9mm，弹性模量E=44.8GPa，泊松比v=0.35，热膨胀系数α=2.5×10-5℃-1，摩擦系数μ=0.125，板材尺寸为140mm×75mm，板材圆角r=10mm。冲压模具设定为刚体，凸凹模间隙Z=0.99mm，凸模圆角半径Rp=3.5mm，凹模直壁圆角半径Rc=4.2mm，拉延筋阻力R=230N/mm。

2.2 构建目标函数

冲压成形的缺陷主要有开裂、起皱和成形不足等3 类。在镁合金3C 产品覆盖件冲压成形中，成形不足缺陷的影响很小，本文主要考虑开裂缺陷和起皱缺陷。

根据成形极限图FLD（图2），定义开裂和起皱曲线如下：

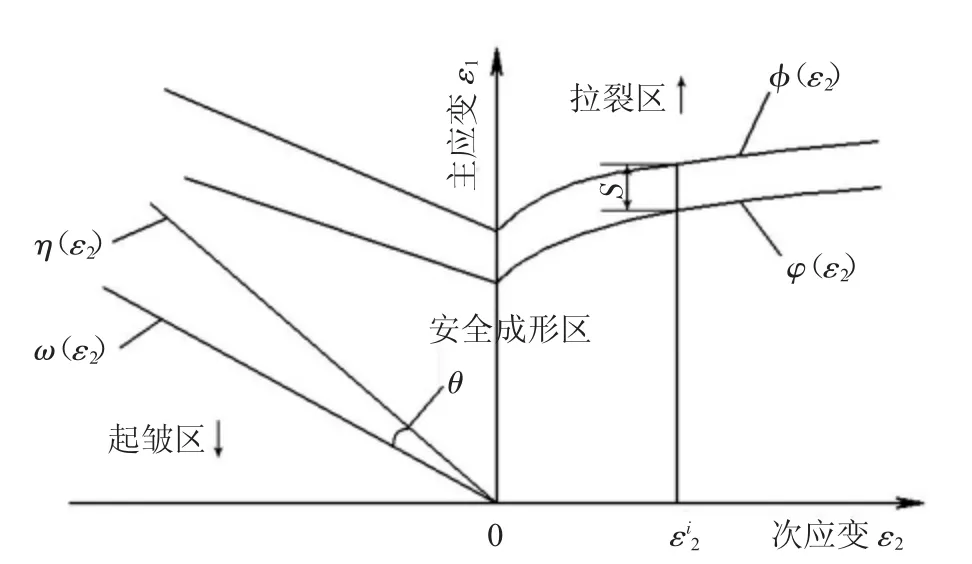
图2 成形极限曲线的定义

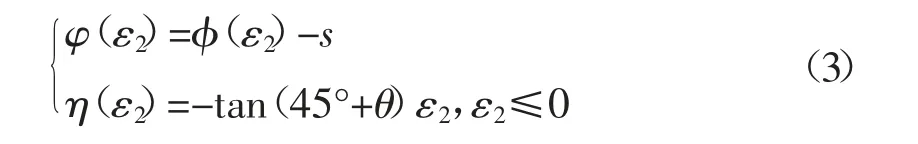
式中：（ε2）为拉裂极限曲线；φ（ε2）为拉裂安全曲线；η（ε2）为起皱安全曲线；ε2为次应变；s 为拉裂安全度；θ 为起皱安全度。

在成形极限图FLD中，距离安全成形区域越远的单元开裂和起皱的危险程度越大[7]，本文以安全距离的指数为权重，构造开裂目标函数Robj和起皱目标函数Wobj如下：

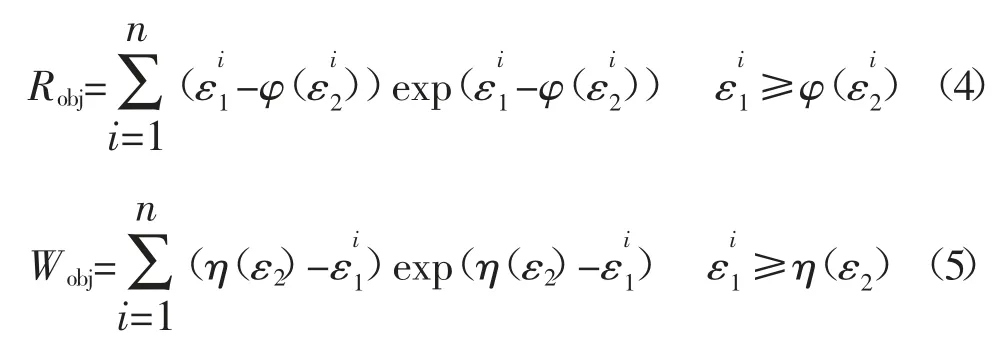
式中：n 为板材单元总数；ε1为主应变；ε2为次应变。

2.3 构建优化模型

在镁合金3C 产品覆盖件的冲压成形中，构建优化数学模型如下：

对板材温度Td、凸模温度Tp、压边力F 和冲压速度S4 个连续的设计变量，以正交试验均匀选取64组样本进行有限元数值模拟计算，其中48 组作为训练样本，24 组作为测试样本，将试验得到的主应变ε1和次应变ε2带入公式（3）～公式（5），即可求解出相应的目标函数值[8]。

3 优化计算与结果分析

3.1 优化计算

设定粒子种群大小为35；终止迭代次数t=200；设定最大惯性权值ωmax=1.2；最小惯性权值ωmin=0.6；加速因子σ1的初始值σ1，s=3；加速因子σ2的初始值σ2，s=0.5；加速因子σ1的终了值σ1，f=0.5；加速因子σ2的终了值σ2，f=3。

利用IPSO 粒子群算法，求得二次多项式响应面数学模型如下：

3.2 结果分析

经过IPSO 粒子群算法优化计算后，运用最小距离选解法，将求得的开裂目标函数Robj值和起皱目标函数Wobj值在空间解集中选取距离最短的最优粒子Pm。Pm对应的工艺参数为：板材温度Td=271.33℃，凸模温度Tp=45.61℃，压边力F=20201.17N，冲压速度S=1.70mm/s。

将IPSO 计算的最优粒子Pm的工艺参数，输入Dynaform 有限元软件进行数值模拟计算，得到的成形极限图FLD，如图3 所示。从图中可以看出，镁合金3C 产品覆盖件的开裂和起皱得到了有效控制，未产生开裂和严重起皱等缺陷，覆盖件冲压成形安全且充分。

图3 最优粒子Pm 的成形极限图FLD

4 结论

本文成功将非线性自变惯性权值和非线性自变加速因子引入到多目标粒子群优化算法中，构建了工艺参数与成形质量之间的数学分析模型。在此基础上，将IPSO 粒子群算法应用于镁合金3C 产品覆盖件冲压成形后，取得了满意的效果。实例证明，IPSO 粒子群算法能有效优化镁合金3C 产品覆盖件冲压成形工艺，显著提升复杂温变条件下覆盖件的冲压成形质量。