基于 LabVIEW 的 2PSK 系统的仿真设计与实现

刘佳明

（南京信息工程大学，江苏南京，210044）

0 引言

数字无线电又称数字频带传输，其任务是在两个或多个点之间，传送经过数字调制的模拟载波信号，是一种广泛应用的通信系统[1]。对数字信号实现调制的最基本方法有3种，分别通过改变载波的幅度、频率和相位来实现。第一种是幅移键控调制，简称ASK，它是通过改变载波的振幅大小来表示信号的；第二种是频移键控调制，简称FSK，它是通过改变载波的频率快慢来表示信号的；第三种相移键控，简称PSK，是通过改变载波的相位来表示信号的。本文中主要对二进制信号的PSK，简称2PSK的调制解调原理进行验证。

本文通过LabVIEW实现对2PSK系统的仿真设计，通过观察2PSK调制解调过程中不同阶段对应信号的波形，可以更好地理解2PSK的原理。

1 2PSK的调制解调原理

■ 1.1 2PSK的调制原理

2PSK是通过改变载波的绝对相位来传递数字信号的。在2PSK系统中，二进制“0”可以设为0相位，也可设为Π相位，二进制“1”也是如此。但是，通常情况下，二进制“0”用初始相位0来表示，“1”用初始相位Π表示[3]。

由此， 2PSK信号的时域表达式为：

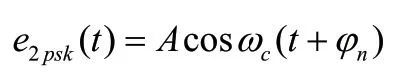
其中φn为第n个符号的绝对相位：

同样，2PSK的时域表达式也可表示为：

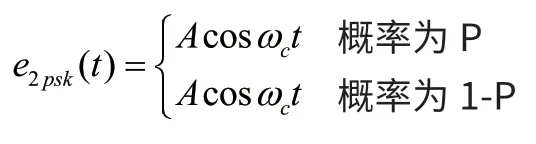
2PSK信号的调制方法分为键控法和模拟调制法两种。

■ 1.2 2PSK的解调原理

2PSK信号的解调通常采用相干解调法。首先将2PSK信号通过一个带通滤波器，过滤掉没有用的噪声信号；再将通过带通滤波器之后得到的信号与相干载波相乘，设“0”用初始相位0来表示，“1”用初始相位Π表示，则0对应的输出信号为正，1对应的输出信号为负；接着通过一个低通滤波器，使得信号中的高频分量被转换为低频分量输出，若2PSK解调中没有了低通滤波器，一个高频的信号在经过抽样判决器抽样时，因为它在一个码元宽度内，零点很多，所以很容易抽样到0点附近的值造成结果的不准确；最后进入抽样判决器，抽样频率与码元速率一致，通过输入定时脉冲的方式，做到位同步，利用阈值电压是否大于零判别，得到最后的解调输出信号。

2 2PSK系统的LabVIEW设计与实现

在构建2PSK系统时，本文采用模拟调制法和相干解调法。设“0”用初始相位Π来表示，“1”用初始相位0来表示。仿真流程如下：首先产生一个与载波速率一致且能发送任意序列的输入序列，通过对它的极性转换产生负的输入序列，再将两个序列相加后得到双极性序列。将双极性序列与载波相乘后得到2PSK信号。本文中假设2PSK经过的信道为理想信道，所以不必再加入带通滤波器滤出噪声，直接将得到的2PSK信号与相干载波相乘后经过低通滤波器，将高频分量转换为低频分量输出，最后经过抽样判决器来还原基带信号。抽样判决器是通过for循环判断每个码元中间时刻的抽样值是否大于0，来判断每个码元是0还是1来实现的。

本文中运用LabVIEW作为仿真软件。LabVIEW是一个图形化的软件，利于理解。它通过编写程序流程图，通过它们之间的连线关系可以实现对一个通信系统的仿真，易于理解和上手。在利用LabVIEW进行仿真设计的时候，要善于应用模块化的思想，将一个复杂的仿真问题划分为若干子模块进行解决，最后再将它们整合起来。

■ 2.1 产生序列.vi的设计

由于LabVIEW自带仿真信号中的方波只能发送周期的信号，即只能发送“0”和“1”交替的信号，不能发送类似于“0111001”的这种随机序列，可是我们需要构建出的系统要能发送任意序列。首先，在前面板中创建输入序列、码速率RS、采样率Fs，3个数值输入控件以及一个波形图输出控件，输出输入序列的波形。先通过数组大小控件判断输入数组的长度，作为第一个for循环的循环次数，再利用索引数组控件判断第i次循环时，在该数组相应的i位置上的数为1还是0。因为在产生输入序列时，需要控制输入序列产生的速度与载波的速度一致。所以，第二个for循环的目的是将数组按固定的速率输出。可是由于输出的数组为二维数组，所以此时需要利用事先完成的二维数组转一维数组控件将输出的二维数组转成一维数组输出，得到最后的输入序列。

■ 2.2 2PSK系统调制部分设计

首先在前面板创建6个输入控件，分别改变输入序列、采样点数、采样率、码速率、初始相位、载频。除此之外建立输入序列波形、载波波形，2PSK波形、2PSK频谱4个波形图输出控件和一个码周期内的点数，即码元宽度数值输出控件（由采样率Fs/码速率RS后取整得到）。先输入采样点数、采样率、载频以及初始相位等参数，利用正弦波产生器产生载波，规定载波的幅度为1，频率为载频/采样率。因为载波与双极性序列相乘后才能得到2PSK波形。所以，要对上面产生的序列进行极性反转，即当输入为0时，变为-1，输入为1时，变为0。再将输入序列和极性反转后的输入序列相加后即得到双极性序列，将双极性序列与载波相乘后得到2PSK信号输出，对其通过FFT频谱控件进行频谱测量，输出它的频谱图。在2PSK波形图中，1对应的波形与载波极性相同，0对应的波形与载波极性相反。

■ 2.3 2PSK系统解调部分设计

2PSK信号在接收端应先通过带通滤波器滤出噪声，可是本文中假设信道为理想信道，不考虑噪声的影响。所以，直接将2PSK信号与相干载波相乘后送入低通滤波器。低通滤波器的频带设置与双极性码频带设置一致。此处归一化频率为采样率Fs除以码速率RS。考虑到滤波器的过度带，滤波器的最低截止频率取（1+Rs）/Fs[4~5]。最后利用For循环语句作为抽样判决输出解调后的序列。在For循环语句中，首先根据前面求得的一个码元周期内的点数除以2的值与一个码元周期内的点数乘以循环次数的值（i）相加，第一次进入循环时i=0，获得第一个码元中间时刻的抽样值，再让获得的抽样值与0进行比较。因为在双极性序列与载波相乘后得到的2PSK信号中，1的波形与载波极性相同，0的波形与载波极性相反。所以，当2PSK信号在解调时，若大于0为真时，判断输出结果为1，若大于0为假时，即小于0时，判断输出结果为0。在第二次进入循环时，i=1，获得第二个码元中间时刻的抽样值，之后的过程以此类推，便可获得最终的输出序列。

将2PSK调制和解调模块整合起来得到整体框图。点击LabVIEW中自带的整理程序框图按钮整理整体框图，使其更加紧凑，布局更加合理。如图1所示。

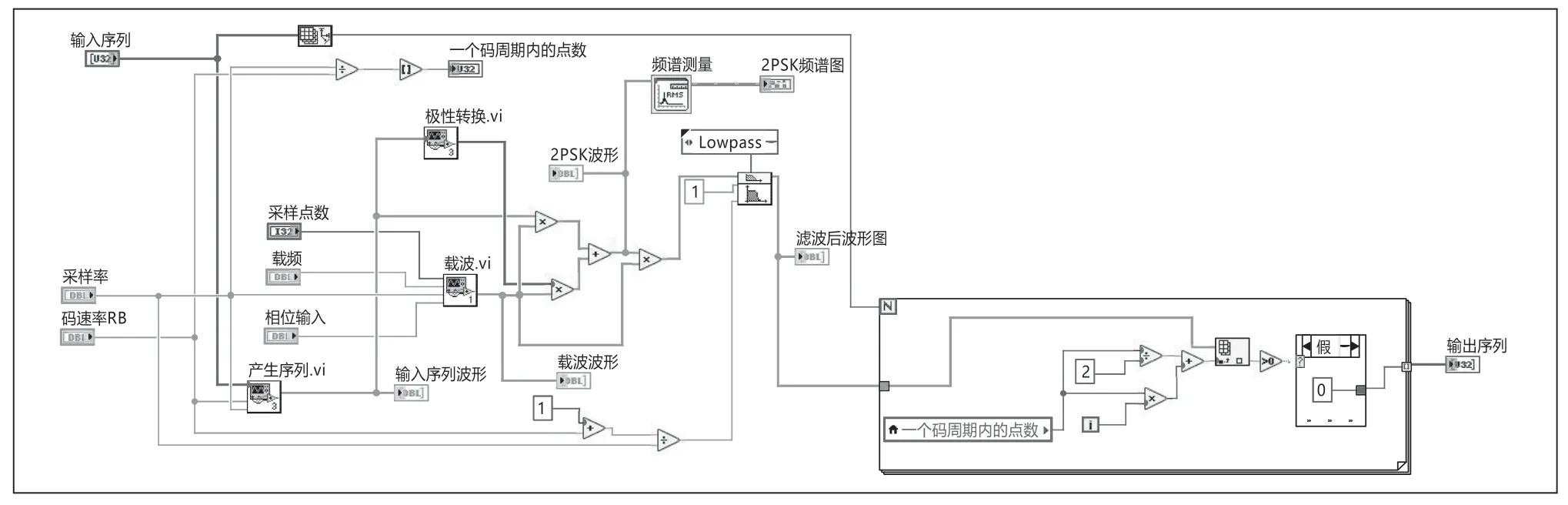
图1 2PSK调制解调系统整体框图

3 仿真结果分析

完成LabVIEW程序的设计后，在2PSK前面板中输入任意序列，本文中输入的序列为“1110111110”，设置载频和码速率为10，采样点数与采样率为1000，相位输入为0，运行仿真。

观察图2和图3，结合2PSK前面板中的2PSK波形，输入序列波形，载波信号波形可以看出，2PSK波形是由双极性基带脉冲信号与相干载波相乘后得到的。在发送“0”和“1”时，2PSK仅相位相差了180°，而它的周期和幅度均无改变。通过分析，我们可以清晰地看出2PSK的调制原理，基带信号只改变了信号的相位，而最终2PSK的波形形状只由相干载波决定。将2PSK前面板中低通滤波后的波形与2PSK波形比较，可以看出2PSK中的高频分量被转换为低频分量输出。

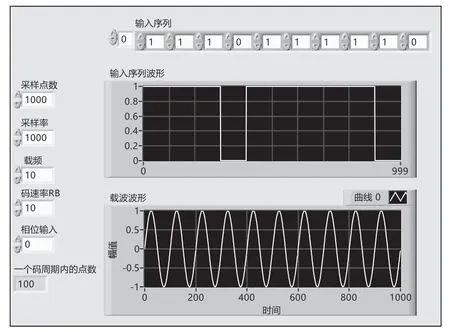
图2 输入序列波形和载波波形

图3 2PSK波形和频谱图

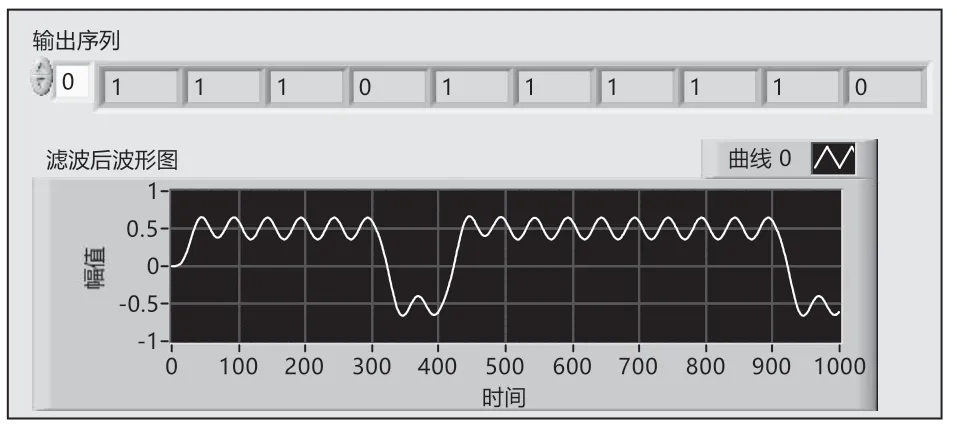
图4 滤波后波形和输出序列

通过比较输入和输出序列可知，解调后的输出序列与输入序列一致，没有出现误码，验证了该仿真系统的正确性，可广泛应用于对2PSK系统的研究。

但是，2PSK在解调的过程中容易发生相位模糊。原因是2PSK信号在解调端与相干载波相乘的过程中，不能保证恢复的相干载波是不是需要的相干载波。由于载波恢复的过程中会存在180°的相位模糊现象，即恢复的相干载波不能确定是否与所需的相干载波同向。假设，“0”用初始相位0来表示，“1”用初始相位Π来表示，恢复的相干载波与所需的相干载波同向，因为“0”对应的波形与相干载波一致，正正得正，所以0相乘出来的结果为正，而1对应的波形与相干载波相反，正负得负，所以1相乘出来的结果为负。再通过抽样判决器，利用阈值电压是否大于零判别，输出还原基带信号。可是，如果恢复的本地载波与所需的相干载波存在180度的相位偏移，则0输出的波形为负，1输出的波形为正，最后使得输出的数字信号全部反了。

该仿真系统中未出现相位模糊是因为在解调2PSK信号时，直接使用了载波信号，而在实际的2PSK系统中使用的应是恢复出的相干载波。

为了解决PSK系统中存在的相位模糊现象，可以采用DPSK技术。PSK技术通过绝对相位表示信号。而DPSK不同于PSK，它是利用载波相对相位的变化来传递信息的。所以，PSK若要正确解调，则必须恢复出正确的相干载波，而DPSK在解调时只要保证相位的相对变化即可，克服了PSK中的相位模糊现象。DPSK有相干解调和差分相干解调两种解调方式。

4 调制技术的发展

随着时代的不断进步，通信技术也在以日新月异的速度同步发展变化着。

在5G通信技术中，常采用16QAM, 64QAM和256QAM等QAM调制方式。QAM技术同时改变了载波的相位和振幅，可以看做是ASK调制技术和PSK调制技术的组合。通过对QAM调制公式的因式分解，可以分解出I，Q两路分量。因此，QAM也可视为对两路正交载波实行幅度调制的调制方式。根据QAM的幅度变化等级，QAM分为4QAM、16QAM、64QAM、256QAM以及1024QAM等，一个调制符号分别可以传送2、4、6、8、10比特的信息，当然对信号质量的要求也逐步提升。16QAM及以上常称为高阶调制。

5 结束语

本文基于LabVIEW软件实现了2PSK系统的调制与解调。通过观察不同阶段的信号结果，更好地理解了2PSK系统的调制解调原理；在比较输出序列和输入序列的过程中，验证了该仿真系统的可行性。在LabVIEW等诸多仿真平台下，我们可以非常方便地修改系统的参数，调整界面，添加新的功能，观察在这些变化下系统的输入输出变化。相比于传统的仪器，这种虚拟仿真方式大大节约了资源，提高了研究效率。