基于alpha 稳定分布的脉冲噪声模拟方法研究*

李召瑞，陈博航，吴晓蓓，郭宝锋

（1.南京理工大学自动化学院，南京 210094；2.陆军工程大学石家庄校区，石家庄 050003）

0 引言

无线通信是指挥控制装备的主要通信方式，无线信号在通信中会受到各种噪声的干扰，从而影响信号传输效果和质量，所以噪声环境的模拟对无线通信系统的性能评估非常重要。如何在实验室产生与无线通信系统实际工作环境匹配的噪声，是通信效能评估领域的热点。

战场范围内，噪声源多样，空间位置多变，传播信道不确定，影响通信背景噪声的因素非常复杂。高斯分布满足中心极限定理，一阶矩、二阶矩有限，易于进行特性分析、参数估计和滤波等处理运算，故传统通信信号处理领域多用高斯分布作为噪声模型。但是大量研究发现，高斯分布并不适合描述可能产生大量数据突变，也就是脉冲性很强的噪声条件，在一些场景中采用高斯分布对噪声建模会出现很大的误差，导致噪声模型失配，造成信号处理算法性能下降，甚至失效。在中国多地、北极、澳大利亚等地的背景噪声测量结果表明，整个噪声体系中，由于大量电气化设施、用频设备的使用，人为的窄带信号干扰和脉冲噪声已经占据主导地位。在战场电磁环境中，特别是短波超短波频段，包含各种随机通信产生的数字脉冲、战场雷达杂波信号、电子对抗装备干扰信号和工业辐射干扰信号等成分，恰恰是随机脉冲性很强的噪声，这样的噪声一般被归属为非高斯噪声类别。非高斯噪声指的是不服从高斯分布的噪声，其特征表现为频繁出现大幅度尖峰类异常值，对于这种呈现短时随机冲击特性的噪声，一般统称为脉冲噪声。非高斯脉冲噪声在很多自然和人为噪声环境中广泛存在，如大气噪声、水声噪声、电话线路噪声、无线通信中的干扰、雷达杂波等。

既定噪声下信号处理的一般研究思路是：建立噪声的数学模型，并进行模型参数估计，从而获得噪声特性描述，根据噪声特性开发信号处理算法。当前描述噪声的模型主要包括两类，即统计物理模型和数学经验模型。统计物理模型从真实物理信号出发，需要通过综合考虑噪声源在空间中分布位置、噪声源发射信号的波形特征、噪声信号在物理信道中的传播特性等因素生成，由于战场环境下噪声源类型多、信号发射随机性强、地形地貌复杂、传播特性多变，建立物理模型复杂度太高，所以这种方法用的比较少。数学经验模型则不考虑噪声产生、传输、处理的物理机理，直接选择适当的数学模型，依据现地观测噪声对模型进行参数估计，拟合其实际物理特性。目前，常用的非高斯脉冲噪声的数学经验模型主要有4 种：高斯混合、t 分布、广义高斯和α 稳定分布。其中，α 稳定分布是一种典型的厚尾分布，在上述脉冲噪声的数学经验模型中，α 稳定分布模型应用最广泛。

α 稳定分布的重要特点是概率分布上的稳定性和概率密度函数（probability density function，PDF）具有厚重拖尾，其分布特性可以匹配物理、化学、生物等学科的多种现象和变化，作为数学模型得到了广泛应用。α 稳定分布最早由Levy 在1925 年提出，丹麦物理学家Holtsmark 将其用于描述星际间引力场的随机波动，并且还估计出对应的特征参数α 为1.5。1993 年，Shao 和Nikias 将分数阶微积分理论与α 稳定分布结合起来，推进了基于分数低阶统计量的信号处理理论的发展。在噪声拟合方面，α 稳定分布不仅被成功用于大气噪声、电话电流噪声的建模，在其他脉冲噪声场景中也获得了广泛应用，例如：水下声学噪声、雷达杂波、电力线通信信道脉冲噪声和无线网络中的网络干扰等。利用α 稳定分布模型进行噪声建模的优势在于：模型数学定义完善，特征函数可解析表达、形式简洁，便于进行理论分析，与统计物理模型具有紧密的联系。

本文以α 稳定分布作为数学经验模型，介绍其性质，通过分析其概率分布，确定其与脉冲噪声的匹配性，研究了α 稳定分布参数估计方法和随机数生成方法，以及参数估计精度验证方法。依据雷达、通信装备固定工作场景的采集数据，对拟合的α 稳定分布参数进行估计，确定了参数范围，为既定噪声条件下通信系统性能度量奠定基础，形成了真实性更强的环境噪声模拟方法与手段。

1 α 稳定分布模型

1.1 定义

首先介绍稳定分布定义：假设X、X是随机变量X 的独立样本，若对于任何正数A、B，都存在正数C 和实数D 满足

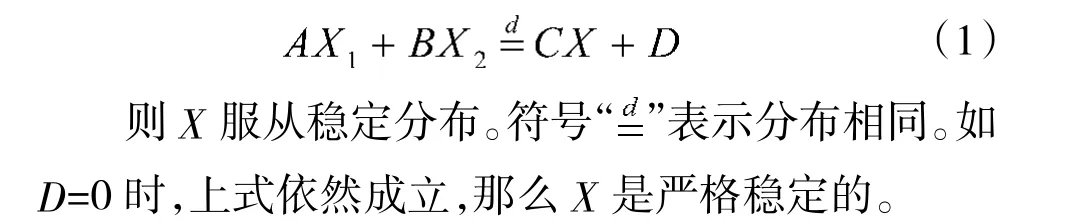
α 稳定分布的定义为：针对上述稳定分布的随机变量X，如果存在一个数α∈（0，2］，使满足式（1）的A、B、C 满足

那么称X 符合α 稳定分布。α 稳定分布通常没有封闭的概率密度函数解析式，但是存在统一的特征函数表达式：

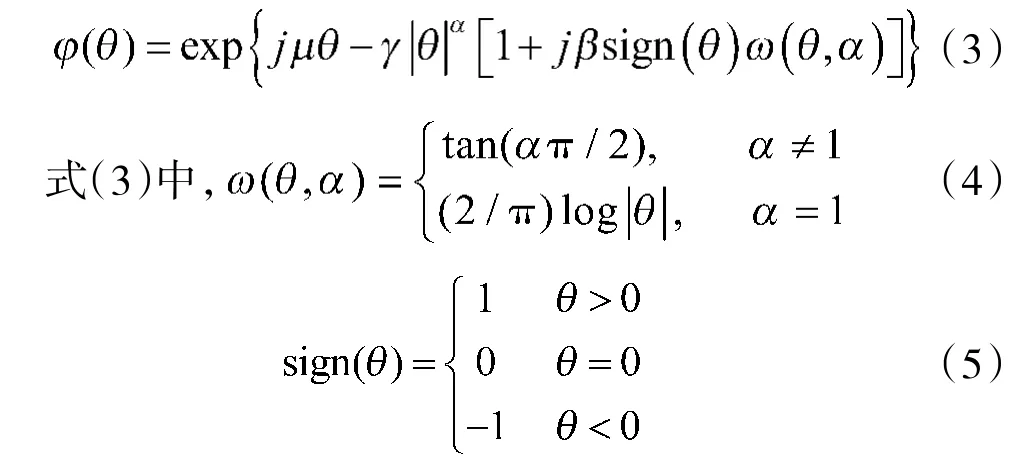
其中，α 为特征指数，取值范围是0＜α≤2，特征指数α 决定了稳定分布概率密度函数的脉冲程度，α 值越小，脉冲性越强，也就是大幅值突变脉冲出现的概率越高，在概率密度分布上表现为拖尾越厚；α 值越接近2，脉冲性越弱，越接近高斯分布，当α=2 时，α 稳定分布退化为高斯分布。所以说，α 稳定分布是高斯分布的广义化形式，高斯分布是α 稳定分布的一个特例。

β 为偏斜指数，取值范围是-1≤β≤1，该参数决定了α 稳定分布概率密度函数的偏斜程度。当β=0 时，α 稳定分布是对称α 稳定分布（symmetric α stable，SαS），β＞0 和β＜0 时，分别表示分布是左偏斜分布和右偏斜分布，数值大小表征了偏斜程度。

γ 为分散系数，取值范围是0＜γ＜+∞，该参数用以描述随机变量偏离均值或者中值的程度，其含义和高斯分布中的方差类似。高斯分布情况下，它的值等于方差的一半，即2γ=σ。

μ 为位置参数，用于描述α 稳定分布概率密度函数的绝对位置。对于SαS 分布，当1＜α≤2 时，μ与α 稳定分布的均值相等；当0＜α＜1 时，μ 与α 稳定分布的中值相等。

当μ=0，γ=1 时，α 稳定分布称为标准α 稳定分布；当α=2，β=0，γ=1/2σ时，分布为高斯分布；当α=1，β=0 时，分布为柯西分布。

1.2 α 稳定分布概率密度函数

相对于时域波形，概率密度函数能够更加直观地展示数据的分布特性，α 稳定分布的概率密度只有特殊情况下才能有解析的表达式，很多情况下只能通过数值方法来求取。Fourier 逆变换法和渐进级数展开法可以获取既定条件下分布的概率密度。

1.2.1 Fourier 逆变换法

当μ=0，γ=1 时，α 稳定分布为标准α 稳定分布，通过对特征函数进行Fourier 逆变换，可得到其概率密度表达式

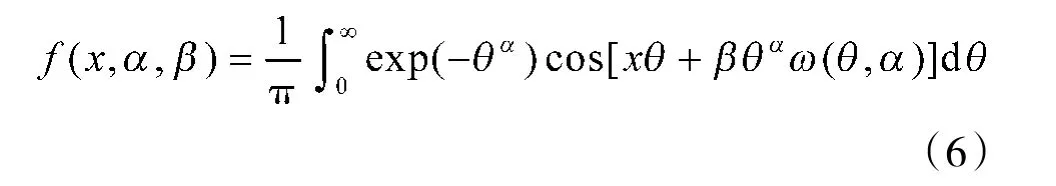
μ、γ 不满足标准α 稳定分布条件时，只有高斯分布、柯西分布、Levy 分布几种情况存在封闭的表达式。

1.2.2 渐进级数展开法

标准α 稳定分布的概率密度函数的幂级数展开式可以获得，并且级数为绝对收敛的。函数表达式为

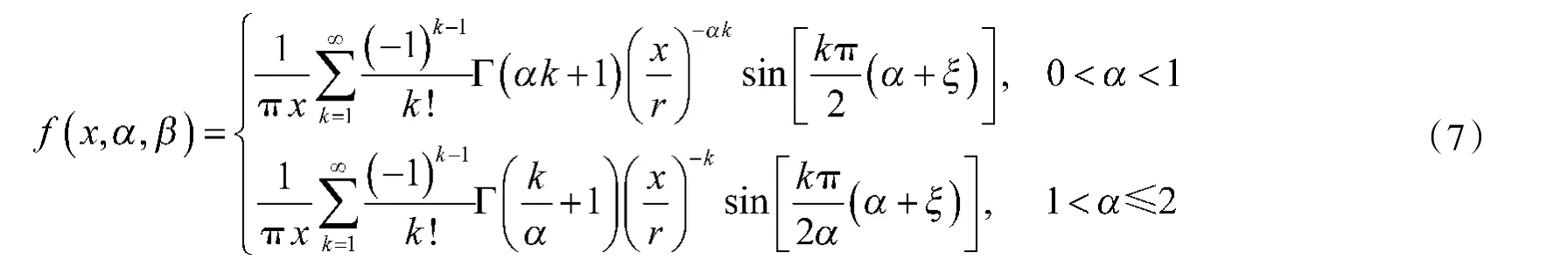
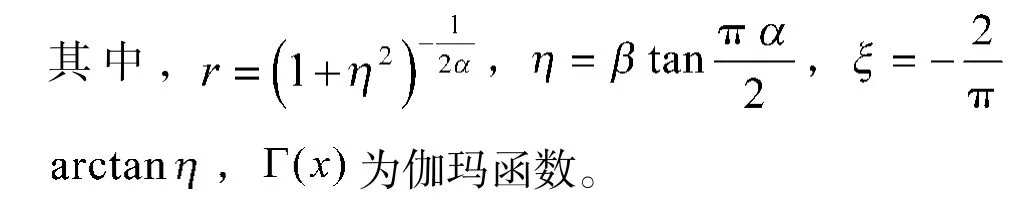
此处给出的α 稳定分布概率密度函数限制条件较多，多为固定条件下的分布，但是在研究α 稳定分布下的信号处理问题时，这些特例都非常具有代表性。除上述集中特例外，α 稳定分布只可以用数值方法得到概率密度曲线。图1 为不同α 取值下的对称α 稳定分布的概率密度曲线，当α 取值趋近于2 时，其输出信号被局限在一定幅度，α 取值越小，概率密度曲线出现越来越厚的拖尾，表示幅度异常值越来越多，且幅值越来越大。

图1 不同α 值下概率密度曲线

综上所述，α 稳定分布模型存在稳定的概率分布，且便于模拟异常值多、异常幅值高的脉冲性噪声，所以本文选择α 稳定分布模型对战场脉冲型噪声环境进行模拟。

2 α 稳定分布随机数的生成

α 稳定分布随机数的生成是一种噪声模拟实现方法，本文研究的一个主要内容就是α 稳定分布随机数生成方法。基于Janicki-Weron（JW）算法可得到稳定分布随机数。当α≠1 时，应用下式

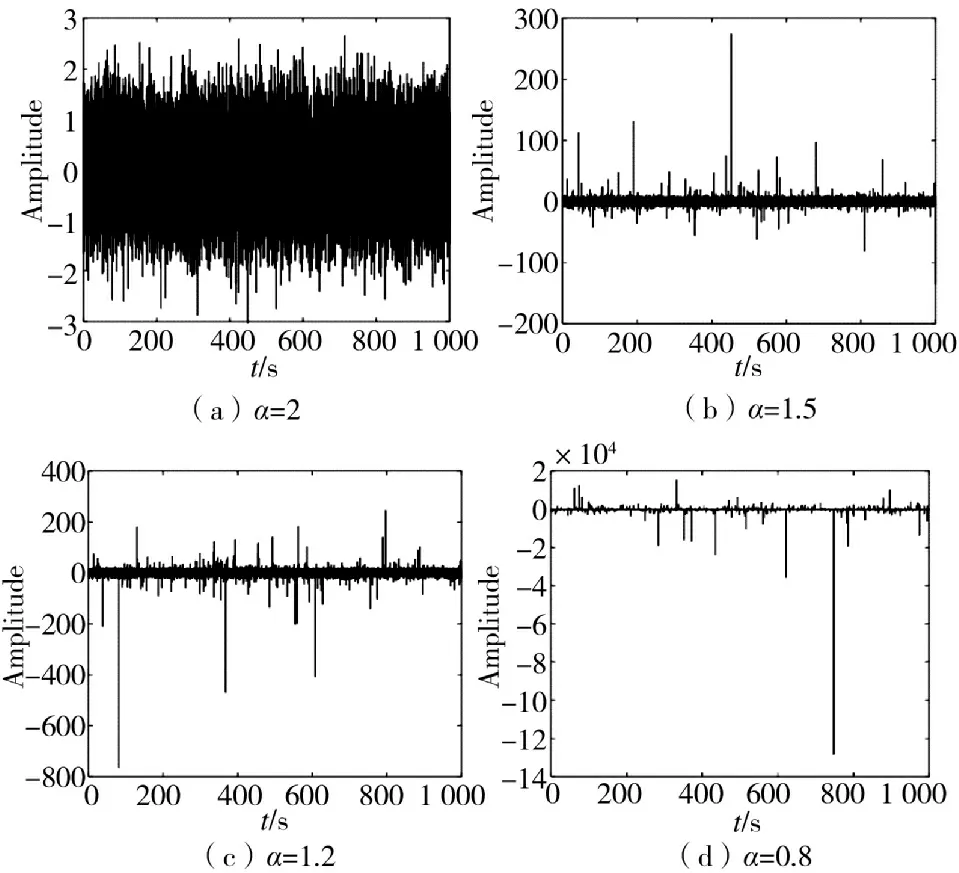
图2 β=0，γ=0.5，μ=0 时，不同α 值时生成的α 稳定分布随机数时域图

3 α 稳定分布参数估计

在进行通信信号处理的相关算法研究时，可以用α 稳定分布模型产生所需的噪声数据，但是α 稳定分布的参数选取不同，产生的噪声数据差异非常大。为提高模拟噪声的针对性、真实性，需要用α 稳定分布模型去匹配真实战场环境的噪声分布，这涉及到了噪声模型参数估计的问题。解决问题的思路是，针对特定场景采集到的噪声信号，首先进行非高斯性判定，确定采集的环境噪声是否为非高斯脉冲性噪声；然后依据实采数据进行参数估计，确定参数的取值范围，后期实验即可依据估计结果进行噪声模拟，以此增强噪声的真实性。噪声对称与否，参数估计的算法不同，所以参数估计前还需要通过正、负数值统计进行对称性判定。本文主要以对称α 稳定分布为例开展研究，即β=0；μ 是噪声概率密度函数的位置参数，仅表征左右平移特性，对噪声性质没有影响，所以下文主要研究α、γ 的估计方法。

3.1 分数阶矩法参数估计

随机变量统计矩包含丰富的信号特征，高斯分布的统计矩可以从零阶一直计算到无穷阶，一阶矩、二阶矩可用来分析服从高斯分布的信号。但α稳定分布由于存在大量脉冲值，不存在有限的方差，高阶统计矩更是不存在，分数低阶矩理论（fractional low order moment，FLOM）为α 稳定分布的参数估计提供了有效的分析方法，本文主要采用分数阶矩法实现参数估计。针对脉冲型噪声的参数估计，本文先通过时域统计法，选取对称型噪声，基于对称α 稳定分布模型实现噪声的参数估计。

3.1.1 对称α 稳定分布分数低阶矩定义

式（9）中，γ 是分散系数，满足γ=σ，C（p，α）是参数p和α 的函数，与X 无关。1995 年，Ma 和Nikias 提出了分数负阶矩的定义，可表示为

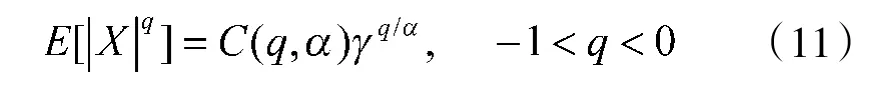
3.1.2 分数阶矩法参数估计

变换可得到参数α 的估计式

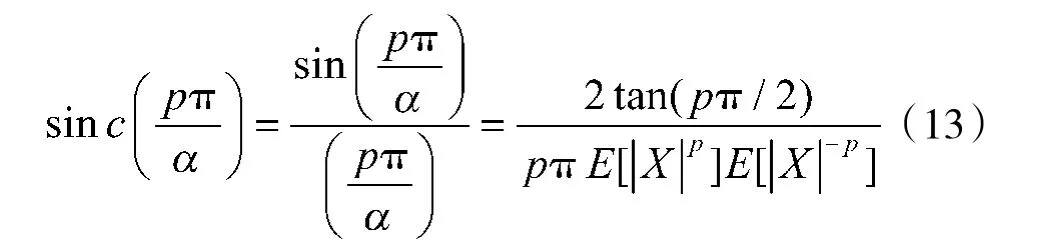
针对已知样本数据进行参数估计时，有

3.2 参数估计精度验证

针对参数估计的可信度问题，以已知的α 稳定分布随机数作为对象，利用分数阶矩法进行参数估计，分析参数p、样本点数目、α 取值不同对参数估计的影响，比较参数估计值与理论值的差异，达到评估参数估计精度的目标。本节以对称α 稳定分布模型α 值的估计为例进行分析，斜α 稳定分布的评估方法与此类同。

3.2.1 参数p 取值对α 估计值的影响分析

p 取值不同，会影响α 值的估计精度，在p 取不同值的条件下对α 进行估计，分析得到在不同条件下p 的最优取值范围。应用JW 方法，生成α=0.8，β=0，γ=1，μ=0 的稳定分布随机数，样本点取10 000个，分别在p 取不同值的条件下进行参数估计，可多次估计取均值，结果如图3 所示。

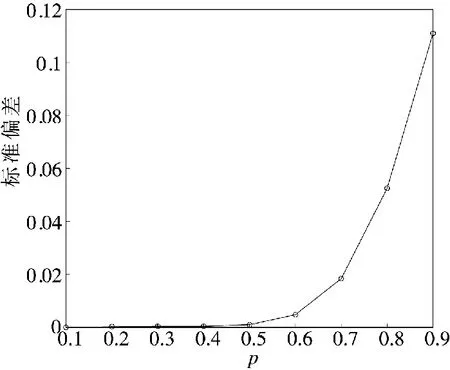
图3 p 取不同值对α 值估计的偏差

由图3 可以看到，p 值越小，估计值精度越高，当取值大于0.4 后，估计值偏差明显增大，与理论分析结果相符，所以，p 的最佳取值范围为0～min（α/2，1），并尽量取较小值。

3.2.2 样本点数目对参数估计值的影响分析

同样应用JW 方法，生成α=0.8，β=0，γ=1，μ=0的稳定分布随机数，改变样本点数目进行参数估计，结果如图4 所示。

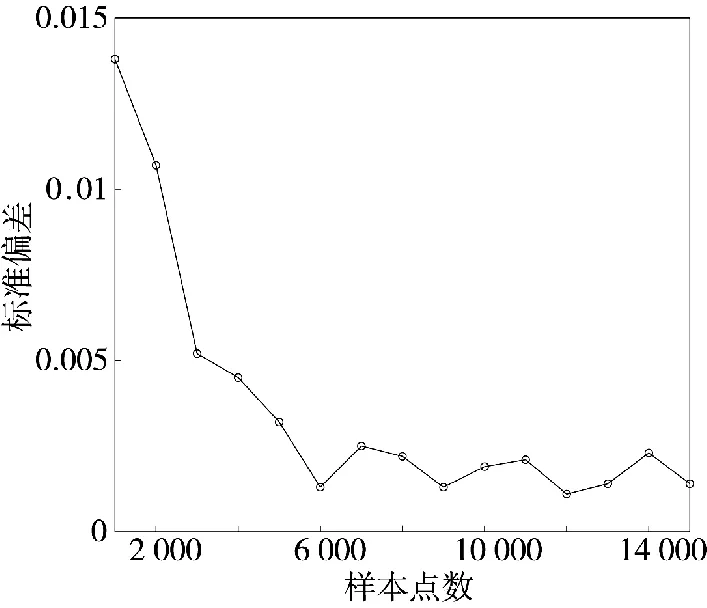
图4 不同样本点数对α 值估计的偏差

由图4 可以看到，样本点越多，估计精度也越高，符合一般规律。但是随着样本点增多，计算量也会加大，根据统计结果，取样本点为5 000 以上，此时参数估计误差较小。

3.2.3 α 取值对参数估计值的影响分析

α 取不同的值，对其本身的估计结果也会产生影响。应用JW 方法，生成β=0，γ=1，μ=0 的稳定分布随机数，进行参数估计，可多次估计取均值，结果如图5 所示。

图5 不同α 取值下α 值估计偏差分析

由图5 可知，随着α 增大，参数估计的误差也越大。得到α 的估计值后，根据式（16）即可计算出γ 的估计值，篇幅所限，本文不再详细阐述。分析可得：p取值越小，γ 的估计值越准确，样本点越多，估计精度也越高，γ 值越大，估计值与实际值的偏差越大。

3.3 基于实采数据的模型参数估计

3.3.1 环境构建

本次采集环境使用的装备包括3 辆指挥车、1部中低空目标指示雷达、1 部战场活动目标侦察雷达，以及短波超短波电台若干。应用RFBOX-6G 型射频信号采集记录回放仪作为采集设备，针对超短波波段，采样带宽设为100 MHz～500 MHz，采样率为240 MSPS～1 000 MSPS，进行了长达1 h 的数据采集。采集场景如图6 所示。

图6 战场环境数据采集场景图

3.3.2 采集结果分析

针对装备关机、电台开机、雷达开机、电台发射、雷达发射等装备不同工作模式采集环境噪声数据，进行记录并存储。数据采集结果示例如下页图7 所示。

图7 数据采集结果示例

针对采集的数据进行参数估计，为保证随机性，主要采用从30 min 的采集数据中序列截取的方式，综合考虑数据特征抓取与计算量的平衡，令截取数据点数N=100 000。分别进行50 次和500 次估计，结果如图8、图9 所示。

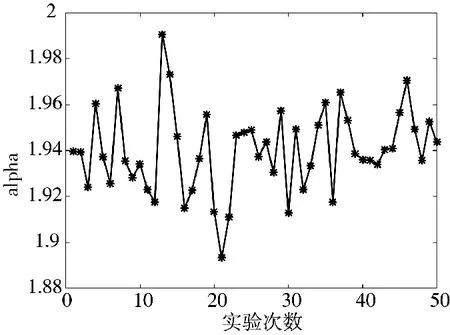
图8 50 次实验参数α 估计结果

图9 500 次实验参数α 估计结果

实验结果可知，由于用频设备的信号发射是在以min 为尺度情况下实施的，大部分时间是没有发射信号的，所以很多情况下，α 的取值多在接近2 的较大值范围内，得到的α 值在1.88～1.98 之间，如图8 所示。图9 选取有辐射信号情况下进行参数估计，可明显看到脉冲性特征，但是，即使在近距离大功率的条件下，参数α 估计值也很难低于1.5，所以后面针对α 稳定分布噪声下通信系统性能研究，以主要针对α＞1.5 的情况开展为宜。γ 值的估计与采集点位置、辐射源类型等密切相关，本文估计值多在0.3～0.8 之间，能够体现出与距离、辐射功率等指标的相关性。

4 结论

本文针对战场环境噪声特点，选用α 稳定分布作为噪声模型，研究了α 稳定分布随机数产生方法和参数估计方法，针对特定装备工作场景采集的噪声数据进行参数估计，并分析了参数估计精度，量化得到了模型参数取值特征和范围，根据参数范围可产生对应工作场景的噪声数据。本文提出的噪声模拟方法和形成的量化结论，对提高电磁环境噪声模拟的针对性和真实性具有重要意义。