狙击弹侵彻玻璃的弹道特性研究

2022-09-14康斌会张国伟龚建华荣洪霞高树华

火力与指挥控制 2022年7期

康斌会，张国伟，*，龚建华，荣洪霞，高树华

（1.中北大学机电工程学院，太原 030051；2.重庆嘉陵特种装备有限公司弹药技术中心，重庆 400032；3.武警特种警察学院特种作战系，北京 102211）

0 引言

随着社会的进步，科技的发展，人们对更高生活水平的追求也越来越高，从室内装修就很容易体现，为了提升装修格调，美观大气、易清洁，且能让视野开阔的玻璃就成为人们喜爱的建筑材料。但是现在也出现了一些新问题，如：在城市发生挟持人质事件时，歹徒常常挟持人质躲藏在室内或者车内，狙击手隔着玻璃射击恐怖分子是否可以保证人质或周边群众安全，怎样才能准确击毙歹徒而不伤人质成为一个重要问题。国外曾有学者在研究了0.38 in 特种弹穿过钢化玻璃的弹道偏转和0.22 in子弹穿过窗户玻璃的偏差，但是并未明确子弹以不同入射角穿透玻璃后的偏转大小。本文通过ANSYS/LS-DYNA 有限元软件模拟分析，探究7.62 mm狙击弹以不同入射角穿透单层钢化玻璃对弹道的偏转的影响，为狙击手击毙歹徒或恐怖分子提供参考。

1 仿真方案

根据GB17840-1999 防弹玻璃标准中介绍得知，79 式7.62 mm 狙击步枪初速大约为830 m/s，子弹速度取800 m/s；根据苑大威等提到步枪弹的攻角为0°～2°，随着子弹飞行距离增大，攻角也逐渐变大。因此，本文仅考虑子弹在着靶前稳定飞行，故攻角取±2°。假设速度方向在弹轴右侧时，攻角记为+2°，速度方向在弹轴左侧时，攻角记为-2°；狙击弹侵彻钢化玻璃时，入射角（子弹弹体轴线与玻璃靶板外法线方向的夹角）为α，本文中入射角α 在0°～60°之间，间隔为5°，分析不同入射角对狙击弹穿透玻璃的弹道偏转影响，共计有26 组仿真。

设狙击弹穿透钢化玻璃后飞行的距离AB 为L，利用软件LS-DYNA 模拟出来的子弹穿透玻璃飞行一定距离L 时，水平位移为Xtrue，垂直位移为Ztrue。理想状态下，狙击射击目标前透过钢化玻璃看到目标水平方向的距离BC 为Xsee，垂直方向的距离CD 为Zsee，如图1 所示。由于入射角度的不同，狙击弹真实穿过玻璃的厚度也有所差异，根据计算得出狙击弹真实穿过玻璃的厚度δtrue=δ/cosα。射击者利用基本瞄准原理得出的目标水平方向距离为Xsee=δtrue+L，偏转距离ΔX=Xsee-Xtrue。

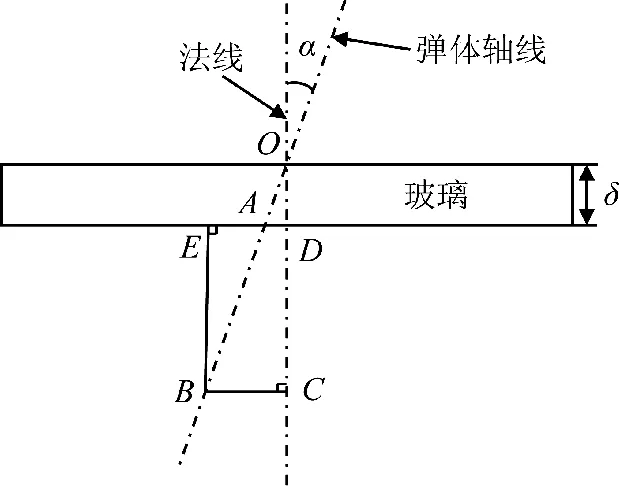
图1 理想状态下子弹轨迹示意图

2 数值模拟

2.1 材料模型

本文中子弹头由弹芯、被甲构成。JOHNSON_COOK 材料模型适合描述材料在大变形、高应变率和高温条件下的本构关系，在弹道侵彻冲击、金属爆炸成型等数值计算中应用较广。因此，子弹的弹芯和被甲均采用该材料模型描述。其本构关系的表达式为：

式中，D、D、D、D、D分别为第1～第5 断裂参量。另外，使用JOHNSON_COOK 材料模型需要结合GRUNEISEN 状态方程来描述材料变形情况。*EOS_GRUNEISEN 状态方程定义压缩状态下材料的压力为：

钢化玻璃属于脆性材料，密度2.53×103 kg/m，最大抗拉强度150 Mpa。由于子弹在侵彻过程中，玻璃靶板发生大变形，因而采用改进模型MAT_JOHNSON_HOLMQUIST_CERAMICS，也称为JH2 模型，这样也有利于侵彻过程中玻璃裂纹的呈现。该模型主要有3 部分构成：第1 部分用于描述钢化玻璃的强度，表达式如式（6）、式（7）所示。

表1 子弹JOHNSON_COOK 材料模型参数（单位：g-cm-μs）

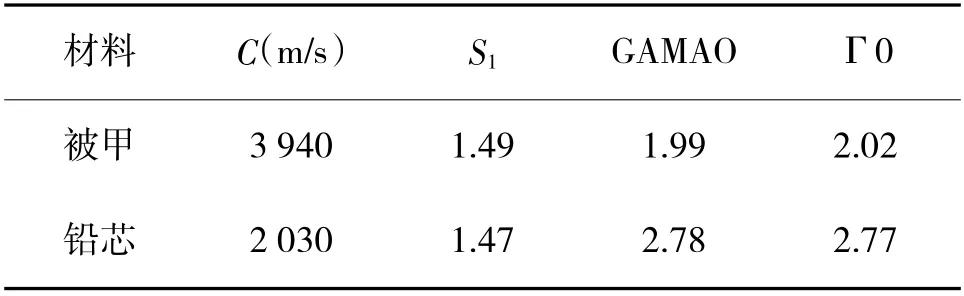
表2 材料GRUNEISEN 状态方程参数

第2 部分用于描述侵彻过程中玻璃的损伤情况，表达式如式（8）、式（9）所示。

第3 部分用于描述玻璃的应力-应变曲线，表达式如式（10）所示。

式（6）～式（10）中，A、B、C、M、N 为材料常数；P*=P/PHEL，归一化压力；T*=T/PHEL，归一化的最大拉伸静水压力，T 为玻璃的最大抗拉强度；Δε是塑性应变；D、D是塑性应变断裂参数，可以提高与失效不相邻表面材料的强度；D 为损伤因子，0≤D≤1；K、K、K为常数，其中，K为体积模量，与材料有关；μ 是关于密度和体积的函数。钢化玻璃的材料模型参数如表3 所示。

表3 钢化玻璃材料模型参数

2.2 仿真模型及算法

2.2.1 仿真模型

根据枪弹手册中对7.62 mm 口径子弹的介绍，利用TrueGrid 软件建立子弹的有限元模型，共有15 336 个SOLID 单元，如图2 所示。由于子弹与靶板的尺寸相差较大，故玻璃靶板建为400 mm×400 mm，厚度δ 为5 mm，四周添加非反射边界，子弹与玻璃接触附近划分较密的网格，网格尺寸与弹头单元尺寸接近为0.2 cm，在与之接触区域较远的位置划分较粗的网格，单元尺寸为0.4 cm，玻璃靶板共有91 200 个SOLID 单元。如图3 所示。

图2 子弹有限元模型

图3 钢化玻璃有限元模型

2.2.2 仿真算法

采用LS-DYNA 软件进行数值模拟，被甲、弹芯、钢化玻璃均采用拉格朗日算法，空气域采用ALE 算法，弹芯与被甲之间采用面面自动接触，被甲与钢化玻璃之间采用自动面面侵蚀接触算法。根据文献［13］得知，金属与非金属之间的静摩擦系数和滑动摩擦系数分别为0.5、0.08。由于单点积分的lagrange 算法在单元大变形时会产生严重的沙漏变形，因此，采用5 号刚性的沙漏控制算法，设置沙漏系数为0.05。这样可以较好地抑制沙漏对数值结果可靠性的影响。

3 数值模拟结果与分析

文中狙击弹穿透玻璃后飞行0 m、0.1 m、0.2 m、0.3 m、0.4 m，分别用工况1～工况5 来表示。下文分别对子弹质心的位移、弹体偏转角、质心偏转距离进行分析，进而得出不同入射角下狙击弹偏转距离的大小，为狙击手射击提供参考。

3.1 飞行姿态分析

图4、图5 为狙击弹穿透钢化玻璃飞行0.4 m时，不同入射角情况下，子弹水平位移、垂直位移随入射角的变化曲线。由于玻璃的影响，狙击手射击时还需考虑目标与着靶点法线的水平距离，在图4中可以看出，随着入射角的增加，水平位移也在逐渐增加。一般情况，人站立在玻璃窗户前面，头颅距离玻璃的垂直距离为20 cm 左右，如若出现挟持人质的情况，这个距离可能会更大。所以，分析垂直距离20 cm～43.3 cm 时的入射角。由图5 可以看出，入射角在0°～60°之间均满足条件。

图4 工况4 不同入射角时的水平位移

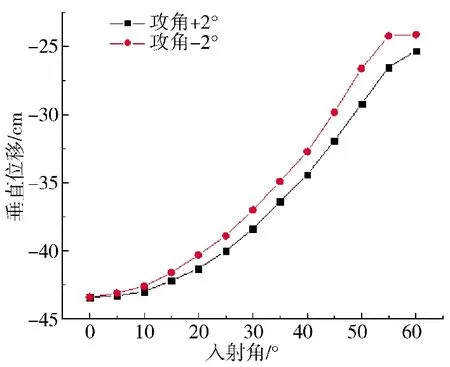
图5 工况5 不同入射角时的垂直位移

为了研究狙击弹穿透玻璃后子弹偏转的影响，须分析入射角对弹体偏转角（弹体轴线与玻璃靶板法线的夹角）的影响。图6 为弹体偏转角曲线，经分析可知，攻角为+2°时，狙击弹穿透玻璃后飞行距离越短，弹体偏转角越小；攻角为-2°时，狙击弹穿透玻璃后，飞行距离对弹体偏转角的影响较小。随着入射角的增大，穿透玻璃后，弹体偏转角就越大，弹体也就越趋于水平，越容易发生跳弹行为。由于人的头骨比较硬，一般情况入射角大于65°，子弹会发生跳弹。因此，得出入射角在0°～45°之间，子弹击中目标不会发生跳弹。攻角为-2°时，入射角在25°～35°之间，弹体偏转角几乎不变，子弹穿靶后飞行相对较稳定，也不会发生跳弹。

图6 弹体偏转角

通过分析不同组合下弹丸质心、弹轴变化情况，可以得出随着入射角的增加，穿透玻璃后弹体偏转角也增大；综合考虑得出入射角在0°～45°之间时，子弹穿透玻璃后飞行较稳定，且不易发生跳弹。

3.2 弹体偏转距离分析

由图7（a）可以看出，狙击弹穿透玻璃后，子弹质心偏转方向均由正攻角向负攻角方向转变，狙击弹穿透玻璃后的偏转距离ΔX 随着入射角角度的增加而增加，且偏转距离呈线性递增。当攻角+2°时，入射角在0～25°之间时，随着狙击弹穿透玻璃后飞行距离的增加，子弹质心偏转距离负攻角方向减小，正攻角方向增加。入射角在30°～60°之间时，随着狙击弹穿透玻璃后飞行距离的增加，子弹质心偏转距离也随之减小，且呈递减趋势。

图7 偏转距离曲线

由图7（b）可以看出，狙击弹穿透玻璃后，子弹质心偏转方向均向负攻角方向偏转，且偏转距离接近线性递增。当攻角-2°时，随着狙击弹穿透玻璃后飞行距离的增加，子弹质心偏转距离也随之增大，且呈递增趋势。入射角角度越大，偏转的距离就越大，当入射角为45°时，子弹穿透玻璃后飞行0.4 m时的偏转距离为3.36 cm；入射角为60°时，子弹的偏转距离可为4.33 cm。因此，在挟持事件中，必须采取隔着玻璃射击目标时，应尽可能在小入射角下进行射击，其中，入射角度为0°时，偏转距离最小。