基于机器学习的卷烟制丝工艺物料衡算模型

张艮水，关爱章，兰志超，袁海霞，林盈，杨明，曾伟中，郑茜

（湖北中烟工业有限责任公司襄阳卷烟厂，湖北 襄阳 441000）

0 引言

在人工智能、机器学习等新兴技术日趋成熟的背景下，制丝生产过程的智能化应用逐渐成为行业的主要研究方向。目前，制丝过程消耗计量问题一直制约着工厂高级排产、过程仿真、批次物料追踪和智能数据分析等智能化应用。基于此，本文对制丝全流程物料衡算关键技术进行系统性研究，以数据驱动和知识驱动为基础构建制丝全流程物料衡算模型，从而对损耗过多、产出不稳定等现象进行预警。通过数据分析及预测模型研究，对制丝生产过程的物料进行精准计量，可进一步挖掘质量数据价值，提升烟厂智能制造水平，为未来智能化、数字化建设提供数据支撑。

在机器学习方面，相关研究涉及领域十分广泛。吴勇，等构建了面向审计全生命周期的机器学习应用模型；宋祥，等采用决策树、贝叶斯分类器、神经网络、逻辑回归等六种机器学习算法对个人年收入进行了预测；喻佳，等通过逻辑回归、决策树、贝叶斯算法、随机森林等五机器学习算法对教育大数据进行了分析；黄家宸，等分析了机器学习技术在油气领域的主要应用场景以及在产量预测中存在的问题。

在物料衡算方面，大部分研究主要集中在化工生产领域。史忠录，等对氯化钾工艺的“冷结晶—正浮选—洗涤法”生产过程进行了物料衡算；张瑜通过具实际案例对精细化工项目工艺的物料衡算进行了具体分析；陈旭辉，等通过实际数据对一步法腈纶纺丝工段进行了物料衡算以改进浴液系统；姜京哲，等对五氧化二钒的生产过程进行物料衡算和水平衡计算，以此为环保治理提供建议。

通过文献检索可知，关于机器学习和物料衡算的研究较多，但尚未有文献将机器学习技术应用于烟草行业的制丝工艺物料衡算。本研究以数据驱动和知识驱动为主要技术路线，采用机器学习技术建立全流程、自学习的制丝物料消耗衡算模型，以填补相关理论在这一领域的空白。

1 卷烟制丝工艺流程分析

1.1 主要流程

烟草生产的工艺流程主要分为两个部分：制丝和卷接包装。制丝工艺主要对烟叶、烟梗等原料通过回潮、切丝、干燥、掺配混合、加香等一系列加工工序处理，得到符合卷制包装技术要求的烟丝。烟丝经过输送设备送至卷制包装。具体制丝工艺流程如图1所示。整个过程十分复杂，具有非连续、流程长、参数多、要求高等特点。制丝生产所得烟丝的质量直接影响着卷烟产品质量的稳定，为此，通过数学建模、数据分析，对制丝生产过程的物料进行精准计量，挖掘质量数据价值，提升制丝加工精度。

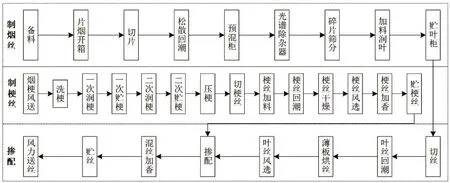
图1 卷烟制丝工艺流程

1.2 影响因素分析

制丝工艺受诸多因素影响，主要包括烟丝的理化性质、环境因素、物料因素、设备因素、人为因素等方面，任一因素变化都将对烟丝品质产生影响。物料衡算技术是制丝物料损耗、批次稳定性、排产仿真和工艺质量控制的重要基础，也成为工厂智能化数字化建设重要研究领域，因此，十分有必要对制丝工艺进行物料衡算，并分析这些因素变动对烟丝质量的影响，从而实现制丝生产的精益管控。物料衡算的影响因素主要有：

（1）水分含量：制丝工艺多个环节涉及物料的回潮和干燥，并且水分含量对烟丝的颜色、光泽、味道等指标起着关键作用，同时影响着烟丝产出比。对于制丝工艺流程的松散回潮、洗梗润梗、梗丝干燥、加香喂料等环节，在工序出入口配置水分仪和电子秤，以便对物料进行自动称重，并实时监控物料的水分含量，严格控制水分，以实现对制丝工艺的管控。

（2）机器设备：主要依靠水分仪和电子秤进行计量，以实现对物料流量的精准控制。对于物料回潮、干燥、掺配混合、加香加料等关键工序，保持物料水分及重量等数据计量的准确性，对后续流程中原料和辅料的掺兑配比等工作具有重要的参考意义。

（3）工艺技术：制丝工艺的精准控制，依赖先进的工艺技术，根据不同牌号的生产需求设计标准化的生产加工路线，保障生产过程的稳定性和柔性化。

当前，烟草行业普遍存在物料计量体系不完善、卷烟生产消耗管控人工干预多、耗时费力且工作效率低等问题。基于此，本文采用线性回归、多项式回归及BP神经网络多种机器学习方法，根据历史数据，结合专家经验进行数据建模，将物料衡算模型结合数据可视化、数据预警等技术以形成一套科学完整的制丝全流程物料计量体系，辅助未来数字化工厂精益化生产和创新应用，为生产决策智能化奠定基础，提升工厂智能分析和决策水平。

2 基于机器学习的物料衡算模型建立

2.1 模型构建思路

2.1.1 总体框架。机器学习能够对大量历史数据进行分析和处理，挖掘数据隐含规律，通过不断改进经验或模型达到自适应学习的目的，十分适用于制丝生产线的物料衡算。机器学习包括线性回归、多项式回归、梯度下降、聚类分析、神经网络等多种算法。其中，线性回归和多项式回归是用于预测的经典算法，分别利用线性和非线性模型分析自变量和因变量的数学关系，根据回归方程预测因变量的变化趋势。BP神经网络是近年来使用最广泛的机器学习算法，通过模拟人类神经元的结构，对输入和输出的大量数据进行采集和存储，在非线性系统中表现较好。本文选择线性回归、多项式回归及BP神经网络算法作为候选模型，利用线性和非线性原理，对每个工段所涉及自变量和因变量之间的关系进行拟合。最后通过对比分析，选取误差最小的物料衡算模型。总体建模框架如图2所示，主要包括以下两个阶段。

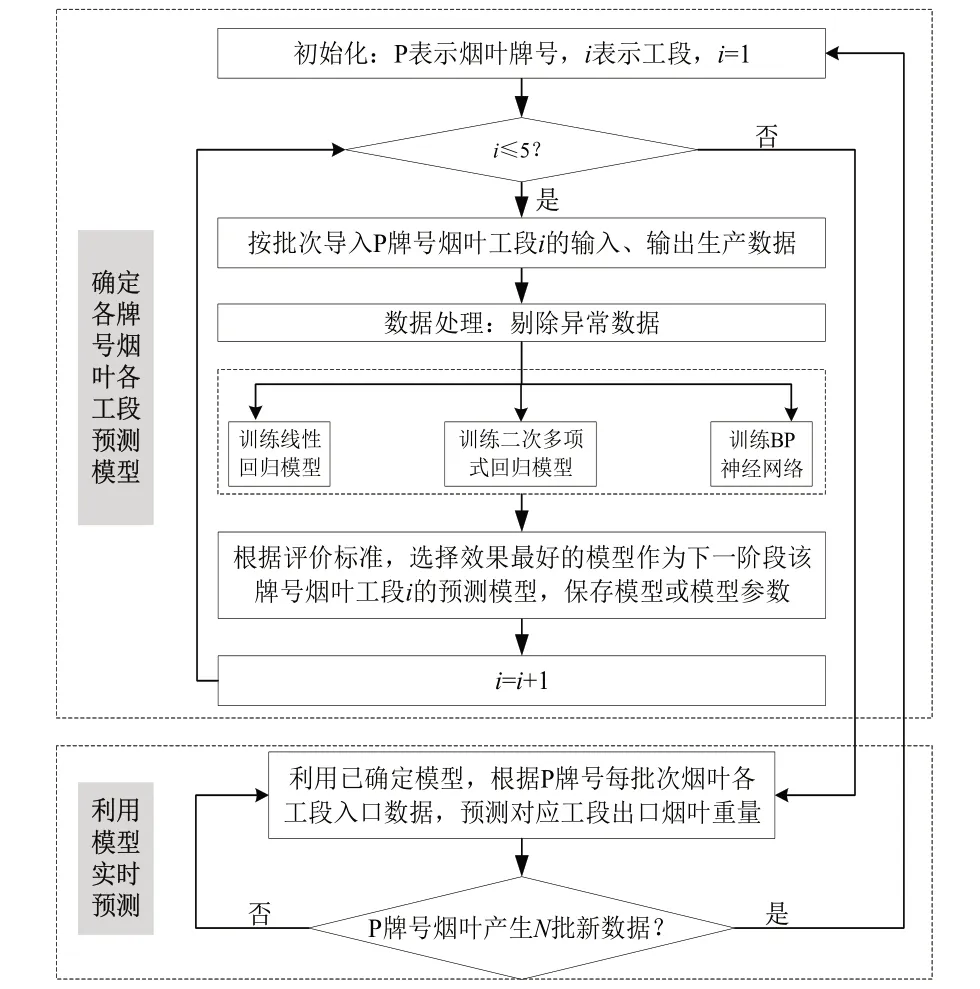
图2 总体建模框架

（1）确定某牌号烟叶各工段预测模型：①导入每一工段的原始输入、输出数据。②剔除异常数据后，将剩余数据作为实验数据。③利用实验数据，分别训练一元线性回归模型、二次多项式回归模型、BP神经网络模型。④利用模型优劣评价标准，对每一工段各模型的运行结果进行评价。选择效果最好的模型作为该工段预测模型，保存模型或模型参数。

（2）利用模型实时预测：①利用各工段已确定的预测模型，根据某牌号烟叶每批次工段入口数据，预测对应出口烟叶重量。②当该牌号烟叶产生N批新数据时，返回第一阶段，更新各工段预测模型。

2.1.2 评价标准。预测精度是指对误差的离散分布情况进行预测，主要取决于模型结构的稳定性、预测数据与实际数值之间的偏差，以及历史数据与参数估计的差距等。预测误差是实际值与理论值之间的离差，主要反映预测的准确度。相关研究证明，均方根误差（RMSE）对预测结果的误差较为敏感，能够很好地反映预测的精密度；平均绝对误差（MAE）能够更好地反映预测值误差的实际情况；平均百分比绝对误差（MAPE）能够直观反映误差占原值的比例。因此，本文采用RMSE作为主要评价标准，同时利用MAE、MAPE进一步分析模型性能。三种误差的计算方法如下：

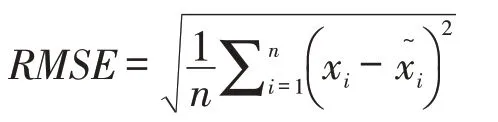
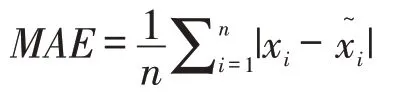
（3）平均百分比绝对误差：

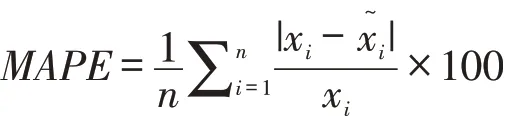
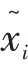
2.2 模型建立

2.2.1 基于回归方法的物料衡算模型

（1）线性回归模型原理。线性回归分析法主要基于数理统计原理，对需要分析的海量数据进行数学建模，并以此得出因变量与多个自变量之间的变动规律，其基本表达形式为。多元回归分析是采用数学模型对因变量与两个或两个以上自变量之间的相关性进行描述，关系表达式如下：

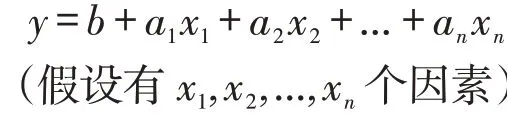
（2）多项式回归模型原理。多项式回归是估计一个因变量与一个或多个自变量间的多项式关系。当因变量与多个自变量存在相关性时，由于线性关系较复杂，此时采用线性回归拟合效果仍需改进。因此，采用多项式回归模型，在此基础上考虑增加特征项，以便拟合非线性数据。一元n次多项式回归方程如下：

（3）模型实验步骤。本文所采用的线性回归及多项式回归模型，主要流程如图3所示，实现步骤具体如下：

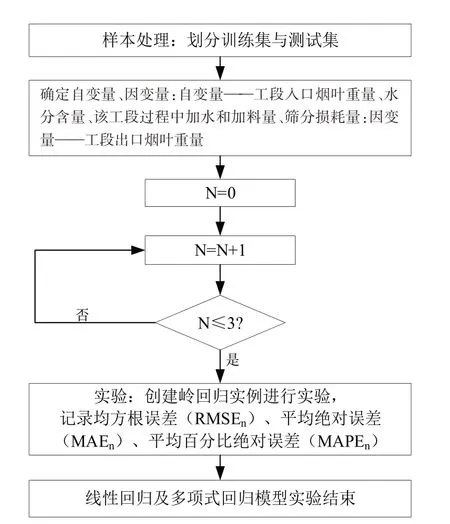
图3 线性回归及多项式回归模型实验步骤

Step1：样本处理。采用随机抽样的方法，将全部样本按照7：3的比例划分为训练集和预测集，执行Step2。

Step2：确定自变量、因变量。根据样本数据选取每一工段对应的自变量为工段入口烟叶重量、水分含量，以及加水或加料量、筛分损耗量，因变量为出口烟叶重量，执行Step3。

Step3：确定多项式次数。多项式次数分别取1、2、3，执行Step4。

Step4：创建回归实例进行实验。将结果可视化处理，并利用均方根误差（RMSE）、平均绝对误差（MAE）、平均百分比绝对误差（MAPE）评估模型效果。

2.2.2 基于BP神经网络的物料衡算模型

（1）BP神经网络模型原理。BP（Back Propagation）神经网络基于有监督的学习机制，将非线性可导函数作为传递函数。BP神经网络能对一系列存在输入-输出模式的数据映射关系进行存储和分析，而无需事先解释其关系。通过反向传播对网络的权值不断调整，以达到误差平方和最小。其算法流程如图4所示，主要由正向传播和反向传播构成：①正向传播：将训练样本的数据输入，然后先沿着网络指向与对应权重相乘后加和，再将结果作为输入并在激活函数中计算，计算结果作为输入传递至下一个节点。依次计算，直到得到最终输出；②反向传播：将输出结果与期望结果进行比较，若所得误差较大，则进一步采用梯度下降法，利用网络结构不断调整各层神经元的权值，该过程本质是一个“负反馈”过程。经过多次迭代，不断调整网络上各个节点间的权重，直到算法终止，利用该模型可进行分析预测。

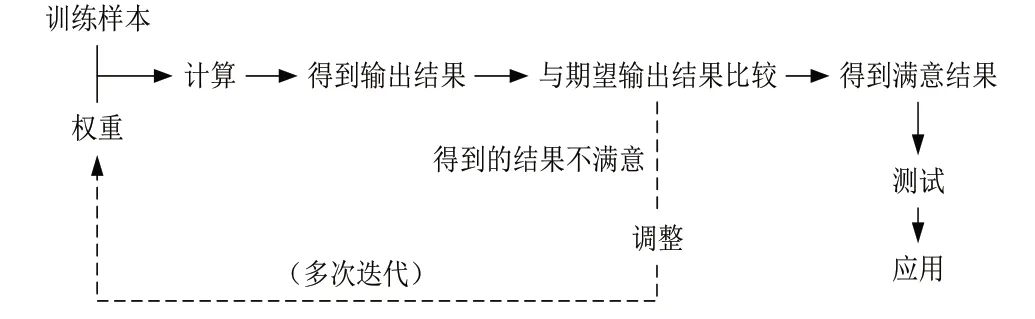
图4 BP神经网络主要过程

（2）模型实验步骤。本文所设计的BP神经网络算法具体实验步骤如下：

Step1：样本处理。采用随机抽样的方法，将全部样本按照7：3的比例划分为训练集和预测集，并对训练集数据进行归一化操作，执行Step2。

Step2：确定网络输入量、输出量。根据样本数据信息，确定每一工段的网络输入量为工段入口烟叶重量、水分含量，以及加水或加料量、筛分损耗量，网络输出量为出口烟叶重量，执行Step3。

Step3：确定网络结构。根据网络输入、输出信息确定网络输入层、隐含层和输出层神经元数目，执行Step4。

Step4：参数初始化。初始化BP网络中每个层级的权值和偏差，同时设定学习率、期望误差最小值、最大迭代次数等一系列基本参数，执行Step5。

Step5：正向传播过程。按照“上层输出矩阵乘当前全连接层参数→加偏置→输入激活函数→输出”的规则完成正向传播过程，执行Step6。

Step6：后向传播过程。使用均方误差计算预估值与实际值的差距，当误差小于期望误差最小值或达到最大迭代次数时，执行Step7；否则，按照误差梯度下降法从后往前逐层调整各神经元的连接权值和偏差，返回Step5。

Step7：算法终止。利用已建立的BP神经网络对测试集进行预测，将结果可视化处理，并利用测试误差评估神经网络效果。

3 实验结果及分析

本文采用Python3.7.8作为编码工具，分别对各个工段利用一次线性回归、二次多项式回归、BP神经网络算法进行实验，并对实验结果进行对比分析，验证三种模型的衡算效果。

3.1 数据来源工段划分

根据制丝加工工艺流程，共包含17道工序，将其划分为6个工段，见表1，本文对前5个工段进行物料衡算。实验数据为某烟厂2021年1月-7月制丝车间生产数据，以一个牌号为例进行测试，共计188条。每条数据包含信息相同，即各工段入口电子秤重量、入口水分含量、过程加料或加水量、过程筛分损耗量和出口电子秤重量。

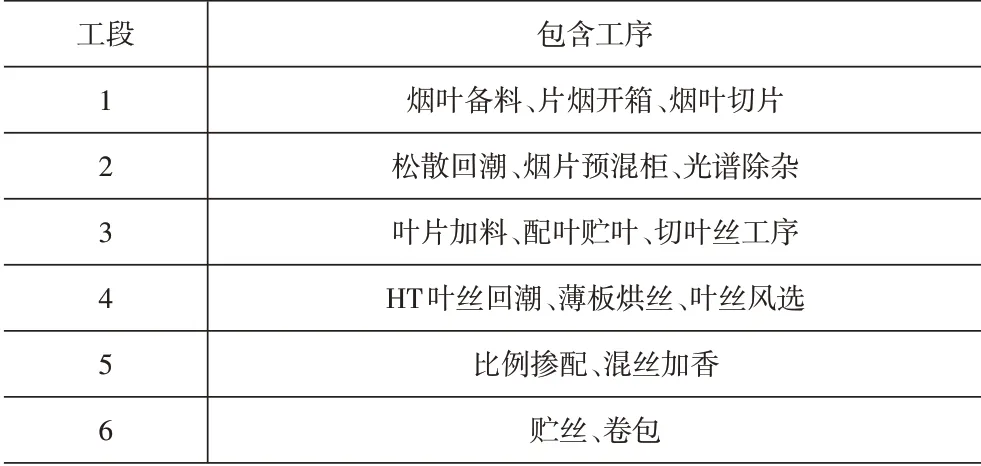
表1 工段划分

3.2 不同工段实验结果

（1）工段一实验结果。该工段设置自变量为“烟叶投料重量”，因变量为“烟叶切片出口重量”。实验结果见表2，结果表明，线性回归模型与多项式回归模型预测结果一致，与BP神经网络预测结果相差不大，但BP神经网络的MAE、MAPE相对较小。

表2 工段一实验结果

（2）工段二实验结果。该工段设置自变量为“松散回潮入口烟叶重量”，因变量为“光谱除杂出口烟叶重量”。实验结果见表3，结果表明，二次多项式回归模型预测结果的RMSE最优，BP神经网络次之，线性回归模型预测结果的RMSE最大。但BP神经网络的MAE和MAPE结果均最优，二次多项式次之，线性回归模型最差。

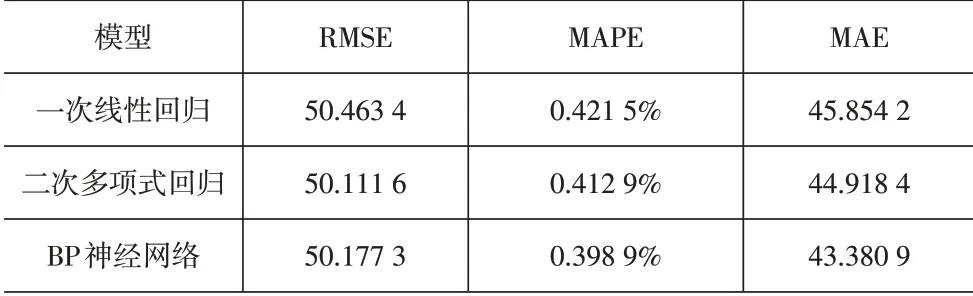
表3 工段二实验结果

（3）工段三实验结果。该工段设置自变量为“叶片加料入口烟叶重量、叶片加料前碎片筛分量”，因变量为“切叶丝工序出口烟叶重量”。实验结果见表4，结果表明，BP神经网络预测结果的RMSE、MAE、MAPE均为最优，线性回归模型次之，二次多项式回归模型预测效果最差。

表4 工段三实验结果

（4）工段四实验结果。该工段设置自变量为“HT入口烟叶重量、HT入口水分、叶丝风选筛分损耗值”，因变量为“叶丝风选出口烟叶重量”。实验结果见表5，结果表明，BP神经网络预测结果的RMSE最小，线性回归模型次之，二次多项式回归模型预测结果的RMSE误差最大，但线性回归模型的MAE、MAPE稍优于BP神经网络。

表5 工段四实验结果

（5）工段五实验结果。该工段设置自变量为“掺配入口叶丝主秤实际重量、混丝加香前筛分损耗值”，因变量为“混丝加香入口重量”。实验结果见表6，结果表明，二次多项式回归结果明显优于一次线性回归结果和BP神经网络模型。

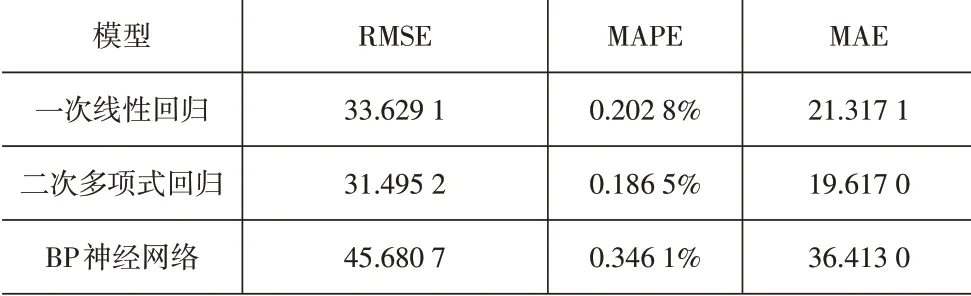
表6 工段五实验结果

3.3 实例测试结果分析

根据以上实验结果可知，（1）选取三种模型进行预测具有一定合理性，平均百分比绝对误差（MAPE）最高仅为0.605 5%。（2）从工段分析，工段一和工段二的预测精度明显高于后三个工段。主要原因是：工段一和工段二包含工序相对较少，且工序处理过程较为简单，不涉及过多的加水、加料、筛分、烘干等对烟叶重量影响较大的环节。因此，输入与输出数据的关系更容易拟合。同时，观察结果可知，工段二和工段四输入输出数据的线性关系相对显著。（3）从模型分析，一次线性回归模型在该制丝生产线中表现最好，BP神经网络与其预测效果相差不大，二次多项式回归模型在工段五中表现较好。综上，对于所选取牌号的物料衡算模型，工段一应采用一次线性回归，工段二和工段五应采用二次多项式回归；工段三和工段四应采用BP神经网络。

4 结语

目前，我国烟草制丝工艺大部分实现了自动化、机械化生产，但离智能制造仍存在一定距离。在机器学习、数据挖掘等先进技术日趋成熟的背景下，本文采用自适应的大数据建模技术，研究制丝工艺中关键工序的物料进出衡算方法，构建全流程物料衡算模型。首先，通过对制丝工艺主要流程和影响因素进行分析，确定物料流量监控点及监控要素；然后，基于工艺流程将制丝过程划分为不同工段，分别采用线性回归、多项式回归及BP神经网络对不同工段数据进行模型拟合；最后，根据三种评价指标分析实验结果，为每个工段选取较优的物料衡算模型，并对产生预测误差的原因进行深入分析。本文研究成果可完善制丝全流程物料计量体系，为卷烟生产的自动排产和智能生产提供支撑，同时为建设数字化工厂，实现精益生产提供参考和借鉴。