初始剪应力与振动频率对饱和粘土动强度特性影响研究
2022-09-13曹久亭黄思杰
张 健,曹久亭,黄思杰
(1.南京交通职业技术学院,江苏 南京 211188;2.江苏中设集团股份有限公司,江苏 无锡 214072;3.交通运输部天津水运工程科学研究所,天津 300456)
0 引言
我国是一个地震多发的国家,地震区域分布广阔,西南地区地震尤为强烈。百年来,我国发生过强震(M≥8)的次数已达10 次之多,其中人口居住密集之处,人口伤亡和财产损失严重[1-3]。1920 年发生在宁夏的海原地震死亡人数多达20 余万;1976 年河北唐山7.8 级大地震造成24 万余人罹难;2008 年四川汶川8.0 级特大地震,最大烈度达11 度,遇难和失踪达到8万余人[4-5]。对于我国这样一个地震多发国家而言,许多修建在软黏土地基上的建筑物、构筑物都有可能遭遇地震,而这些软黏土地基上不可避免地存在初始剪应力作用[6-7],在初始剪应力的作用下,软黏土会展现出不同的动力特性[8-10]。因此有必要对初始剪应力作用下软黏土动强度特性进行研究,研究成果具有很强的应用价值。
目前,大部分试验主要考虑不存在初始剪应力的状态,即三向均等固结压力而展开试验的。初始剪应力是影响饱和粘土动力特性的一个重要因素,越来越多的研究人员开始关注研究初始剪应力作用。
Yasuhara 等[11]认为正常固结粘土在循环荷载作用下,土体内部孔隙水压力随振动次数增加而逐渐上升,从而引起土体有效应力降低,动强度逐渐降低,且残余孔压越大,土体动强度衰减程度越高。Ishihara 等[12]研究表明初始剪应力的存在将会提高土体的总强度。Seed 等[13]、Zimmie 等[14]和Goulois 等[15]均认为土体的抗剪强度随着初始剪应力的增加而逐渐降低。Lefebvre等[16]通过试验指出,土体存在初始剪应力时,在降低抗剪强度的同时会提高土体的总强度。而Tan 等[17]研究认为,随着初始剪应力的增大,粘土动强度逐渐降低。Matisui 等[18]通过粘土循环三轴试验发现,当循环应力比较大时,土体的剪切强度将有所降低。
廖红建等[19]通过对火山灰粘性土进行循环三轴试验认为,固结比对火山灰粘性土的动剪强度有显著影响,并建立关于固结比变化的动剪强度表达式。黄博、陈云敏等[20]在研究循环荷载作用下海洋粘性土动力特性时指出,在同一动应力水平下,振动频率越高,土体动强度越高;土体天然结构性决定了不同频率下土体动强度的差异,即使振动次数达到较高水平,频率对动强度仍产生显著影响。潘林有等[21]通过对杭州原状软粘土进行循环三轴试验,结果表明:低频时土体的动强度随着振动频率的增大而增大,但振动频率超过2Hz 后,土体动强度增加的幅度出现逐渐减小的现象。而张茹等[22]通过试验分析指出,饱和粘土不同振动频率条件下动强度曲线存在拐点,在拐点之前,土体动强度随频率提高而增加,但是在拐点之后,土体动强度随着频率提高出现降低的现象。
由上述分析可知,众多基础设施均修建在广泛分布的软黏土地基之上,而这些地基上不可避免的存在初始剪应力的作用[23-25]。而目前初始剪应力和振动频率对饱和粘土动强度特性的影响并未得到一致的结论,尚未建立不同初始剪应力条件下动强度与振次的关系。饱和粘土动强度与破坏标准选取密切相关,而目前对于破坏标准的选取尚未明确,也未能给出不同震级下软黏土强度参数(c、φ)的变化规律。因此很有必要继续开展饱和粘土动强度特性试验研究,从而为地震荷载作用下粘土地基稳定性分析提供理论基础。
1 试验土样及方案
1.1 试验土样
本文试验所用粘土取自四川汶川,取样深度约为4~6m,为重塑粘土。粘土基本物理性质如表1 所示。根据粘性土分类标准,利用塑性图对汶川震区粘土进行分类,试验所用粘土为粘性低塑性土。

表1 粘土基本物理性质指标
1.2 试验过程与方法
本次试验使用DDS-70 型动三轴仪。试验采用直径39.1mm,高度为80mm 的重塑土样。重塑试样的制备方法为多层湿捣法,分5 层击实,根据土样的干密度和预先设计的含水量确定每层土样的重量,击实到相应高度,各层接触面刮毛以保证上下接触良好。在三轴压力室内联合抽真空、通无气水和加反压两种方法饱和,当孔隙水压力系数B 值≥0.97 时,认为试样满足饱和度要求。然后进入固结阶段,试样饱和完成后,将排水阀缓慢打开,当孔压消散接近0 时,此时关闭排水阀5 分钟,若孔隙水压力不再上升,认为固结完成。当偏压固结时,等压固结完成后,再逐渐增加偏应力,此时要打开排水阀,避免产生变形破坏,当施加到相应的偏应力,固结一段时间,关闭排水阀,完成偏压固结过程。
1.3 试验方案
根据取土深度及研究需要,试验固结围压采用σc=50kPa、σc=100kPa 和σc=150kPa。由于地震作用提供的循环荷载作用时间短,粘土层排水慢,可视为土体处于不排水状态,故试验采用不排水剪。根据地震荷载频率范围,振动频率采用f=1Hz、f=2Hz 和f=4Hz;本文定义动应力幅值σd与2 倍围压σc的比值为动应力比r,即:

试验动应力比分别采用r=0.165,r=0.25,r=0.335;为考虑初始剪应力对饱和粘土动力特性影响,分别进行了固结比Kc=1、Kc=1.25 和Kc=1.5 的循环三轴试验,其中:
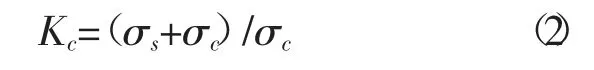
式中,σs表示初始剪应力,σc表示固结围压,Kc的大小反映了土体的初始剪应力水平。
由于地震荷载具有不对称和不规则的特点,不可能重复发生地震波波形相同的地震,因此本文输入的地震荷载采用等幅波形的正弦波进行模拟。具体试验方案如表2 所示。
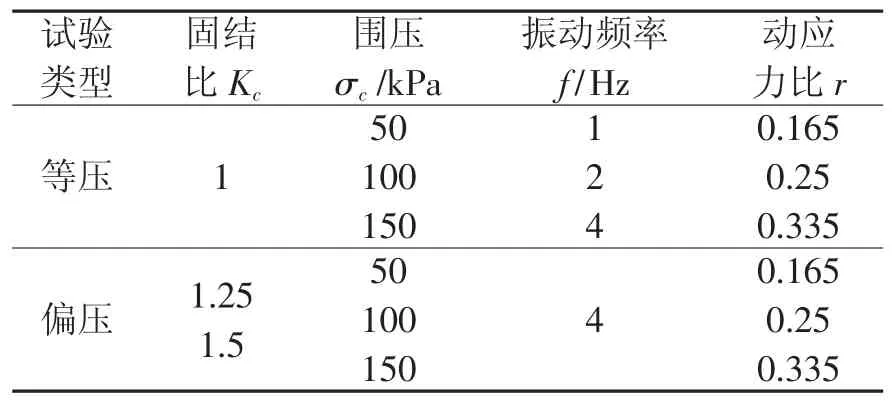
表2 饱和粘土循环三轴试验方案
2 饱和粘土动强度破坏标准的确定
2.1 饱和粘土动强度破坏标准
对于饱和粘土来说,由于土体内部排水条件差,孔隙水压力测试出现滞后现象,所以通常选取应变破坏标准。为达到土体应变的破坏标准,通常有两种办法,可以选取较大的动应力而减少循环作用次数;或者选取较小的动应力而增加循环作用次数。本文将选取εp=2.5%,εp=5%和εp=εtp三种情况来开展饱和粘土动强度破坏标准研究。通过试验数据对比选取合适的破坏标准,定量分析三种破坏标准条件下饱和粘土动强度的差异性。
2.2 饱和粘土动强度曲线
土体动强度表示为达到破坏标准时的循环振动次数N 与动应力σd的关系,即σd-N 曲线,称为土体动强度曲线。通过对一组不同围压的循环三轴试验,就可以得到一组莫尔应力圆。通过求解这一组莫尔应力圆公切线的截距和斜率,即可获得该振动次数下土体动强度参数动粘聚力cd和动内摩擦角φd,如图1 所示。
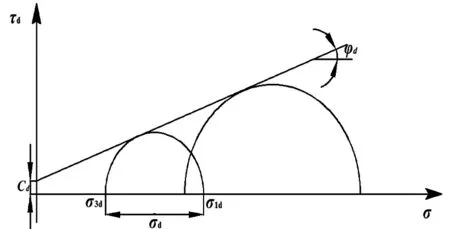
图1 土体动强度莫尔应力圆Fig.1 Mohr stress circle of soil dynamic strength
2.3 应变破坏标准对饱和粘土动强度的影响
由土体动强度的定义可知动强度与应变破坏标准存在密切联系,选取合适的应变破坏标准关系到能否真实的反映土体破坏情况。图2所示为试样在围压σc=100kPa,振动频率f=4Hz,固结比Kc=1,应变破坏标准分别为εp=εtp,εp=2.5%和εp=5%时饱和粘土的动强度曲线。

图2 不同应变破坏标准下土体动强度曲线Fig.2 Dynamic strength curves of soil under different strain failure criteria
由图中可以看出,随循环振动次数增加,土体的动强度逐渐降低。另外,动强度曲线存在拐点,在拐点之前,关系曲线较陡峭,即振动次数较低时切线斜率较高,说明此时土体动强度衰减较快;在拐点之后,关系曲线逐渐平缓,即随着振动次数增加,关系曲线切线斜率逐渐降低,说明此时动强度衰减趋于缓慢。
由图2 可以看出,应变破坏标准对土体的动强度分析有明显影响,提高应变破坏标准,将会人为的提高土体动强度。相同动应力条件下,应变破坏标准越高,土体达到破坏所需的振动次数越多。相同振动次数条件下,应变破坏标准越高,土体达到破坏所需的动应力越大。图中在较低振动次数下εp=2.5%与εp=εtp对应的土体动强度-振动次数曲线比较接近,这说明选用应变破坏标准εp=2.5%与εp=εtp能比较真实的反应土体破坏情况,对土体动强度安全评价更为客观。而采用应变破坏标准εp=5%往往不能反映土体真实的破坏情况,会高估土体的动强度,并且振动次数越多,这种现象越明显。
2.4 应变破坏标准的确定
由于土体动强度与循环振动次数存在必然的联系,在进行地震荷载作用下土体动强度分析时需要引入等效破坏振次这个概念。
循环三轴试验中循环荷载采用的波形往往具有一定的规律性,比如本文采用的等幅正弦波形,这与实际情况中地震荷载引起的振动波形有很大差异。因此,为减少两种荷载之间对土体作用的差异性,在分析土体动强度时,根据《地基动力特性测试规范》,必须使用等效破坏振次Nf来代替试验过程中循环荷载的振动次数,并且指出等效破坏次数与震级有关,对应关系如表3 所示。

表3 地震震级-等效破坏振次对应关系
2.5 地震荷载作用下饱和粘土应变破坏标准
基于上一小节的分析可以看出应变破坏标准的不同将对土体动强度产生重要影响。本小节将开展不同应变破坏标准下饱和粘土动强度参数定量研究,以便说明选取合适应变破坏标准的重要意义。由于只有在较低振动次数下εp=εtp与εp=2.5%对应的土体动强度-振动次数曲线比较接近,本文将在考虑振动次数范围较广的条件下,选取εp=2.5%和εp=εtp两种情况进行土体动强度参数分析。
图3 所示为试验条件固结比Kc=1,振动频率f=1Hz,围压分别为σc=50kPa、σc=100kPa 和σc=150kPa 时饱和粘土应变破坏标准为εp=2.5%的动强度曲线。可以发现,动强度曲线在对数坐标中近似成一条直线,即在对数坐标中动应力与振动次数呈线性关系,因此,本文假设动应力-振动次数关系表达式为:

图3 εp=2.5%时饱和粘土动强度曲线Fig.3 Dynamic strength curve of saturated clay when εp=2.5%

其中a,b 为与试验条件有关的常数。通过对图中不同围压下的动强度曲线进行拟合得:
σc=50kPa 时,σd=-3.89lnN+40.40
σc=100kPa 时,σd=-17.61lnN+96.05
σc=150kPa 时,σd=-20.16lnN+127.85
然后计算出不同地震震级对应的等效破坏振次所需的动应力,进而计算得到不同等效破坏振次下土体的动粘聚力cd和动内摩擦角φd,计算结果如表4 所示。

表4 εp=2.5%时各等效破坏振次下土体动强度参数
图4 所示为试验条件固结比Kc=1,频率f=1Hz,围压分别为σc=50kPa、σc=100kPa 和σc=150kPa 时饱和粘土应变破坏标准为εp=εtp的动强度曲线,仍然假设对数坐标中动应力与振动次数呈线性关系。
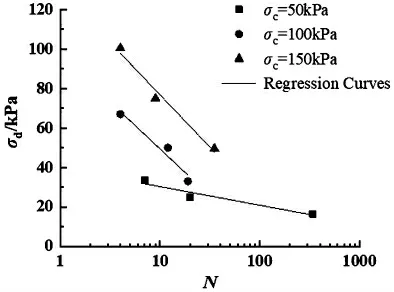
图4 εp=εtp 时饱和粘土动强度曲线Fig.4 Dynamic strength curve of saturated clay when εp=εtp
通过对图4 中不同围压下的动强度曲线进行拟合得:
σc=50kPa 时,σd=-4.09lnN+39.68
σc=100kPa 时,σd=-20.66lnN+96.94
σc=150kPa 时,σd=-23.02lnN+129.79
计算出εp=εtp时不同等效破坏振次下土体的动粘聚力cd和动内摩擦角φd,计算结果如表5 所示。
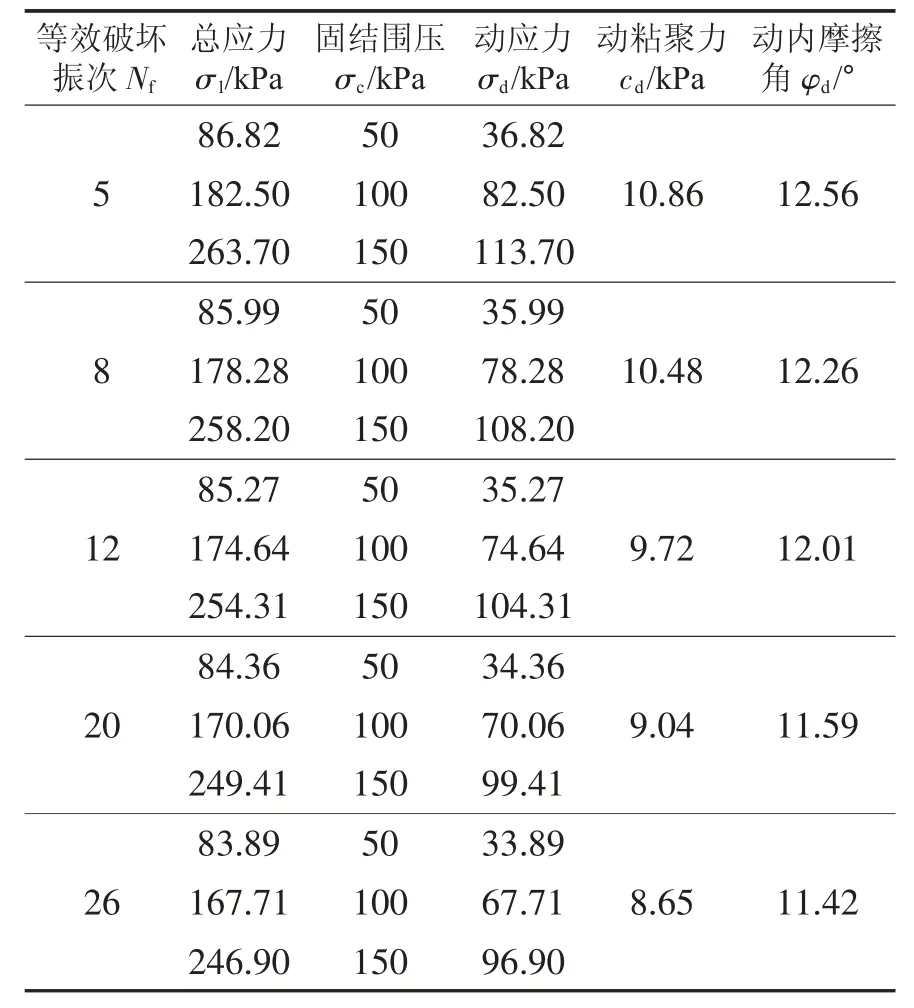
表5 εp=εtp 时各等效破坏振次下土体动强度参数
图5 所示为εp=εtp和εp=2.5%时饱和粘土动强度参数cd和φd与等效破坏振次Nf的关系曲线。
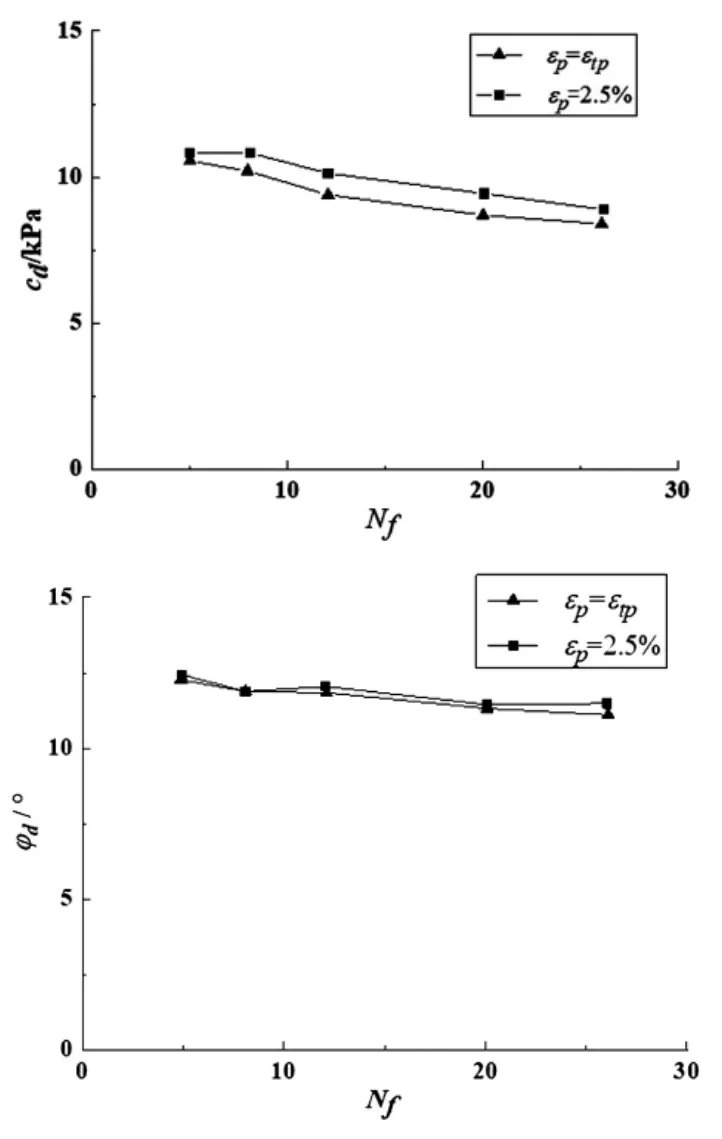
图5 不同破坏标准时cd-N、φd-N 关系曲线Fig.5 Cd-N、φd-N relationship curve under different damage standards
从图5 中可以发现,在应变破坏标准分别为εp=εtp与εp=2.5%时对应的土体动强度参数cd和φd与等效破坏振次Nf的关系曲线比较接近。因此,可以说明在较低振动次下选取应变破坏标准为εp=εtp与εp=2.5%时计算得到的土体动强度参数cd和φd的值相差不大。另外由于转折应变εtp的值具有一定的不确定性,因此本文建议计算地震荷载等效破坏振次下的饱和粘土动强度参数,可以使用εp=2.5%来代替εp=εtp。
3 试验结果与分析
3.1 初始剪应力对饱和粘土动强度特性的影响
图6 所示为土体应变破坏标准εp=2.5%,围压σc=100kPa,振动频率f=4Hz,固结比分别为Kc=1、Kc=1.25 和Kc=1.5 时饱和粘土动强度曲线。从图中可以看出,初始剪应力对饱和粘土的动强度有显著影响。相同动应力时,初始剪应力越大,土体达到应变破坏标准所需的振动次数越少,土体动强度越低;相同振动次数条件下,初始剪应力越大,土体达到应变破坏标准所需的动应力越小。可以解释为:初始剪应力较小时,其对土体起到预压作用,从而起到提高土体动强度的作用;而初始剪应力较大时,破坏了粘土内部颗粒间的粘结,从而起到降低粘土动强度的作用。同样可以看出,土体动强度曲线存在一个拐点,初始剪应越小,拐点之后的动强度曲线越平缓,曲线切线斜率越小。
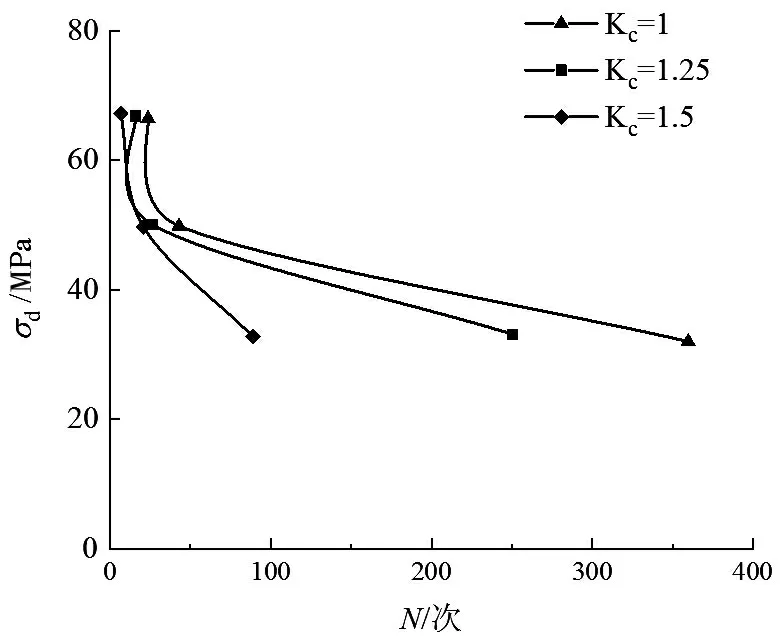
图6 不同初始剪应力下饱和粘土动强度曲线Fig.6 Dynamic strength curve of saturated clay under different initial shear stress
3.2 初始剪应力对饱和粘土动强度参数的影响
由以上分析可以得知,初始剪应力对饱和粘土动强度有明显影响,本节将通过对饱和粘土动强度参数进行定量分析,研究初始剪应力对动强度参数的影响。图7 所示为试验条件固结比Kc=1,频率f=4Hz,应变破坏标准εp=2.5%,围压分别为σc=50kPa、σc=100kPa 和σc=150kPa时饱和粘土动强度曲线。
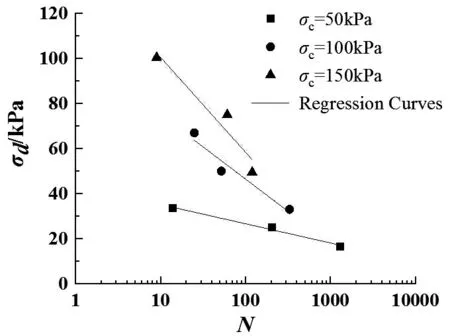
图7 Kc=1 时饱和粘土动强度曲线Fig.7 Dynamic strength curve of saturated clay when Kc=1
利用公式(1)对不同围压下动强度曲线进行回归分析得:
σc=50kPa 时,σd=-3.71lnN+43.69
σc=100kPa 时,σd=-12.40lnN+103.63
σc=150kPa 时,σd=-18.36lnN+142.82
然后计算出不同地震震级对应的等效破坏振次所需的动应力,进而计算出不同等坏振次下土体的动粘聚力cd和动内摩擦角φd,计算结果如表6 所示。
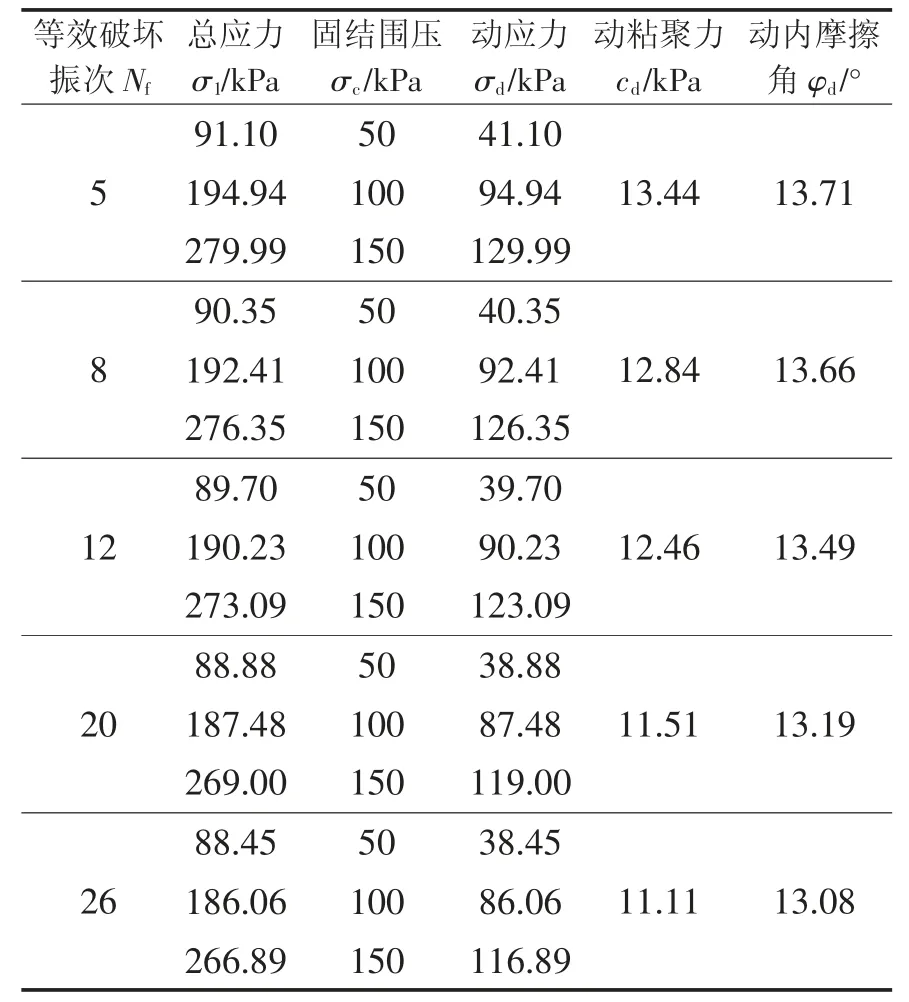
表6 Kc=1 时各等效破坏振次下土体动强度参数
图8 所示为试验条件固结比Kc=1.25,频率f=4Hz,应变破坏标准εp=2.5%,围压分别为σc=50kPa、σc=100kPa 和σc=150kPa 时饱和粘土动强度拟合曲线。

图8 Kc=1.25 时饱和粘土动强度曲线Fig.8 Dynamic strength curve of saturated clay when Kc=1.25
利用公式(1)对不同围压下动强度曲线进行回归分析得:
σc=50kPa 时,σd=-4.49lnN+43.46
σc=100kPa 时,σd=-11.87lnN+97.03
σc=150kPa 时,σd=-17.08lnN+132.98
然后计算出不同地震震级对应的等效破坏振次所需的动应力,进而计算出不同破坏振次下土体的动粘聚力cd和动内摩擦角φd,计算结果如表7 所示。
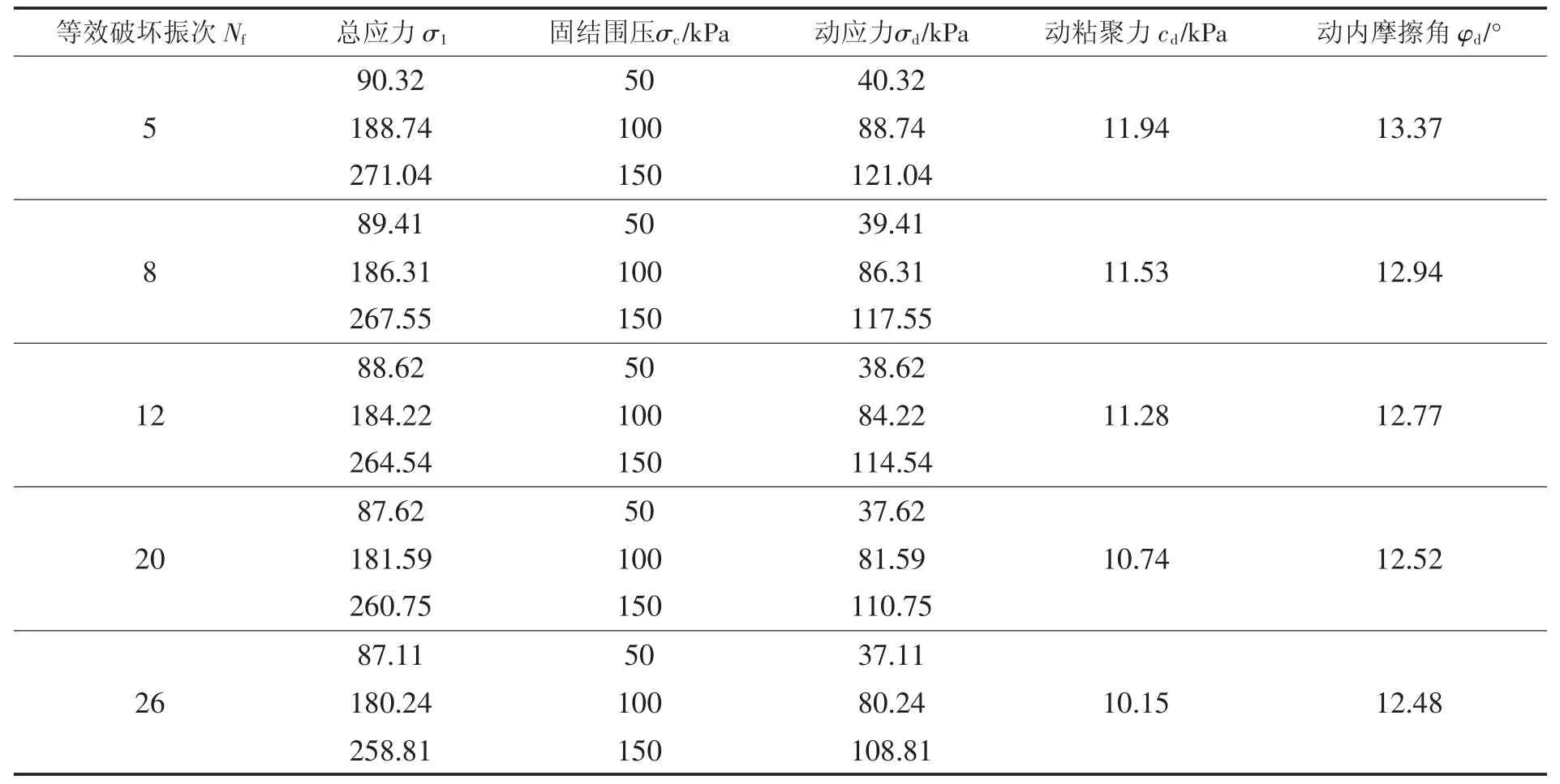
表7 Kc=1.25 时各等效破坏振次下土体动强度参数
图9 所示为试验条件固结比Kc=1.5,频率f=4Hz,应变破坏标准εp=2.5%,围压分别为σc=50kPa、σc=100kPa 和σc=150kPa 时饱和粘土动强度曲线。

图9 Kc=1.5 时饱和粘土动强度曲线Fig.9 Dynamic strength curve of saturated clay when Kc=1.5
利用公式(1)对不同围压下动强度曲线进行回归分析得:
σc=50kPa 时,σd=-5.36lnN+43.62
σc=100kPa 时,σd=-14.521lnN+96.82
σc=150kPa 时,σd=-19.18lnN+130.67
然后计算出不同地震震级对应的等效破坏振次所需的动应力,进而计算出不同破坏振次下土体的动粘聚力cd和动内摩擦角φd,计算结果如表8 所示。

表8 Kc=1.5 时各等效破坏振次下土体动强度参数
图10 所示为不同初始剪应力下饱和粘土动强度参数cd和φd与等效破坏振次Nf的关系曲线。

图10 不同初始剪应力下土体cd-Nf、φd-Nf 关系曲线Fig.10 Soil cd-Nf、φd-Nf relationship curve under different initial shear stress
从图10 中可以看出,饱和粘土动强度参数受到初始剪应力的影响,表现为初始剪应力越大,土体动强度参数越小,说明初始剪应力的存在降低了土体动强度。因此,在工程抗震设计中,应充分重视初始剪应力对饱和粘土的影响。
3.3 振动频率对饱和粘土动强度特性的影响
图11 所示为土体应变破坏标准εp=2.5%,围压σc=100kPa,固结比Kc=1,振动频率分别为f=1Hz、f=2Hz 和f=4Hz 时饱和粘土动强度曲线。从图中可以看出,振动频率对土体的动强度有影响,相同动应力条件下,振动频率越高,土体达到破坏所需的振动次数越多,说明土体动强度越大;相同振动次数条件下,振动频率越高,土体达到破坏所需的动应力越大。可以解释为:在低频循环荷载作用下,孔隙水压力有足够时间上升,导致土样在较小的循环次数发生破坏。而在高频循环荷载作用下,软粘土的孔隙水压力来不及上升,根据有效应力原理,土体的有效应力越高,抗剪强度越高。另外从图中可以发现,在动强度曲线拐点之后,振动频率越高,曲线越平缓,曲线切线斜率越小。
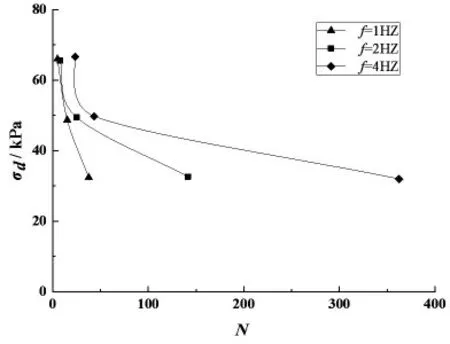
图11 εp=2.5%时不同振动频率下土体动强度曲线Fig.11 Dynamic strength curve of soil under different vibration frequencies when εp=2.5%
3.4 振动频率对饱和粘土动强度参数的影响
由以上研究可以发现,饱和粘土动强度受振动频率影响。通过对地震荷载作用下等效破坏动强度参数进行定量分析,研究振动频率对动强度参数的影响。图12 所示为试验条件振动频率f=2Hz,固结比Kc=1,应变破坏标准εp=2.5%,围压分别为σc=50kPa、σc=100kPa 和σc=150kPa时饱和粘土动强度曲线。
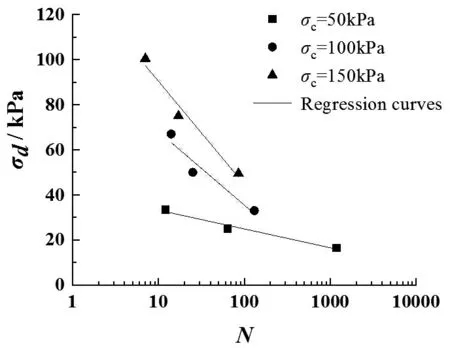
图12 f=2Hz 时饱和粘土动强度曲线Fig.12 Dynamic strength curve of saturated clay when f=2Hz
利用公式(3)对不同围压下动强度曲线进行回归分析得:
σc=50kPa 时,σd=-3.61lnN+41.53
σc=100kPa 时,σd=-14.17lnN+100.66
σc=150kPa 时,σd=-19.87lnN+136.09
然后可以计算出不同地震震级对应的等效破坏振次所需的动应力,进而计算出不同等效破坏振次下土体的动粘聚力cd和动内摩擦角φd,计算结果如表9 所示。

表9 f=2Hz 时各等效破坏振次下土体动强度参数
振动频率f=1Hz 时饱和粘土等效破坏动强度参数见表4。振动频率f=4Hz 时饱和粘土等效破坏动强度参数见表6。振动频率f=2Hz 时饱和粘土等效破坏动强度参数见表9。
图13 所示为不同振动频率下饱和粘土动强度参数cd和φd与等效破坏振次Nf的关系曲线。由图中可以看出,饱和粘土动强度参数受到荷载振动频率的影响,表现为振动频率越低,土体动强度参数越小。

图13 不同振动频率下饱和粘土cd-N、φd-N 关系曲线Fig.13 Saturated clay cd-N、φd-N relationship curve under different vibration frequencies
4 结论
通过动三轴试验系统,对汶川地区饱和黏土动强度特性进行试验研究。首先,基于土体动强度定义,分析了不同应变破坏标准的影响,在试验数据基础上确定了合适的应变破坏标准。然后,计算了汶川震区饱和粘土在地震荷载等效破坏振次下的动强度参数。最后,研究了初始剪应力和振动频率对饱和粘土动强度的影响。得到如下结论:
(1)通过对不同应变破坏标准下的饱和粘土动强度进行定性及定量研究,均表明选用应变破坏标准为应变值2.5%与转折应变对土体动强度安全评价更为客观。并指出计算地震荷载等效破坏振次下的饱和粘土动强度参数,可以使用εp=2.5%来代替εp=εtp。
(2)通过对饱和粘土动强度参数定量研究指出,随循环振动次数增加,土体的动强度参数逐渐减小,表明土体的动强度逐渐降低。
(3)通过引入地震荷载下土体等效破坏振次,给出了不同地震震级下汶川震区饱和粘土动强度参数。
(4)初始剪应力对饱和粘土的动强度有较大的影响。相同振动次数下,初始剪应力越大,土体达到破坏所需的动应力越小,动强度参数也越小,说明初始剪应力的存在降低了土体动强度。
(5)振动频率对饱和粘土的动强度有较大的影响。相同振动次数下,振动频率越高,土体达到破坏所需的动应力越大,动强度参数也越大,说明土体动强度越大。
