基于WPD-LPF和灰色关联度的混合储能平抑风电波动控制策略

王苏蓬，张新慧，张 军，白文渊

（山东理工大学 电气与电子工程学院，山东 淄博 255000）

0 引言

风电出力具有间歇性、随机性的特点，风电直接并网会影响电力系统的稳定安全运行[1]。混合储能技术可以平抑风电波动，改善风电出力特性，提高风电利用率。目前针对平抑风电波动算法和储能系统能量控制策略方面的研究仍不太成熟。

国内外针对储能系统容量配置方法的研究较多[2]，其中低通滤波法、经验模态分解（Empirical Mode Decomposition，EMD）、集合经验模态分解（Ensemble Empirical Mode Decomposition，EEMD）、变分模态分解 （Variational Mode Decomposition，VMD）、小 波 包 算 法（Wavelet Packet Decomposition，WPD）在风电功率平滑处理上得到广泛应用。为解决采用传统低通滤波法进行储能功率分配时其截止特性差的问题，文献[3]提出了基于二阶滤波的混合储能系统功率分配方法。该算法在进行中存在一定的时延，且时间常数选取困难，这些因素会导致混合储能系统配置不合理。文献[4]采用滑动平均法和EMD进行储能功率的分配，以全生命周期下储能系统净收益最大为目标，进行储能容量的配置。为解决EMD分解本身存在边界效应和模态混叠问题，文献[5]在采用EMD分解风电功率时，引入白噪声解决模态混叠问题，但该方法在进行信号重构会存在噪声分量，使重构信号与原信号产生较大偏差。文献[6]采用滑动平均法以及VMD结合希尔伯特变换进行储能功率的划分，能够有效解决频谱混叠，但在采用VMD时，分解模态数和二次惩罚因子对信号重构具有较大影响，上述两个变量难以选择。小波包分解可以更好的处理局部突变信号，且不存在边界效应和模态混叠等问题，使得小波包算法在风电功率平滑处理上得到广泛应用。文献[7]采用小波包分解风电功率，设置内外层目标函数，采用元模型优化算法进行容量配置求解。文献[8]提出一种确定小波包最优分解层数的方法，采用db6小波对风电功率进行分解，利用模糊控制对储能功率进行修正，实现风电功率平抑。上述基于WPD的混合储能平抑风电波动控制策略皆以最优分解层数下的低频功率分量作为并网功率。该风电并网功率获取方法存在以下问题。当某一分解层数下存在某几个时段低频功率分量波动率超过并网要求时，虽然通过加大分解层数可以使上述某几个时段低频功率分量的波动率下降，但其他时段的低频功率分量波动率也会随之减小，致使该最优分解层数下的低频功率分量过于平滑。基于该分解结果下风电并网功率分量信息不足，对储能的容量配置要求更高。

本文首先采用小波包分解风电功率，在满足并网要求前提下，为获取更多风电并网功率分量信息，以风电并网功率波动限值作为选取滤波最优截止频率指标，引入低通滤波（Low Pass Filter，LPF）对高频功率分量进一步分解，获取所需的部分高频功率分量信息。上述两部分功率分量总和作为风电并网功率。为避免人为确定混合储能功率的分界点和缩短计算时间，利用灰色关联度聚类 重 构（Grey Relational Grades Cluster，GRGC）剩余的各高频分量，确定混合储能功率的分界点，获得混合储能功率曲线。最后利用模糊控制对混合储能功率修正，得到优化后的混合储能功率分配指令。

1 基于WPD-LPF的风电功率分解

为获取更多的风电并网功率分量信息，利用WPD-LPF分解原功率信号获取风电并网功率。小波包算法具有处理局部突变信号的优势[9]，一阶低通滤波法具有原理简单、实用性强的特点，但无法做到局部突变信号的处理[10]。结合两种算法优势，首先采用小波包分解风电功率，处理相应的局部突变信号，获得低频功率分量P0和高频功率分量Pgp；其次利用一阶低通滤波算法对高频分量的 第 一 个 频 段Pw（wb，21）进 一 步 分 解，获 取 所 需 的风电并网功率分量（t）；最终风电并网功率由上述两部分功率分量组成。基于WPD-LPF的风电功率分解如图1所示。

图1 WPD-LPF分解风电功率控制框图Fig.1 Control block diagram of WPD-LPF decomposition of wind power

1.1 风-储联合系统拓扑图

为减小风电波动，实现风电安全可靠并网，须要为风电配置混合储能系统。通常选取蓄电池和超级电容分别代表能量型、功率型储能介质组成混合储能系统 （Hybrid Energy Storage System，HESS）平抑风电功率波动[11]。由风电、混合储能系统组成的风-储联合系统拓扑如图2所示。图中：Pw为风电实际出力；Pb为经储能平滑的风电 功 率；PHess为 混 合 储 能 系 统 功 率；Pgl，Pnl分 别 为超级电容、蓄电池的功率。

图2 风-储联合系统拓扑图Fig.2 Topology of wind-energy storage hybrid systems

由图2可得各参数关系为

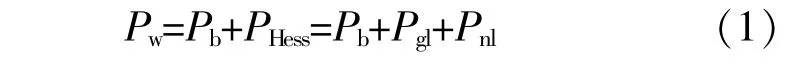
1.2 小波包方法分解风电功率

小波包分解风电功率，分别得到低频、高频功率分量为

式中：P0，Pgp分别为经小波包分解的风电低频、高频功率分量；Pw（.）为小波包分解风电功率各频段重构后对应的功率；wb为小波包分解的小波基；n为最优分解层数；20:2n为从20～2n的频带区间。式中低频功率分量满足国标要求，可直接并网，对于高频功率分量需要采用混合储能进行平抑。

在采用小波包分解风电功率时，主要存在最优分解层数确定、小波基选取困难问题。综合考虑离散小波基的正交性、对称性和紧支撑性，本节选用满足条件的coif，sym和db小波为研究对象。风电功率信号分解的准确度、稳定性随着小波基函数消失矩减小而减小。当消失矩较大时，风电功率分解时间会大大增加[12]。综合考虑后，本文剔除sym和db小波在较低和较高消失矩的实验数据，并采用文献[13]最优小波基选择方法，以WPD分解风电功率耗时的重构信号误差e为指标，其表达式为

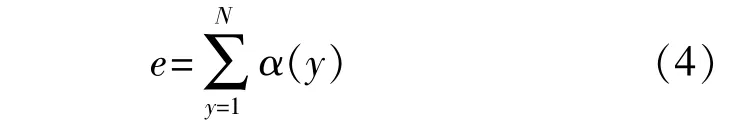
小波基选取得到实验结果如图3所示。

图3 3种小波基实验结果Fig.3 Experimental results of three wavelet bases

由图3可知，coif小波总体耗时短但误差较大，难以正确处理本文所述风电信号。sym20的误差为54，耗时0.42s，尽管误差相对较小，但运算时间长，不利于实时处理风电功率信号。db小波的整体耗时小，其误差为58，耗时0.143s，适合处理此类本文所述风电信号。因此，选择db6作为最优小波基。

利用小波包分解风电功率，以n为循环变量，计算每个分解层数下低频分量的功率波动ΔP，是否满足表1所示现行国家标准规定的风电场有功功率变化的最大限值。当ΔP满足并网要求，停止循环，否则继续加深分解层数n，进而确定小波包最优分解层数[8]。

表1 并网时风电场有功功率变化的最大限值Table1Maximum limit of active power change of wind farms when connected to the grid

低频分量的功率波动ΔP为

式 中：P0max，t1和P0min，t1分 别 为 以10min为 时 间 尺 度下,低频功率分量的最大值和最小值；t1为以10 min为 时 间 尺 度 段 数，t1=1，2……T/600，T为 采 样总时长。

1.3 低通滤波法分解风电高频分量

利 用 一 阶 低 通 滤 波 算 法 对Pw（wb，21）进 一 步分解，获得所需的风电并网功率分量（t）。一阶低通滤波传递函数为

式中：fc为滤波器截止频率；Ts为风电功率采样周期。

由式（6）可知：fc越大，输出功率越接近输入功率；输出功率的曲线越不平滑，滤波效果越差。以fc为循环变量，通过求取各截止频率下的（t）+P0的 ΔP，是否达到风电场有功功率变化的最大限值。当ΔP满足上述要求，停止循环；否则继续加大fc，进而确定低通滤波最优截止频率。

2 基于GRGC的混合储能功率的分配

为避免人为确定混合储能功率的分界点，采用灰色关联度聚类重构高频功率分量，获得能量型、功率型储能介质的功率。本文采用邓氏关联度和 绝 对 关 联 度 来 计 算 各 高 频 分 量Pwre，Pw（wb，3:2n）的几何相似性。关联度越大表示两曲线越接近，反之，两曲线越远离[14]。通过计算各高频分量灰色关联度，聚类重构各子序列，获得能量型和功率型储能的功率曲线。灰色关联度算法步骤如下。

①各分量标准化处理

邓 氏 关 联 度 是 利 用 位 移 差 Δa（t）=|（t）-（t）|反映了两序列间之间的几何相近性，而绝对关联度是按照两时间序列在各对应时段上曲线斜率的接近程度来计算灰色关联度。

邓氏关联度系数：

③计算综合关联度系数

式中：τ为权重系数，取值为0.5。

3 储能充放电功率的SOC模糊优化控制

本文采用模糊控制对功率型以及能量型储能功率进行修正。当功率型储能SOCgl在合适状态时，无需对混合储能功率进行修正。当SOCgl过大或过小，而此时储能下一状态处于充电或放电时，采用模糊理论对其SOCgl进行控制，以当前SOCgl和下一时刻所需SOCgl的变化值 ΔSOCgl作为模糊输入，模糊输出为Pgl的修正系数k，ΔSOCgl计算式为

式 中：tc1，tc2，td1，td2分 别 为 储 能 充、放 电 起 止 时 刻；ηcg，ηdg分 别 为 功 率 型 储 能 充、放 电 效 率；Eglr为 功率型储能的额定容量。能量型储能设备额定容量Enlr的计算过程与功率型储能设备的计算过程相同。

储能的额定容量Eglr由储能的能量变化情况和SOC约束条件求得，即：

式中：SOCup，SOClow分别为功率型储能荷电状态上下限。

模糊输入SOCgl其论域为[0，1]，模糊集为{VS，S，MS，M，B，VB}。模 糊 输 入 ΔSOCgl其 论 域 均为[-1，1]，模 糊 集 为{NB，NM，NS，PS，PM，PB}。模糊控制器的输出量k其论域为[0，1]，模糊集合为{VS，S，MS，MB，B，VB}。SOCgl，ΔSOCgl，k隶 属 函 数及模糊规则、模糊控制器输入输出关系[8]分别如图4，5和表2所示。

表2 模糊控制规则Table2Fuzzy control rules

图4 模糊控制输入、输出的隶属函数Fig.4 Membership function of fuzzy control input and output

图 中VS，S，MS，M，MB，B，VB，NB，NM，NS，PS，PM，PB分 别 代 表 非 常 小、小、中 小、中、中 大、大、非常大、负大、负中、负小、正小、正中、正大。

图5 模糊控制器输入输出关系Fig.5 Input and output relationship of fuzzy controller

修正后功率型和能量型储能功率为

4 仿真分析

本文采用装机容量为60MW的风电站某典型日实际输出功率数据，采样时间为5min，利用Matlab对原始风电数据进行处理，储能系统相关参数如表3所示[7]。

表3 储能系统参数Table3Parameters of the energy storage system

4.1 风电平抑效果分析

由前文可知，选用db6小波作为最优小波基对Pw进行分解，如图6所示。

图6 对风电进行2和3层分解效果及功率波动Fig.6 Effects and power fluctuation of2-layer and3-layer decomposition of wind power

当分解层数n=2时，以10min为时间尺度，计算分离出的P0功率波动 ΔP的最大值超过20 MW，不满足并网要求。当分解层数n=3时，低频分量功率波动最大值为17MW，满足并网要求，最终确定小波包分解层次为3层。

按前文方法确定低通滤波的截止频率，如图7所示。

图7 风电并网功率波动以及最优截止频率下（t）分量的提取Fig.7 Wind power grid-connected power fluctuation and extraction of （t）components at the optimal cut-off frequency

当fc取8×10-4Hz时，风 电 并 网 功 率P10（t）+P0的ΔP最大值为19.3MW，满足并网要求。如图8所示，利用一阶低通滤波算法从高频功率分量Pw（wb，21）中 分 离 出 部 分 可 用 于 并 网 的 风 电 功 率 信息（t），最 终 获 得 的 风 电 并 网 功 率（t）+P0以及并网功率波动。

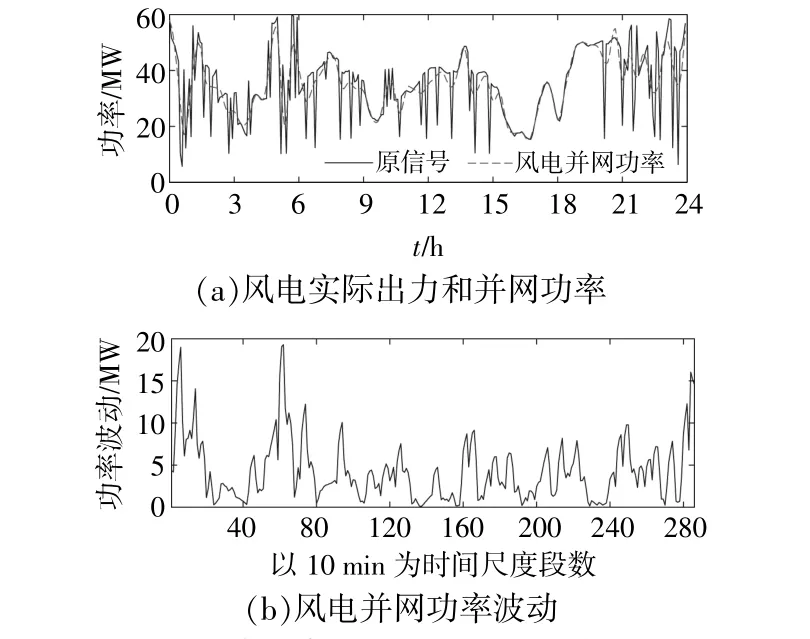
图8 风电平抑效果以及并网功率波动Fig.8 Wind level suppression effect and grid-connected power fluctuation

为验证采用WPD-LPF方法分解风电功率的优越性，分别采用滑动平均法[2]、低通滤波方法[15]、小波包方法[8]和本文方法分解风电功率。计算累计变化功率Psum和以10min为时间尺度的最大变化功率Pmpv，其表达式为

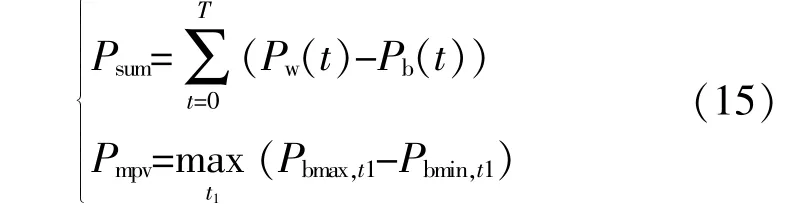
式中：Psum为储能平抑功率，Psum越大对储能系统的容量配置要求越高；Pmpv用于验证各分解算法下Pb是否满足风电并网功率波动标准，即表1中的并网时风电场有功功率变化的最大限值。

将Psum和Pmpv以及储能容量作为评价指标，对比分析如图9所示。各方法下风电平抑效果如表4所示。

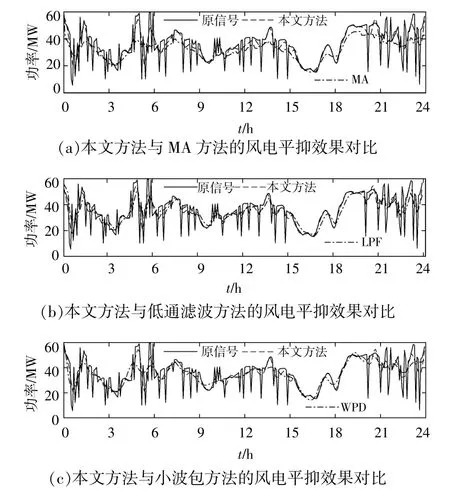
图9 不同控制方法下平抑效果对比Fig.9 Comparison of smoothing results under different control methods

表4分解算法结果对比Table4Comparison results of decomposition methods

由图9可以看出，普通的一阶滤波方法具有明显的延时效应，且无法有效地处理局部突变信号，而本文方法可以实时处理风电数据，显著地平滑风电输出。虽然小波包方法以及滑动平均法下的风电并网功率较本文方法下的风电并网功率更平滑，但分析表4各分解算法结果数据可知，上述4种方法在满足并网波动标准前提下，本文所述方法对储能配置要求最低，蓄电池和超级电容容量分别为28.36，17.32MW·h，证明了该方法能够最大程度获取低频功率分量，进而降低对储能的配置要求。

4.2 SOC模糊优化控制效果分析

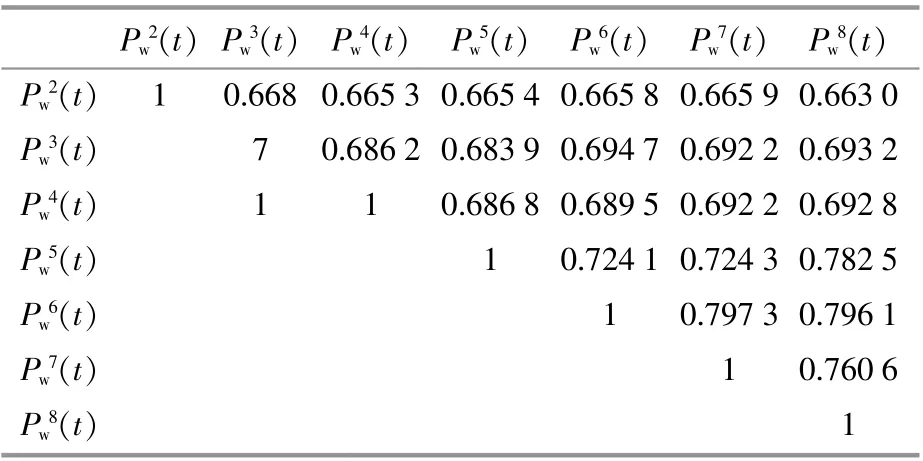
表5 各高频分量之间的综合关联度系数Table5Comprehensive correlation coefficient between each high-frequency component

图10 各高频分量聚类结果Fig.10 Clustering results of each high-frequency component

经SOC模糊优化后的蓄电池和超级电容功率以及荷电状态如图11所示。由图11可知，本文方法可以按照储能介质各自的性能特点分配功率，由蓄电池承担长时间尺度下的功率波动，而超级电容承担短时间尺度下的功率波动。经模糊优化后储能SOC均在安全范围内，未出现越限现象。

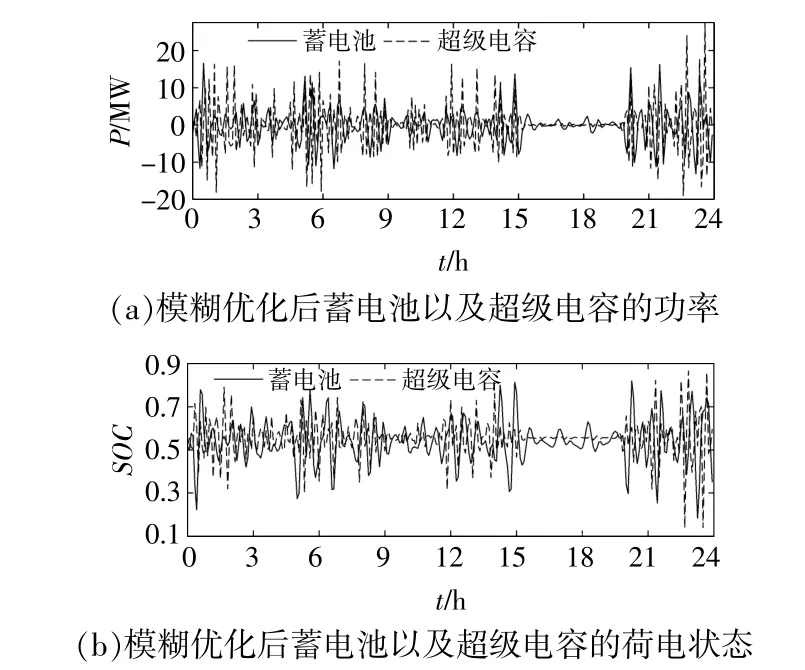
图11 模糊优化后储能功率和荷电状态Fig.11 HESS power and SOC after fuzzy optimization

为了进一步验证SOC模糊优化控制对储能SOC的调节能力，在极端情况将超级电容的初始荷电状态分别设置为30%和80%，对比分析有无模糊优化情况下超级电容的荷电状态如图12所示。

图12 有无模糊优化的超级电容SOCFig.12 Super capacitor SOC with or without fuzzy optimization

由图12可知，无模糊优化控制时，在极端情况下超级电容的SOC容易越限，而加入SOC模糊优化控制可以避免过充过放现象，这证明了SOC模糊优化控制能够保证混合储能系统在极端情况下也能够满足风电平滑需求。

5 结论

本文提出一种利用WPD-LPF和灰色关联度的混合储能平抑风电波动的控制方法。从风电波动平抑效果和储能容量配置需求、SOC模糊优化控制效果分析研究该方法的有效性及优越性，主要结论如下：①利用WPD-LPF和灰色关联度的混合储能平抑风电波动控制策略可实现风电功率的最优分解，大大减小风电并网波动程度，平抑后风电输出功率明显得到改善，且该方法对蓄电池、超级电容的容量需求较传统的利用WPD的混合储能平抑风电波动控制方法的储能需求分别减小6.4%，11.2%，可提升电网对风电的消纳水平，提高储能资源的利用效率；②通过GRGC的混合储能功率初次分配和超级电容SOC模糊修正的储能功率分配策略可实现混合储能内部功率的合理分配，有效避免储能过充过放行为，提高混合储能系统的调节特性和运行经济性。