改进FA优化SVM的风机叶片裂纹检测模型
2022-09-13汤占军孙栋钦李英娜
汤占军,孙栋钦,李英娜,陆 鹏
(1.昆明理工大学 信息工程与自动化学院,云南 昆明 650500;2.云南龙源风力发电有限公司,云南 曲靖655000)
0 引言
能源和环境引发的问题日益增多,世界各国纷纷出台了相应的能源结构转型战略。风力发电得到了广泛的应用,国内风电市场也保持着强劲的增势。叶片是风机的重要组成部分,也是易受损的部件。风沙、雨水、雷击、冰冻,以及在安装过程中的不当操作都会造成风机叶片不同程度的损伤。裂纹类损伤形成后会随着雨水、风沙侵蚀逐渐扩大。此类损伤的早期发现可以给工作人员更多的调整维修时间。裂纹超过一定程度,风力发电机将被迫停机,影响风电场整体的发电计划。更为严重的是,因裂纹过大而导致叶片折断,甚至撞击塔筒。因此,定期检测风机叶片发现早期裂纹是十分必要的。
传统的裂纹人工检测方法主要有3种:地面敲击辨音检测法、地面望远镜观测法、吊车辅助近距离观测法[1]。人工检测方法效率低下,经济、时间成本高。由于受到主观影响,漏检率也比较高。近年来也有人提出对风机叶片裂纹的声发射信号进行模式识别,或是通过分析风机出口气动信号的检测裂纹方法[2],[3]。但一些老款的风力机没有在叶片上安装相应的传感器,不能采集相关的数据。得益于无人机的快速发展,可以利用无人机巡航拍摄风机叶片图像,再将图像传回后台进行人工分析,排查故障,在一定程度上减 轻了巡检人员工作量。无人机巡检机动灵活,且数据存储与传输方便,有利于构建风力行业大数据。但面对无人机巡检拍摄的海量图像,后台工作人员受主观经验影响,难免会出现漏检或误检。借助合适的模型,利用算法对无人机拍摄图像进行裂纹识别有助于克服上述弊端。现有文献对无人机巡检风机叶片图像缺陷检测的相关研究不多。文献[4]通过在鲁棒性主成分分析(RPCA)模型中增加F范数和Laplacian正则项,使模型对缺陷的检测更具鲁棒性。虽然此算法能在一定程度上抑制风机叶片光照不均的问题,但是该算法以超像素为检测单元,对于微小裂纹的检测效果欠佳。
为提高风机叶片微小裂纹的检测效率和准确率,本文提出了利用无人机拍摄的叶片图像结合机器学习的方法进行裂纹识别。利用局部二值模式(LBP)和灰度共生矩阵(GLCM)对图像进行特征提取。用改进的萤火虫算法优化支持向量机(SVM)对特征向量进行训练。为提高算法的搜索能力,引入混沌理论取得更好的种群初始位置,采用自适应步长的萤火虫算法优化SVM参数。
1 图片集处理
为了后续提取图像特征,需要对图片进行预处理。首先将原始图像灰度化,将图像的红、绿、蓝3种颜色按一定的权重转化至0~255的灰度范围内,再进行双边滤波。考虑到像素的邻近关系,也考虑到了亮度上的相似性[5]。裂纹反映在图片上更像是边缘信息。为了更好地保持裂纹信息,双边滤波在灰度值变化大的风机叶片裂纹区域像素范围域权重变大。使用Sobel边缘检测算法是为了使微小的裂纹更加地清晰。图1为图像处理前后的对比图。

图1 图像预处理的对比Fig.1 Comparison of image preprocessing
1.1 LBP特征的提取
LBP算子窗口的大小为3×3,以中心位置为灰 度 阈 值[6]。经 式(1),(2)运 算 得 到 中 心 位 置 的LBP值。将窗口以步长为1移动,待轨迹覆盖整幅图片就得到一幅由LBP值组成的新图。将这幅LBP值图划分为n×n个区域,每个区域都得到一个统计直方图,连接后就成特征向量。
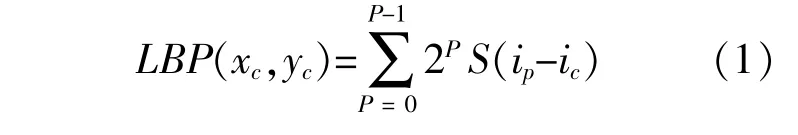
式 中:(xc,yc)为 中 心 位 置 的 坐 标;P为 与 中 心 位置相邻的像素个数;ip为p位置的像素值;ic为中心位置的像素值。
式(1)中 的S(x)为
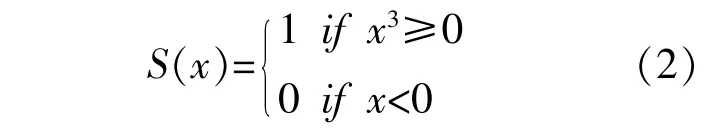
1.2 GLCM纹理提取
GLCM用于分析局部图像,能反映方向、间隔、变化等信息。GLCM是两个像素联合分布的统计概率矩阵,除以矩阵元素的总和,每个元素被归一化为特定距离和角度中对应像素对的概率[7]。
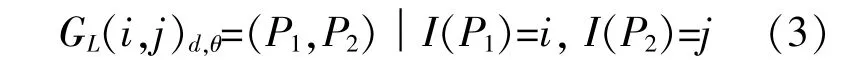
式中:P为像素点;下标d为两像素点的距离;下标θ为方向角;i,j为转换后图像的灰度级。
取以下4个量来组成特征向量。
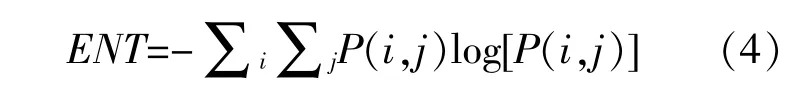
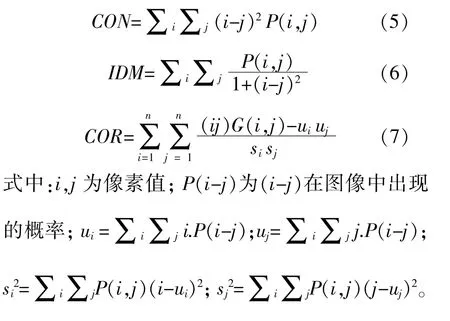
熵ENT反映风机叶片表面裂纹分布的不均匀性或复杂程度,熵值越大,叶片上的裂纹越多越复杂。对比度CON反映纹理清晰程度。裂纹越深像素灰度值差别越大;裂纹越浅灰度值差别越小,对比度越小。IDM为逆方差,风机叶片纹理越清晰、越有规律性、越容易描述,IDM的值越大。相关性COR越大表示在特定方向上灰度值的相关程度越高。图2为提取图片特征向量的基本流程。
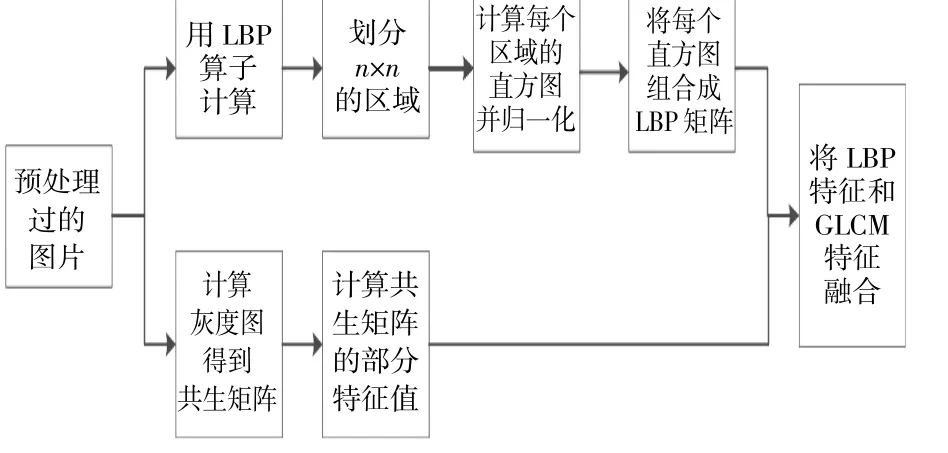
图2 提取特征基本流程Fig.2 The basic process of extracting features
2 SVM分类模型的构建
2.1 SVM介绍
在机器学习中,SVM是与学习算法相关的监督模型,用于分类和回归分析[8]。在样本数量较少且特征向量存在非线性、多维数的情况下,也能有良 好 的 泛 化 能 力。例 如,合 集D=(xi,yi),i=1,2,3…n,xi为 样 本 的 特 征 向 量,yi为 类 别 是+或-,SVM能找到一个将不同类别划分开来的超平面(图3)。
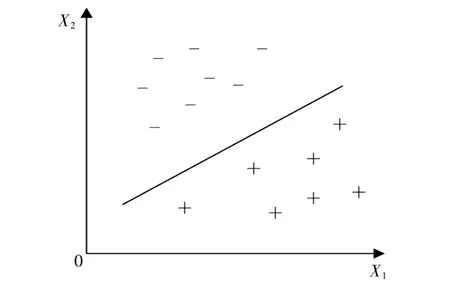
图3 SVM分类基本原理图Fig.3 Basic schematic diagram of SVM classification
由于训练样本的局限性,测试样本可能更加接近划分面。为了让模型有更好的鲁棒性,划分面与两类别的间隔应最大化。在实际应用中常常出现难以确定一个超平面将样本全部分开的情况,当然这样的样本应尽可能少。为此引入惩罚因子c,允许一些样本不满足约束。c越小,受到的约束就越小。现实问题中常常会出现不存在一个超平面能将不同样本分开的情况。为解决此问题,可借助核函数将原始样本空间映射到高纬度特征空间,在高纬度特征空间寻找超平面将样本分类,核函数参数g定义了数据在高维空间的作用范围。
2.2 基本萤火虫算法优化SVM
SVM的分类效果会受到c和g的影响,可以利用优化算法搜索最优解。本文采用改进的萤火虫算法优化SVM的c和g。
采用萤火虫算法寻优c和g,可以看作萤火虫分布在二维平面中,其横坐标x对应c,纵坐标y对应g。在搜索过程中,萤火虫靠光吸引感知范围内的其他个体,同时也受到感知范围内其他萤火虫的吸引,种群向最亮的个体聚集。荧光素值越大,萤火虫发出的光就越亮。初始情况下萤火虫个体的荧光素li和感知半径都相同。搜索过程中荧光素的大小跟萤火虫个体当前所在的位置有关,找到的c,g越适合检测模型,荧光素的值就越大。荧光素的更新公式为
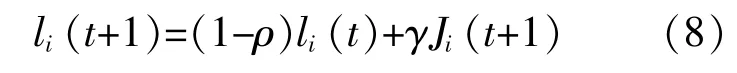
式 中:t为 当 前 的 代 数;ρ(0<ρ<1)为 荧 光 素 的 挥发速率参 数;γ为更 新速 率;Ji(t+1)为t+1代 萤火虫个体对检测模型的适应值。
感知范围随周围个体数量改变。周围个体密度大,感知范围就小,周围个体密度小,感知范围就变大。感知范围更新公式为
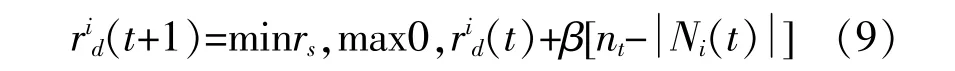
在基本萤火虫算法中,一般采用固定步长寻优,或者采用随着迭代次数增加步长减小的动态步 长d。
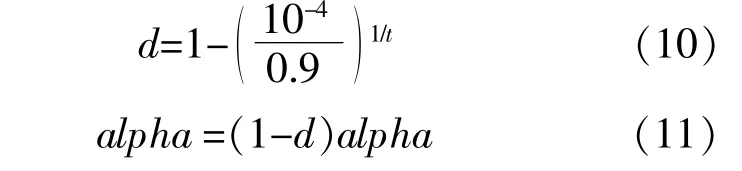
式中:t为当前萤火虫代数;alpha为步长,其初始值 为1。
将萤火虫搜索得到的最优解用作SVM的参数,萤火虫优化SVM的流程如图4所示。
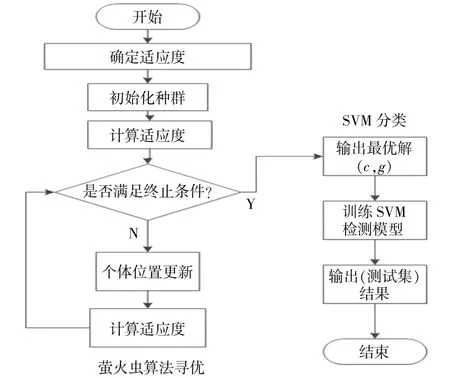
图4 萤火虫优化SVM的流程Fig.4 Flow chart of firefly optimization SVM
2.3 改进萤火虫算法
使用混沌映射随机生成种群初始位置有利于提高初始解的质量。本文引入了logistic映射策略。

式中:μ为混沌系数。
图5为logistic映射图。
由图5可知,在 μ为4时陷入完全混沌。混沌是确定性非线性系统中存在的一种貌似无规则、随机的运动,具有遍历性、随机性和内在规律性[9]。利用混沌的这几个特性,可以在一定程度上防止算法陷入局部最优,提高算法的全局搜索能力,达 到 优 化 的 目 的。根 据 式(13)~(15)生 成 萤 火虫个体的初始位置。
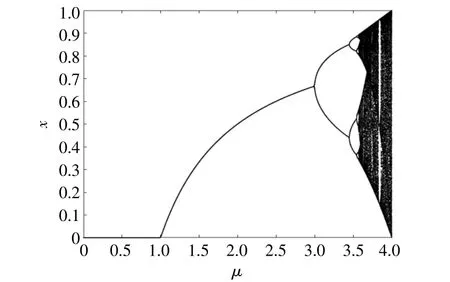
图5 logistic映射图Fig.5 Logistic map
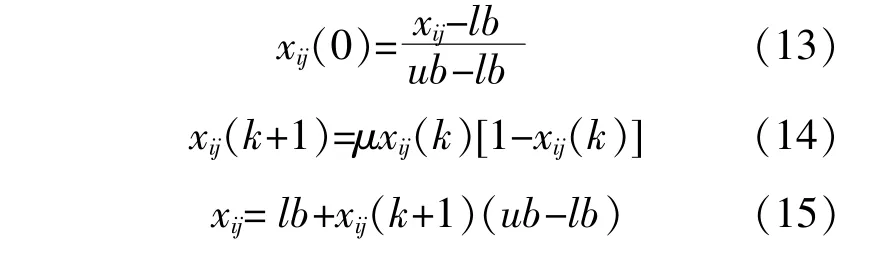
式中:ub,lb分别为xij的上限和下限。
在基本萤火虫算法中,一般采用固定步长寻优。如果步长选择太小会导致算法运行前期个体不能迅速向邻域内亮度高的萤火虫靠近。反之,步长选择太大会导致萤火虫个体无法向最亮的个体进一步靠近。使算法的收敛性不稳定,影响求解精度。针对这种情况,本文采用了文献[10]的自适应步长,引入了荧光因子的概念。
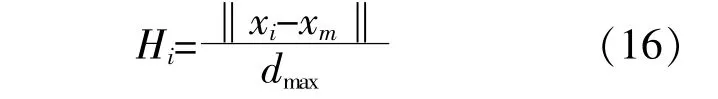
式中:xi为第i只萤火虫的位置;xm为萤火虫中最优位置;dmax为xm到其他萤火虫的最远距离。
按照Hi进行步长的更新。
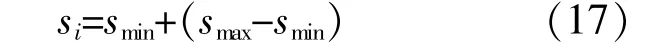
式中:si为步长;smin,smax分别为设定的步长最小值和最大值。
根 据 式(16),(17),随 着 算 法 运 行,萤 火 虫 群中个体的亮度差异减小,移动步长也会相应减小,不至于因步长太大而跳过最优解。
2.4 算法描述
IFA优化分为以下步骤。
①利 用 混 沌 映 射 式(13),(14),(15)生 成 种 群初始位置,设定算法的一系列初始参数,搜索二维空间。
②采用验证集均方根误差作为适应度值。根据式(8)决定荧光素大小,使萤火虫个体在式(9)计算的感知范围内向亮度最大的个体移动,根据式(16),(17)计 算 移 动 步 长。
③每更新一代就重新计算适应度,同时更新荧光素、感知范围和步长,直到最大迭代次数或者达到适应度要求。
④将得到的最优解代入SVM分类器中。
3 实验及结果分析
3.1 风机叶片图片集及处理
本文所使用的图片集来自于云南某风电场的无人机拍摄的风机叶片。86张图片中的叶片带有微小裂纹,282张图片叶片上无裂纹。由于原数据集样本数量不多,容易造成过拟合现象。带有微小裂纹的图像较少,特征向量中可能存在某些部分与无裂纹图像重叠,使得分类器对裂纹的识别度下降。
在无法获得更多新数据的情况下,为减少过拟合的可能,同时解决样本分布不均匀所带来的问题。通过裁剪的方式将大小为400×300像素的原始图像裁剪为300×300像素大小。为保证样本多样性,每一张原图像都经过裁剪,将无裂纹样本扩充到400张,带有微小裂纹的图像经过裁剪后,增 加 旋 转(90°,180°)的 方 式 扩 充,同 样 达 到400张。
将无裂纹、有裂纹两类叶片图片分别记为1和0。随机选取其中480张图片用于模型的训练,160张组成验证集,160张图片用于测试模型的准确度。测试样本的图片不出现在训练集图片库中。
对训练集、验证集和测试集图片预处理,提取图片LBP和GLCM特征并将二者串联,构成每一张图片的特征向量。用改进的萤火虫算法寻优c,g参数后建立SVM风力发电机叶片裂纹检测模型。
3.2 实验结果与对比
改进的萤火虫算法参数设置为n=20,max gen=100,ρ=0.5,l0=5,γ=0.6,r0=10,s0=0.25,smin=0.001,smax=1,β=0.08,nt=5。PSO和GA同 样 设置为n=20,max gen=100。图6为模型的适应度曲线。
由图6可知,IFA收敛曲线下降比GA,PSO,FA都快得多,GA和PSO容易陷入局部最优。由于优化了萤火虫的初始位置,在第一代IFA的求解精度就比FA高。采用了自适应的步长,能够让IFA获得比FA更好的搜索能力,并得到更高的求解精度。
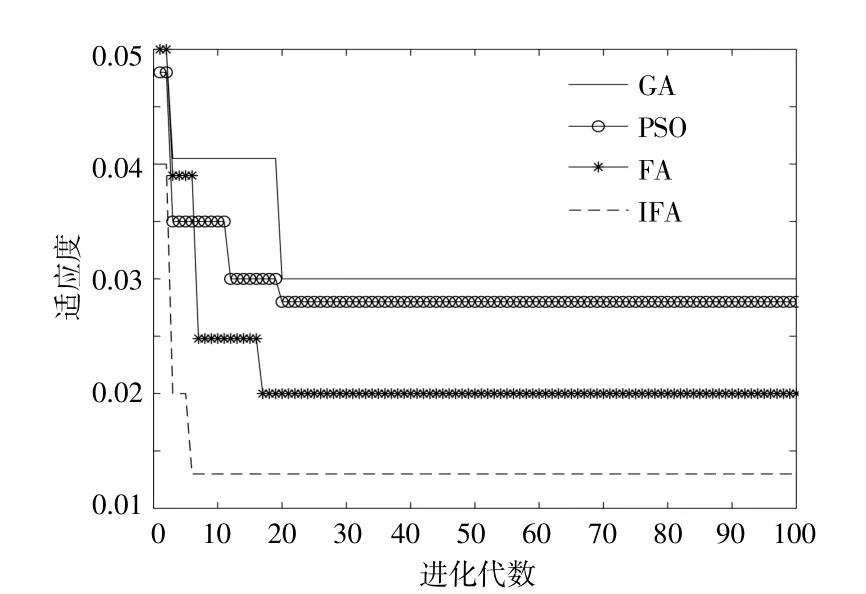
图6 适应度曲线Fig.6 Fitness curve
为检验模型性能,分别用遗传算法优化支持向量机 (GA-SVM)、粒子群优化支持向量机(PSO-SVM)、萤火虫算法优化支持向量机(FASVM)和IFA-SVM检测。用所有图片集做实验后,再用600张背景复杂的图像(风机建造在山顶,叶片背景中常常出现树木和云层)分训练集、验证集和测试集进行30次独立实验。记录结果进行比较,主 要 衡 量 指 标 是 准 确 率(Accuracy,A),查 准 率(Precision,P)和 查 全 率(Recall,R):

表1,2分别为各种检测模型的性能比较和复杂背景下各种检测模型的性能比较结果。
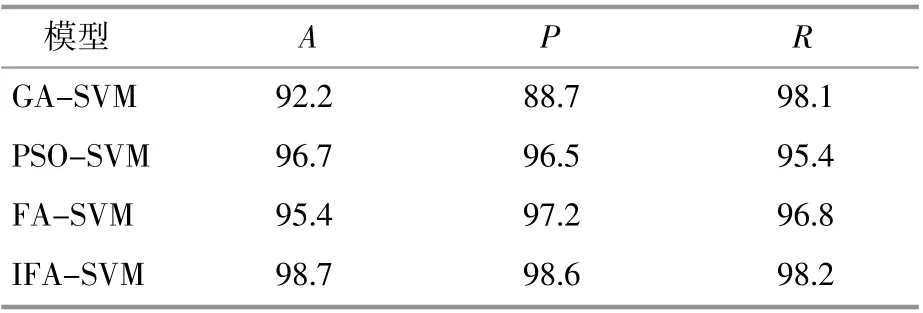
表1 各种检测模型的性能比较Table1Performance comparison of various algorithms %
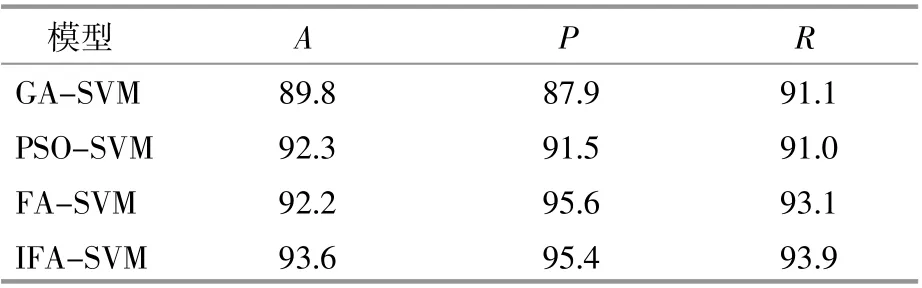
表2 各种检测模型的性能比较(复杂背景)Table2Performance comparison of various algorithms(complex background)%
由表1,2可知,背景越复杂识别效果就越差。本文算法在两种情况下比GA-SVM,PSO-SVM,FA-SVM都表现出更好的性能。由于将有裂纹的叶片误查成无裂纹的叶片可能引起严重的后果,查准率显得尤为重要。在查准率上本文算法对比其他算法均有不同程度的提高,说明了本文方法的有效性。
4 结论
为提高风机叶片微小裂纹的检测效率和准确率,本文提出一种利用无人机拍摄的叶片图像结合机器学习进行裂纹检测的模型。提取图像纹理特征,用改进的萤火虫算法优化的SVM模型进行识别,得到以下结论。
①通过对图像进行预处理能有效地减少模糊,提高提取的纹理特征质量。
②改进的萤火虫算法优化的SVM模型与GA-SVM,PSO-SVM和FA-SVM进行对比,SVM模型获得了更高的准确率、查准率和查全率。
