基于Grubbs准则和直线线性度拟合的线纹提取算法

沈良辰， 郭钢祥， 孔 明， 郭 斌

(1. 中国计量大学计量测试工程学院，浙江 杭州 310018; 2. 浙江省计量科学研究院 长度与精密测量研究所，浙江 杭州 310018)

0 引 言

钢卷尺作为常用的测量工具，其检定精度是检定过程中的重要参数。目前主流的自动检定过程普遍基于机器视觉的技术：赵保亚提出基于边缘检测的钢卷尺图像二值化方法[1]，该方法提出基于同态滤波和改进的Sobel算子进行线纹边缘检测，从而实现对线纹刻线的提取[1]；景加慧提出边缘检测特征值提取算法结合分段最小二乘拟合，实现刻线的提取[2]；苟建松提出了图像阈值分割

并结合垂直投影定位算法来提取线纹刻线[3]；Menaka在现场可编程门阵列（FPGA）板上基于Sobel滤波器设计了一种边缘检测算法[4]，实现了刻线特征提取和模式识别。上述方法使用了图像处理里的边缘检测、阈值分割以及最小二乘拟合等理论，对线纹图像处理并提取刻线、比对刻线，过程高度自动化，因此大大降低了劳动力，提高了效率，同时用机器视觉取代了人眼，也极大地提高了检测精度。

但是目前自动检定方法存在的问题是：图像处理过程中会损失大量线纹边缘处的信息，而且由于线纹边缘并非均匀分布，可能存在缺口、凸起等凹凸不平的情况，导致得到的线纹边缘特征点位置信息不准确，甚至有较大偏差[5]，这就带来了含有粗大误差的特征点，也叫作奇异点，影响后续线纹边缘线拟合的精度。同时采用的直线拟合方法也较为落后，拟合的线纹中心线线性度不高，而直线线性度不高则会直接影响后续线纹比对的精度，从而极大地降低检定精度。

因此，提取到更加精确且直线度高的线纹进行比对，成为影响检定精度的重要因素。本文在吸收自动检定方法优点的基础上，提出了基于Grubbs准则和直线线性度拟合的线纹提取算法。首先，线纹刻线提取过程改变提取线纹刻线边缘特征点这一做法，而是采用根据线纹截面灰度值特征分布的特点来定位线纹中心特征点，极大程度上降低了因为提取刻线边缘而造成有效信息的损失的情况；得到较为准确的线纹中心特征点后，采用基于Grubbs准则和直线线性度的拟合算法，去除了因边缘误差而引入粗大误差的奇异点的同时还能拟合出线性度高的直线。

本文提出了一种线纹检定的新方法，且经过实验验证这种方法与现有的自动检定方法相比，检定精度更高，有着较大的实际应用价值。

1 线纹中心特征点的定位

线纹中心点的定位是拟合算法的重要前提。本章从线纹截面灰度值特征分布的特点出发，得到线纹灰度直方图，并对其平滑，寻找平滑后图像灰度值锐减和锐增的两个阶跃点，进而精确定位线纹中心点。

1.1 线纹截面灰度值特征分布

在理想条件下，线纹截面（即图1中红线沿着白色箭头方向）单列像素行的灰度直方图函数接近矩形窗函数[6]。

图1 提取单列像素列像素灰度值

矩形窗函数的数学定义式为：

即在某个特定区间内函数值为1，其余区间函数值为0，M-1为矩形窗的长度。

理想情况下线纹截面灰度值特征分布也与之类似。黑色线纹区域的灰度值为0，而非线纹区域的灰度值为[0,255]区间内的任一数值，其具体数值与不同钢卷尺的背景底色有关。因此，定义理想情况下线纹截面单列像素行的灰度值直方图函数为：

由于实际钢卷尺制造印刷水平不一、钢卷尺线纹磨损情况不同等因素导致线纹区域并非为灰度值为0的纯黑，其灰度直方图函数曲线也并非像矩形窗函数那样非0即1，而是存在一定的数值波动，但是总体曲线形状仍与窗函数类似，即在非线纹区域灰度值较高，接近线纹边缘区域灰度值急剧下降或上升，线纹区域内灰度值较低，与非线纹区域灰度值存在明显的高度差。

为了得到线纹截面灰度值特征分布进行分析，提取待测线纹任一像素列的各个像素点的灰度值，即图1中红色像素线区域（红色像素线宽度为一个像素），形成单列像素行像素灰度直方图，如图2所示。

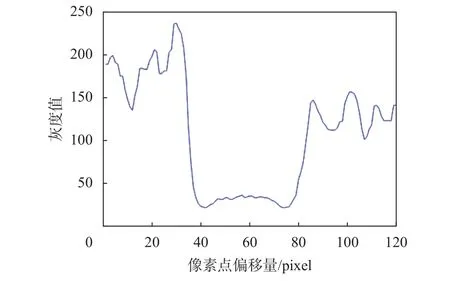
图2 单列像素行像素灰度直方图

从图像中可看出，曲线满足上文描述的“窗函数”的性质。

1.2 单条线纹中心点的定位

由于提取到的单列像素灰度值形成的灰度直方图毛刺较多，也存在着高频噪音，不利于后续确定中心点，因此需要进行平滑处理。针对图像的特点，采用Savitsky-Golay平滑算法。

Savitsky-Golay平滑算法的原理是通过多项式对移动窗口内 N =2r+1的数据进行多项式最小二乘拟合，算出窗口内中心点关于其周围点的加权平均和[7-8]，从而完成平滑处理。Savitsky-Golay平滑后原图像及其局部放大图像如图3(a)、(b)所示。

图3 Savitsky-Golay平滑后图像

Savitsky-Golay平滑后的曲线，需要找到灰度值锐减和锐增的两个阶跃点，这两点即位于线纹的上下边缘。IndMin函数可以自动遍历曲线并获取曲线上所有极小值点，因此通过调用IndMin函数获取曲线上所有极小值点，即可得到所求的阶跃值点及其横坐标值。IndMin函数获取曲线极小值点示意图如图4所示，横坐标值40附近的极小值点与75附近的极小值点为所求的两个阶跃值点。因为像素灰度值在线纹内部是均匀分布的，因此对这两点横坐标进行1∶1加权取中值便可定位线纹中心点。

图4 IndMin函数获取曲线极小值点示意图

可定位一个位于中心线上的特征点。将上述单像素列水平平移一个像素的距离，便可得到一个新的像素列，对此新像素列继续定位中心特征点。以此方法水平移动像素列，使之遍历整条线纹，便可得到大量中心特征点。为了方便实验，本文将单条刻线水平等间距分成20等分，即只取20个离散点当做拟合直线原始点（实际上，经验证，当取20个点拟合出来的直线精度已很高），如图5所示。

图5 单根刻线上按灰度值取出的20个离散点

2 基于Grubbs准则和直线线性度的拟合算法

对数据点拟合一般运用最小二乘法。但如上文所述，由于线纹边缘并非均匀分布，可能存在缺口、凸起等凹凸不平的情况，这就带来了含有粗大误差的特征点，也叫作奇异点，影响后续线纹边缘线拟合的精度；而且最小二乘法对数据点中的“极佳直线”没有辨别的能力。其中，极佳直线是所有拟合直线中效果最好的一条，即要满足直线的线性度高且参与拟合该直线的点数目最多的要求。所以，运用最小二乘法无法排除奇异值点的干扰，并拟合最优直线[9]。这样的拟合结果显然无法满足高精度线纹中心线的要求。针对最小二乘法存在的不足之处，提出了一种基于Grubbs准则和直线线性度的拟合算法，去除了含有粗大误差的奇异点的同时还能拟合出线性度高的直线。

2.1 Grubbs准则

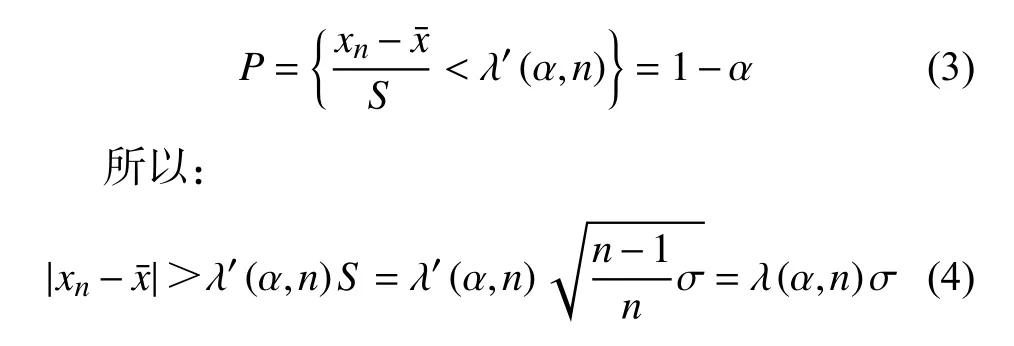
2.2 拟合算法原理

首先定义一系列变量：

图6 点与拟合直线示意图

3）剔除距拟合直线最远的点数目J。根据经验设定最优直线线性度以及L和J的值。假定为需要拟合的离散数据点集，，，，，，，Q(max)，为在程序运行中用来存储的相应点集。

基于Grubbs准则和直线线性度的改进拟合算法具体实施程序流程图7所示。

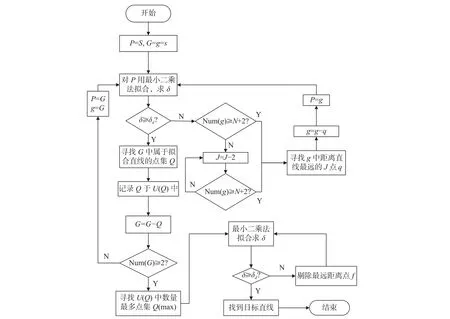
图7 基于Grubbs准则和直线线性度的改进拟合算法程序流程图

基于Grubbs准则和直线线性度的改进拟合算法的原理是：先以为准则，结合L和 J的值，多次利用最小二乘法并结合Grubbs准则，将线纹中心线上的数据点粗分成若干个数据点集，每一个点集中的点与相应拟合直线的距离都在L范围内，即这些点属于相应直线，距离在L范围外的点视为奇异点不参与拟合计算过程；然后寻找到上述若干点集中含有离散数据点数量最多的点集，此点集即为包含线纹中心线的点集; 接着再次以为准则，将含有离散数据点数量最多的点集利用最小二乘法循环拟合，直到拟合的直线线性度不小于为止，即得到所求的线纹中心线。

2.3 线纹提取

当一条中心线确立后，可以按照同样的方法确立其余线纹的中心线，但是产生了一个问题：理论情况下，钢卷尺上各条线纹都是互相平行的，也就是说，不同线纹的中心线也是相互平行的。然而，按照上述算法，不同线纹拟合出的中心线的直线方程各不相同，进而斜率也不相同，这样拟合出来的中心线也不符合实际，而且这也给计算两条中心线纹之间的距离带来了困难。

为了解决这一问题，引入定斜率直线拟合的方法。因为各条线纹图像是平行的，因此按照上述算法拟合出来的各条线纹中心线的斜率虽然不一样，但是两者之差极其微小，可以忽略不计。另一方面，根据数学中的近似相等原理[11]，当两条直线斜率相同且这个斜率数值非常接近于零时，这两条直线之间的距离即为两条直线方程截距之差的绝对值[12]。如图8所示，当趋向于0时，设为两条直线方程式中的截距差，为两条直线的垂直距离，则。

图8 水平距离与截距差关系示意图

根据上述原理，线纹提取过程的步骤为：首先选定一根样貌较为完整、形态较为良好的的刻线作为标准刻线，定位线纹中心特征点，然后使用2.2中的算法进行直线拟合并得到直线方程，设为y=kx+b；然后以该方程的斜率为标准量，按照2.2中的算法去拟合其余的直线，即其余直线可表示为 y =kx+m1、 y =kx+m2···其中、为待求参数；得到各线纹中心线与此标准线纹中心线的截距差，即两条直线间的距离再将此距离（像素值）转化成长度值，与高精度测量设备如影像测量仪测得的各线纹间距数值做对比，即可得到示值误差；最后进行误差评定，验证算法的效果。

3 实验及误差评定

本实验采用1 000万像素的工业相机拍摄局部线纹区域，拍摄的得到的原始线纹图像为分辨率3 840×2 748的灰度图，用作比对的标准设备为SEREIN公司型号为SVM 3 020 DCC Classic的影像测量仪，实物如图9所示，其准确度0.05 μm。

图9 SEREIN影像测量仪实物图

按照上述方法，以钢卷尺1 m附近的一根刻线为标准，分别对距离其1 mm、2 mm、3 mm、5 mm、10 mm的刻线进行中心线的提取，计算这些中心线距离标准中心线的实际距离，并与影像测量仪对其测量的结果进行比对，得到示值误差值。同理，使用对比算法进行重复实验，即使用引言中景加慧提出的边缘检测图像处理的自动钢卷尺检定方法对上述五条刻线进行刻线提取并与影像测量仪测得的标准值进行比对，得到示值误差值，并对两种方法的测量结果进行分析。

首先选定一根样貌较为完整、形态较为良好的的刻线作为标准刻线，按照上述实验方法，可得到最终拟合出的直线方程为：

图10 标准线纹中心线拟合结果图

以此标准直线方程，对距其1 mm、2 mm、3 mm、5 mm、10 mm的刻线进行中心线拟合，设直线方程为：

其中 n =1,2,3,5,10。 |mn-667.507|即为各中心线与标准中心线之间的像素距离，最后根据换算关系（1像素等于5.58 μm）将像素值转化为长度值即可得到最终距离。使用边缘检测算法的检定结果如图11所示，使用本文算法的检定结果如图12所示，影像测量仪检定结果如图13所示。

图11 边缘检测算法检定结果

图13 影像测量仪检定结果图

两种线纹检定结果与影像测量仪检定结果的对比及示值误差值如表1所示。对测量结果分析可得，采用本文算法对钢卷尺进行检定的示值误差已远远小于JJG 4—2015 《钢卷尺检定规程》中所规定的Ⅰ 级钢卷尺±0.1 mm的标准[13]，与基于边缘检测算法的检定方法相比，示值误差也大大降低。

表1 本文算法结果与影像测量仪测量结果对比表

4 结束语

本文提出了基于Grubbs准则和直线线性度的拟合算法进行线纹检定，采用根据线纹截面灰度值特征分布的特点来定位线纹中心特征点，极大程度上降低了因为提取刻线边缘而造成有效信息的损失的情况；得到较为准确的线纹中心特征点后，采用基于Grubbs准则和直线线性度的拟合算法，去除了含有粗大误差的奇异点的同时还能拟合出线性度高的直线。具有较为实际的现实应用价值。