TRP测量中球面采样方法研究

李淑颖， 周远国， 武风波

(西安科技大学通信与信息工程学院，陕西 西安 710054)

0 引 言

国际标准化组织3GPP（3rdGeneration Partnership Project）定义 5G NR（new radio）的两个工作频段：FR1（410～7 125 MHz）频段和 FR2（24.25～52.6 GHz）频段，其中FR2频段即5G毫米波频段，在5G毫米波频段，天线阵列与整机一体化设计，采用高度集成化架构，天线与整机难以拆分，其射频指标测试需要采用全OTA（over the air）的方式实现，传统的传导测试方式不再适用，其中针对辐射杂散类指标，要求以总辐射功率即 TRP（total radiation power）的方式进行测量。与传统的天线方向性系数测量方法类似，TRP测量需要在OTA球面全空间完成采样，需要综合考虑测试效率和测试精度的问题，在测试方法上存在一定的特殊性。

在国外，以标准组织和设备厂商为主导，针对TRP的测量方法已有一些前瞻性的研究[1-2]，其很早便识别到传统的TRP测量方法在工程实现过程中的缺陷，使用OTA球面全空间采样的方式所需的采样点数量庞大，造成测试难度大且测试效率低，文献[3]中针对如何提升TRP测量效率做了开创性的研究，证明参考栅格采样法的可行性，文献[4]基于参考栅格采样法，提出“改进型的球面等栅格法”和“广义螺旋线法”，均在一定程度上减少了采样点数，采样点规模降低25%，测量精度差异小于0.1 dB，但是却没有结合测量对象的特征做进一步深入研究，所以测量效率的提升效果并不明显。

在国内，近年来，学术界针对5G毫米波OTA测试的若干关键问题开展了大量的探索性研究，主要集中在如何低成本高效率的实现EIRP （equivalent isotropically radiated power）类射频指标的测量[3]，在测试能力维度上详细对比分析了不同暗室间的差异，而对TRP类射频指标的测量方法研究内容极少。

结合国内外研究现状调研，针对前文提及的TRP测试效率和测试精度的问题，本文主要讨论了如何在误差允许范围内减少采样点数，提出基于待测件方向图特征的球面采样方法，经过充分的算法仿真验证，证明本文中所阐述的TRP测量方法可以在确保测量精度的前提下，提高测量效率，降低测试系统的复杂度。

1 球面等栅格采样法

TRP定义为远场EIRP在球面上的积分，如图1所示，理论上需要连续获取球面上每一点的EIRP值，才能准确计算TRPreference，如下式所示[4-5]：

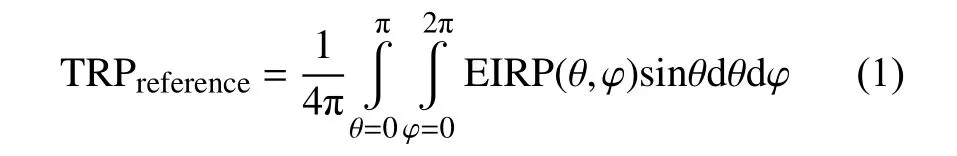
图1 球面坐标系

一般情况下，通过球面离散数值积分的方法来近似估算TRPestimate，如式（2）所示，把整个球面按照一定的栅格大小离散化，在θ和φ方向上分别划分为N和M个等距子区间，栅格大小Δθ和Δφ如式（3）所示，当N和M趋于无限大时，TRPestimate无限接近TRPreference，此时在实际测量可以获取最高的测量精度。

假设待测阵列的长宽高分别为d，w，h，其中DS表示包围待测阵列的最小球体的直径，DC表示包围待测阵列的最小柱体直径，那么DS和DC可以表示为式（4），定义θ和φ方向上的参考栅格大小分别为Δθref和Δφref，针对不同的频点，参考栅格大小如式（5）所示，参考栅格大小的上限为15°，这确保了，当波长远大于待测阵列尺寸时的测量精度[6]。

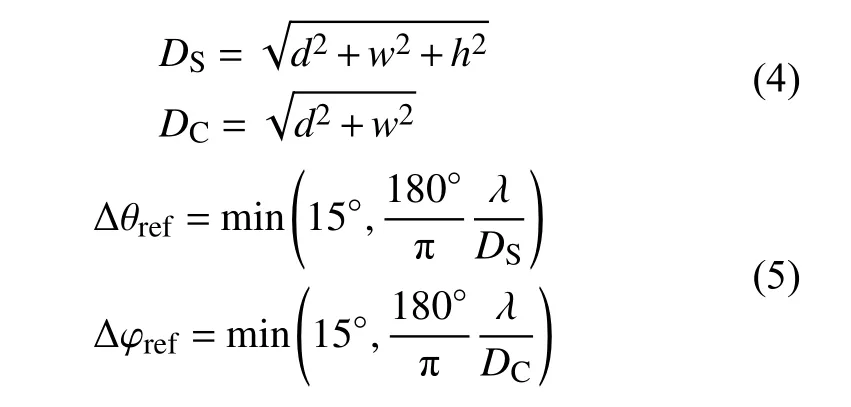
TRP测量存在多种不同的球面离散方法，不同的球面离散方法在测试精度和测试效率上存在较大的差异，球面等栅格采样作为一种通用的球面离散方法，适用于所有的TRP测量需求，在实际应用中可以提供最高精度的测量结果，下面将介绍，对于不同的信号类型，如何在确保测量精度的前提下，进一步提高测量效率。

2 基于方向图相乘的正交切面采样法

针对带内互调信号，如邻道泄露功率比（ACLR）和带内无用杂散（OBUE），其特征是与主信号具有较强的相关性，在天线阵列已知的前提下，此类信号的方向图更接近于主信号的方向图，针对此类信号的TRP测量需求，一般采用正交切采样法，如图2所示，利用正交切面数据来估算TRPestimate，一个切面是经过波束峰值点的水平切面，另一个切面是经过波束峰值点的垂直切面，水平和垂直切面的EIRPav及 TRPestimate如式（6）和（7）所示。正交切面需要已知波束的最大指向，任何角度的偏差都有可能降低测量精度[7-8]。

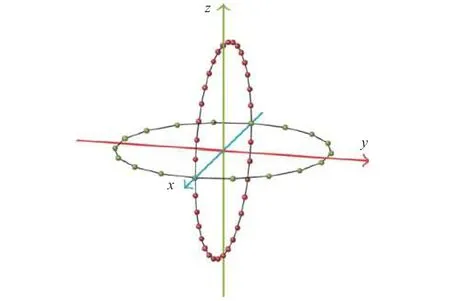
图2 正交切面采样

为了进一步提高测量精度，基于正交切面采样法，当主信号波束指向阵列的法线方向时，方向图具备很好的空间对称性，可基于方向图相乘原理，利用两个正交切面的数据估算全空间信息，方向图相乘原理定义在UV坐标系下，球面坐标系与UV坐标系的变换关系如下式所示：

如图3所示，EIRPcut1(u)和EIRPcut2(v)分别表示两个切面，以EIRP最大点做归一，归一化后，EIRP最大点为0 dB。通过方向图相乘可以将两个正交切面的数据扩展到全空间，如式（9）所示。基于方向图相乘的正交切面采样法估算TRPestimate可以表示为式（10）。

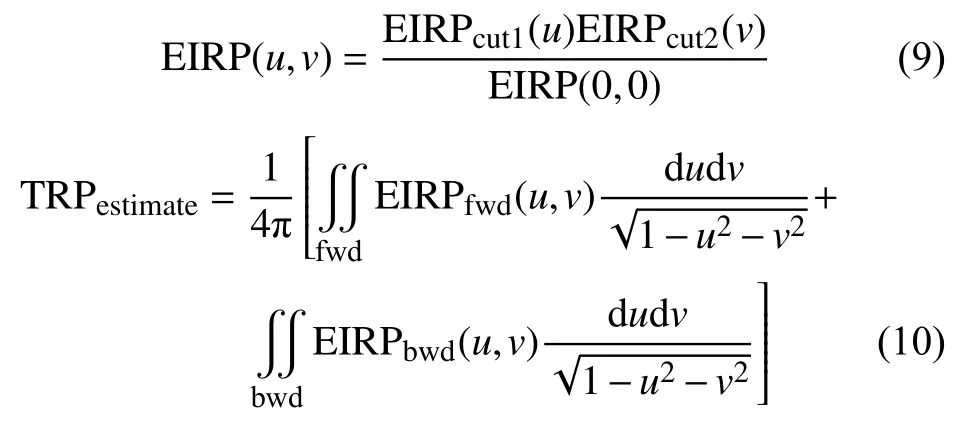
图3 基于方向图相乘的正交切面采样

假设Δθref=Δφref=15°，按照球面等栅格采样法，整个球面需要完成264个样点的测量，但是按照正交切面法，整个球面只需要完成46个样点的测量，效率提升接近80%。

3 基于稀疏算法的球面等密度采样法

针对带外杂散信号，无法预估其方向图特征，根据当前3GPP通信协议的要求，毫米波频段的TRP杂散测量频率要求从30 MHz～60 GHz，相比于传导测量，如果在全频段范围内使用球面等栅格法测量TRP，测量时间会成百倍的增加。针对这个问题，可以借鉴EMC的测量方法[9-10]，先使用预扫描法，识别可能存在较高辐射杂散的“可疑频率区间”，再对这些频率区间做进一步的精细测量，但有可能存在多个“可疑频率区间”，导致后续精细评估效率依然过低[11-12]。

为了进一步提升测量效率，针对这些“可疑频率区间”，在球面等栅格法的基础上，提出基于稀疏算法的球面等密度法，所谓“稀疏”，就是将整个球面稀疏划分为等面积的N个子区间，如图4所示，为一个单位球体(半径为1个单位)的球面等密度划分的示意图，球面等面积划分的方法有很多种，这里就不再赘述。

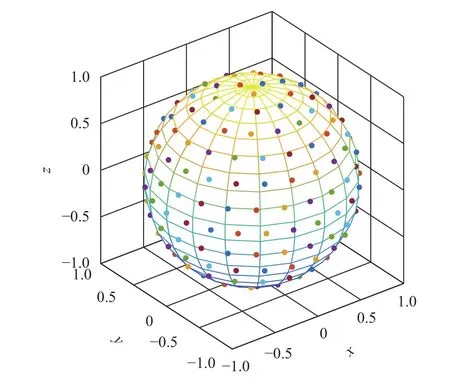
图4 球面等密度采样

测量每个子区间中心位置的辐射功率，记为EIRP(θn,φn)，则 TRPestimate可以表示为式（11），总采样点个数N可以参考等栅格法，按照式（12）来确认。

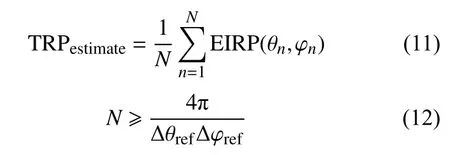
假设Δθref=Δφref=15°，按照球面等栅格采样法，整个球面需要完成264个样点的测量，但是按照球面等密度法，整个球面只需要完成184个样点的测量，效率提升接近30%。

4 不同采样方法测量精度与效率对比

为了验证测试算法的精度及效率，利用一个二元线阵来模拟阵列天线，如图5所示，一个位于位于YZ平面的喇叭天线二元线阵，阵列大小d=3.4λ，w=1.5λ，h=4.2λ，根据式（4）和式（5），可以计算Δθref和Δφref，即Δθref=10°，Δφref=15°，为了便于对比分析，精细栅格大小选择Δθacc=1°，Δφacc=1°。假设阵列输入总功率为1W，则TRPreference为30 dBm。分别使用球面等栅格采样法，正交切面采样法，基于方向图相乘的正交切面采样法及球面等密度采样法，依据阵列方向图的特点做采样分析，结果如表1所示[13]。

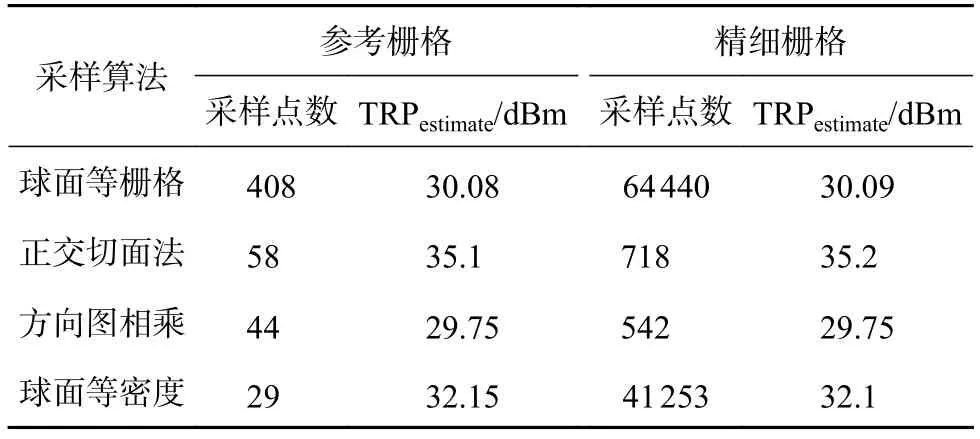
表1 采样算法测量精度与效率分析

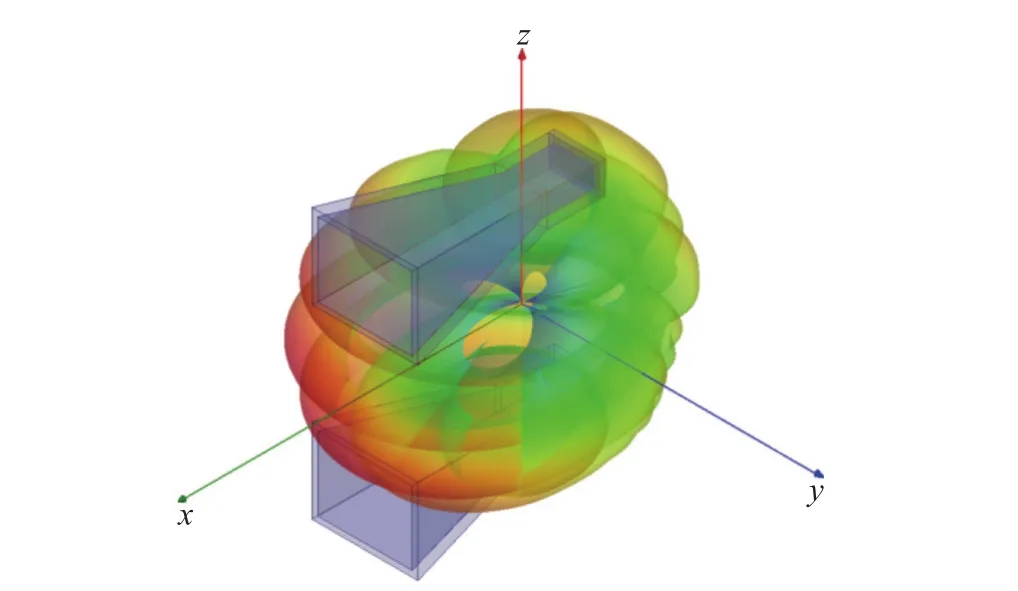
图5 喇叭天线二元线阵

从表格数据分析，可以得到如下结论：

1）同一种采样方法，基于参考栅格Δθref和Δφref所得TRP与基于精细栅格Δθacc和Δφacc所得TRP，测量精度相当，差异小于0.1 dB，但是在测量效率均带来了90%以上的收益，因此参考栅格法具备高精度高效率的特点。

2）不同的采样方法中，从测量精度角度分析，球面等栅格法精度最高（Δa=0.08 dB），其次为方向图相乘法（Δb=0.25 dB），第三为球面等密度法（Δc=2.15 dB），最后是正交切面法（Δd=5.1 dB）；从测量效率角度分析，球面等密度法效率最高，其次为方向图相乘法，第三为正交切面法，最后是球面等栅格法。

3）在参考栅格条件下的方向图分布如图6所示，基于方向图相乘法和基于球面密度法的拟合方向图与理论仿真基本一致，如图7所示，综合测量精度及测量效率，方向图相乘法和球面等密度法整体性能表现最优。

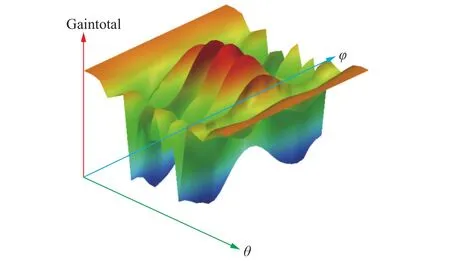
图6 参考栅格条件下方向图分布

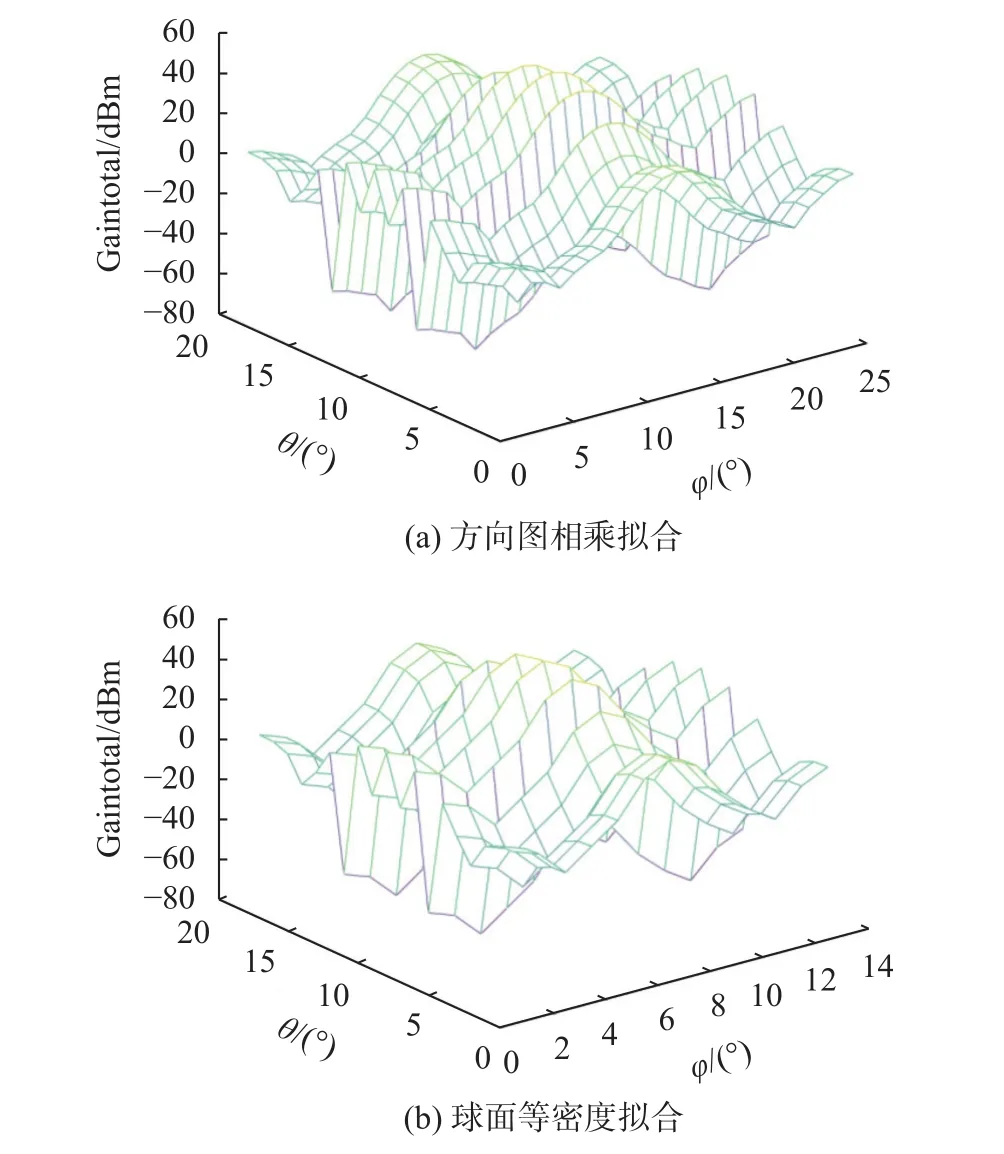
图7 基于采样点拟合方向图分布

5 结束语

本文聚焦于TRP测量中球面采样算法的分析，在测量效率和测量精度之间权衡优化，首先从分析待测件方向图特征出发，对于主信号和带内互调信号的TRP测量需求，提出基于方向图相乘的正交切面采样法，利用方向图相乘原理估算全空间信息，从而计算TRP，而对于带外杂散信号的TRP测量需求，提出基于稀疏算法的球面等密度采样法，将整个球面稀疏等密度划分，通过N个等面积子区间的数据来估算全空间信息，从而计算TRP。经过充分的算法仿真验证，这两种方法均有效确保了测量精度，且较大提升了测量效率，可广泛应用于TRP测量中。