钢井架斜撑柱计算长度系数求解方法探讨
2022-09-13陈威克中国恩菲工程技术有限公司北京100038
陈威克(中国恩菲工程技术有限公司,北京 100038)
1 前言
钢井架是生产矿井地表最重要的构筑物之一,它的用途是通过天轮和钢丝绳,支持地表提升机从事各种提升工作。 在生产期间,钢井架用于井下矿石的提升,人员上下和材料设备的输送。 在凿井期间,钢井架还可用于支承各种掘进设备。 钢井架相较于钢筋混凝土井塔具有强度高,自重轻,抗震性能好,加工制作方便,施工安装周期短等优点,在矿山工程领域有着广泛的使用。 近年来随着矿山生产规模的扩大,多绳摩擦式提升机作为提升系统的重要设备也呈现了大型化的趋势,钢井架承受的荷载也随之变大。 钢构件相对于混凝土构件要细长和薄弱,容易发生失稳现象。 斜撑柱是钢井架的主要受力构件,斜撑柱的稳定是钢井架设计中应予以重视的问题。
2 钢井架分析与稳定设计方法简述
目前,钢井架设计可依据国家标准GB50017—2017《钢结构设计标准》(以下简称《新钢标》)和GB50385—2018《矿井井架设计标准》(以下简称《井架标准》)。
《新钢标》将钢结构分析与稳定性设计方法分为:一阶弹性分析法、二阶P-Delta 弹性分析法以及直接分析法。 一阶弹性分析法针对的对象是不考虑结构整体几何缺陷和构件初始几何缺陷的结构模型,该方法首先对不考虑缺陷的而且未发生变形结构模型进行内力和位移计算,然后进入构件设计阶段,在构件设计时通过计算长度系数反应结构和构件的初始缺陷。 一阶弹性分析法,允许内力和位移的线性叠加,这一规定为设计工作提供了很多便利。与一阶弹性分析法不同,二阶弹性分析法针对的分析对象是考虑结构初始几何缺陷的结构模型,直接分析法针对的分析对象是同时考虑结构初始几何缺陷和构件初始几何缺陷的结构模型,这两种方法不允许荷载和位移的线性叠加,需要进行非线性分析,在构件设计阶段不再考虑计算长度系数。
一阶弹性分析法是设计人员比较熟悉的一种方法,目前在实际的设计工作中仍得到广泛的使用,计算长度系数是该方法的关键参数。 晚于《新钢标》颁布的《井架标准》中规定:非本行架式斜撑柱(以下简称斜撑柱)计算长度系数应根据梁柱刚度比计算,平面内计算长度系数可取1.5 ~1.8;平面外计算长度系数可取1.1 ~1.3,但并未给出具体的计算公式或计算案例,也未在正文中提及其他设计方法,如果再设计中均取上限值可能会造成材料浪费。 《新钢标》中给出了梁柱垂直的规则框架根据梁柱线刚度比求计算长度系数的公式和数据表格,JGJ99—2015《高层民用建筑钢结构技术规程》也给出了类似的公式。 钢井架的斜撑柱构件与各层横梁的夹角不垂直,因此不能运用上述公式。 现阶段《井架标准》和《新钢标》中对构件计算长度的规定,在井架斜撑柱的设计工作中直接应用还存在困难。
3 利用屈曲分析求计算长度系数
钢井架是一种典型的空间结构,各构件的端部约束条件复杂。 钢井架斜撑柱计算长度的求解,属于复杂边界条件下的杆件计算长度求解问题。 在民用工程领域,多采用线性屈曲分析解决类似问题[1-3]。 钢井架设计的有关文献中,关于这种方法的介绍较少,以下将对这种方法的原理和求解步骤进行简要介绍。
3.1 欧拉公式和屈曲分析
材料力学规定,对于各种杆端约束情况,中心受压等直杆临界力的欧拉公式[4]可写成统一的形式为

式中,Pcr为失稳临界荷载;EI是杆件弹性模量和惯性矩;l0是杆件几何长度;μ是杆件的计算长度系数。将式(1)进行变形,可以求得计算长度系数μ的一般计算公式为

显然,求解失稳临界荷载Pcr,是获得计算长度系数μ的关键步骤。Pcr是作用在杆端的外力,可通过屈曲分析得到的杆端轴力(内力)求解[5]。
对某个结构模型而言,在一定的变形状态下的结构杆件的静力平衡方程可以写为

式中,KE为杆件的弹性刚度矩阵;KG为杆件的初始几何刚度矩阵;{u}为杆件的节点位移;W为杆件的外力向量;kg表示标准单元几何刚度矩阵;P表示杆件的初始轴力。 如果杆件承受的外力没有变化,而位移趋于无限大,表明杆件发生屈曲(失稳)。 通过式(3)和线性代数的有关知识可知,当行列式det(KE+λPkg) =0 时,杆件会发生屈曲。 根据det(KE+λPkg) =0,可求解出不同的特征值λ,特征值λ被称为屈曲因子(某些分析软件将其成为临界系数)。 求出特征值之后,可知临界荷载Pcr=λP,如果内力和外力的关系不是简单的相等关系,Pcr可以转换得到。 式(3)的计算结果要想获得足够的精度,一根杆件应至少划分为两个单位,利用式(3)求解临界荷载的过程是一种有限元方法,一般要通过分析软件实现,这种方法一般称其为线性屈曲分析,与P相关的初始加载工况在一些软件中被称为屈曲分析荷载组合。
3.2 计算长度的求解方法
实际工程中线性屈曲分析依据不同对象,分为整体模型法和独立杆件模型(局部模型)法。
整体模型法是对整个结构模型进行线性屈曲分析的一种方法,它的分析结果可以直观的反映整个结构的屈曲变形,能观察出构件失稳的先后顺序,对结构整体稳定性的评价有一定帮助。 通过式(2)可知屈曲分析的加载方式会影响各个构件的初始几何刚度,进而影响分析结构,因此应取用反映结构实际工作状态时的工况来加载。 整体模型法的分析结果不能直接获得某个杆件的杆端失稳临界荷载,因为并没有这样一个轴向力施加在实际模型的杆件端部。 整体模型法可以获得该杆件在失稳临界状态下的杆端轴力,然后通过杆端轴力与杆端单位轴向荷载(外荷载)的关系,求得Pcr,进而求得计算长度系数μ。 整体模型法步骤明确,容易理解,得到的结果较为准确。
当结构模型较为复杂,杆件节点较多时,整体模型法有分析计算量很大,耗时较多。 如果结构的不规则性较为明显,刚度分布过于离散,整体模型法可能无法得到这类模型中某些杆件的屈曲模态。 为了获得这类杆件的屈曲模态,可以建立一个只有一根杆件的模型(或者局部几根杆件),然后根据整体模型中的实际约束情况,建立边界条件,在杆端施加单位轴向荷载,进行屈曲分析,这样通常就可获得待分析杆件的屈曲模态了,这种分析方法就是独立杆件模型法。 这种方法的关键是要合理的建立边界条件,可以通过单位力或力偶下整体模型中待分析杆件杆端的位移和转角的倒数作为支座刚度,建立边界条件,但是这种方法无法考虑约束刚度的耦联,因此会造成一定的误差。 此外,独立杆件法的加载方式和整体模型中构件的工作工况相差较多,这也会造成误差。 一般情况下,井架线性屈曲分析的屈曲模态是容易获得的,如果确实出现了无法获得构件屈曲模态的情况,可以采用独立杆件模型法,这种方法结果可能是偏于保守的。
4 工程实例中的计算长度系数求解
前面的内容已经介绍了屈曲分析求钢井架计算长度系数的基本原理,实际工程中计算长度的求解一般可分五个步骤进行。
①建立结构模型;
②建立分析工况,加载,进行整体模型的屈曲分析,找寻需要的屈曲模态和临界荷载系数(如果无法获得需要的屈曲模态应采用独立杆件模型法进行分析);
③查看加载工况的初始杆端轴力(内力),计算屈曲状态下的杆端轴力(内力);
④根据近似关系求杆端临界轴力(外力);
⑤利用欧拉公式求计算长度系数。
以下将详细介绍某实际工程双斜撑钢井架利用有限元分析软件MIDAS GEN 对整体模型屈曲分析求解该结构中斜撑柱计算长度系数的过程。
4.1 工程概况
某6 度区副井井架,设两套提升系统:大罐笼+平衡锤提升,小罐笼+平衡锤提升。 大罐笼提升导向天轮直径6 m,中心高度分别为∇35.850 m 和∇45.850 m,钢丝绳最大静张力1 917 kN, 静张力差148 kN,钢丝破断拉力总和为6 ×2 845 kN。 小罐笼提升导向天轮直径4.5 m,中心高度分别为∇37.000 m 和∇45.000 m,钢丝绳最大静张力654 kN,静张力差49 kN,轮钢丝破断拉力总和4 ×1 450 kN。大小提升系统中心线位于同一平面,二者夹角为180°。
4.2 求解斜撑柱计算长度的步骤
(1)进行结构配置,建立结构模型。 钢井架结构配置的基本原则是满足工艺需求和总图平面布置的情况下,尽可能使斜架中心线与提升机钢丝绳合力线之间的夹角减少,以尽量减少荷载偏心对结构造成扭矩和弯矩。 钢井架通常采用空间杆系模型,在midas gen 中可采用梁单元对构件进行模拟,天轮梁等异形构件应采用软件中的任意截面计算器进行定义。 斜撑柱支座采用铰接。 钢井架有限元模型如图1 所示。 杆件2,4,6,8,23,25,41,43,56,58 是大天轮一侧的斜撑柱构件。 杆件1,3,5,7,22,24,40,42,55,57 是小天轮一侧的斜撑柱杆件。 斜撑柱截面:箱型2 500 ×2 500 ×25。 钢井架的杆件细分模型如图2 所示。 本设计中立架顶部与斜架平台梁采用滑动连接,但立架自身与采用钢框架-支撑体系,因此可认为斜架不需要给立架提供抗侧刚度,进行斜撑柱的屈曲分析的模型可不考虑立架。

图1 结构杆件编号

图2 杆件细分模型
(2)进行屈曲分析。 通过式(3)可知,加载方式会影响结构的初始几何刚度矩阵,不同的屈曲分析荷载组合会得到不同的分析结果。 按照设计经验,井架可按“1.3(结构自重+天轮自重) +1.5 天轮工作荷载”的荷载组合加载,模态数量设定为30。 本工程各阶屈曲模态具有以下特点:第一阶模态是大天轮一侧上天轮梁的局部屈曲,其余构件未发生变形;第二阶和第三阶屈曲模态,钢井架分别发生了平面内和平面外的整体屈曲;第四阶和第五阶屈曲模态,杆件2,4 分别发生平面内和平面外屈曲。 第七阶模态,杆件1,3 首次发生平面外屈曲。 第八阶模态,杆件1,3 首次发生平面内屈曲;第十三阶模态,支承天轮梁的斜撑杆件23,25,41,43 以及22,24,40,42 首次发生了平面内屈曲,杆件2 和杆件4 产生了带反弯点的屈曲。 第十六阶模态,大天轮一侧支承天轮梁的斜撑杆件23,25,41,43 首次发生平面外屈曲。 第二十四阶模态,小天轮一侧支承天轮梁的斜撑杆件22,24,40,42 首次发生平面外屈曲;其余各模态均是杆件首次屈曲之后的更高阶屈曲模态。 屈曲模态的使用应注意以下两点:①应使用某一构件首次发生构件屈曲时的临界系数进行后续计算,因为通过式(2)可知临界荷载越小,对应的计算长度系数越大,说明构件越容易失稳;②一般不使用整体屈曲的临界系数进行后续分析。 典型的屈曲模态如图3 至图12 所示。 典型模态的屈曲因子见表1。

表1 典型模态的屈曲因子

图3 模态1
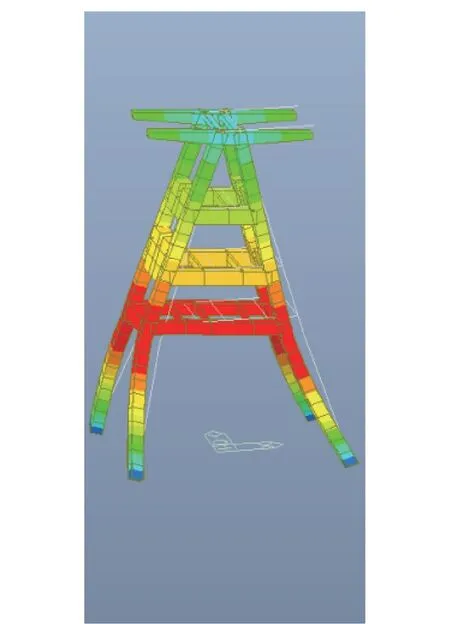
图4 模态2
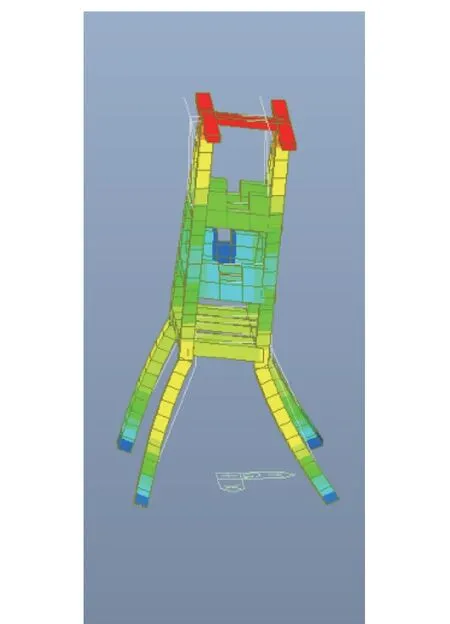
图5 模态3

图6 模态4

图7 模态5

图8 模态7

图9 模态8

图10 模态13
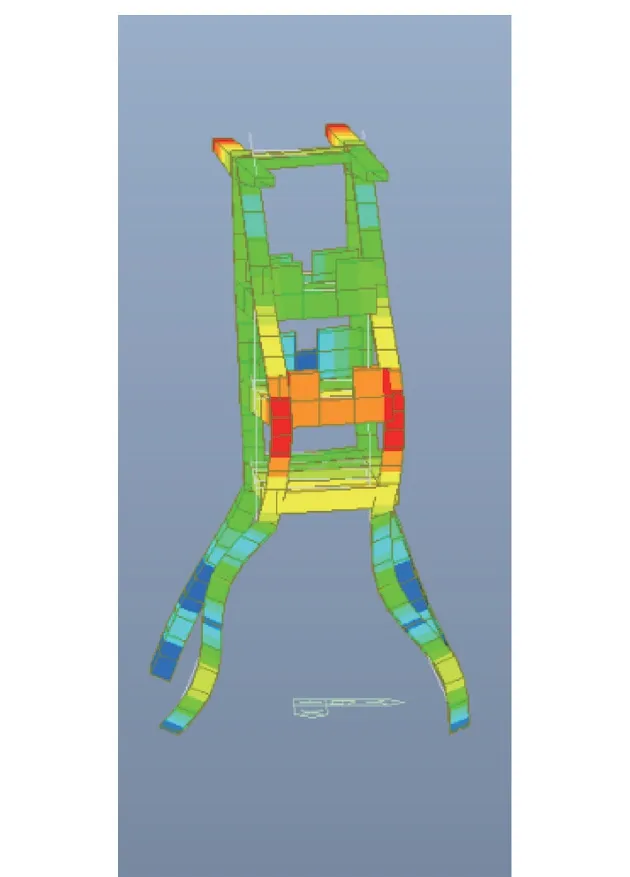
图11 模态16
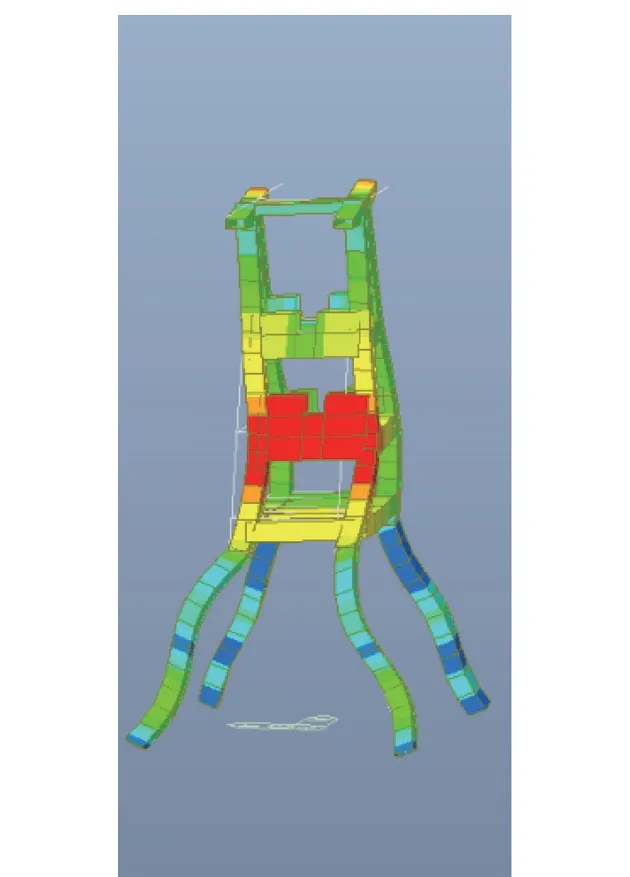
图12 模态24
(3)计算构件临界杆端轴力Ncr(内力)。 首先提取自重工况2 号杆件杆端轴力2 458.81 kN,天轮自重工况的杆端轴533.417 kN 以及天轮工作荷载工况对应的杆端轴力3 993.36 kN。 杆端初始状态轴力组合值:1.3 ×2 458.81 +1.3 ×533.417 +1.5 ×3 993.36 =9 879.973 kN。Ncr=屈曲因子×轴力组合值,根据上一步骤可知2 号杆件在第四模态发生平面内屈曲,在第五模态发生平面外屈曲,分别取用这两个模态的临界荷载系数进行计算:Ncr(平面内) =57.70 ×9 879.973 =570 074 kN。Ncr(平面外) = 68.62 ×9 879.973 =677 964 kN。
(4)计算杆端临界荷载Pcr(外力)。 欧拉公式的计算模型是在杆端外荷载下的杆件屈曲。 由于实际的模型中并不会在2 号杆件的杆端作用一个外荷载,因此需要考察整体模型中单位外荷载作用下的杆端轴力(内力),以此作为杆件内力和外荷载的转换系数。 2 号杆件在杆端单位轴向力工况下的杆端轴力为查看此单位荷载下杆端轴力为0.973 8 kN,此轴力将作为杆件2 的转换系数,具体如图13 所示。 施加节点单位轴向外荷载时,可采用将沿杆件轴向单位力分解为三个沿坐标轴方向分力的方式,这是一种更加方便的操作。Pcr(平面内) =Ncr(平面内)/0.973 8 =585 411 kN;Pcr(平面内) =Ncr(平面外)/0.973 8 =69 620 kN。
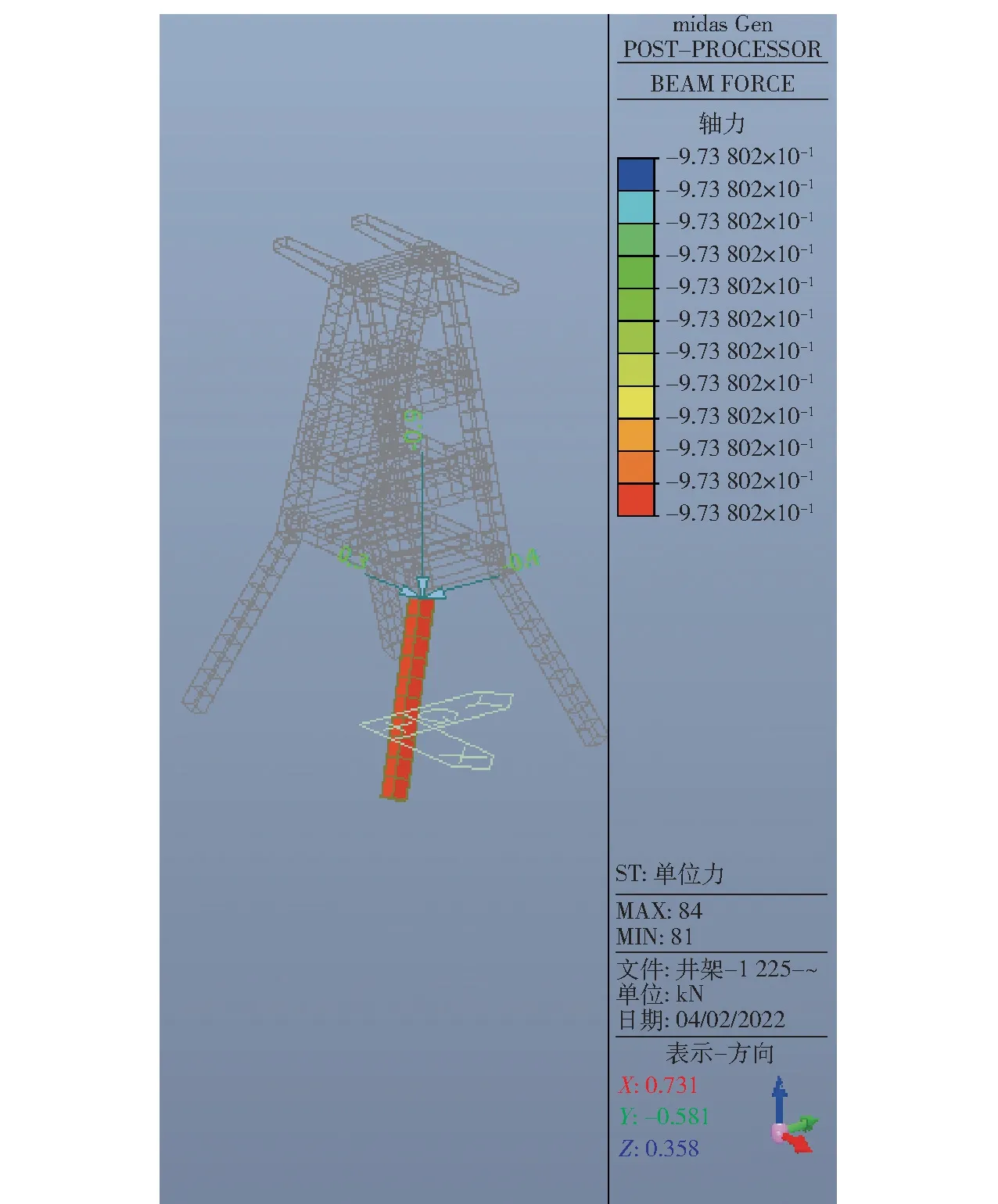
图13 单位力作用目标杆件杆端轴力
(5)将杆端临界荷载带入式(2),可求出目标杆件平面内计算长度系数μ(平面内)=0.956 4 平面外计算长度系数μ(平面内)=0.877 0。 至此,2 号杆件的计算长度系数求解完毕。 结构其他杆件计算长度系数的求解过程与2 号杆件的过程一致。
4.3 屈曲分析注意事项
不同加载模式,会产生不同的分析结果,目前并没有相关标准,设计者可根据自己的经验自行设定屈曲分析工况。 但不建议加载断绳荷载,按设计经验,这可能会导致算出的计算长度系数偏小。
屈曲分析求出的井架斜撑的计算长度系数,建议乘以及一个放大系数1.1,作为安全储备。
应关注屈曲模态发生的先后顺序,斜撑柱的屈曲应滞后于结构整体屈曲,否则应加强斜撑柱的刚度。
天轮梁以上的斜撑构件由于不承受较大的天轮工作荷载,其屈曲模态不是很容易获得,但这也说明,这部分构件不容易失稳,这类构件的计算长度系数可直接取井架规范中的下限值。
杆件单元的划分会影响屈曲分析的结果,每个斜撑柱构件的单位划分建议不少于五个。
5 结论
一阶弹性分析法仍是在矿山工程结构设计中被广泛使用的一种方法,计算长度系数是该方法应用所需的重要参数。 现行《井架标准》中对斜撑柱计算长度系数的求解方法规定概念性较强,应用性较差。 本文介绍了利用屈曲分析和欧拉公式求解钢井架空间斜撑柱计算长度系数的方法步骤以及注意事项,可为类似问题提供应用参考。
