一种新型可变增益高阶滑模跟踪微分器

赵左平， 于靖东， 金山海

( 延边大学 工学院， 吉林 延吉 133002 )

0 引言

在反馈控制系统中，反馈回路通常由输入信号及其导数构成.但由于受环境干扰和传感器精度等的影响，反馈回路中的输入信号易含有噪声，进而会降低系统的控制性能；因此,滤除输入信号中的噪声并正确估计其导数对系统控制具有重要意义.目前，数字滤波技术已被广泛应用于数字控制系统中，其中线性滤波器因具有结构简单的优点受到学者们的关注；但线性滤波器在强降噪的情况下会产生较大的相位滞后，进而会降低控制系统的稳定性.针对线性滤波器所存在的缺陷，一些学者对非线性滤波器进行了研究.1994年，韩京清等[1]提出了一类具有抛物线滑模面的2阶滑模跟踪微分器(TD- [1])，由于该滤波器的滤波效果显著优于线性滤波器，因此目前被广泛应用于各类控制系统中[2-4].但TD- [1]存在易产生超调的缺陷，对此Jin等[5]对TD- [1]进行了改进并提出了TD- [5]，该方法可有效对超调进行抑制.Lü等[6]在TD- [5]的基础上提出了一种快速收敛的2阶滑模跟踪微分器(TD- [6])，TD- [6]可在不影响滤波效果的前提下提高系统状态的收敛速度.由于上述微分器都只能估计输入信号及其1阶导数，而无法估计输入信号的高阶导数，因此Levant[7]研究了另一类能估计输入信号高阶导数的高阶滑模跟踪微分器(TD- [7]).TD- [7]虽具有高鲁棒性、高精确性等优点[8-10]，但其在响应阶段会产生较大超调，且在强噪声情况下无法平衡滤波效果和跟踪速度之间的权衡.为此，本文对TD- [7]进行改进，提出一种新型可变增益高阶滑模跟踪微分器，并对其性能进行了研究.

1 高阶滑模跟踪微分器

TD- [7]的连续时间表达式为：

(1a)

…

(1b)

(1c)

(1d)

…

(1e)

(1f)

其中:nf=1,2,3,…;nd=0,1,2,3,…;k=1,2,3,…;nf+nd=k;u(t)为输入信号;z0(t),z1(t),…,znd(t)为输入信号u(t)的nd阶导数估计；w1(t),w2(t),…,wnf(t)为辅助变量；λ0,λ1,λ2,…,λk>0是一组递归数列；L>0为系统增益；符号函数sgn()的表达式为：

(2)

图1为1阶TD - [7]在含噪声阶跃输入信号时的响应结果.由图1可以看出，系统增益L取任何值时都会产生超调.另外，增大L值虽然可加快系统的收敛速度，但同时会降低滤波效果，因此需要平衡系统的响应速度与滤波效果.

2 新型高阶滑模跟踪微分器

2.1 改进型高阶滑模跟踪微分器

本文提出的改进型高阶滑模跟踪微分器(TD - M)的连续时间表达式为：

(3a)

…

(3b)

(3c)

(3d)

…

(3e)

(3f)

其中0 <β≤1.

图2为1阶TD- [7](L=100)和1阶TD -M(L=375,β=0.5)在无噪声阶跃输入信号时的响应结果.图2中，为了使TD- [7]和TD - M的收敛速度相同，本文增加了TD - M的增益取值.由图2可以看出，在t1时刻之前，z0(t)-u(t)的符号未发生改变，因此w1(t)始终朝一个方向进行累积；在t1时刻之后，z0(t)-u(t)的符号发生改变，且此时w1(t)已经累积了一定数值，因此w1(t)的符号在t2时刻才能发生改变并需要一定的时间才能收敛到0.由以上可知，TD - [7]和TD - M都会产生超调，但由于TD - M的各阶系统状态都增加了β项，因此w1(t)的改变点相比TD - [7]出现得更早,且收敛到0的速度更快，即TD - M在系统响应阶段所产生的超调小于TD- [7].

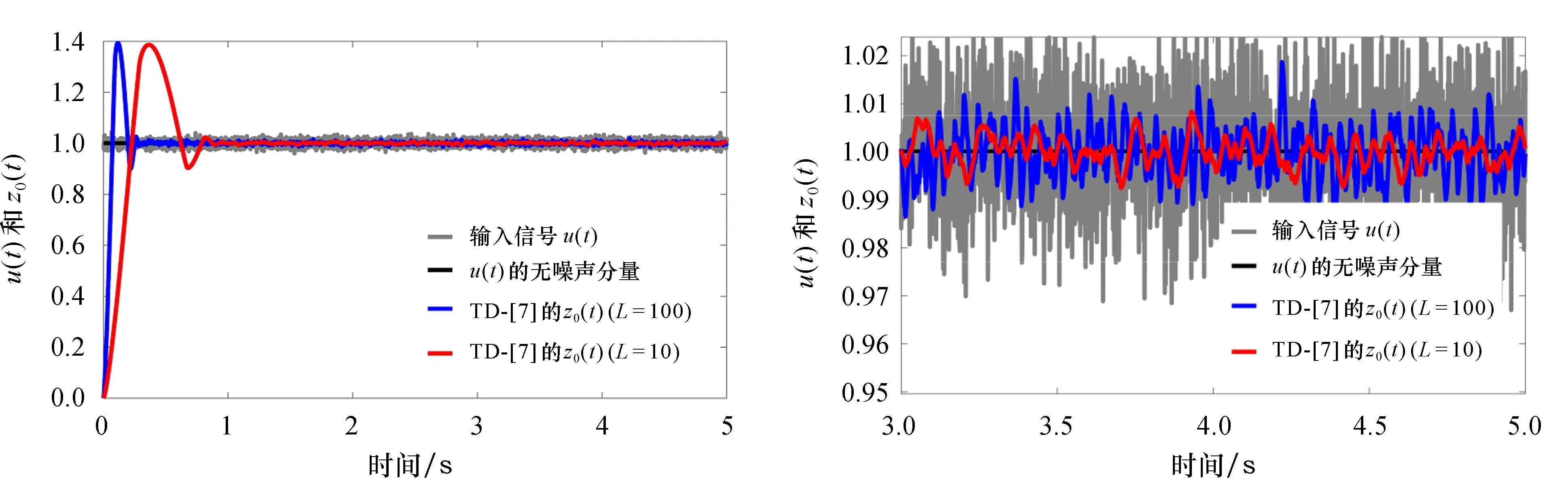
(a) 输入信号u(t)和输出信号z0(t) (b) 图(a)的局部放大 图1 TD - [7]在含噪声阶跃输入信号时的响应结果

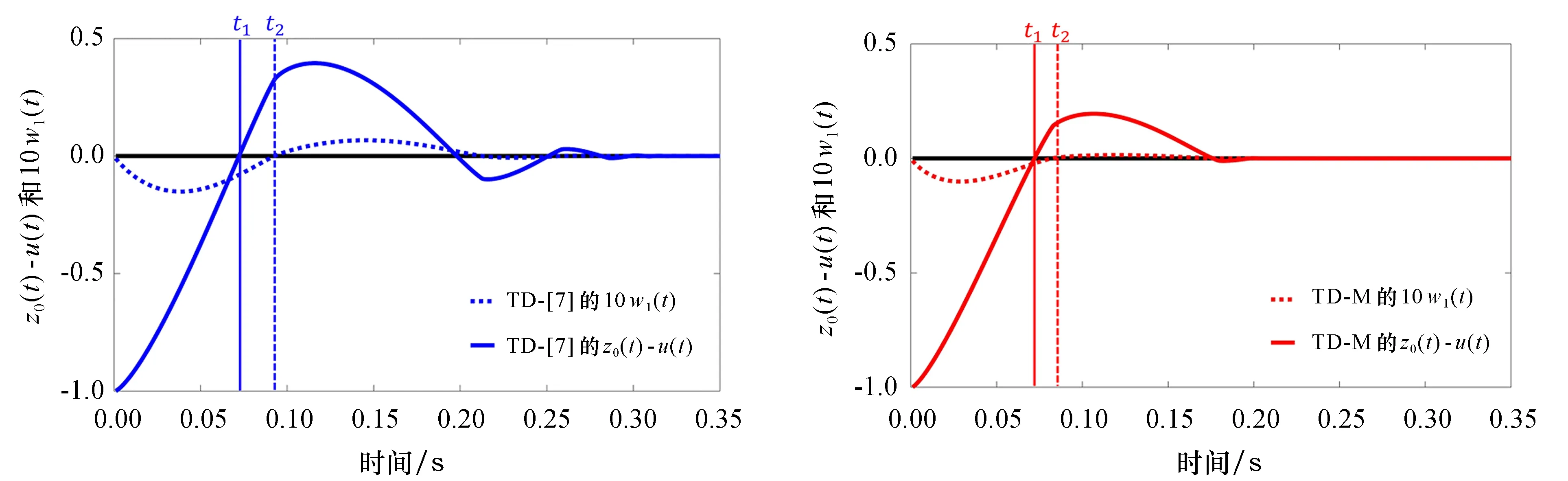
(a) TD- [7]的z0(t)-u(t)和10w1(t) (b) TD - M的z0(t)-u(t)和10w1(t)图2 1阶TD - [7]和1阶TD - M在无噪声阶跃输入信号时的响应结果

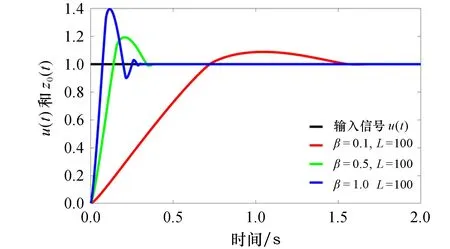
图3 1阶TD - M在无噪声阶跃输入信号下β取不同值时的响应结果

图3为1阶TD - M在无噪声阶跃输入信号下取不同β值的响应结果.由图3可以看出，增益L值不变时系统的收敛速度和超调均随β值的减小而减小.

图4为1阶TD - [7](L=100)和1阶TD - M (L=375,β=0.5)在含噪声阶跃输入信号时的响应结果.由图4可见，二者在响应速度相近时TD - M产生的超调小于TD - [7]，但在稳态阶段下二者的滤波效果相似.

(a) TD - [7]的z0(t)和TD -M的z0(t) (b) 图(a)的局部放大 图4 1阶TD - [7]和1阶TD - M在含噪声阶跃输入信号时的响应结果

2.2 可变增益高阶滑模跟踪微分器

为了进一步提升TD- M的噪声抑制能力，本文提出了一种可变增益高阶滑模跟踪微分器(TD- N)，即用Sigmoid变增益函数代替常数增益L对系统的跟踪性能进行调整.利用该方法可使系统在跟踪误差较大时，能够通过增大增益来提高收敛速度，而在跟踪误差较小时能够通过减小增益来提高滤波效果.TD- N的连续时间表达式为：

(4a)

…

(4b)

(4c)

(4d)

…

(4e)

(4f)

图5为参数a和b取不同值时Sigmoid变增益函数的变化曲线.由图5可以看出，通过调节参数a可改变Sigmoid变增益函数的斜率，通过调节参数b可改变Sigmoid变增益函数的下限.

图5 参数a和b取不同值时Sigmoid变增益函数的曲线变化

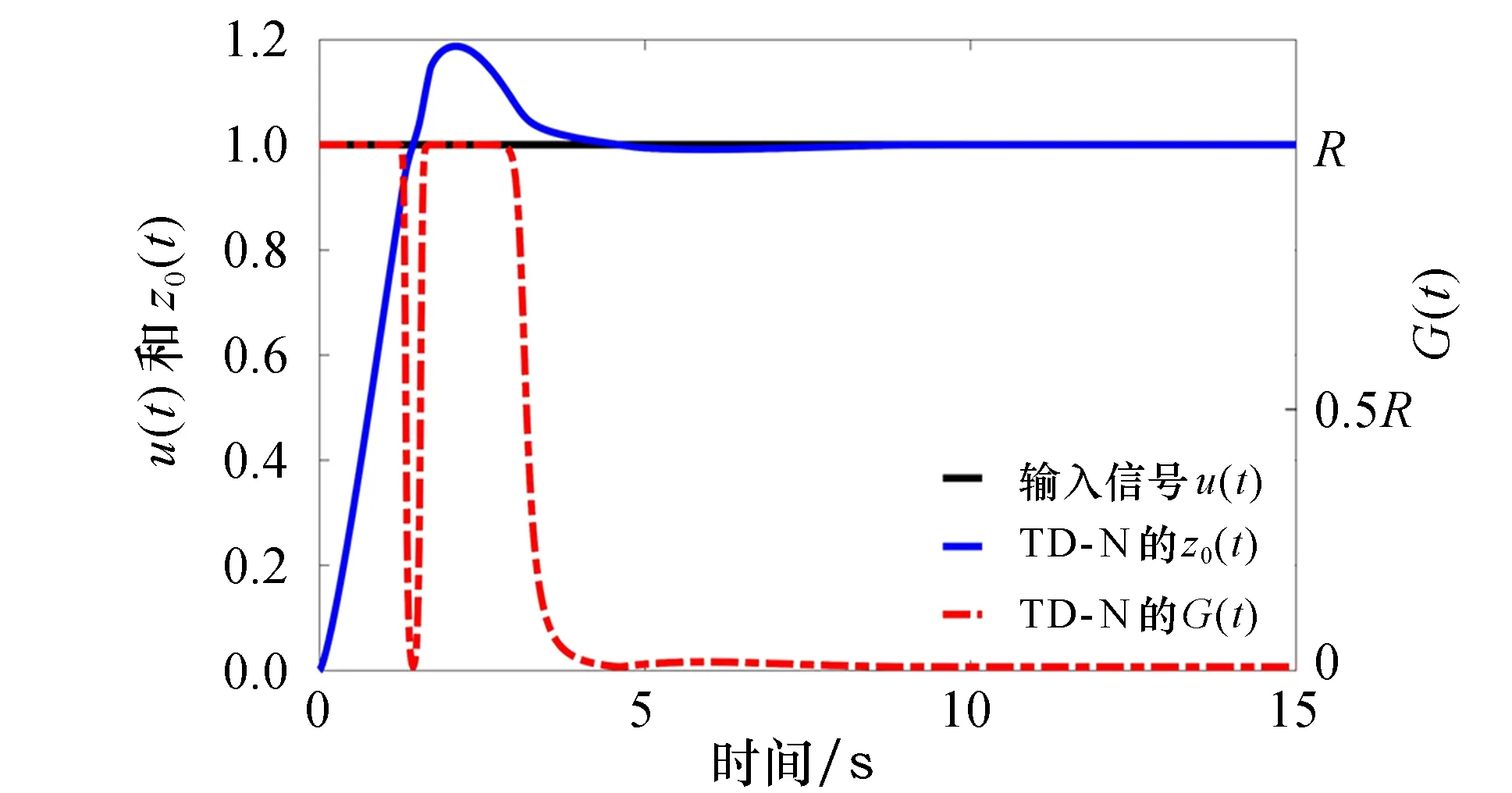
图6 TD - N在无噪声阶跃输入信号时的响应结果

图6为TD - N在无噪声阶跃输入信号时的响应结果.从图可以看出，当跟踪误差较大时，系统处于响应阶段.此时函数G(t)的值无限趋近于上限，从而可加快系统的状态收敛.而当系统趋于稳态和跟踪误差较小时，函数G(t)的值趋于下限，从而可提高滤波效果.

3 仿真验证

本文采用如下三角波、方波及变频正弦波输入信号对TD - N的有效性进行验证：

(5)

(6)

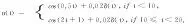
(7)

其中：δ(t)～N(0,1)是均值为零的单位高斯白噪声.TD - [7]和TD - N的参数取值见表1，仿真采样周期取T=0.001 s.此外，由于TD - [7]的连续时间表达式(1)和TD - N的连续时间表达式(4)无法在数字处理器中直接运行，因此采用前进欧拉离散法对其进行离散化后再在数字处理器中进行运行[12].

表1 TD - [7]和TD - N的参数取值

使用以下两个评估函数定量评估系统的滤波效果和超调量：

式中:AE是平均误差，us(t)为输入信号的无噪声分量，MO是最大超调量.

图7—图15分别为TD- [7]、TD- N在输入信号为式(5)—(7)时的性能. 由图可以看出，在该3种输入信号下，TD- N和TD- [7]的收敛速度虽然接近，但TD- N的最大超调量明显小于TD- [7].此外，在稳态阶段TD- N的滤波性能也显著优于TD- [7].由此可知，在不影响收敛速度的前提下 TD- N的超调抑制能力和噪声滤除能力均优于TD- [7].

图7 输入信号为式(5)时TD- [7]和TD- N的响应结果

图9 输入信号为式(7)时TD- [7]和TD- N的响应结果

图10输入信号为式(5)时TD- [7]和TD- N的平均误差

图11输入信号为式(6)时TD- [7]和TD- N的平均误差

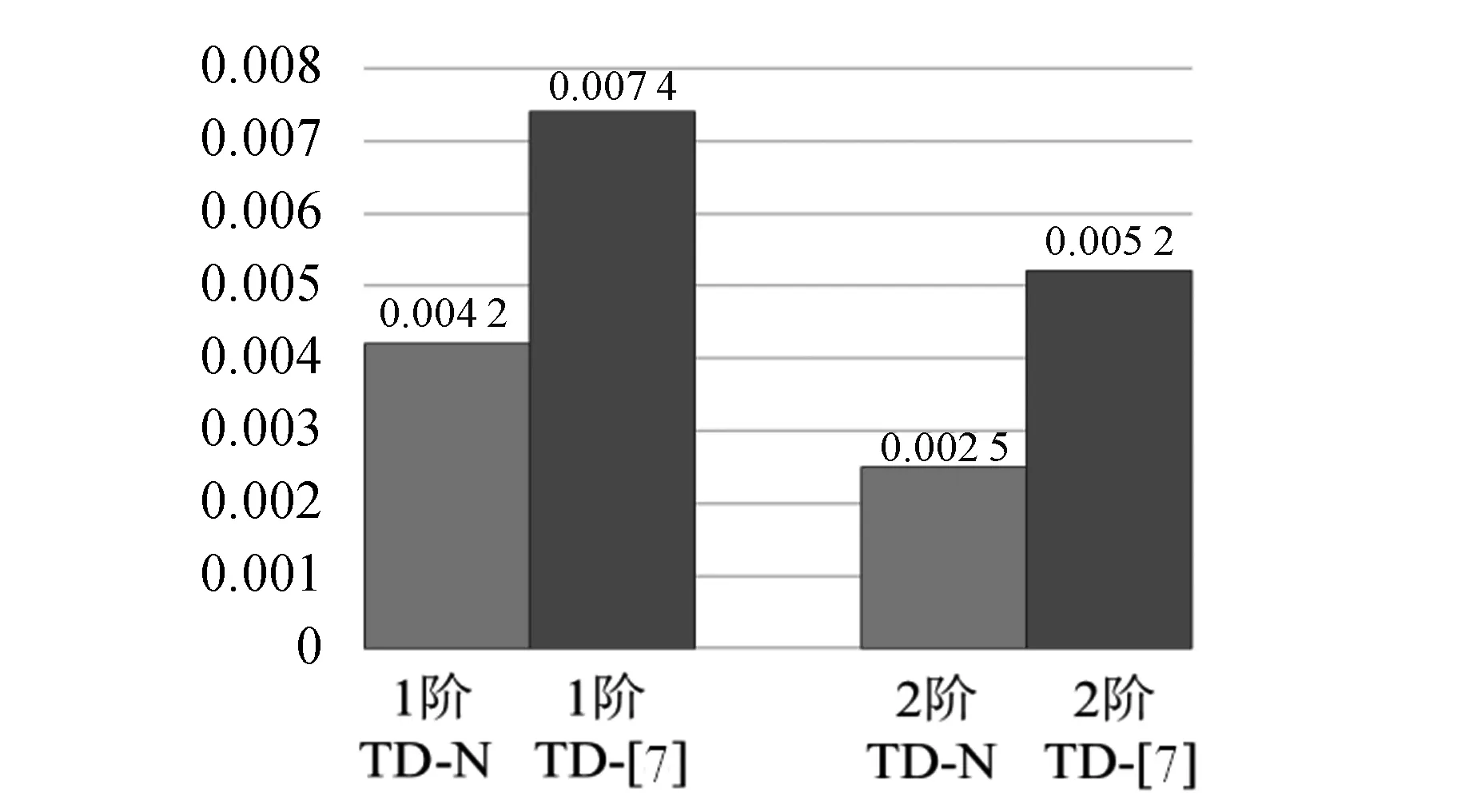
图12输入信号为式(7)时TD- [7]和TD- N的平均误差

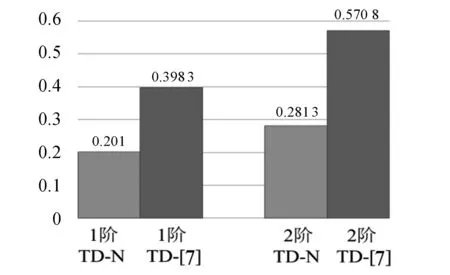
图14输入信号为式(6)时TD- [7]和TD- N的最大超调量

图13输入信号为式(5)时TD- [7]和TD- N的最大超调量

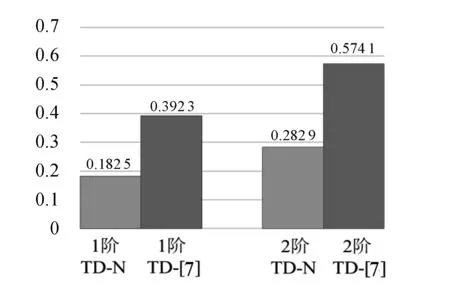
图15输入信号为式(7)时TD- [7]和TD- N的最大超调量

4 结论

研究表明，本文提出的新型可变增益高阶滑模跟踪微分器(TD- N)产生的超调不仅小于TD- [7]，而且在不影响收敛速度的前提下可有效提高滤波效果；因此，TD- N的性能显著优于TD- [7]， 并有望在强噪声和宽输入信号频率的环境下得到应用.本文在研究中仅对TD- N的部分参数进行了分析，因此在今后的工作中我们将进一步研究其他参数对TD- N的性能的影响，以得到更好的TD- N.