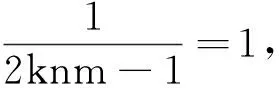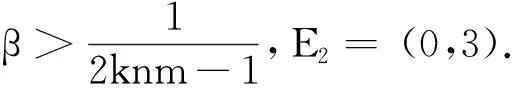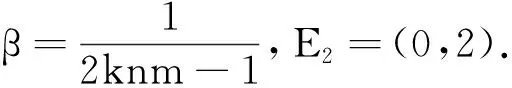一类具有附加食物的Leslic - Gower捕食者 食饵模型的定性分析
2022-09-13吴罗义
吴罗义
( 武夷学院 数学与计算机学院, 福建 武夷山 354300 )
0 引言
捕食者- 食饵系统是生物数学研究的重要对象之一.从捕食者的生长函数与捕食函数关系考虑,可将相应的捕食者-食饵模型分为两类:一类是捕食者的生长函数与捕食函数一致,如经典的Gause型模型[1];另一类是捕食者的生长函数与捕食函数不同,如Leslie - Gower模型[2]:
(1)
其中u(t)和v(t)分别为食饵和捕食者的密度,其他参数为正常数(生物意义参考文献[2]).Hsu等[3]研究表明,模型(1)的唯一正平衡在所有生物学允许的参数内是渐近稳定的.为了研究不同捕食功能函数以及物种在较大范围内的空间移动对模型(1)的影响,一些学者对模型(1)进行了改进.例如: Huang[4]等提出了一类具有广义Holling III功能反应的Leslie模型,并证明了该模型在两个退化平衡点处分别经历了亚临界Hopf分支和Bogdanov - Takens分支;张丽娜等[5]提出了一类修正的Leslie - Gower捕食者- 食饵扩散模型,并研究了该模型正平衡点的全局渐近稳定性;鲁引儿等[6]研究了一类具有非线性收获的Leslie - Gower捕食者- 食饵扩散模型,并讨论了其Hopf分支的存在性.
在模型(1)中,如果食饵是害虫,则害虫是不可能被消灭的(模型(1)不存在食饵灭绝的平衡点).研究表明,给捕食者提供额外食物可使模型产生食饵灭绝的平衡点.例如: Basheer等[7]在Holling - Tanner模型的基础上建立了一类提供额外食物的Holling - Tanner模型,并研究了附加食物对食饵种群的影响.本文根据文献[7]的建模机理,在假定捕食者对食饵与附加食物的选择无偏好的基础上,将模型(1)改进为如下形式:
(2)
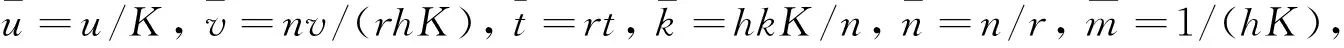
(3)
本文将研究模型(3)的局部与全局渐进稳定性,以及非双曲平衡点在适当参数扰动下所产生的分支等动力学行为.
1 平衡点的局部稳定性

对J(E0)和J(E1)的特征值进行计算可知,E0(0,0)是不稳定的结点,E1(1,0)是鞍点.


(4)
对式(4)作线性变换(U=x,V=nx+y)可得:
(5)

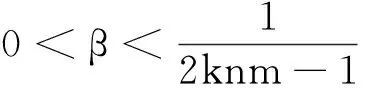
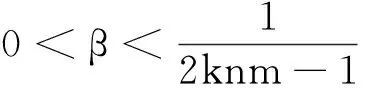

2 分支分析

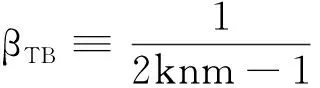

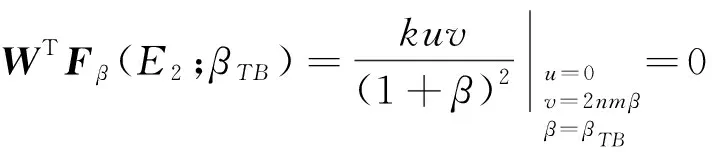
WT[DFβ(E2;βTB)V]=

于是由Sotomayor定理[8]可知,系统在β=βTB处围绕E2存在跨临界分支,即当参数β从βTB的一端跨越到另一端时,E2的稳定性发生改变.
3 全局稳定性
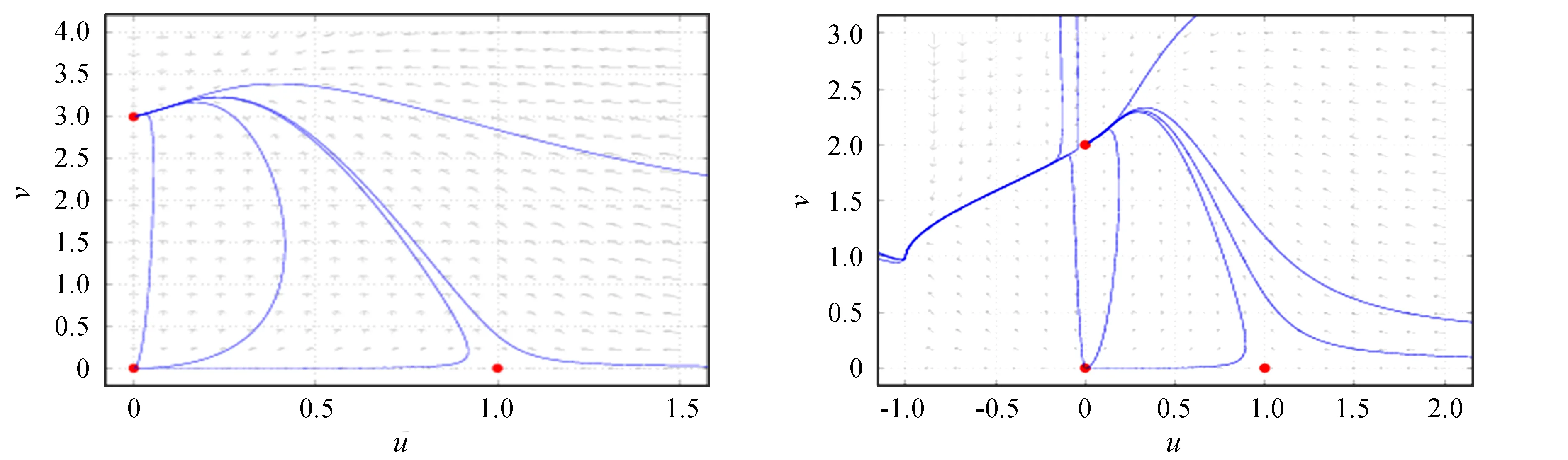
引理1系统(3)是最终有界的,且Ω={(u,v)|0 上式说明当v≤2mnβ时,捕食者总是递增的,即当t充分大时v≥2mnβ. 引理2系统(3)在R2+上不存在闭轨. 证明取Dulac函数B(u,v)=uα -1vγ -1, 其中α和γ为待定常数,则有: 定理5当0<β<1/(2kmn-1)时,E3在R2+上全局渐进稳定. (6) 图1 β=1.5时系统(6)的相图 图2 β=1.0时系统(6)的相图 图3 β=0.5时系统(6)的相图
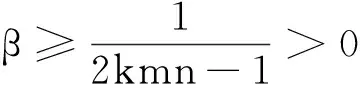
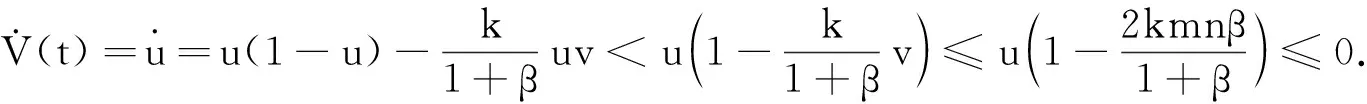
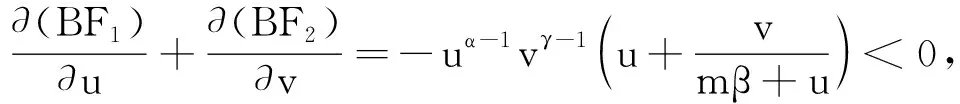

4 数值模拟