基于概率语言组合赋权与MULTIMOORA的多准则决策方法
2022-09-13曾凡龙倪静阮俊华王耀燕
曾凡龙, 倪静, 阮俊华, 王耀燕
( 1.义乌工商职业技术学院, 浙江 义乌 322000; 2.上海理工大学 管理学院, 上海 200093;3.马来亚大学 工程学院, 吉隆坡 50603 )
0 引言
2010年, Brauers等[1]以比例分析多目标优化法(MOORA)为基础,通过增加全乘模型和借鉴占优理论提出了MULTIMOORA法.由于该方法具有运算时间短、决策复杂度低、鲁棒性强等优点,因此被应用于多个领域中,如食品废弃物处理方案选择[2]、应急救援方案搜索[3]、高强混凝土性能评价[4]等.但目前为止采用MULTIMOORA方法进行多准则决策时大多是针对定量信息进行的,缺乏对评价信息的模糊性和不确定性的探讨.对此, Arian等[5]采用模糊集方法研究了MULTIMOORA中的评价信息,但该方法无法表征集合中元素的模糊性.Zhang等[6]和周文财等[7]分别采用单一的三角模糊数和直觉模糊数研究了MULTIMOORA中的评价信息,该方法虽然可以处理决策信息的不确定问题,但单一的模糊数难以全面表征决策者的意见.Liang等[8]使用犹豫语言模糊集(HFLTS)研究了MULTIMOORA中的评价信息,该方法虽然能够体现决策者的犹豫性,但无法表征决策者对语义集的不同偏好.Pang等[9]基于HFLTS提出了概率语言术语集(PLTS), 研究显示利用PLTS对语义集赋予相应的概率可较好地体现决策者的犹豫度以及偏好度,进而可较为准确地表征评价信息中的模糊性和不确定性.
为了更好地获得MULTIMOORA方法中各评价准则的权重, Baidya等[10]将CRITIC客观赋权法引入到MULTIMOORA中,该方法虽然计算简便,但缺乏对评价者的主观意愿评价.Fattahi等[11]采用AHP法改进了MULTIMOORA方法的权重确定准则,该方法虽然考虑了决策者的主观意愿,但当评价准则较多时存在评价过于繁琐的问题,且难以满足一致性检验.翟强等提出了G1法,该方法不仅能保证评价结果的可靠性,而且过程简单,同时还可解决AHP方法难以构造一致性判断矩阵的问题[12].基于上述研究,本文在引入概率语言的基础上,结合主观和客观赋权法的优势构建了一种G1 - CRITIC组合优化赋权模型,并利用该模型对MULTIMOORA法进行了改进,同时采用案例验证了改进方法的有效性.
1 PLTS的基本概念
PLTS是由语义集及其对应的概率组成的语义集合,它不仅可描述决策者在评价方案时的犹豫情形,而且还可表达决策者的偏好程度.
定义1[13]设S={s0,…,sα}为一个LTS, 则一个PLTS可以被定义为:
L(P)={L(x)(p(x))|L(x)∈S,x=1,2,…,#L(p)}.
(1)
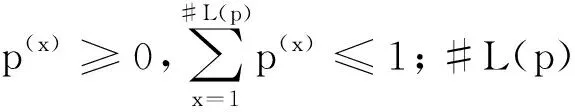
如:设LTS是一个5个粒度的语言术语集,S5={S0=VL,S1=L,S2=M,S3=H,S4=VH}.当准则为立体仓库智能化设计方案的高效性(C1)时,决策者认为该准则为“绝大多数时候对选择结果有很大影响,仅偶尔会有一般影响”,则此时记“绝大多数时候对选择结果有很大影响”为S4, 其概率为0.8, 记“仅偶尔有一般影响”为S2, 其概率为0.1, 此时的L(p)={(S4,0.8),(S2,0.1)}.


(2)

定义3[14]设L(p)={L(x)(p(x))|x=1,2,…,#L(p)}为一个PLTS,r(x)为语义集L(x)的下标,则L(p)的得分函数为:
(3)


(4)
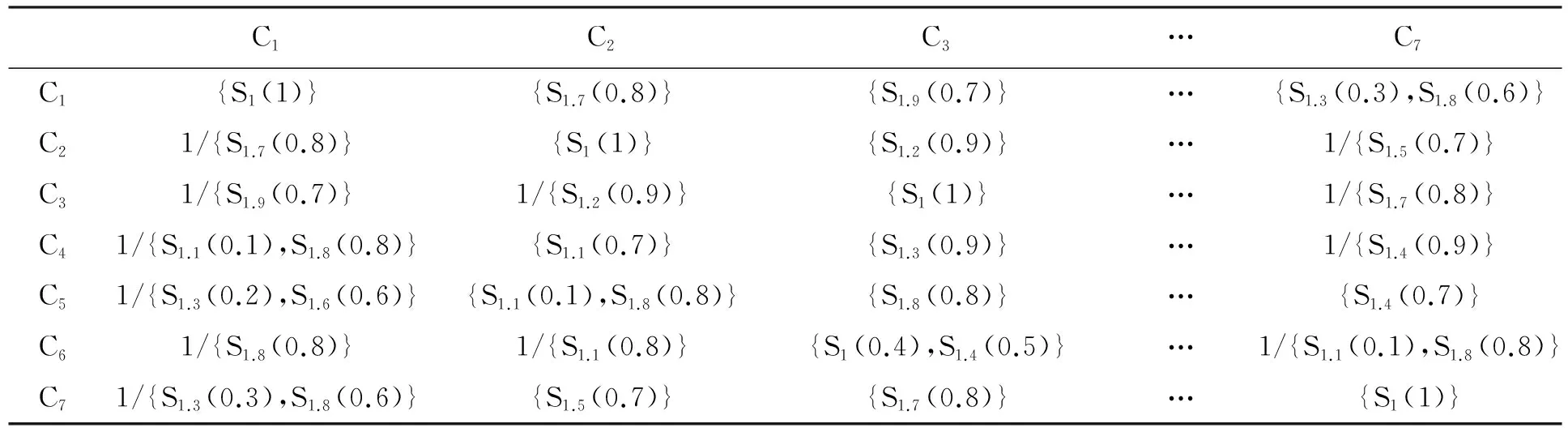
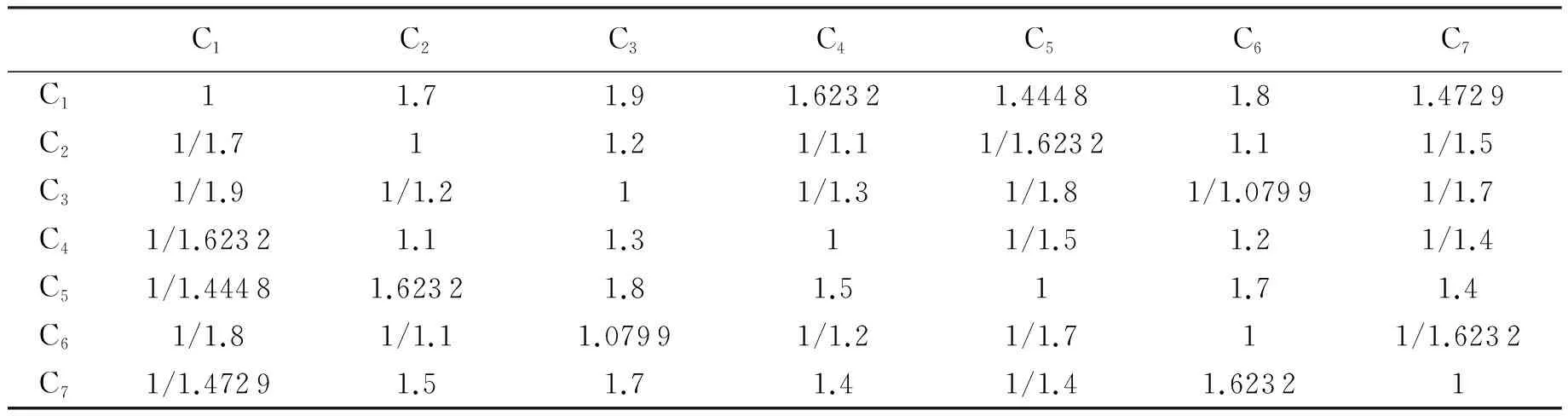
设概率语言术语集L(p)1和L(p)2的得分函数分别为G(L(p)1)和G(L(p)2), 且其偏差度分别为σ(L(p)1)和σ(L(p)2).当G(L(p)1)=G(L(p)2)时,若σ(L(p)1)<σ(L(p)2), 则L(p)1>L(p)2; 若σ(L(p)1)=σ(L(p)2), 则L(p1)=L(p2); 若σ(L(p)1)>σ(L(p)2), 则L(p1) 定义5[14]设S={s0,…,sα}为一个LTS,L(p)={L(x)(p(x))|x=1,2,…,#L(p)}为一个PLTS,语义集L(x)的下标是r(x),L(p)中语义集L(x)的粒度越大表示评价时越犹豫,则L(p)的犹豫度为: (5) 定义6[14]设L(p)={L(x)(p(x))|x=1,2,…,#L(p)}为一个PLTS, 则将L(p)转化为精确数值的转化函数为: (6) 2.1.1基于概率语言G1法的主观权重确定 表1 G1中的概率语言粒度含义 采用概率语言改进G1法求解各准则主观权重的步骤为: 2)相邻准则的重要性判断.首先由决策者采用概率语言对相邻评价准则的重要程度之比进行判断,然后采用式(3)—(6)将概率语言术语转化为精确值γk(γk为经过概率语言转换的相邻准则的重要性程度的比值): (7) (8) 2.1.2基于概率语言CRITIC法的客观权重确定 CRITIC法是一种考虑了样本的对比强度和指标间冲突性的客观赋权方法,但其权重计算缺乏灵活性,且过于依赖样本数据;因此,本文采用概率语言对CRITIC法进行改进,以此确定概率语言在CRITIC法下的粒度.如:设PLTS为一个9粒度的术语集(粒度含义如表2所示),L(p)={(S7,0.8),(S6,0.2)}表示为“绝大多数时备选方案Ai在准则Cj中评价值高,仅偶尔时评价值稍高”. 表2 CRITIC中的不同概率语言粒度的含义 本文基于概率语言CRITIC法计算评价准则客观权重的步骤如下: 1)假设有m个备选方案、n个评价准则.首先由决策团队讨论得到方案Ai在准则Cj下的评价值(用概率语言表示),然后利用式(3)—(6)将概率语言术语转化为精确值,并得到如下初始决策矩阵: 2.1.3组合优化赋权 (9) 求解上述模型可得: (10) 利用式(10)即可计算得到组合赋权结果. 基于概率语言的MULTIMOORA排序法的排序步骤为: 5)利用优势理论将比率系统法、参考点法、全乘法得到的排序结果整合为最终的排序结果,该结果即为基于概率语言组合赋权与MULTILMOORA的多准则决策结果. 某仓储型物流企业拟对立体仓库进行智能化升级改造,假设现有4套改造设计方案Uk(k=1,2,3,4)可供选择.该企业首先组织决策团队确定智能仓库设计方案的评价准则(得到7个评价准则),然后拟采用本文方法对备选方案进行评估排序.智能仓库的评价准则及其内涵如表3所示. 表3 智能仓库的评价准则及其内涵 使用本文决策方法的具体过程为: 1)获取决策信息.首先由决策团队讨论得到所有评价准则的序关系(C1>C5>C7>C4>C2>C6>C3), 然后采用概率语言对相邻评价准则进行比较(结果见表4),最后再由决策团队讨论得到每个方案在每个准则上的概率语言评价信息(结果见表5). 表4 相邻准则的重要性评价值 表5 决策团队给出的不同方案的概率语言评价信息 2)转换概率语言评价信息.利用公式(3)—(6)分别将表4和表5的概率语言评价信息转换为精确值,结果如表6和表7所示. 表6 将表4中的概率语言评价值转换为精确值的结果 表7 将表5中各方案的概率语言评价信息转换为精确值的结果 3)确定准则权重.首先根据表6中的数据以及公式(7)—(8)求出各评价准则的主观权重,然后根据表7中的数据以及2.1.2中的公式求得各评价准则的客观权重,最后利用公式(10)求出融合主客观的优化权重.上述计算结果如表8所示. 表8 各准则的权重计算结果 4)确定排序结果.首先利用表7中的评价数据和表8中的组合权重以及2.2中的公式分别求出比率系统法、参考点法、全乘法下的所有备选方案的排序结果,然后根据优势理论将上述3个排序结果进行整合.整合后得到MULTIMOORA排序的最终结果为U2>U1>U3>U4, 如表9所示. 表9 不同排序方法的排序结果 为验证本文方法的有效性和实用性,基于本文案例数据对本文方法、AHP - MULTIMOORA方法[11]、熵权TOPSIS方法[15]进行对比分析. 3.2.1与AHP - MULTIMOORA方法的对比 AHP - MULTIMOORA方法是一种基于单一主观赋权的多准则决策方法.将本文10粒度的概率语言术语集与AHP - MULTIMOORA结合所构建的决策者决策矩阵如表10所示. 表10 AHP决策者决策矩阵 AHP - MULTIMOORA方法的具体计算过程为:首先采用公式(3)—(6)将表10转化为精确值决策矩阵(见表11),然后将该决策矩阵输入到Matlab程序中以计算AHP法下各评价准则的权重值.经计算,各权重值分别为:ω1=0.212 1,ω2=0.115 1,ω3=0.099 2,ω4=0.124 5,ω5=0.183 2,ω6= 0.106 2,ω7=0.159 8.该结果与本文采用G1法求得的结果一致.最后,根据表7和2.2中的公式得AHP - MULTIMOORA方法的各方案最终排序结果与本文方法一致,即均为U2>U1>U3>U4.上述结果表明,本文方法是有效的. 由表10和表4可知, AHP - MULTIMOORA方法对各准则一共进行了49次比较,而本文方法只进行了6次比较,这说明本文决策方法具有更高的决策效率.此外,由于本文方法对客观权重进行了考量,因此本文方法还能够避免单一主观赋权法的主观绝对性. 表11 将AHP决策矩阵中的概率语言转化为精确值的结果 3.2.2与熵权TOPSIS方法的对比 熵权TOPSIS方法是一种经典的基于单一客观赋权法的多准则决策方法.本文参考文献[15]的方法计算本文案例,步骤如下: 表12 标准化决策矩阵 2)采用熵权法计算各评价准则的权重,得ω1=0.213 2,ω2=0.095 3,ω3=0.092 1,ω4=0.114 5,ω5=0.083 6,ω6=0.183 3,ω7=0.217 9.根据该计算结果及表12中的数据即可得加权标准化决策矩阵,如表13所示. 表13 加权标准化决策矩阵 3)根据表13中的数据和TOPSIS法计算设计方案U1—U4到正理想解的相对贴近度,得各方案的相对贴近度分别为: 0.533 8、0.565 6、0.458 8、0.474 7.根据贴近度规则(越接近1方案越优)可得熵权TOPSIS法计算的方案排序为:U2>U1>U4>U3, 该结果与本文方法在U3和U4的排序上存在差异(本文为U2>U1>U3>U4).在表9中, 根据占优理论得MULTIMOORA的最终排序结果为U3>U4.由表12可知,方案U3比方案U4在智能化、安全性、设计成本等3个准则上更具有优势:因此,本文方法比熵权TOPSIS法更加合理. 本文基于概率语言提出了一种改进的MULTIMOORA多准则决策方法,经实验对比表明:该方法比AHP - MULTIMOORA法具有更高的决策效率,且避免决策结果过于主观;比熵权TOPSIS法在赋权问题上更为灵活,且排序结果具有更好的鲁棒性.因此该方法对于解决多准则决策过程中的赋权问题和方案排序问题具有较好的实际应用价值.在今后的研究中,我们将对多准则群决策问题或多准则匹配决策问题进行探讨.
2 指标权重的确定及备选方案的排序
2.1 基于概率语言的主客观组合赋权法


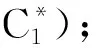

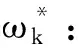
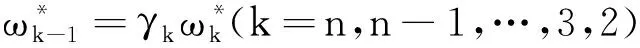

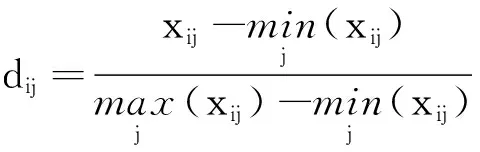


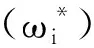
2.2 基于概率语言的MULTIMOORA排序法
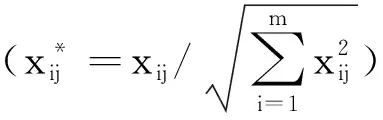
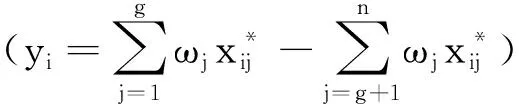
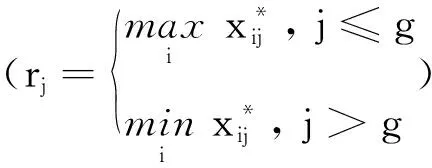
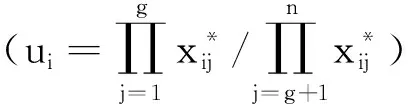
3 算例分析
3.1 算例计算







3.2 对比分析


4 结束语
