基于权重博弈-模糊法的再生路面合理结构研究
2022-09-09叶宏宇周及王选仓
叶宏宇,周及,王选仓
(1.陕西交通控股集团有限公司,陕西 西安 710065;2.陕西高速环境科技有限公司,陕西 西安 710117;3.长安大学 公路学院,陕西 西安 710064)
再生沥青路面性能和使用寿命很大程度取决于其路面结构,不合理结构易导致开裂、坑槽等病害[1-2]。国外较早开展了再生沥青路面结构研究,大致分为经验法和力学-经验法。经验法主要通过建立材料属性、结构、破坏类型等的经验式,确定结构厚度,如CBR法和AASHTO法[3]。力学-经验法采用圆形均布荷载计算弹性层状体系路面结构的应力应变,认为结构破坏形式为永久变形及疲劳开裂[4]。再生路面结构设计参考沥青路面设计方法,AASHTO[4]提出再生料结构层系数通过查表或永久变形、应变和疲劳性能计算得到。AI[5-6]对再生结构提出了两种方法,计算法与图表法。我国对于再生路面结构也进行了相关研究,戴俊搴[1]基于灰色关联度分析再生路面荷载应力,提出路面结构及材料优化设计方法。许严[7]计算再生料与新料之间等效结构厚度系数,给出基于性能特点的再生结构设计思路与流程。曾梦澜[8]提出冷再生结构设计原则,并给出常用材料及厚度设计图。交通运输部2019年颁布实施的《公路沥青路面再生技术规范》也提出了冷热再生路面结构设计方法与结构组合。
新疆地区再生路面应用较晚,参照的设计规范偏向于原则性规定,低温设计温度取值与公路服役年限不匹配,由于气候、施工等与其他地区有较大差异,规范推荐及其他地区采用的再生结构不完全适合于新疆地区。基于此,本文拟定九种再生路面结构,分析动力学响应;建立Gumbel极值模型,提出基于重现期的低温设防指标;基于全寿命周期费用模型评价再生结构经济性;最终建立权重博弈-模糊法模型评价再生路面结构综合性能,提出新疆地区再生路面合理结构,为新疆地区再生路面结构设计提供参考。
1 再生沥青路面结构及设计指标确定
结合我国再生沥青路面结构及新疆地区气候条件,拟定路面结构方案如图1。其中,A-1、A-2、A-3为双层或三层面层+再生层+水稳碎石基层,A-4改变水稳碎石基层厚度,A-5改变面层厚度;B-1~B-2为三层面层+热再生基层+级配碎石结构;C-1~C-2采用面层+水稳基层对比。
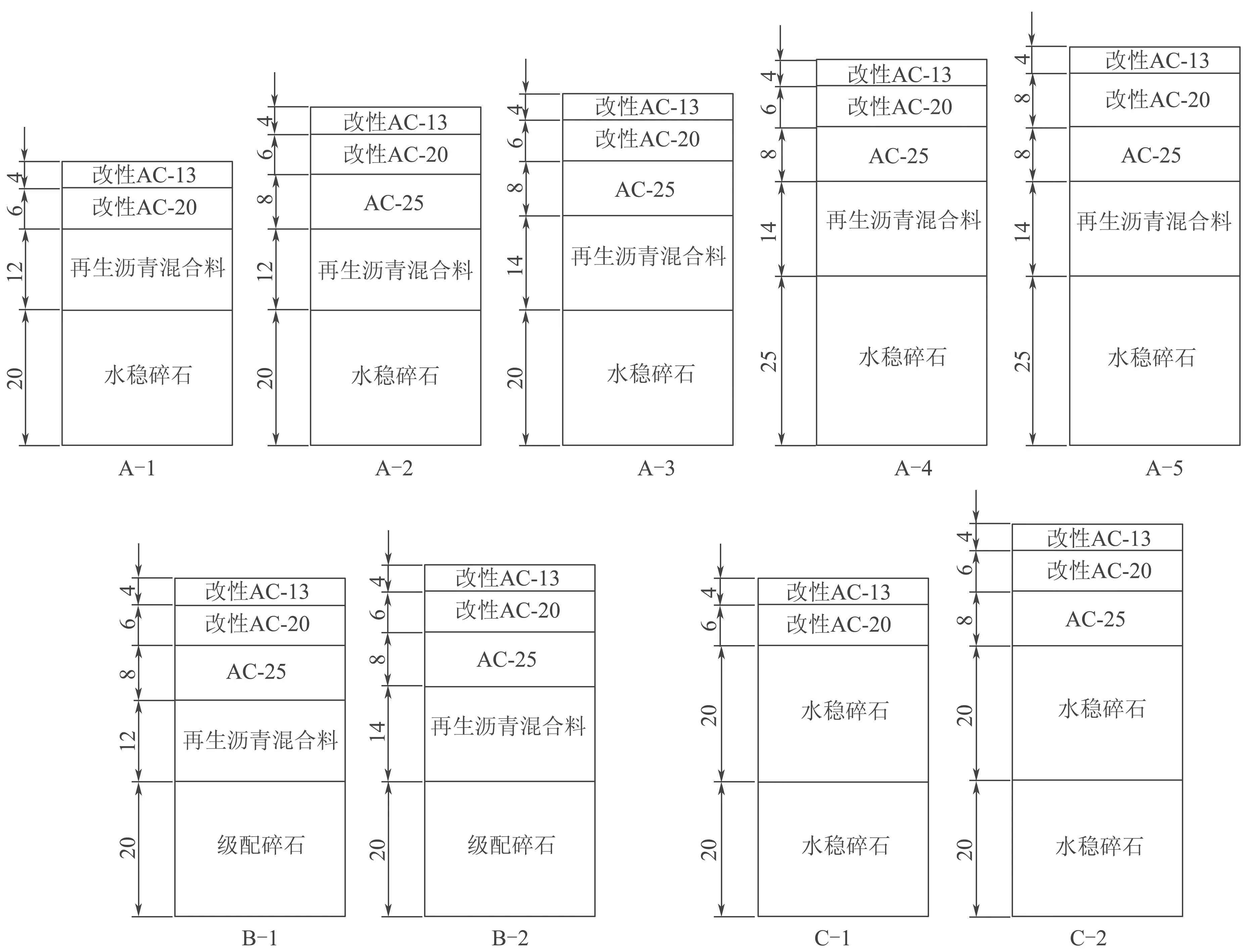
图1 路面结构方案
根据我国再生路面设计规范及国外SHELL法、比利时法、NITRR法及美国联邦公路局法路面结构设计指标的规定[9],拟定力学指标为沥青层底拉应变、再生层底拉应变、半刚性层底拉应力、铣刨后旧路顶面压应变。
2 再生路面结构力学响应分析
2.1 力学计算模型及参数
(1)路面结构参数选取。模拟实际路面受力,采用动态荷载与动态模量分析路面结构力学响应[10],参数取值如表1,土基阻尼系数取0.5,其余取0.05。
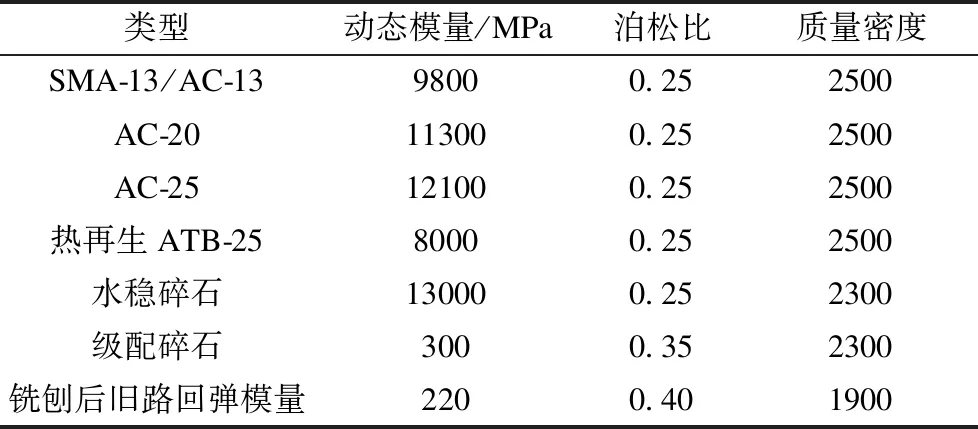
表1 路面结构层计算参数
(2)荷载作用参数选取。取100、120、160、180 kN的双圆垂直均布荷载,计算轮压及荷载等效矩形[11],结果见表2。
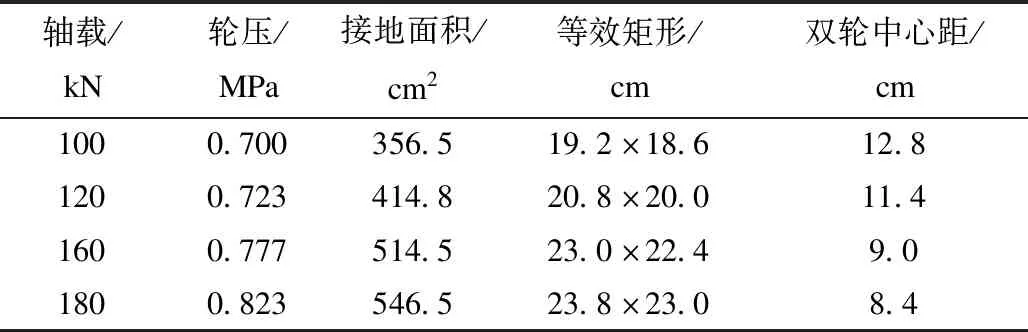
表2 轴载等效计算结果
(3)有限元模型建立。假定路面结构为多层连续弹性体系,层间接触完全连续,选用C3D8R单元,假定底面完全约束,横向与X轴平行断面无Y方向位移,纵向与Y轴垂直断面无X方向位移[10-11]。为方便计算,车速取108 km/h,即0.1 s内占有18个网格。网格划分整体0.3,荷载作用区域0.1,如图2所示。

图2 路面结构力学计算模型
2.2 再生路面结构力学响应分析
通过ABAQUS建立不同路面结构力学模型,计算荷载100、120、160、180 kN和铣刨后旧路回弹模量60、120、180、240 MPa下结构的力学响应。其中,计算不同轴载作用再生路面结构动力学响应时,旧路回弹模量取220 MPa;计算不同旧路回弹模量结构力学响应时,轴载取100 kN。结果如图3~图6所示。
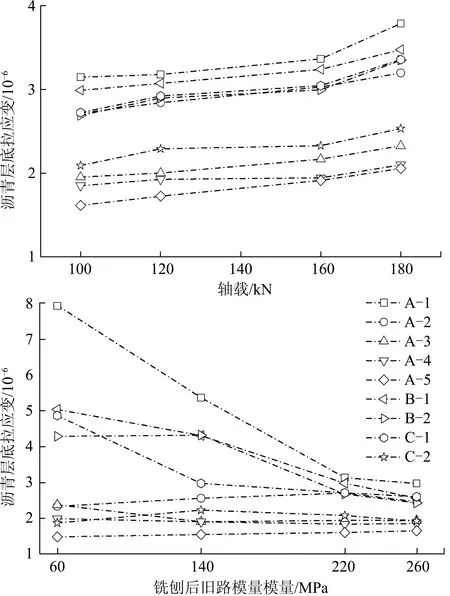
图3 沥青层底拉应变规律
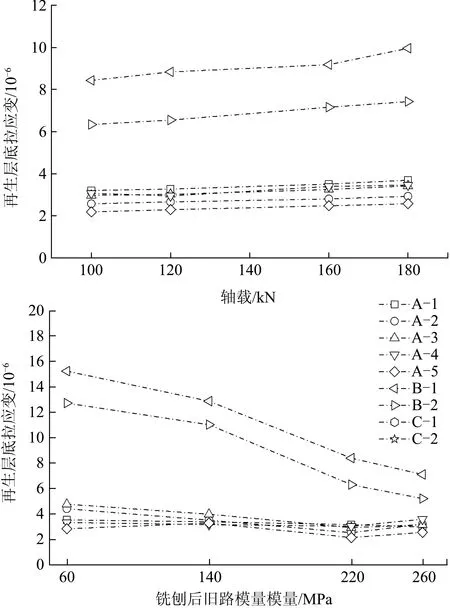
图4 再生层底拉应变规律
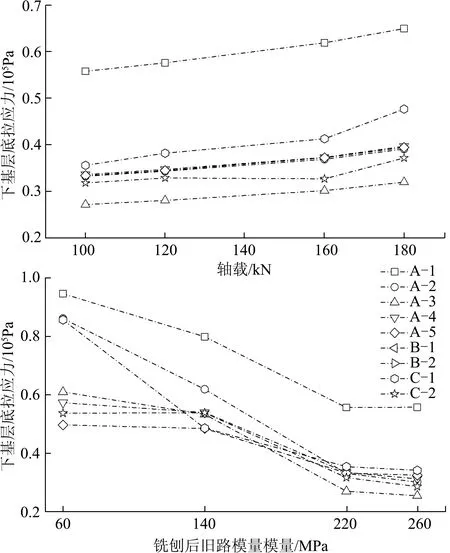
图5 下基层层底拉应力变化规律
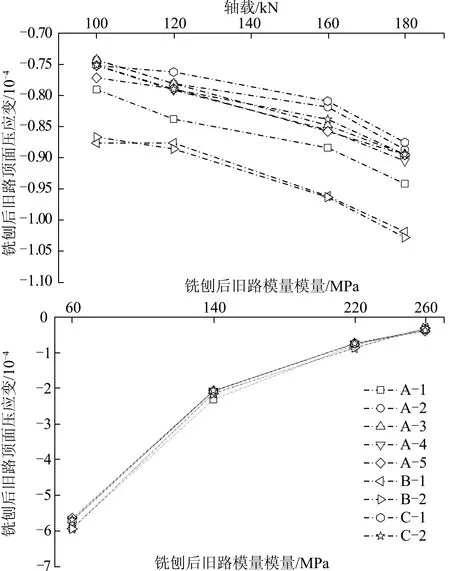
图6 铣刨后旧路顶面压应变变化规律
由图可得:
(1)沥青层底拉应变与轴载正相关,与铣刨后路基模量负相关,受再生层厚度影响显著,受下面层厚度及半刚性层厚度影响不显著。标准轴载下不同方案沥青层底拉应变排序为:A-1>B-1>C-1>A-2>B-2>C-2>A-3>A-4>A-5。
(2)再生层底拉应变规律与沥青面层层底拉应变相近,面层及水稳基层厚度增加均会减小再生层底拉应变;随再生层厚度增加,柔性层结构再生层底拉应变降低,半刚性结构再生层底拉应变增大;柔性基层结构受旧路模量影响最大。标准轴载下不同方案再生层底拉应变排序为:B-1>B-2>A-1>A-4>A-3>A-2>A-5。
(3)下基层底拉应力与轴载正相关,与铣刨后旧路模量负相关;不同结构敏感性不同,面层厚度越小,拉应力对旧路模量敏感性越大;基层厚度对层底拉应力影响较小。标准轴载下不同方案基层层底拉应力排序为:A-1>C-1>A-4>A-5>A-2>C-2>A-3。
(4)铣刨后旧路顶面压应变与轴载正相关,与土基模量负相关。旧路模量越大,厚度对压应变影响越小,各方案的旧路顶面压应变结果相差不大,排序为:B-1>B-2>A-1>A-5>A-4>C-1>C-2>A-2>A-3。
3 基于重现期的低温设防值及开裂预估
3.1 低温重现期
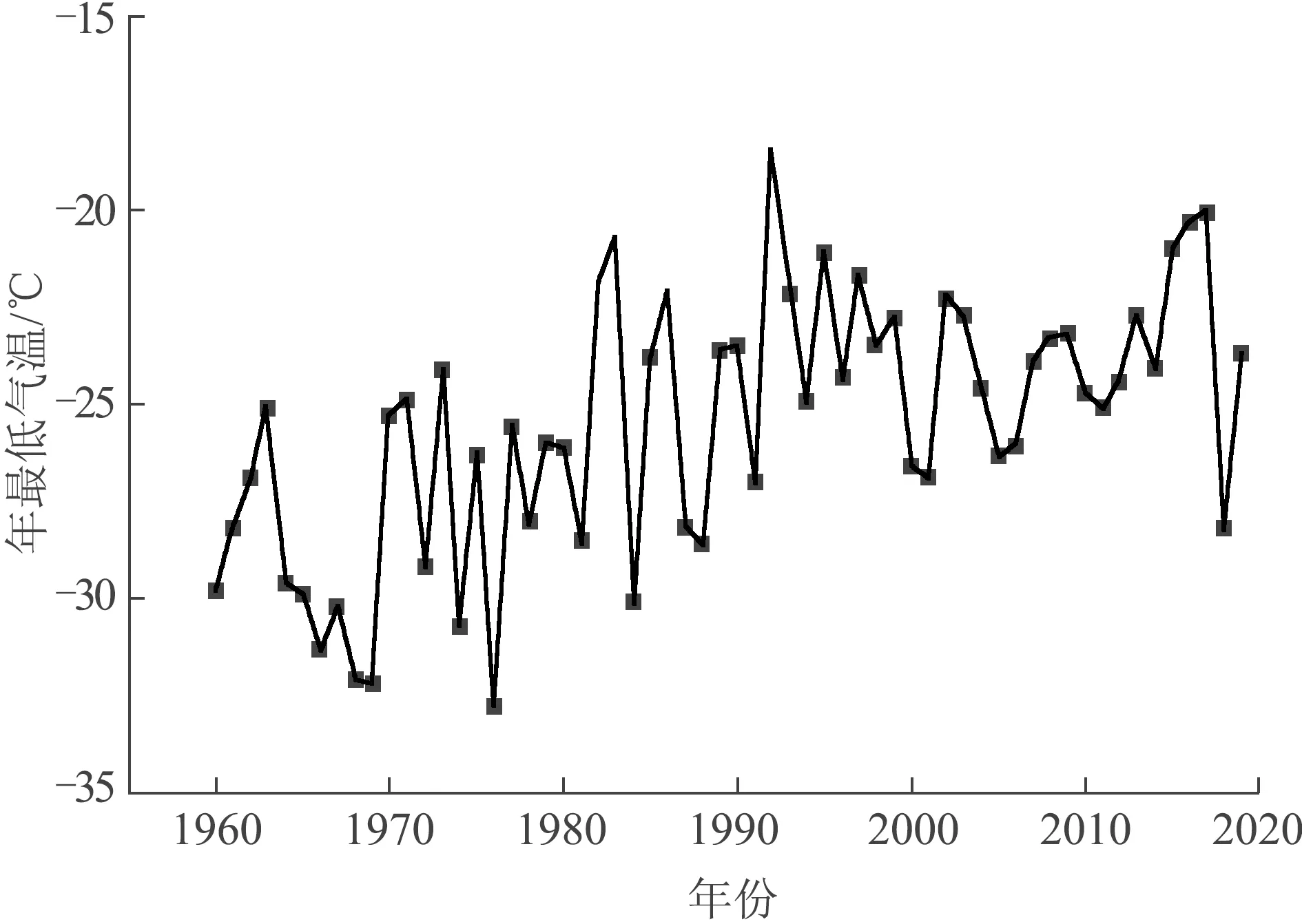
调查得,新疆地区道路受低温开裂影响严重[12],而设计规范中低温设计温度取连续10年最低平均气温与公路设计年限不匹配。因此,引入低温重现期,提出基于重现期的道路低温设计指标及模型。重现期T是指研究对象如降雨等在某一周期内出现的平均概率,计算如式(1)。以桥梁洪水再现频率为例,T100指每100年内最可能出现的洪水流量极值,其倒数即为该值出现概率。道路设计时,低温设计温度同样需预测一定重现期内最可能出现的极值。
T(x≥xp)=1/P(x≥xp)
(1)
式中:xp—拟定的极值,P—该值出现概率,T—该值出现的重现期。
3.2 基于重现期的低温指标计算
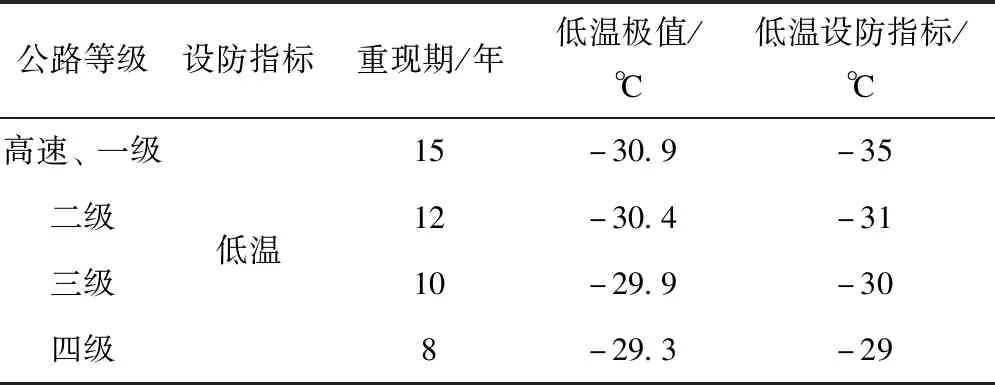
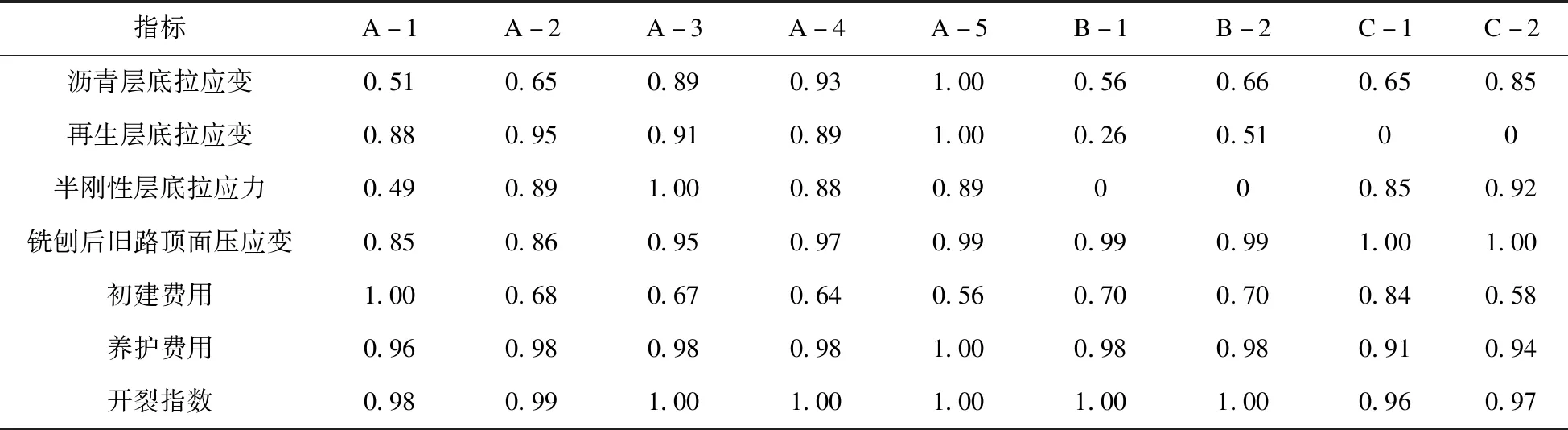
为得到重现期内极值,常采用皮尔逊Ⅲ型曲线和Gumbel曲线极值模型分析对象在过去某周期变化规律,预测将来可能出现概率及数值。Gumbel曲线极值模型在气温、降雨等应用广泛且结果可靠。气温变化符合正态分布[13],采用矩法预估建立Gumbel曲线函数如式(2)。重现期如式3,将C=-ln[ln(T-1)-lnT]代入式(3),解得式(4),计算样本均值和标准差,即可得重现期内极值如式5。当确定重现期后,根据气象站实测数据,计算均值方差,代入式(5)得极限低温设防值。
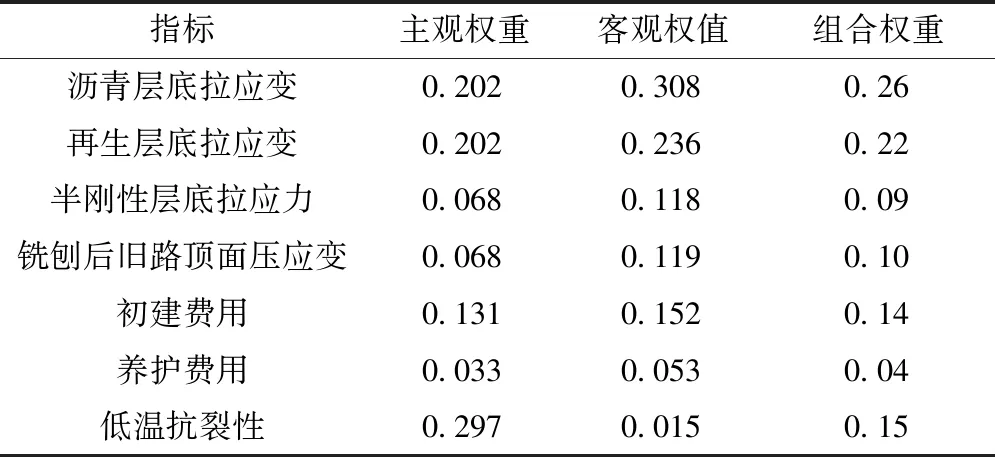
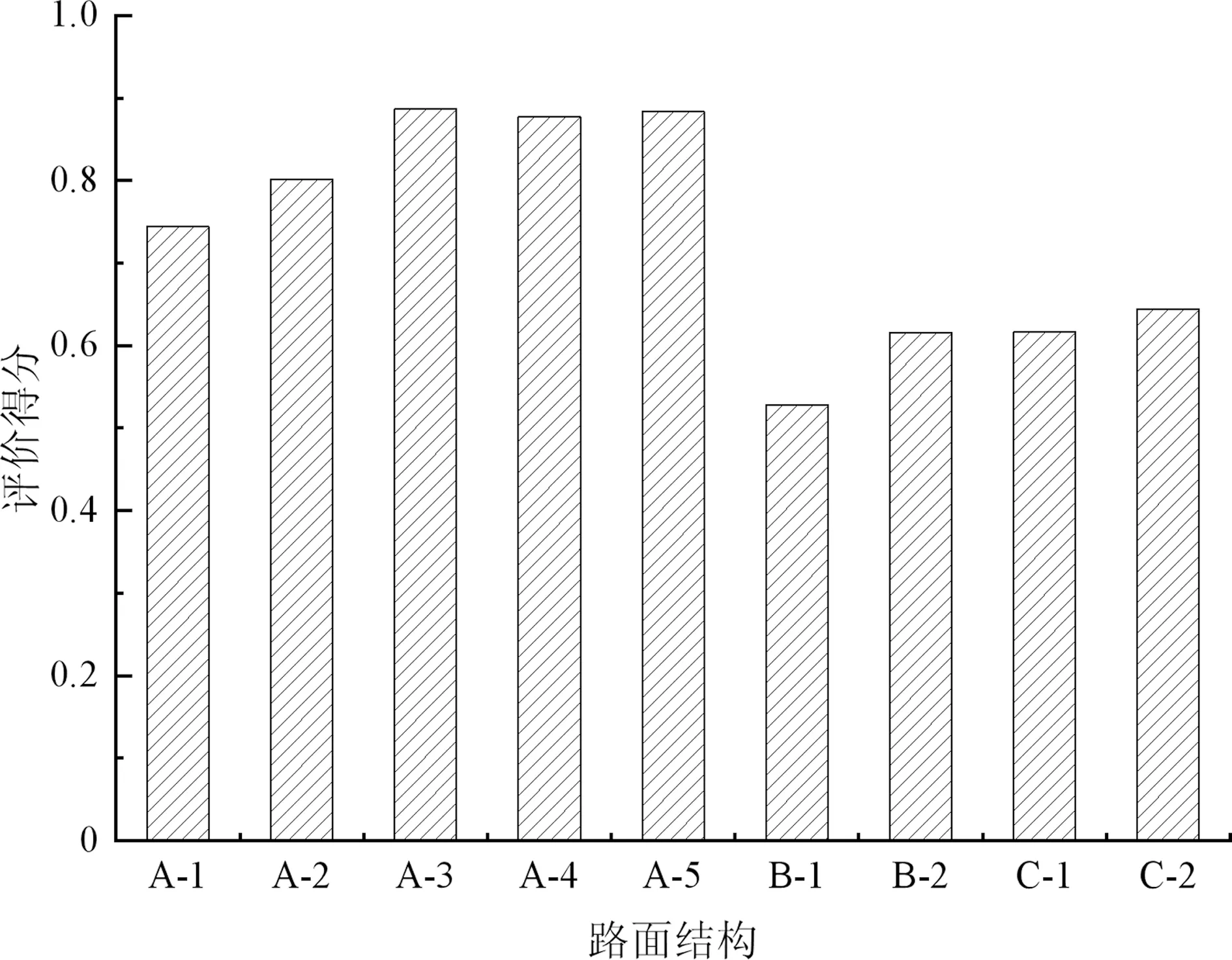
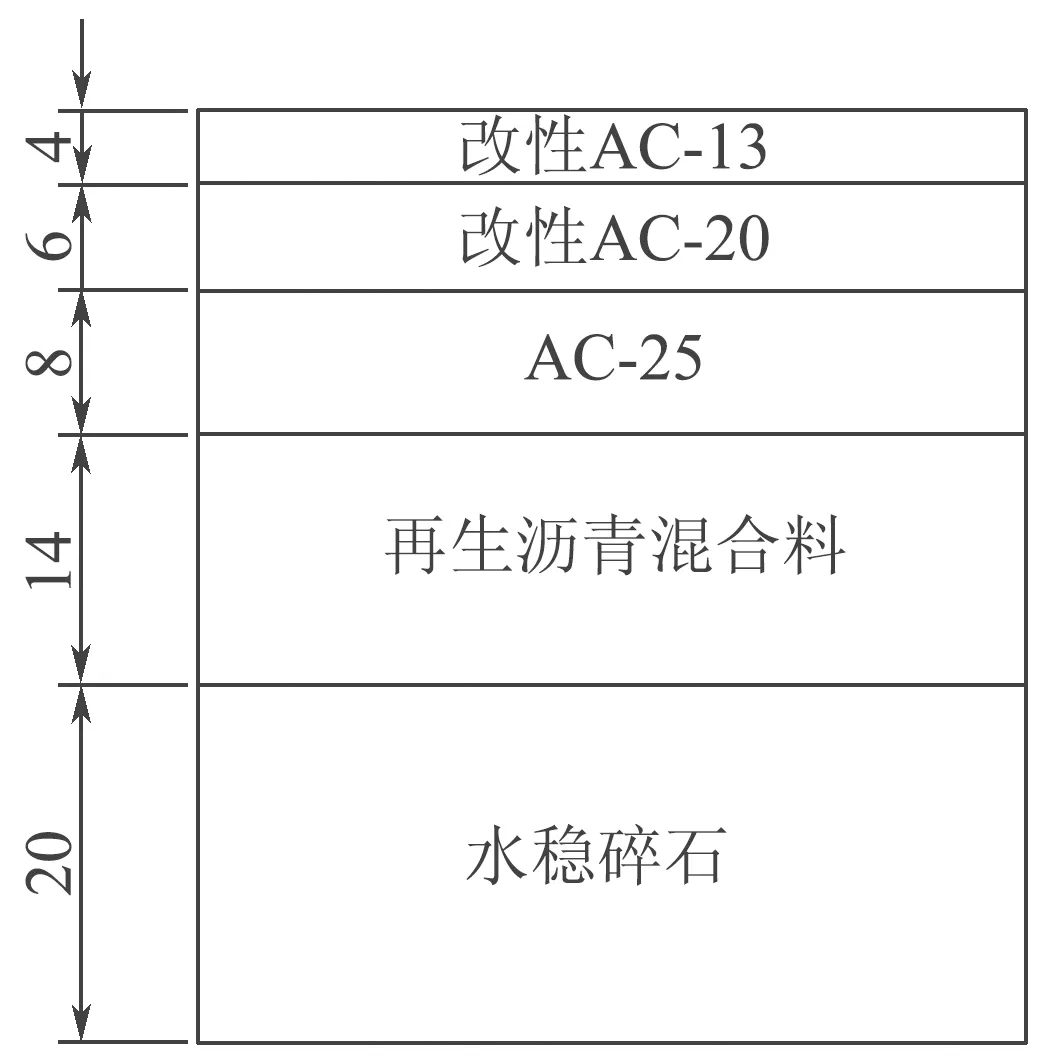
F(x)=P(x (2) (3) x=μ+C·δ (4) (5) 式中:φ—Gumbel曲线的离均系数,是P(x)的函数, 样本均值,σx—标准差,Cv—变异系数。 图7 1960—2019年乌鲁木齐年最低气温 表3 低温设防值 参考沥青路面设计规范低温抗裂公式,采用基于重现期的低温设防值代替连续10年年最低气温均值,见式(6)。以乌鲁木齐为代表,预估各路面结构低温抗裂性见表4。 表4 面层开裂指数结果 CI=1.95×10-3Stlgb-0.075(Tt+0.07ha)lgSt+0.15 (6) 式中:CI—低温开裂指数;ha—沥青层厚(cm);b—路基参数,取5;St—沥青劲度,取50 MPa;Tt—低温设防指标,按表3取值。 再生路面全寿命周期指从开始再生到报废停止服役,费用由初建、养护维修、用户费用及路面残值组成[14],用户费用受结构影响小,分析期长,数值难以预估,因此不作考虑。养护维修费用主要用于裂缝处治,按年等额支付,根据造价资料单价取15元/m。路面残值取初始投资的50%,折现率7%,费用计算如式(7)~(10),结果如表5。可以看出,全半刚性基层结构费用最高。 表5 费用分析(百元/米) (7) NCXZ=PW×NC (8) (9) (10) 通过结构力学指标、低温性能、经济性分析得,采用单因素分析得到的结构性能排序不同,不能明确判断其优劣程度[15-16]。因此,建立权重博弈-模糊法模型评价路面结构综合性能,步骤如下。 (1)建立路面结构目标集: U={u1,u2,u3,…,un} (11) 式中:ui(i=1,2,3,…,n)是目标路面结构。本文目标集为拟定的九种路面结构。 (2)建立结构评价影响因素集: V={v1,v2,v3,…,vn} (12) 式中:vi(i=1,2,3,…,n)是再生路面结构影响因素。 针对路面结构进行单因素评价时,某一影响因素评价集为: R={r1,r2,r3,…,rm} (13) (3)建立影响因素隶属度关系矩阵:对不同影响因素评价结果建立集合得到隶属度矩阵。 (14) 选取铣刨后旧路模量220 MPa、荷载100 kN的力学指标,低温开裂指数,初建费用、养护费用建立路面综合评价体系。根据式(11)~(14),构建隶属度矩阵如表6所示。 表6 隶属度矩阵 (4)基于组合权重-博弈论进行赋权。AHP-熵值法法考虑了主客观权重,但在均衡赋权上存在不足。因此,引入博弈论优化AHP-熵值法,步骤如下: ①构造综合权重集: (15) 式中:ak>0,为权重系数;T=[t1,t2,…,tn]为m种方法确定的权重集权重综合向量。 (16) ③求[a1,a2,…,am]T,归一化处理得基于博弈论的组合权重: (17) 本文m=2,W=[w1,w2,...,wn]为AHP法确定的主观权重,V=[v1,v2,...,vn]为熵值法确定的客观权重,代入式(16),求得权重系数a1=0.5376,a2=0.6005,归一化处理得a1*=0.472,a2*=0.528,代入式(17)得基于博弈论确定的组合权重如表7所示。 表7 再生沥青路面结构各指标权重 (5)确定综合评价模型。综合评价模型如式18。将表6、7带入式(18),得不同再生路面结构综合评价指数见图8。可得,全柔性基层结构综合性能最差,评分0.6以下;全半刚性基层结构力学性能高,但经济性差,综合评分0.6~0.7;再生层+半刚性基层结构性能最优。结构综合排序为:A-3>A-5>A-4>A-2>A-1>C-2>C-1>B-2>B-1。推荐新疆地区再生沥青路面合理结构见图9。 图8 不同路面结构综合评价结果 图9 新疆地区再生路面合理结构(单位:cm) B=t*×R (18) (1)本研究拟定九种路面结构,采用有限元分析再生路面结构在不同荷载及旧路模量下的动力学响应。结果表明,不同路面结构对轴载、铣刨后旧路模量的敏感性不同,路面结构力学指标受铣刨后旧路模量影响较大,旧路模量从140 MPa增大到220 MPa时变化幅度最大;沥青层厚度对沥青层底拉应变影响显著,水稳基层层底拉应力受再生层厚度影响显著,各方案的旧路顶面压应变结果相差不大。 (2)建立Gumbel极值模型,提出了基于温度重现期的低温设防指标及计算方法,以乌鲁木齐为代表,确定了高速、一级公路低温设防值为-35℃,二、三、四级公路分别为-31℃、-30℃、-29℃。改进低温抗裂公式,预估了不同再生路面结构低温抗裂性。 (3)建立再生路面结构全寿命周期费用模型,得到了不同再生路面结构全寿命周期费用排序,三层面层+水稳碎石基层+水稳碎石底基层总费用最高,其次为三层面层+再生基层+水稳底基层,双层面层+再生层+水稳底基层费用最低。 (4)建立权重博弈-模糊法路面结构综合评价模型,得到了不同路面结构综合性能排序,推荐新疆地区再生路面合理结构为:4 cm改性AC-13+6 cm改性AC-20+8 cm AC-25+14 cm再生层+20 cm水稳碎石。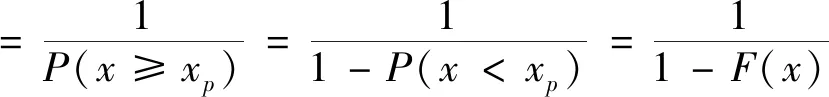
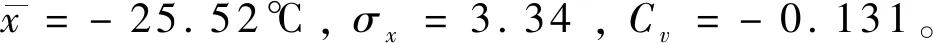
3.3 基于重现期的再生路面结构低温开裂预估

4 基于全寿命周期的再生路面结构经济性分析

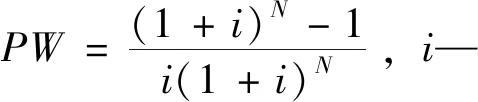
5 基于权重博弈-模糊法的再生路面合理结构研究
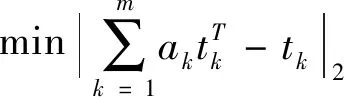

6 结论
