2022年浙江省数学高考第22题探析
2022-09-09虞哲骏
虞哲骏, 冯 斌
(1.宁波市镇海中学,浙江 宁波 315200;2.宁波市教育局教研室,浙江 宁波 315100)
“本手、妙手、俗手”是围棋的3个术语.对于数学而言,笔者认为“本手”是基础知识与通性通法,“妙手”是灵感乍现的“秒杀”与“创造”,“俗手”是死记硬背的“模型”和“套路”.数学教学应该立足“本手”,只有“本手”的功夫扎实了,理解深刻了,数学能力水平与素养才会提高,才有可能出现“妙手”.在高三复习中,我们有大量的题目要做要讲,但笔者认为真正要用好的题目是高考真题.挖掘高考真题的本质内涵才是正道,才能引导学生从“本手”走向“妙手”.自2004年起,浙江省数学高考自主命题形成了自己的特点和风格,它始终遵循有利于学生、有利于高中数学教学、有利于高校选拔人才的原则,在坚持考查基础知识的同时,注重考查思维能力[1].2022年是浙江省自主命题的最后一年,下面笔者从2022年浙江省数学高考第22题入手,分析第2)小题第②问的3种解法,尝试从本质上探究该题的背景,以期为平时的复习和教学提供参考.
1 真题呈现

1)求f(x)的单调区间.
2)已知a,b∈R,曲线y=f(x)上不同的3个点(x1,f(x1)),(x2,f(x2)),(x3,f(x3))处的切线都经过点(a,b).证明:

②若0 (注:e=2.718 28……是自然对数的底数.) (2022年浙江省数学高考试题第22题) 该题结构简洁、精炼,但所蕴涵的思想却很丰富,求解难度也极大.主要考查导数在求解函数切线方程、判断函数的单调性以及函数与不等式的综合问题中的应用,意在考查学生的数学运算能力、化归与转化的思想,贯穿了数学运算和逻辑推理的核心素养. 第1)小题难度不大,主要考查函数的单调区间,此处不再讨论.第2)小题的第①问主要考查切线方程,从方程有3个不同的解的角度入手,证明不等式,难度适中.第②问看上去结构比较复杂,涉及的变量较多,主要考查零点范围估计问题,难度较大.以下笔者将从减元的视角出发,介绍第②问的3种解法. 分析由x1,x2,x3满足y=f′(xi)(x-xi)+f(xi),知x1,x2,x3是f′(x)(x-a)-f(x)+b=0的3个正实数根,即 因为a 0 于是 上式等价于 由g(t1)=g(t3)=0,得 且 t1>t3, 即 从而φ(x)在(1,+∞)上单调递增,于是 可知h(x)在(0,1)上单调递增,故h(x) 两式相减,得 化简得 要证 只需证 故只需证 从而 (1) 分析y=g(t)的图像可知:对于给定的m∈(0,1),当b增大时,g(t)图像下移,t1,t3均减小;反之当b减小时,g(t)图像上移,t1,t3均增大. 从而φ(x)在(0,+∞)上单调递增.又φ(0)=0,故引理得证. m(t1-1)2=2(t1-1-lnt1), 由引理1可知 解得 从而 再证明式(1)的左边:只需证明极端情况,此时 只需证 由引理1可知 1)当0 2)当x>1时, 解法3是本题的“妙手”,可遇不可求.要想下出真正的“妙手”,必须在平日有一定的经验积累和反思总结,形成较为完善的知识体系,唯有这样,才有可能完成真正卓越的“妙手”. “问渠哪得清如许,为有源头活水来”.原题源于何处,翻翻我们学的教材、做做历年高考真题就知道了.事实上,教材和历年高考真题是高考试题的重要来源,是数学知识的“生长地”,是高考复习的“根据地”,是高考试题的“策源地”.笔者查阅了相关资料,发现本题和2014年全国数学高考Ⅱ卷理科第21题有异曲同工之妙. 例2已知函数f(x)=ex-e-x-2x. 1)讨论f(x)的单调性; 2)设g(x)=f(2x)-4bf(x),当x>0时,g(x)>0,求b的最大值; (2014年全国数学高考Ⅱ卷理科试题第21题) 在例1第②问的证明过程中,涉及对lnx的有理形式的刻画,因为函数f(x)=lnx在x=0处无意义,所以转而研究g(x)=ln(x+1)的性质.在高等数学中,我们经常会借助泰勒展开,得到麦克劳林公式 经计算可得: 1)当λ≤0时,恒有 即 即 令a=x2,b=1,则 (2) 可以看出不等式结构变得比较复杂了,因此我们的讨论停留于此. 即 则 2λ2-4λm(m+2)+m(3m2+4m-1)≥0. 令φ(m)=2λ2-4λm(m+2)+m(3m2+4m-1),则 φ′(m)=(m+1)(9m-8λ-1). φ′(m)=(m+1)(9m-8λ-1)<0, 至此,我们完成了命题意图的深度挖掘. 高考以“基础性、综合性、应用性、创新性”为考查要求,评价学生素养的达成程度[3].例1作为2022年浙江省数学高考试题的压轴题,以高中数学常见的函数为素材,以常用的方法为手段构造函数,并利用这些函数的性质和特点进一步研究问题.将函数、导数、不等式等知识有机结合,考查学生灵活应用知识解决复杂问题的能力,对逻辑推理能力、运算能力有较高的要求,有效区分考生的思维层次,为高校选拔优秀人才服务.纵观历年高考压轴题,从来不是偏深的难题、怪题,而是体现触类旁通的灵活性和变通性.基于高考的教学导向,我们在平时的解题教学中也要更新理念,努力寻求合理的教学策略,即夯实双基,引导思考,培养能力,提升素养.2 解法探究

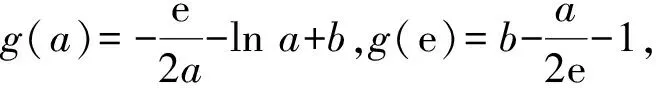

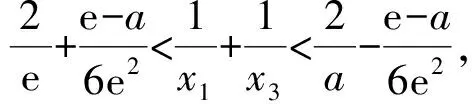
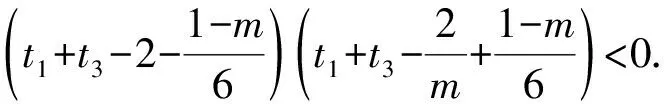





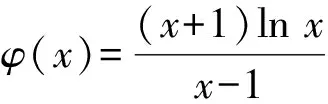



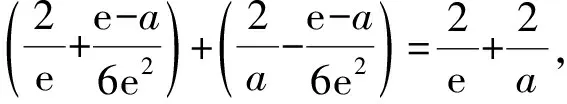

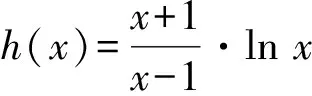




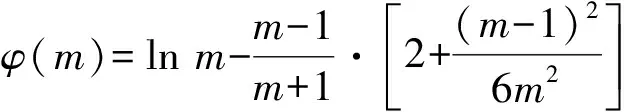
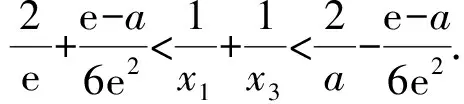


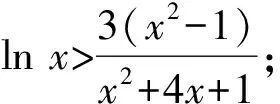
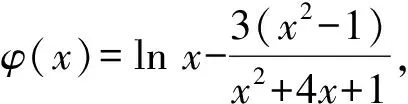

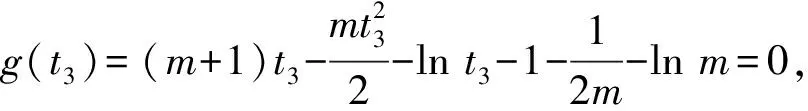


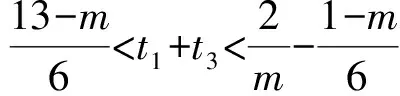
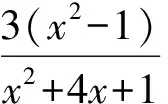
3 试题探源

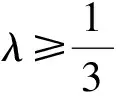

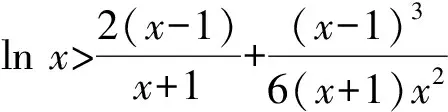
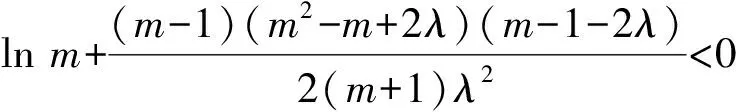
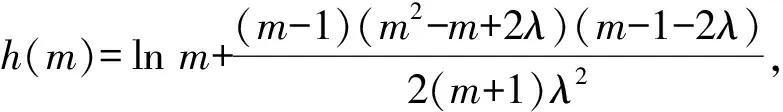

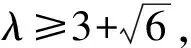
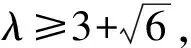
4 教学启示
