科学分析学情 精准把握教学
——一节二次函数习题课的教学设计、实施与思考
2022-09-09钟珍玖
钟珍玖
(江阴市第一初级中学,江苏 江阴 214400)
1 学情分析
学情分析是教学设计和教学设施的重要环节,是课堂教学中落实学生为主体的基础和保障.在教学设计时分析学情可以精选教学内容,确定教学方法,在课堂教学中根据学情决定教学的方向和进程,使教学内容更具有针对性,使教学策略更符合学生的认知水平,真正实现“以学定教”.学情分析应该针对学生的学习态度、学习心理、思维方法进行,找准教学的起点和增长点.
1.1 知识技能基础
本节课学生应掌握的知识基础为二次函数的性质,特别是要求学生熟练掌握“已知一个变量的值,求另一个变量”或“设定参数,用参量表示点的坐标和线段的长度”,并且会求二次函数的最值.另外用待定系数法求二次函数的解析式也是本节课的重要知识基础,要构造二次函数模型解决问题,必须熟练建立函数模型,才能为问题的顺利解决奠定基础.
1.2 问题解决方法
本节课的重点内容是在直角坐标系中求三角形的面积,具有代表性和典型性.在初中阶段,解决此类面积问题的策略是“化斜为正”,也就是把三角形的底和高转化成与x轴、y轴平行(重合),方法就是把三角形“割、补”或者作平行线进行等积变换求三角形面积.学生在学习一次函数和反比例函数时,对于割补法求图形的面积有一定的基础,但是还不够熟练,作平行线构造等积三角形要求较高,需要强化训练.
1.3 数学思想观念
二次函数中求三角形面积问题,典型的数学思想就是“数形结合”,先设点的坐标,再用点的坐标表示线段长度,进而求三角形面积,也就是用代数方法解决几何问题,其中还蕴涵着函数思想和方程思想.九年级学生对数学思想方法有了一定的理解,但还没有达到应用自如的程度.
2 问题设计与教学实施
习题课的课堂问题设置应满足基础性、关联性、生成性、思想性,只有这样的问题才能保障课堂教学的有效性,而这些问题的设计和实施都要依赖于学情,符合当前学生的认知规律.
问题1如图1,在平面直角坐标系中,抛物线与x轴交于点A,B,其中点B的坐标为(3,0),顶点P的坐标为(1,2),求此抛物线的函数表达式.

图1
基于学情的教学设计与实施:学生在学习了二次函数性质的基础上,运用二次函数模型解决问题,最为重要的知识基础就是求二次函数解析式,确定二次函数模型.设计问题1是让学生熟练运用待定系数法求二次函数的解析式,可以用顶点式方程设y=a(x-1)2+2,代入点B的坐标,或者根据对称性求出A(-1,0),用交点式方程设y=a(x+1)(x-3),代入点P的坐标即可求出函数表达式.这样的设计是因为有部分学生用交点式方程求二次函数表达式还不够熟练,缺乏数形结合的意识,同时也体现了基础性和关联性.
问题2在问题1的基础上设此抛物线与y轴交于点C,求出以A,B,C,P中3个点为顶点的三角形面积.
基于学情的教学设计与实施:面积问题是各级各类考试的重要考点,把三角形补成矩形求三角形面积,学生对此方法比较熟悉,用分割法求三角形面积需要强化.在4个点构成的4个三角形中,△ACP与△BCP的面积需要用割补法来求.以求△BCP的面积为例,学生的解法如下:
方法1如图2,过点P作PE∥x轴交y轴于点E,过点B作BD∥y轴交PE于点D,则
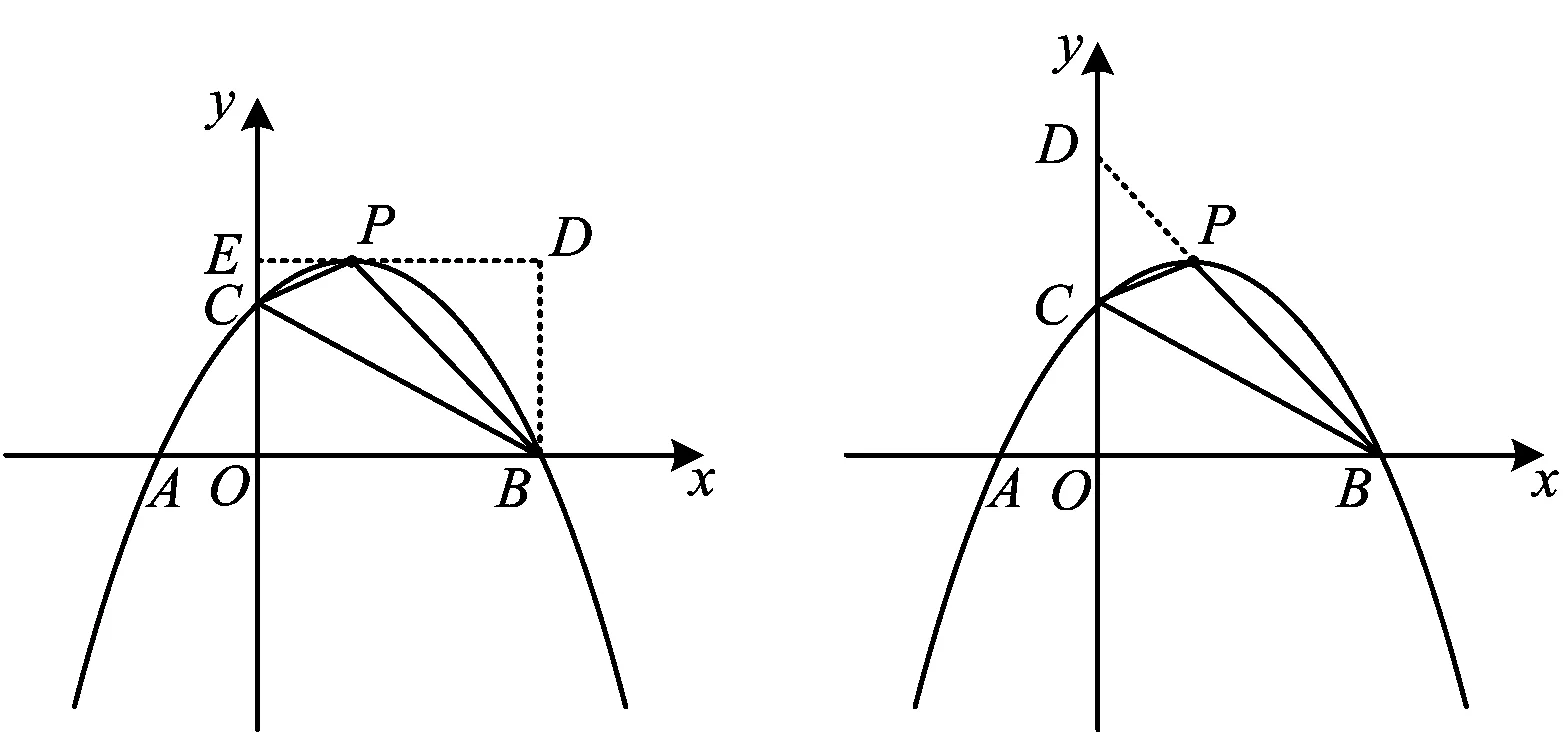
图2 图3
S△BCP=S矩形EOBD-S△OBC-S△ECP-S△BDP.
方法2如图3,延长BP交y轴于点D,则
S△BCP=S△BCD-S△CDP.
方法3如图4,联结OP,则
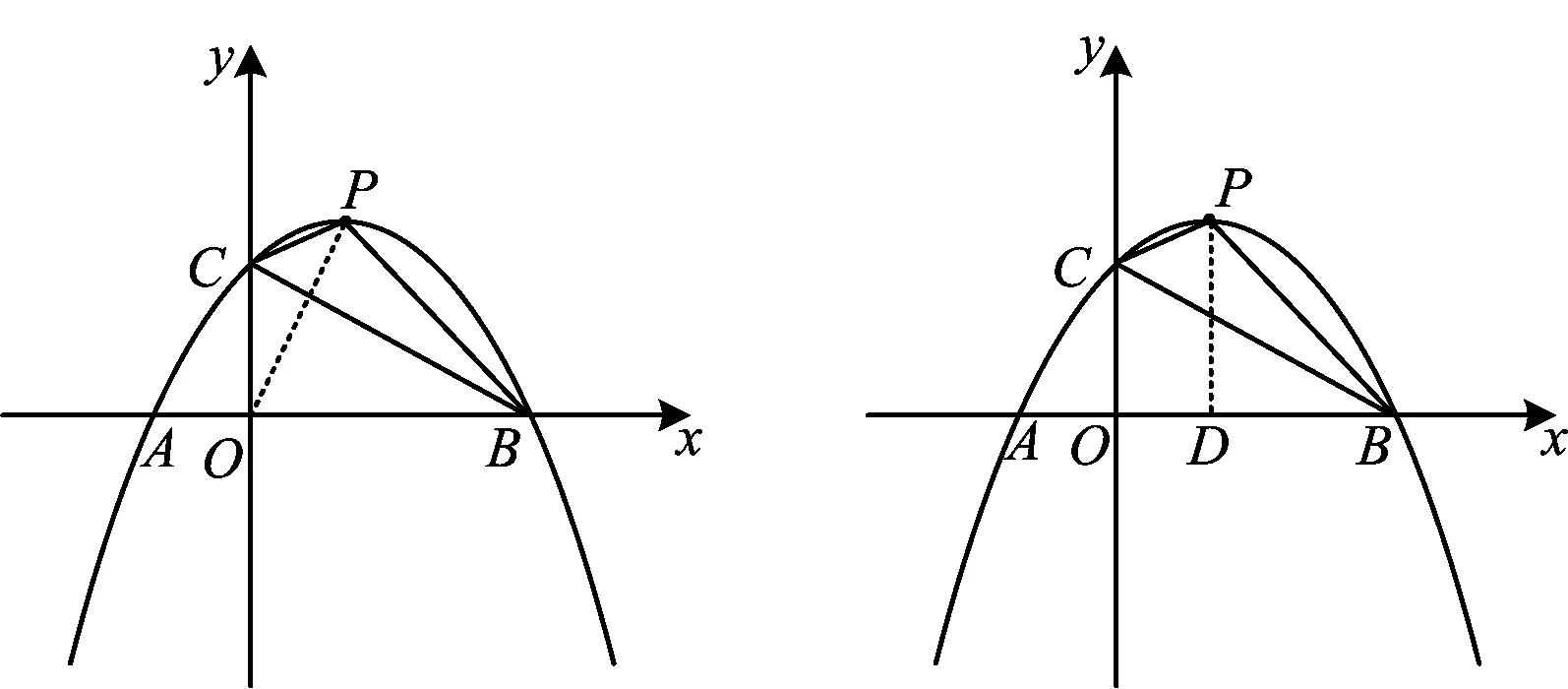
图4 图5
S△BCP=S△OCP+S△OBP-S△OBC.
方法4如图5,过点P作PD⊥x轴于点D,则
S△BCP=S梯形OCPD+S△BDP-S△OBC.
这4种方法都是学生比较熟悉的割补法求坐标系中三角形的面积,其中方法3要求较高,实际上是割补法的融合.在学生得出这些方法后,教师鼓励学生归纳这些方法的共同特点为“化斜为正”,即通过割补法把三角形面积转化成底和高在坐标轴上或者和坐标轴平行的直线上,利用点的坐标求线段长度,从而求出三角形的面积.
方法5如图6,过点P作PD∥y轴交BC于点D,则

图6 图7
方法6如图7,过点P作DE∥BC分别交x轴、y轴于点E,D,△BCP与△BCD同底等高,则S△BCP=S△BCD(或者S△BCP=S△BCE).
根据教学过程的学情看,前面4种方法大多数学生都能较好地掌握,方法5和方法6是本节课的重点和难点,特别是方法6能够独立思考出此种方法的学生非常少.在讲解了这种方法后,让学生再思考构造与△BCP面积相等的三角形,能够解决问题的学生仍然不多,实际上作三角形3条边的平行线构造与△BCP面积相等的三角形都是可行的.问题2的设计有承前启后的作用,是本节课的重点内容,也是渗透思维方法和解决问题策略的关键所在.
问题3如图8,若点D是直线BC上方抛物线上的动点,求△BCD面积的最大值,并求此时点D的坐标.
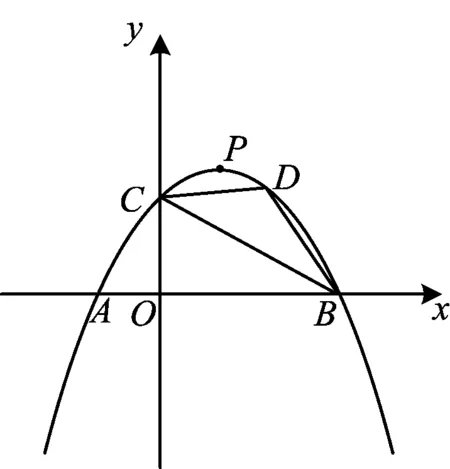
图8
基于学情的教学设计与实施:问题3中的点D为动点,即把问题2一般化,△BCD的面积虽然随着点D的位置变化而变化,但是求解面积的方法仍然和问题2一致,可以让学生巩固割补法和构造法求三角形的面积.解决问题的方法虽然不变,但设点D的坐标,把三角形的面积用引入的变量来表示,体现了函数的思想,深化了学生对函数思想的理解,学会用代数手段来刻画运动变化的问题.这样的设计是把学生难以掌握的数学思想方法渗透在平时的教学中,加强教学的针对性,为提高思维能力打下坚实的基础.
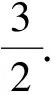
基于学情的教学设计与实施:问题2中求面积的方法在问题4中仍然是适用的,让学生再次熟悉在平面直角坐标系中用“化斜为正”的方法求三角形的面积.问题4的设计是问题2和问题3的延续,由一般化情形再回到特殊情况,即三角形的面积为特殊值,就是变化中的确定.用方程模型来刻画和解决问题,体现了方程的思想.
3 教后思考
3.1 聚焦学情分析
奥苏伯尔在其名著《教育心理学》的扉页中写道:“如果我不得不将教育心理学还原为一条原理的话,我将会说,影响学习的最重要的因素是学生已经知道了什么,我们应当根据学生原有的知识状况去进行教学.”可见学情分析对于教学设计与实施的重要性.从中学数学教师教学的实际来看,对于学情分析的意识不强,过多依赖经验而缺少科学分析的方法和手段.
笔者认为,学情分析可以从以下4个方面进行:知识基础、思维方法、认知策略、情感态度.对于知识基础的分析要强调系统和整体的观点,要强化核心知识的教学,如本节课中用待定系数法求二次函数解析式及二次函数的性质需要强化和再认识.思维方法是学科育人不可或缺的重要环节,要根据学科特点选择合适的、科学的思维方法解决问题,学会认识自然和世界的方法.认知策略是指学生在感觉、知觉、思维、记忆和理解问题等认知活动中加工和组织信息时所采用的方法,认知的方法同具体的学习方法和思维方法是密切关联的,特别需要研究学生的思维监控能力,在思维活动中能反思、调节自己的思维方式,优化思维方法和过程.
3.2 强化思维方法
数学的学习不仅是解题,为记住解题方法做大量练习,通过强化训练提高思维能力,这些做法都是舍本逐末的短期行为.在高考指挥棒的影响下,这种情况在中学数学教学中还是普遍存在的,教师的教育观念需要进一步更新,为谋求学生长远发展展开教学.数学是一门发展学生思维能力的基础学科,数学教师应该厘清知识与技能、数学思想方法与数学思维方法的区别和联系,有意识地强化科学的思维方法.
从方法论视角来看,常用的科学思维方法有:观察与实验、比较与类比、归纳与演绎、分析与综合、一般化与特殊化、联想与猜想等.这些思维方法在本节课中都有体现,计算三角形的面积就是分析和综合的结果,从计算特殊三角形面积到用函数表达三角形面积,再到用方程求解点的坐标就是一般化与特殊化的最好体现,几何图形的分割和补形需要学生观察和操作,要有直观的想象和理性的演绎推理.从学情来看,学生对于科学思维方式的掌握不够深刻,没有达到熟练运用的程度,教学中需要强化.
3.3 发展核心素养
素养不只是知识与技能.它是在特定情境中,通过利用和调动心理社会资源(包括技能和态度)以满足复杂需要的能力.世界经济合作和发展组织认为素养就是在新的情境下运用所学知识解决问题的能力.这种新的情境并不是学生经过训练后程序化的操作,而是在一定思想和观念指导下形成的关键能力.本节课的设计需要学生会计算、会推理、会建模、会创新,创造性地解决问题,把数学核心素养落实在课堂上,在学情分析的基础上预设和生成[1].
