上海市中小学建筑能耗定额研究

余婉璇

上海众材工程检测有限公司

0 引言

上海市中小学校众多，目前却缺乏相应的能耗定额标准，建立合理的能耗定额指标体系对推进上海市中小学校节能减排有着重要的促进作用。

近年来，国内许多研究人员对学校用能情况和能耗定额进行了调查研究。2013 年，薛世海等人采用回归分析法给出按生均建筑面积分段方法制定的湖北高校能耗定额[1]。2017 年，喻凡等人采用分级定额分析方法得出夏热冬暖地区中小学校能源和水资源消耗水平[2]。2018 年，唐文龙等人利用统计定额法计算南京市中小学校园建筑能耗定额，并依据生均建筑面积和班级人数对建筑能耗定额进行修正[3]。2020 年，张慈枝等人运用统计分析方法确定各类高等院校的能耗定额[4]。在此基础上，本文将通过对上海市部分中小学校能耗数据进行分析，研究相关能耗影响因素，探究科学合理的中小学建筑能耗定额方法。

1 中小学能源消耗现状及影响因素分析

1.1 研究对象

本文基于学校能源审计，以上海市多个区96 所中小学校为研究对象，其中包括36 所小学，23 所九年制学校，37 所中学，对学校2019 年建筑能耗账单、建筑面积、空调面积、学生人数、用能人数等信息进行了收集。学校建筑用能包括电力、天然气、柴油等，电力主要用于校内各种电器设备，天然气、柴油主要用于厨房、锅炉等燃气设备。

1.2 能源消耗情况

本文将针对学校2019 年用能数据进行分析，并按表1 数据折算成标煤，得到建筑能耗等价值。

表1 各种能源折标系数

使用Excel 软件对中小学单位面积建筑能耗进行统计分析，结果如图1 所示。小学单位面积建筑能耗等价值位于4.7～14.88 kgce/m2之间，中位数为10.12 kgce/m2，均值为9.74 kgce/m2。中学单位面积建筑能耗等价值位于4.08～11.92 kgce/m2之间，中位数为7.64 kgce/m2，均值为7.85 kgce/m2。九年制学校单位面积建筑能耗等价值位于3.83～15.29 kgce/m2之间，中位数为8.27 kgce/m2，均值为9.04 kgce/m2。可以看出，小学单位面积建筑能耗普遍高于中学，九年制学校则分布范围较宽，均值介于小学和中学之间。

图1 中小学单位面积建筑能耗等价值

1.3 建筑能耗影响因素分析

通过对学校建筑用能数据的整理分析，相关因素可能为学生人数、建筑面积、空调面积等。本文将以上三个因素简化为生均建筑面积和生均空调面积两个参数。从图2 生均能耗曲线、生均建筑面积曲线、生均空调面积曲线，可以看出这三个参数可能存在相关性。

图2 学校建筑用能数据相关因素分析

使用SPSS 软件对生均建筑面积和生均空调面积这两个参数与单位面积能耗指标和生均能耗指标的相关性进行进一步分析，分析结果见表2。

表2 建筑能耗指标与影响因素的相关系数

从表2 可以看出，小学单位面积能耗与生均建筑面积成显著负相关。生均能耗则与生均建筑面积成显著正相关。中学和九年制学校单位面积能耗与生均建筑面积、生均空调面积均不相关。中学、九年制学校生均能耗均与生均建筑面积、生均空调面积则成显著正相关。

2 中小学能耗定额制定

国内学者已提出一些基于能耗统计的建筑能耗定额方法[5-6]，本文采用定额分析法确定中小学能耗定额。使用SPSS 软件对单位面积能耗和生均能耗进行正态分析，分析结果显示单位面积能耗服从正态分布，生均能耗则不服从正态分布。图3 为不同类型中小学建筑单位面积能耗正态分布图，图4 为正态分布检验结果。

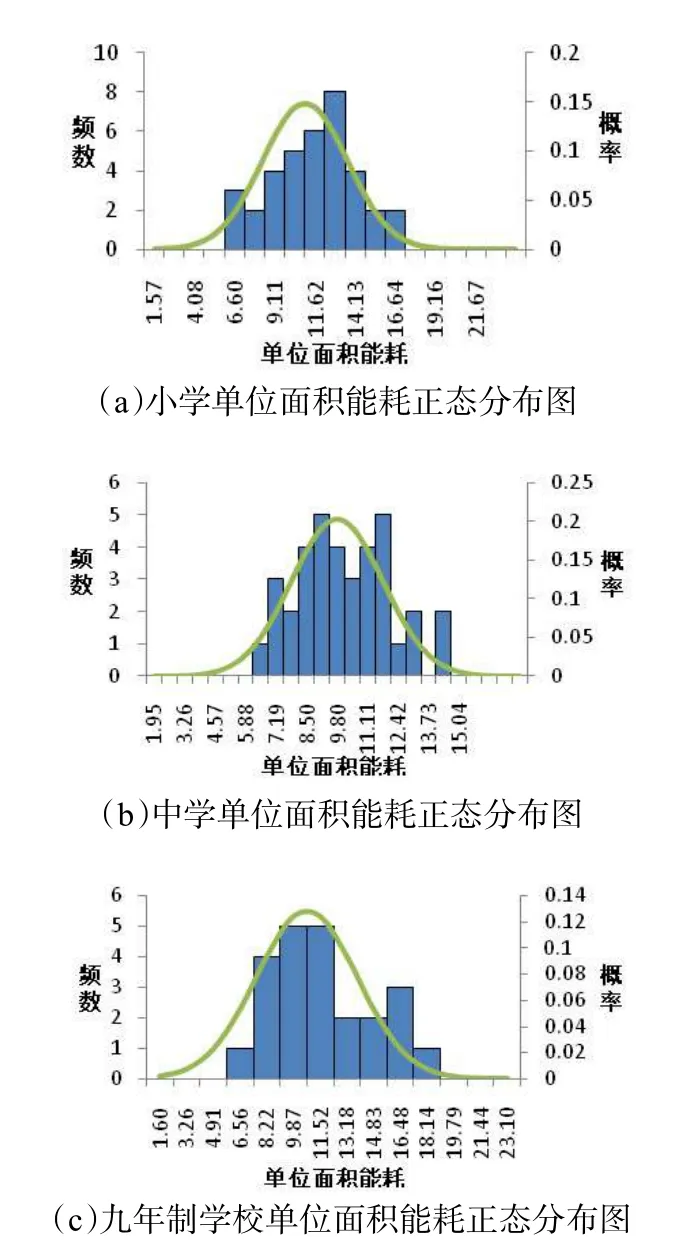
图3 不同类型中小学建筑单位面积能耗正态分布图

图4 不同类型中小学建筑单位面积能耗正态分布检验

式中：Za表示累计概率为(1-a)时所对应的标准正态分布概率密度值。

对各分类样本不同定额水平下的能耗进行计算，得到建筑定额水平表，如表3 至5 所示。

表3 小学单位面积能耗定额水平表

表4 中学单位面积能耗定额水平表

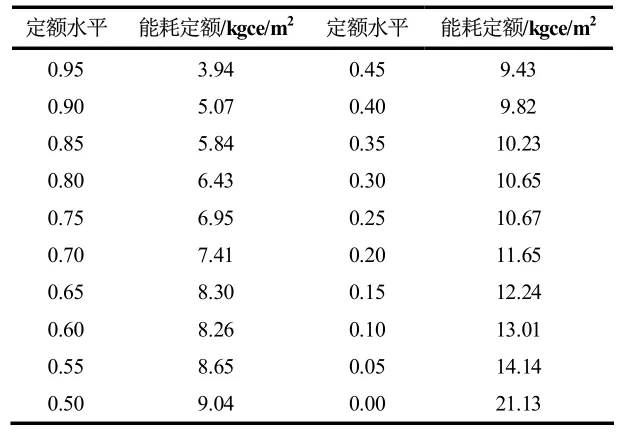
表5 九年制学校单位面积能耗定额水平表

选取累计概率以20%，50%，80%作为限定值，基准值和先进值，得到上海市中小学建筑单位面积能耗定额值如表6 所示。限定值表征能耗定额上限，基准值表征能耗利用平均水平，先进值表征能耗利用先进水平。

表6 上海市中小学单位面积能耗定额值

3 建筑能耗定额修正系数计算

3.1 单位面积能耗回归模型

前文分析可知，能耗定额中生均能耗与生均建筑面积和生均空调面积这两个影响因素相关性更显著。为了得到更准确的回归模型，本文使用SPSS/Excel 软件针对生均能耗指标进行回归分析，得到回归模型如表7 所示。表中，Y 表示生均能耗，kgce/生；X1表示生均建筑面积，m2/生；X2表示生均建筑面积，m2/生。

表7 生均能耗回归模型

根据单位面积能耗与生均能耗的关系（见式2），由生均能耗回归模型得到单位面积能耗回归模型如表8 所示。

表8 单位面积能耗回归模型

式中：Y'为单位面积能耗，kgce/m2；X3表示空调面积占比，%。

3.2 生均建筑面积分段

对中小学生均建筑面积进行统计分析，小学生均建筑面积均值为9.67 m2/生，中学生均建筑面积均值为21.43 m2/ 生，九年制学校生均建筑面积均值为13.41 m2/生。依据生均建筑面积均值及分布情况将其划分为三个区段，如表9 所示。

表9 生均建筑面积分段

3.3 空调面积占比分段

对中小学空调面积占比进行统计分析，中学空调面积占比均值为0.34 m2/生，九年制学校空调面积占比均值为0.36 m2/生。由于小学能耗与空调面积不相关，故不对小学进行空调面积占比统计分析和修正。依据空调面积占比均值及分布情况将其划分为三个区段，如表10 所示。

表10 空调面积占比分段

3.4 建筑能耗定额修正系数

已知单位面积能耗Y'与两个自变量X1、X3相关，X1为生均建筑面积，X3为空调面积占比，n 为分段区间样本数，则X1,k在X1,1至X1,n之间取值，X3,k在X3,1至X3,n之间取值，代表自变量X1的样本平均值,代表自变量X3的样本平均值。Y0为各自变量取样本平均值时的单位面积能耗。当其中一个自变量取平均值时，计算因变量Y'与Y0的比值α 。

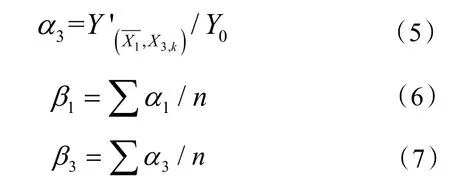
式中：β1为生均建筑面积修正系数；β3为空调面积占比修正系数。

根据以上公式计算得到不同分段区间修正系数，相关因素位于平均值分段区间时不予修正，反之则进行修正。修正系数见表11 和表12。

表11 生均建筑面积修正系数

表12 空调面积占比修正系数

用Ea表示单位面积能耗定额，则修正后的能耗定额Ea'为：

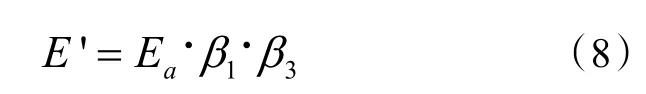
使用修正后的能耗定额Ea'对不同中小学能耗进行判定比修正前能耗定额Ea更加合理。

4 结论

通过对上海市多家中小学能耗数据进行分析，得到结论如下：

1）中小学能耗指标与生均建筑面积和生均空调面积成显著相关。

2）使用单位面积建筑能耗作为中小学能耗定额指标更为合理，同时使用定额分析法得到不同类型中小学的能耗定额值。

3）通过回归分析法得到能耗回归模型，同时使用该模型对生均建筑面积和空调面积占比两个参数进行修正，得到不同区段的修正系数，建立科学可行的中小学建筑能耗定额指标体系。