中国林业绿色全要素生产率的时空演变分析

吕洁华，孙嘉宇，蔡秀亭

（东北林业大学经济管理学院，黑龙江哈尔滨 150040）

一、引言与文献综述

生态文明建设是我国全面建成社会主义现代化强国的重要一步，是关系经济社会、人民福祉和民族未来的长远大计。林业产业作为绿色产业，在完善传统生产结构单一模式后，为经济建设和生态建设作出重要贡献。然而，长期以来我国林业发展存在的技术水平落后、生产效率低下、从业人员环保意识薄弱等问题严重制约林业经济的持续稳定发展［1］。党的十八届五中全会以后，“绿色”成为新发展理念之一，经济发展与资源环境保护相协调成为新的发展潮流。“十四五”规划提出：林业发展要践行“绿水青山就是金山银山”理念，坚持高质量发展鲜明导向，走“经济生态化、生态经济化”现代林业发展道路。而我国林业发展在依赖大量投入资源实现经济腾飞后步入滞缓期，全要素生产率开始成为林业实现长期增长的根本，主要包括技术创新、规模效应等要素投入以外影响效率的动力来源。绿色全要素生产率逐渐成为考察经济效率的重要指标，而对林业绿色全要素生产率的全面把握将有助于稳定发展资源节约型、环境友好型林业产业。

全要素生产率最初表示单一要素生产率，逐步演变为多种投入要素对经济增长的贡献率，能更加准确地衡量经济活动效率［2］；而后基于经济假设与实际的符合程度，全要素生产率具体定义为要素投入对经济增长贡献以外的其他因素的贡献量［3］。林业发展进入要素驱动增长的瓶颈时期，全要素生产率成为推动林业经济增长的重要着力点。史常亮等［4］研究发现，中国林业全要素生产率水平较低，主要由于林业生产技术效率低下，技术无效率现象普遍存在，也表明林业技术进步是驱动林业发展的主要因素［5］。而陈向华等［6］研究黑龙江省林业生产效率时得出不同结论，即全要素生产率低下主要是由于林区技术落后所致。地区间资源禀赋、经济实力、技术创新水平等不同势必导致林业生产效率的差异。徐玮等［7］研究发现我国中部地区属于林业较发达地区，但未达到效率最优，而其余地区林业效率处于最佳状态；基于多重效益目标，黄安胜等［8］研究发现，地区间林业全要素生产率及其分解水平迥乎不同，主要源于潜在的驱动因素差异。同时，全国范围内产业网络的完善，在一定程度上打破产业间市场壁垒，促使林业全要素生产率的空间差异降低，呈收敛发展趋势［9］。此外，林业产业的空间溢出效应以及相似的经济、资源、政策条件会推动林业在空间上形成集群，全要素生产率水平呈现集聚分布［10］，而林业产业空间集聚可进一步影响地区林业全要素生产率水平［11-12］。

为推动林业全要素生产率，促进林业经济发展，学者们广泛搜寻影响林业全要素生产率的因素，深入挖掘其内部作用机制。曹玉昆等［13］研究发现，国家对林业的财政支持能有效推动林业全要素生产率增长；董娅楠等［14］研究认为，林业全要素生产率受当期FDI 水平影响不显著，而对于滞后一期的FDI 具有正向反馈，表现出外商直接投资对林业产业的影响具有一定时滞性；揭昌亮等［15］深入分析进出口贸易对林业生产效率的影响，发现产业在参与国际贸易活动过程中可以改变企业生产技术和规模经济，进而影响全要素生产率。另外，刘东等［16］还探究林业发展基础水平、人力资本水平、造林护林投入等因素对林业全要素生产率的影响。

随着社会对生态环境关注度提高，全要素生产率与生态环境的结合更符合高质量发展要义，绿色全要素生产率也广泛用于效率测算［17］。学者们较早展开对林业可持续发展的相关研究，如郎晓娟等［18］从绿色经济视角下分析发现，产业的“绿色投资”“绿色创新”“绿色新政”将会提升林业全要素生产率，推动产业高质量发展；刘清泉等［19］从可持续发展视角探究广东省林业全要素生产率和地区经济的协同发展关系。然而，直接将生态环境资源要素加入到林业全要素生产率测算的研究尚处于起步阶段。沈伟航等［20］发现林产工业的绿色全要素生产率增速减缓，主要原因是纯效率的下降；刘涛等［21］创新性测算中国林业绿色全要素生产率，发现其在效率和技术进步双驱动下呈增长趋势，但在空间范围内却呈现非均衡分布，并进一步分析政府支持等因素对地区林业绿色全要素生产率的影响。

综合来看，国内外学者对林业全要素生产率的测算及影响因素研究比较充足，但对于林业绿色全要素生产率的研究仍处于起步阶段，缺少对其时空演变的定量分析以及状态转移分析。基于此，本文采用超效率SBM 模型重新测算我国林业绿色全要素生产率，结合区域差异性分析及马尔可夫转移客观探究其演变历程并进行长期预测，把握基本演变规律，为推动林业“经济生态化，生态经济化”发展提供科学依据。

二、理论分析与研究假说

20世纪30年代，柯布和道格拉斯提出的C-D 生产函数揭示经济活动的要素投入和产出关系，归纳资本、劳动力以及除此以外的其他部分因素为实现经济活动的源泉。在此基础上，索罗于20世纪50年代提出具有规模报酬不变特性的总量生产函数，确定资本及劳动力以外的因素为全要素生产率，并将其归结为技术进步。20 世纪80 年代中期，内生增长理论进一步确定内生的技术进步是实现经济长期增长的决定因素，也表明全要素生产率的增长是实现经济长期稳定增长的根本动力来源。而林业绿色全要素生产率综合考虑林业经济发展动能与生态资源环境保护的思想，是林业产业实现绿色可持续发展的重要测度指标。

由于林业产业具有高度的资源环境依赖属性，同时各区域林业产业在后期的生产活动中自发产生知识信息交流，使得林业绿色全要素生产率在长期内呈现出发散或收敛态势。因此，假定林业绿色全要素生产率长期内有区域内和区域间两条演变路径。

地理学第一定律揭示任何事物在空间范围内都存在关联，且关联度与相邻距离呈反比关系，即距离越近，关联程度越高。林业发展对基础林业产业的依赖性较高，即林业产业厂商倾向于选择靠近林业资源丰富的区位，由此诱导林业产业在资源充裕位置形成集群。同时，林业企业在竞争发展过程中存在知识和信息交流、技术学习模仿等行为，使区域内企业关联度提高，带动区域内企业经济运作模式、生产效率逐渐趋同。最终林业发展表现为，地区林业全要素生产率对周边区域林业绿色全要素生产率提高具有溢出效应，区域内林业绿色全要素生产率差异减小，从而呈现出空间范围内的相似发展，演变成时序上的收敛趋势。基于此，提出第一个研究假说：

H1：林业绿色全要素生产率在区域内由于空间溢出效应呈现收敛态势。

地理学第二定律的提出同时证实，事物的空间隔离性造成事物在地理范围内的差异。由于各区域在资源禀赋、经济发展水平、技术创新能力、生态环境及政策制度等方面存在明显差异，势必促使林业产业向不同方向发展，导致区域间产业经济运作模式、生产效率的差异。在空间范围内，不同林业全要素生产率水平的企业最终出现差异性集聚分布，区域间林业绿色全要素生产率呈现时序发散趋势。基于此，提出第二个研究假说：

H2：林业绿色全要素生产率在区域间由于空间异质性呈现发散态势。

三、数据来源、变量选取与模型选择

（一）数据来源

由于《中国环境统计年鉴》于2004年开始对我国环境和林业土地等指标进行系统的核算，因此为保证数据的测算口径一致，本文选取的研究期间为2004—2019 年。由于我国香港等地区数据缺失，因此只考察其余30个省（市、自治区），数据主要来源于《中国统计年鉴》《中国林业统计年鉴》《中国环境统计年鉴》《中国能源统计年鉴》等。其中，固定资产投资额采用固定资产投资指数平减，其他指数采用居民消费价格指数平减。

（二）变量选取

本文研究的核心变量为林业绿色全要素生产率，参考刘涛等［21］已有研究，确定林业绿色全要素生产率测算指标体系（表1）。投入要素包括土地、资本、劳动力和能源，土地、资本和劳动力分别采用林业用地面积、林业固定资产投资存量［22］和年末林业从业人数表示，能源投入采用“地区能源消费总量×地区林业总产值/地区生产总值”方法测算。期望产出包括经济产出和生态产出，分别用地区林业生产总值和地区造林面积表示。非期望产出主要为环境污染物排放量（产出量），采用“地区工业污染物排放量（产生量）×地区林业第二产业产值/工业生产总值”方法测算林产工业SO2排放量、林产工业废水中COD 排放量和林产工业固体废弃物产生量表示。林业全要素生产率的测算不考虑土地、能源投入以及非期望产出。

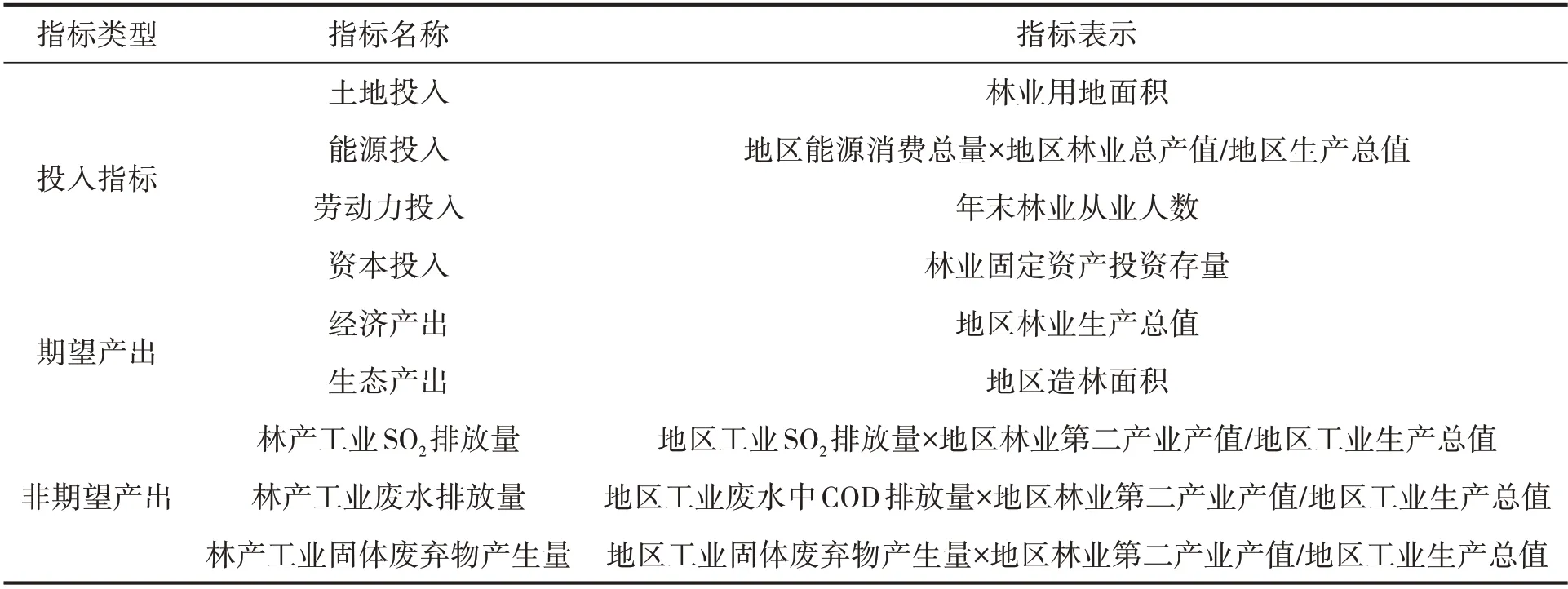
表1 林业绿色全要素生产率测算指标体系

（二）模型选择

1.超效率SBM 模型 超效率SBM 模型综合考虑影响决策单位效率水平的各投入产出要素之间的非线性关系，确定决策单位的效率水平。相较于传统数据包络模型，超效率SBM 模型将非期望产出要素考虑到决策单位的效率测算，同时可以非径向调整投入产出的松弛变量，最大程度改善效率值。综合比较，超效率SBM 模型独有的特性更加符合林业绿色全要素生产率测算需求，因此本文采用超效率SBM 模型测算林业绿色全要素生产率，将决策单位不同效率水平加以明确区分。超效率SBM 模型具体表示为：-

2.泰尔指数 本文采用泰尔指数度量各地区林业绿色全要素生产率在区域间的差异，具体表达式为：

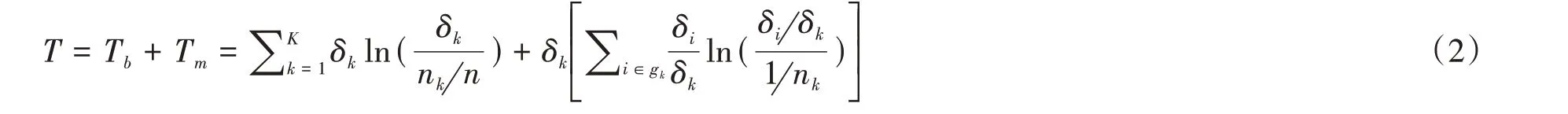
式（2）中，T表示区域间差异的总体泰尔指数，n表示研究区域的数量，δi表示i地区的林业绿色全要素生产率，-δ为其平均值。当将n个地区划分为K组，则每组的地区数量为nk，总差异可划分为组间差异（Tb）和组内差异（Tm）。

3.核密度函数 核密度函数是基于核函数通过采用平滑估计以确定随机变量概率密度的分布形态的方法［23］，采用核密度函数研究林业绿色全要素生产率区域差异演变状况。具体表达式为：

式（3）中，K(*)为核密度函数，h表示带宽，最大带宽的确定应满足积分局方误差值最小。

4.莫兰指数 为探究林业全要素生产率的空间相关性特征引入莫兰指数，全局莫兰指数表达式为：

5.马尔可夫链 马尔可夫转移是一个随机过程，其假定研究对象状态只与前一期状态有关。而林业发展效率状态会在前一期效率水平上进行投入产出调整以达到期望效率值，而更前期的效率水平对其影响较不明显，因此可以假定林业绿色全要素生产率符合马尔可夫转移的应用前提。马尔可夫转移根据数据分布将指标值分为l个状态类别，再根据不同状态转移频数确定转移概率。具体计算公式为：

式（6）中，pαβ表示t时期状态为α，后一时期为β的概率，nαβ表示t时期林业绿色全要素生产率状态为α，后一时期为β状态的频数；nα表示t时期状态为α的个体数量。空间马尔可夫链可考虑相邻区域状态影响，采用Rook 临界方法确定空间权重，计算空间滞后类型，根据同样计算概率的方法最终确定l个（l×l）的条件转移概率矩阵。基于马尔可夫转移矩阵，对林业绿色全要素生产率转移进行长期预测，具体公式为：

式（7）中，S表示长期马尔可夫转移概率矩阵，M是已知转移概率矩阵。

四、结果与分析

（一）林业绿色全要素生产率与林业全要素生产率描述性分析

采用DEA Solver 软件中超效率SBM 模型测算我国30 个省（市、自治区）林业效率值，由于篇幅有限，此处仅列示2004、2010、2015 以及2019 年代表性年份测算值（表2）。

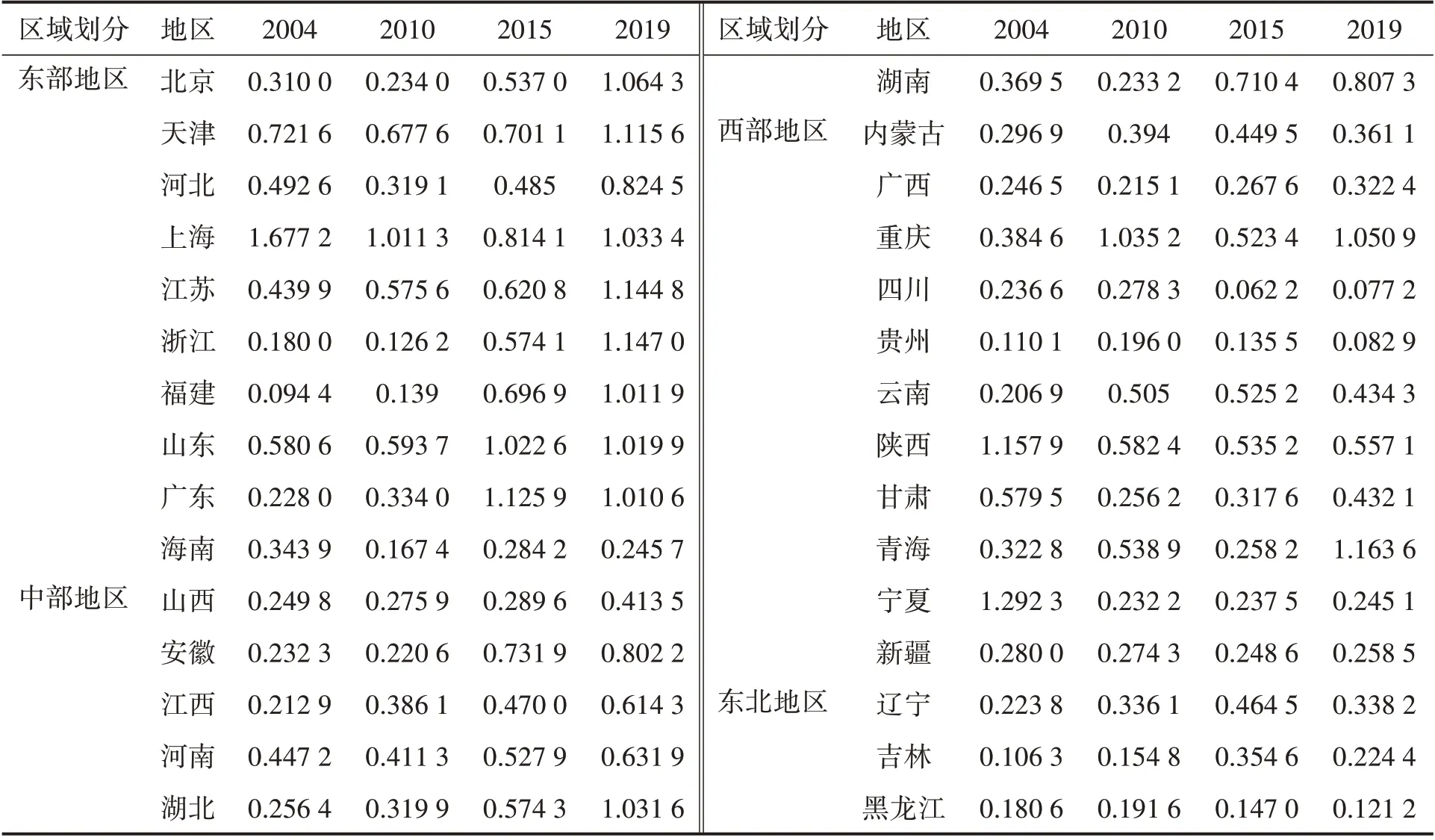
表2 代表性年份林业绿色全要素水平

从表2 看出，2004 年我国大部分地区林业绿色全要素生产率处于低水平和中低水平，而处于中高水平和高水平的省份多集中在黄河流域，包括宁夏、陕西和上海。2010 年相对于2004 年大部分地区效率值出现轻微波动，但仍多处于低水平。其中甘肃、宁夏和陕西效率值明显下降，青海和重庆效率值明显升高，效率值在空间上呈现无规律分布。2015 年与2010 年相比，中东部地区以及云南效率值明显提高，效率值在空间范围内出现较明显区域分布差异。2019 年大部分地区效率值改善，其中青海、重庆和浙江效率值明显提高，而效率值较低地区主要分布在东北地区和西南地区以及部分西部地区。

对比全国平均水平（图1）可得，两者整体呈现增长趋势，表明我国林业生产效率逐渐提高。而林业绿色全要素生产率明显高于林业全要素生产率，且波动明显。表明林业资源能源投入所带来的经济效益高于发展所导致的环境低效率，进一步说明林业绿色全要素生产率更能真实反映林业发展现状。

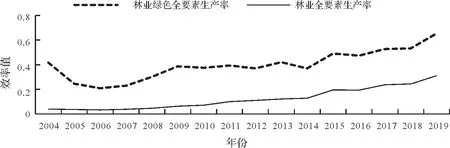
图1 全国林业全要素生产率及林业全要素生产率平均水平

对比四年林业绿色全要素生产率空间变动发现，优势区域从黄河流域转移到中东部地区，经济崛起带动林业发展，空间集聚效应逐渐呈现。林业产业经过2010—2019 年十年发展努力，多数地区效率值扭转起初不利局势。但东北及西南部分地区效率值仍较低，表明该部分地区生产效率改善及整体均衡发展具有较大提升空间。对比2004 与2019 年林业绿色全要素生产率，大部分地区效率值向更高水平转移，表明林业正在向高质量发展阶段推进。西部部分地区及海南有所降低，主要受制于地区经济技术和自然条件水平。东北和西南地区效率值虽然始终处于低水平，但整体效率值升高，表明该部分地区具有突破低效率水平的内在发展潜力。

（二）林业绿色全要素生产率区域差异分析

1.区域差异收敛性分析 采用Stata15 软件计算2004—2019 年林业绿色全要素生产率泰尔指数，并依据我国四大经济区域进行分组，测算组间和组内泰尔指数（图2）。从总体泰尔指数看出，2004—2009 年区域间差异呈现“锯齿状”波动，2009 年后波动幅度明显减小。2015—2019 年指数值达到平稳状态，但仍存在发散趋势。而2004—2015 年的组内泰尔指数与整体泰尔指数的变动趋势保持一致，表明此期间差异主要来自组内差异，经济区域间差异较小。2015—2019 年组间泰尔指数明显升高，达到与组内泰尔指数相当的水平，表明要实现长期内收敛需控制经济区域间林业绿色全要素生产率差异。

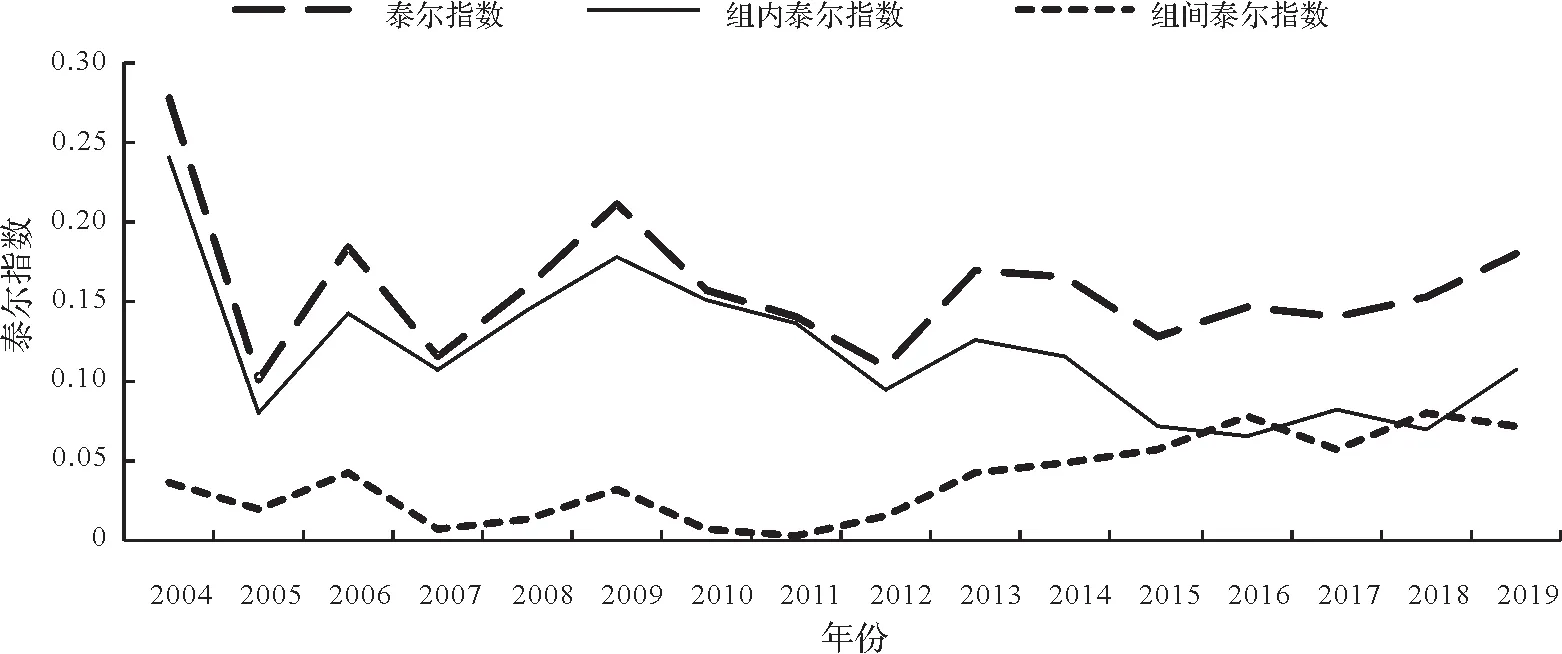
图2 林业绿色全要素生产率区域差异

从图3 各经济区域对总体泰尔指数贡献率来看，中部和东北地区对区域总差异的贡献程度较稳定，东北地区贡献最小。在2004—2011 年，东部地区和西部地区指数贡献率处于互补波动状态，是总体差异主要来源。2011 年以后西部地区的差异不断减小到与中部地区贡献率相近的水平，而东部地区的贡献率仍处于上升趋势，是未来区域差异的主要来源。

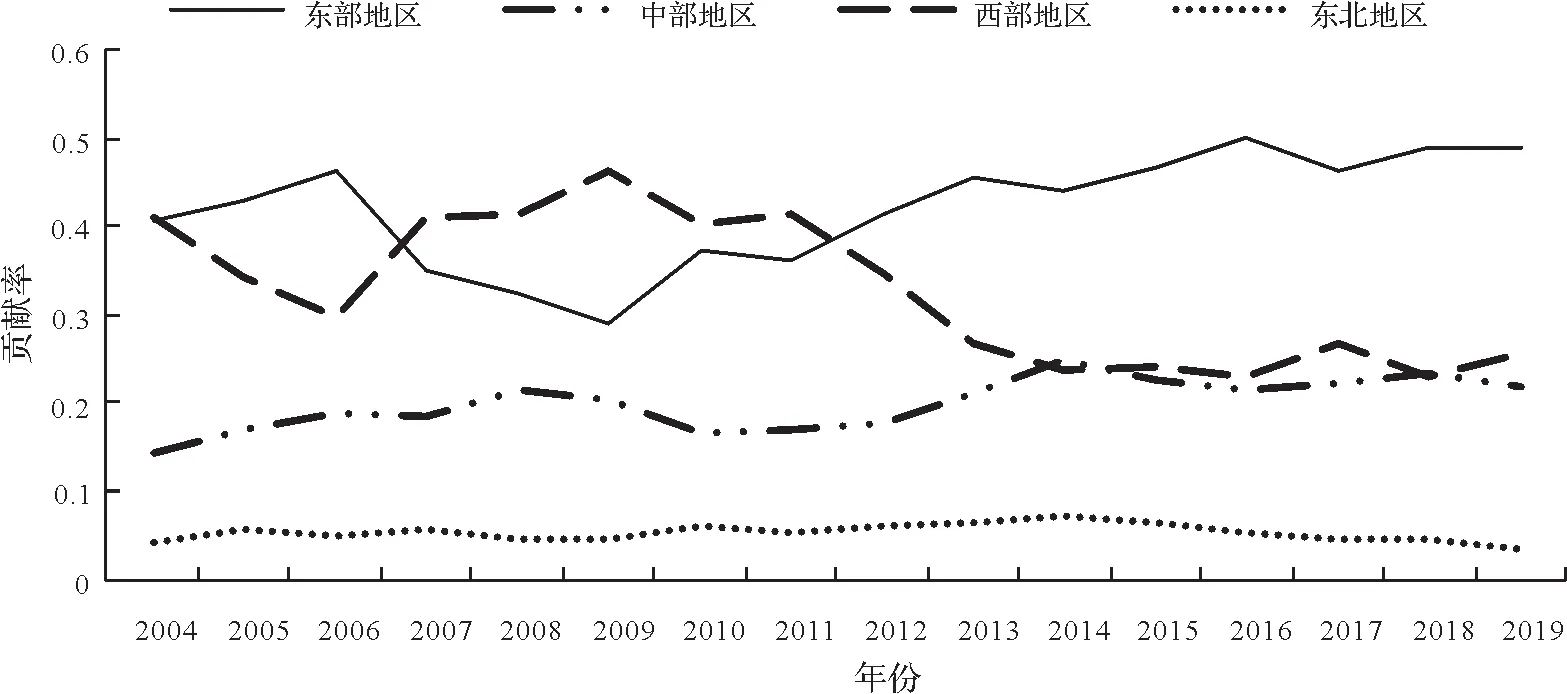
图3 各经济地区泰尔指数贡献率

2.区域差异核密度估计分析 采用高斯核密度函数明确地区差异的演变过程，同时采用Stata15软件绘制2004、2010、2015和2019年的林业绿色全要素生产率核密度图（图4）。

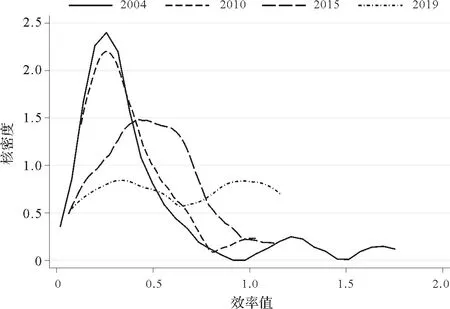
图4 代表性年份林业绿色全要素生产率核密度图

2004 年核密度曲线呈现单峰形式，且峰值处于低于0.5 区间，表明多数地区效率值较低。但核密度曲线存在向右拖尾现象，表明少部分地区效率值较高。2004—2010 年核密度曲线峰值变动不大，但拖尾现象减弱。2015 年核密度曲线峰值明显下降且向右移动，宽度增加，表明2015年效率值分布较2010年更加均匀，整体效率值有所提高。2019 年拖尾现象明显转化为核密度曲线呈现双峰形态，各地区林业绿色全要素生产率呈现轻微两极化分布。双峰峰值较小，宽度较大，效率值集中度降低。

（三）林业绿色全要素生产率空间自相关分析

表3 计算林业绿色全要素生产率的全局莫兰指数。数据显示，在2004—2012 年，只有2005 年存在轻微的空间正自相关性，其余年份林业绿色全要素生产率大多呈现随机分散分布状态。而在2014—2019年，空间正自相关明显增强，林业发展的空间集聚特征不断呈现。

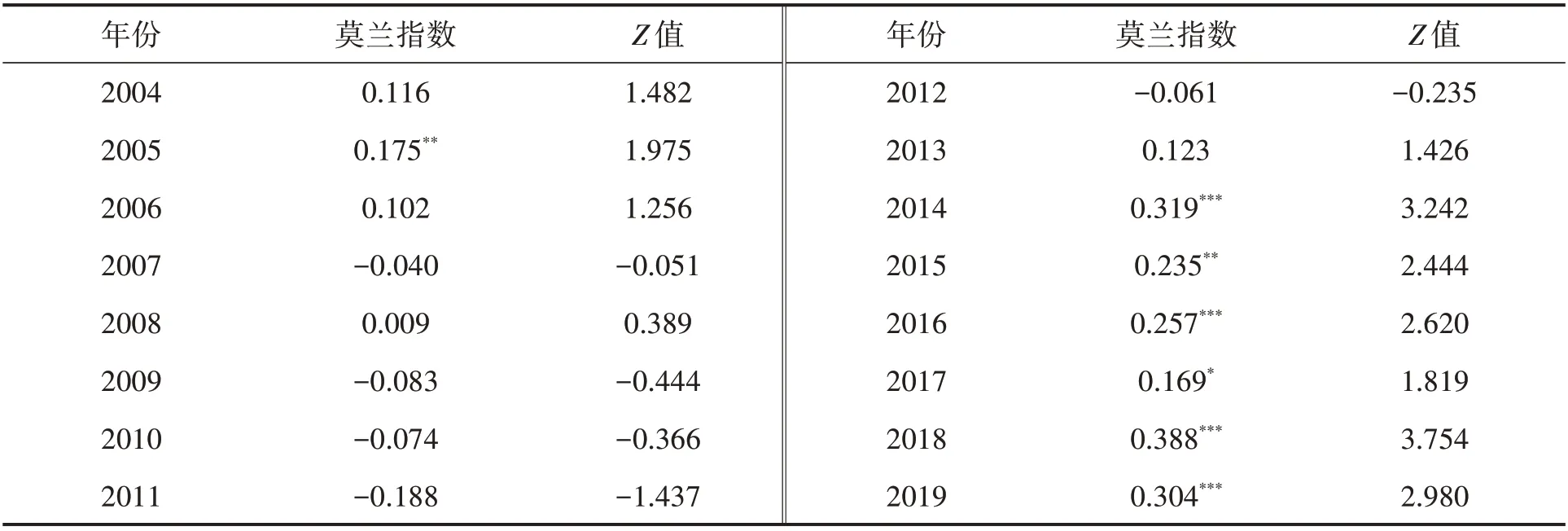
表3 林业绿色全要素生产率全局莫兰指数

为进一步测算2016—2019年林业绿色全要素生产率局部莫兰指数，本文绘制局部莫兰指数散点图进行区域空间集聚特征分析。2016—2019 年，多数地区处于第一象限（H-H 集聚区域）和第三象限（LL集聚区域），空间正自相关性明显，与前文全局莫兰指数分析结果一致，少数地区如广西、浙江、海南处于第二象限（L-H 集聚区域）。处于第一象限的地区多为中东部地区，而处于第三象限的地区多为西部地区和东北部地区，表明效率值较高的地区集聚在中东部地区，而效率值较低的地区集聚在西部以及东北地区，林业绿色全要素生产率在空间内呈现两极化分布。

（四）林业绿色全要素生产率状态转移分析

1.短期区域状态转移分析 根据林业绿色全要素生产率的分布情况将效率值分为低（Ⅰ）、中低（Ⅱ）、中高（Ⅲ）和高（Ⅳ）4个水平等级，分别将2004—2019年30个省（市、自治区）的效率值依据不同等级的范围进行状态归类，得出处于各等级的个体频数，计算状态转移概率，最终确定传统马尔可夫转移概率矩阵和空间马尔可夫转移概率矩阵（表4）。

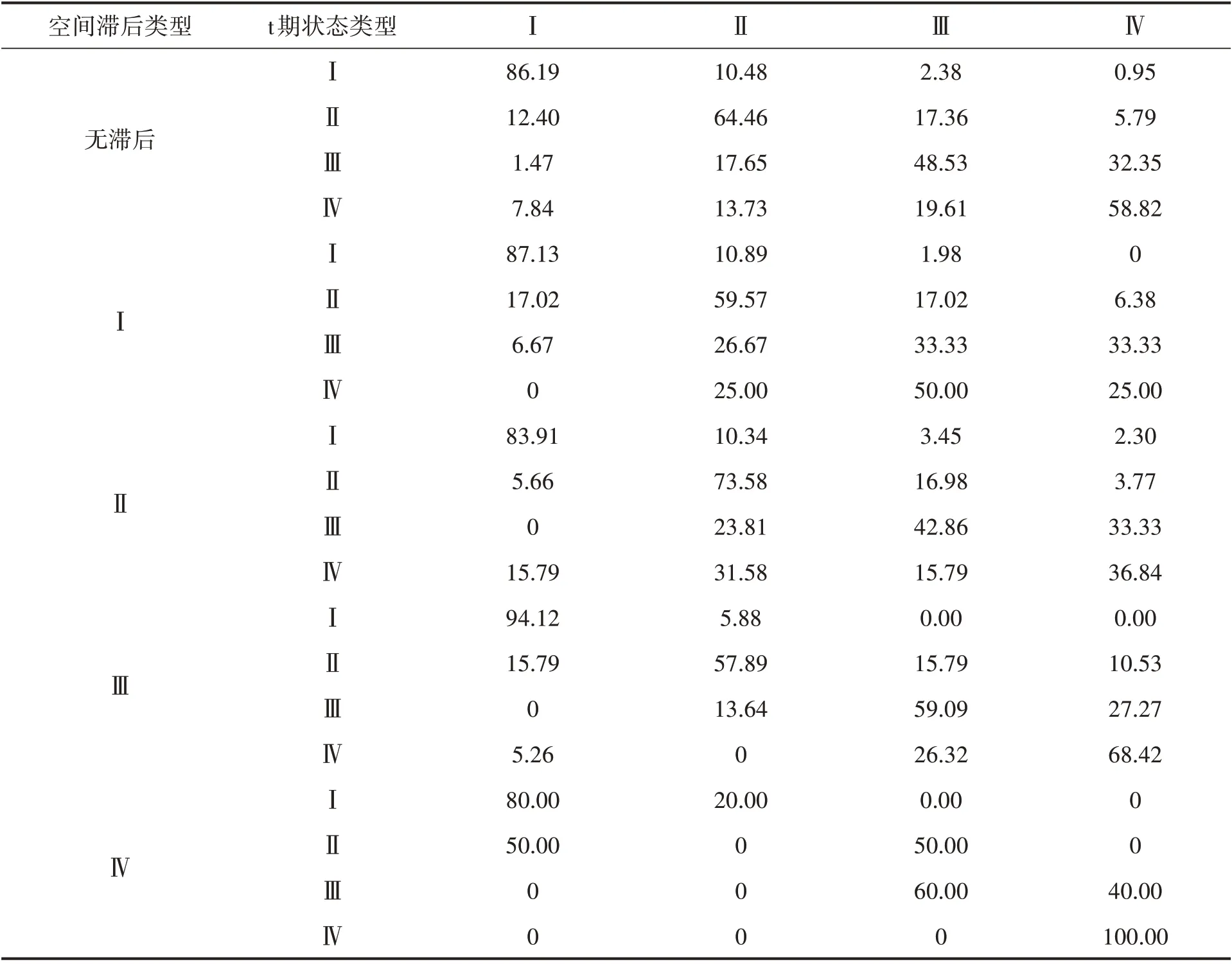
表4 林业绿色全要素生产率传统和空间马尔可夫转移概率矩阵 %

对传统马尔可夫转移概率矩阵进行分析发现，马尔可夫转移概率矩阵主对角线上概率值均高于非主对角线上的概率值，类型Ⅰ、Ⅱ、Ⅲ、Ⅳ保持其初始状态的概率分别为86.19%、64.46%、48.53%和58.82%，均大于转移为其他状态类型的概率。其中类型Ⅰ保持初始状态的概率最高，表现低效率水平地区林业绿色全要素生产率的持续性。这表明林业绿色全要素生产率保留其初始状态的概率较高，林业绿色全要素生产率转移存在“俱乐部效应”。另外，转移概率矩阵中效率值向上转移的概率高于向下转移的概率，如矩阵中类型Ⅱ转移为类型Ⅲ和Ⅳ的概率比例为23.15%，明显高于转移为类型Ⅰ的概率（12.4%），其他状态类型类似。表明林业绿色全要素生产率具有向好发展趋势，我国林业倾向于向更高效率水平发展。再次，矩阵中邻近主对角线的概率值高于非邻近的概率值，如矩阵中类型Ⅰ转移为类型Ⅱ的概率为10.48%，大于转移为类型Ⅲ和类型Ⅳ的概率（3.33%），此规律同样适用于向下转移的情况。这表明林业绿色全要素生产率转移对初始状态类型具有一定的依赖性，难以实现跨级别转移。

将相邻区域效率状态考虑到林业绿色全要素生产率状态转移概率测算中，构建空间马尔可夫转移矩阵发现，在相应类型空间滞后状态影响下，林业绿色全要素生产率保持其初始状态的概率升高，如空间滞后类型为Ⅰ时，类型Ⅰ保持初始状态的概率提高到87.13%。这表明在相应空间滞后状态类型影响下，“俱乐部效应”增强，相似的生产效率水平将导致区域间信息、技术趋同，林业绿色全要素生产率状态持续性增强。另外以空间滞后等级高的区域为邻，效率值向上转移的概率升高，以空间滞后等级低的区域为邻，效率值向下转移的概率升高。如在不考虑空间滞后时，类型Ⅰ向上转移为类型Ⅱ、Ⅲ、Ⅳ的总概率为13.81%，在空间滞后类型为Ⅱ的情况下，相应转移概率升高到16.09%。表明林业绿色全要素生产率转移存在空间溢出效应，邻近区域效率状态对区域状态演变同时具有正向和负向溢出影响。在空间滞后影响下，林业绿色全要素生产率转移对初始状态仍具有较强依赖性。如空间滞后类型为Ⅰ的情况下，类型Ⅰ向类型Ⅱ转移的概率（10.89%）高于向类型Ⅲ和Ⅳ转移的总概率（1.98%）。这表明林业发展的流动性较弱，低效率水平地区短期内仍难以向高端状态推进。

2.长期区域状态空间演变预测 为探究林业绿色全要素生产率状态的长期变化，采用R 软件对马尔可夫转移概率矩阵进行长期预测，相对于短期状态转移规律存在一定的异同之处。

长期内林业绿色全要素生产率状态转移仍难以实现趋同，呈现向多个状态类型转移的趋势。从表5 可以看出，在不考虑空间滞后情况下，四种类型效率值转移呈现较均匀分布，在空间滞后类型为Ⅰ的情况下，长期转移概率集中在类型Ⅰ和类型Ⅱ；林业绿色全要素生产率长期转移具有空间收敛性，即效率值趋于向空间滞后类型方向转移。表现在矩阵中，状态转移为空间滞后类型的概率最高。如在空间滞后类型为Ⅰ的情况下，长期转移为Ⅰ类型的概率最高（46.11%），表明长期内相邻区域生产技术的溢出影响将使地区林业生产效率向空间滞后类型收敛，促使其呈现空间集聚分布。另外类型Ⅲ长期内趋于向类型Ⅰ转移，表明林业发展处于中高水平的地区在空间上过度集聚可能导致恶性竞争、市场失灵，进而影响产业生产效率。这警示处于中高水平的林业产业地区，若不及时进行产业调整，长期内仍可能陷入产业低效率发展陷阱；长期内，林业绿色全要素生产率转移具有空间溢出性，表现为当空间滞后类型为低水平或中低水平时，状态转移概率将集中在低水平或中低水平方向。而空间滞后类型为高水平时，状态转移概率将集中在高水平方向。该现象表明空间溢出性使得林业绿色全要素生产率在空间上呈现集聚分布。如空间滞后类型为Ⅰ的情况下，长期状态转移概率集中在向类型Ⅰ和类型Ⅱ转移，概率分别为46.11%和28.67%。相似结论适用于空间滞后类型为Ⅱ和Ⅳ的情况。

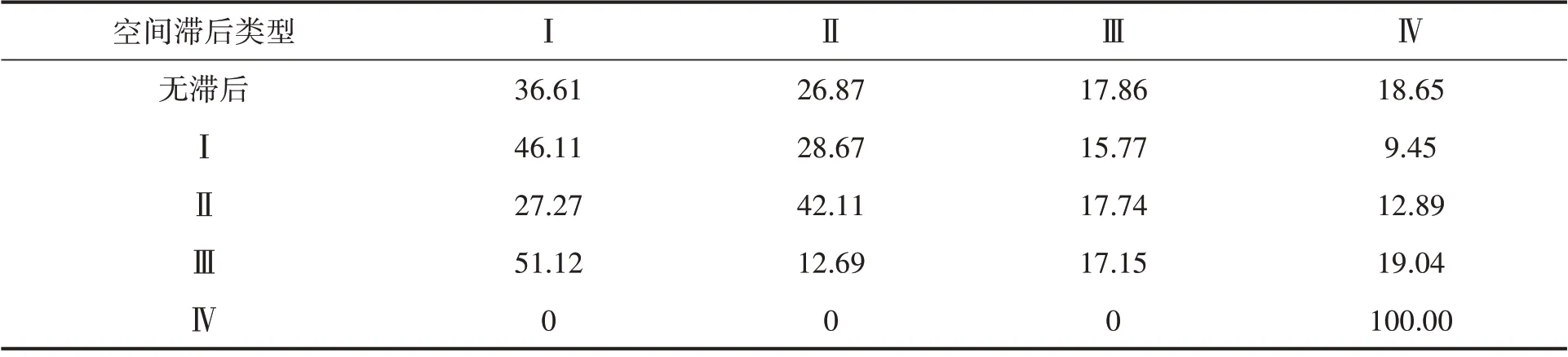
表5 林业绿色全要素生产率长期马尔可夫转移概率预测矩阵 %

五、主要结论与政策建议

采用超效率SBM 模型测算2004—2019 年我国30 个省（市、自治区）的林业绿色全要素生产率，在此基础上进行时空演变及状态转移分析。得到以下研究结论：第一，我国多数地区林业绿色全要素生产率实现了向更高效率水平转移，优势区域随经济重心转向中东部地区。第二，林业绿色全要素生产率地区间差异波动下降，且差异主要来自经济区域内部，但经济区域间差异影响不断提高。第三，2013 年后林业绿色全要素生产率空间正相关性明显，高效率区域聚集在中东部地区，低效率区域集聚在西部和东北地区，呈现出明显的两极分化局势。第四，从状态转移分析看出，短期内林业绿色全要素生产率具有向好发展趋势，但长期仍难以趋同；林业绿色全要素生产率状态转移存在“俱乐部效应”，对初始状态的依赖使得状态转移流动性较弱，而由于长期收敛，空间集聚分布明显，但过度空间集聚将导致中高林业绿色全要素生产率水平区域向低水平转移。此外，林业绿色全要素生产率状态转移存在空间溢出性。

基于上述研究结论，提出如下政策建议：首先，协同区域经济发展，共建良好宏观经济环境。推进东北地区振兴和西部大开发战略，加速地区优势资源引进，完善地区体制建设。同时要加强林业政策支持和善林业发展基础建设，完善林业产权保护相关法律法规，提高林场主生产积极性。其次，推动权利适度下放，引导区域创新竞争，有效利用产业集聚优势。政府要严格监督林业产业市场价格，明确赏罚机制。最后，促进区域交流，强化林业产业正向溢出作用，深化“以强扶弱”发展理念。推动落实中东部地区人才资源、信息技术向西部及东北部地区引进的优惠政策，完善区域间产业链，加强林业产业市场建设，协调推进地区林业产业发展。