BAS-RF组合算法在大坝水平位移预测中的应用

2022-09-09刘立龙梁月吉黄顺谋陈金磊

无线电工程 2022年9期

张炎，刘立龙*，梁月吉，徐勇，黄顺谋，陈金磊

(1.桂林理工大学测绘地理信息学院，广西桂林 541006；2.广西空间信息与测绘重点实验室，广西桂林 541006；3.郑州腾飞建设工程集团有限公司，河南郑州 450000)

0 引言

拦蓄水流的大坝通常可以带来显著的经济效益，然而一旦发生决堤事件，将会严重损害大坝周边人民的生命财产安全，实时掌握大坝的变形规律并做好预测至关重要[1]。经过长期的大坝监测研究发现，影响大坝变形的因素主要有气候、库水位、材料特性、时效和温度等，其中温度、时效和库水位占比重最大[2]。大坝位移是大坝变形的直接体现，其具备高度的非线性与随机性，传统的预测方法难以满足现今大坝变形监测的高精度要求[3]。随着大坝监测模式的不断改变，组合预测模型越来越多地应用到大坝变形监测领域中。陈波等[4]提出采用瑞利分布构造滞后函数，分析了大坝变形受到模拟寒区复杂温度荷载的影响，构建了考虑温度连续滞后效应和幅值削减效应的寒区混凝土坝变形预测预报模型。马广臣等[5]通过动态权重粒子群算法——自适应模糊神经网络组合法来构建大坝变形预测模型，利用改进粒子群算法对自适应模糊神经网络中模糊层的适应度值进行参数寻优，使预测模型的稳定性得到加强。胡清义等[6]采用将IDE应用于优选对OSVR中的惩罚参数和核参数，引入的自适应因子对基本差分进化算法进行改进，建立了坝体、坝基位移与材料参数的非线性关系，从而得到坝体及坝基变形模型。目前所提及的生物智能算法参数寻优存在运算效率较低且参数设置较为复杂的问题，需要进一步改进。

本文提出利用天牛须搜索(Beetle Antennae Search,BAS)算法优化随机森林(Random Forest,RF)算法来建立大坝水平位移预测模型。RF算法在许多领域已得到广泛的应用，其具备抗过拟合和预测精度高的优势。利用计算量低且运算速度快的BAS优化算法来为RF回归算法选取参数最优解，能够近一步提高模型预测的精准性。将改进后的模型应用于大坝水平位移的预测中，并与传统的预测模型进行对比，验证其稳定性及现实性。

1 天牛须搜索算法

2017年,Jiang等[7]提出了一种新的生物智能算法——BAS算法，也称为甲壳虫须搜索算法。天牛在觅食的过程中，主要是根据左右触须接收的信息来判别目标具体方位及距离，与蜂群算法、灰狼算法等相比，该算法仅需要一个独立个体，参数少、计算简单、搜寻速度较快[8-9]。具体过程是：天牛通过左右双须可以同时接收到食物散发气味的浓度，如果左触须收集到的食物气味的浓度高于右触须，则天牛向左触须提供的方向移动，反之，则向右触须提供的方向移动。整个过程实质上就是寻找散发气味最浓的食物的具体位置[7]。搜索过程如图1所示。

图1 天牛搜寻食物过程Fig.1 Process of longhorn beetles searching for food

根据天牛搜寻食物的过程，可以总结出天牛搜索算法的关键步骤:(1)根据天牛在现实中觅食的行为可以模拟出在虚拟世界中天牛在多维空间中计算函数极值的结果情况；(2)尽管实际天牛的左右两须长度不一，虚拟天牛必须保持左右两须相互对称；(3)天牛觅食过程中，身体前进方向具备随机性，且移动距离与左右触须间距离成比例。具体过程如下：

① 确定随机方向

天牛在搜寻食物的过程中，前进的方向是随机的，左右两须所指方向也具备不确定性，则其前进方向向量可以表示为：

(1)

式中，n为空间维数;rand(·)为随机方向。

② 确定天牛左右须的空间坐标

通过天牛觅食的行为来模仿天牛触须情况以确定左右须坐标，表示为：

(2)

式中，xl为左须指定坐标；xr为右须指定坐标；xt为在迭代第t次时天牛所处的具体位置；Lt为第t次迭代时天牛两须之间的距离。

③ 选定适应度函数表达式

(3)

式中，f(·)为适应度函数；fl，fr分别为天牛的左、右两须的适应度函数，对于待优化的函数值f，判断左右两须的值的大小：

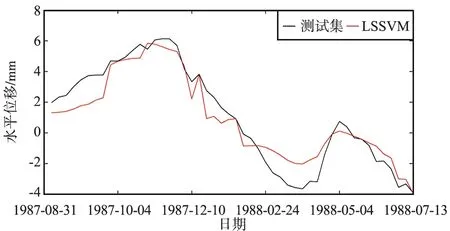
若fl

若fl>fr，则天牛朝着右须的方向前进距离s，即x=x-s×normal(xl-xr)。

综上情况，可以将以上2种情况采用符号函数sign统一写成：

x=x-s×normal(xl-xr)×sign(fl-fr)，

(4)

式中，normal为归一化函数，可进一步表示为:

x=x-s×a×sign(fl-fr)。

(5)

④ 确定下一次迭代时天牛的前进距离及方向

在迭代搜寻的过程中，步长随着迭代次数的增加也在随之改变，从而确保最大范围搜索到气味浓度最大的食物的位置，可以表示为：

xt=xt-1+st×a×sign(fl-fr)，

(6)

式中，st为迭代第t次的步长。

天牛在搜寻食物的过程中，天牛的行进步长s与两须之间的距离L0之间的比值是个固定常数，即：

s=c×L0，

(7)

式中，c为步长因子，c∈[0,1]，通常可取c=0.95，则：

st=0.95×st-1+0.01。

(8)

在天牛算法寻优的过程中，刚开始，为保证全局范围内寻优，避免陷入局部最优，搜索步长应足够大，在搜索寻优后期，随着迭代次数的增加，步长将随之逐步减小。为提高算法的收敛速度，当迭代第i次的适应度值fi小于当前的最佳适度值fm，步长调节机制可以改进如下：

(9)

式中，θ∈[0,2]，为随机选取的常数。当fi大于历史最佳适度值fm时，则步长因子为c，否则，步长因子为g。通过不断减小步长因子来提高算法寻优的收敛速度，使适应度值逐渐稳定于最佳值。

2 随机森林算法

RF算法是Breiman等提出的一种由Bagging和分类回归树(Classification and Regression Tree,CART)相结合的分类回归模型[10]。在训练集中利用bootstrap重抽样技术来随机抽取样本集，其中决策树是通过二分递归分割技术将样本集进行一分为二的分割，引入袋装法和特征子空间法来对训练样本集进行抽样，在促进决策树生长的过程中，毫无约束、最大限度地成长，最终多棵决策树组成RF分类器，对数据训练集进行分类预测，将预测均值作为最终预测结果[11]。弥补决策树单一分类器所存在的易陷入局部最优及预测结果存在偶然性的缺陷。

2.1 CART决策树

在RF算法中，各个单一决策树之间毫无关联，独立存在，所以分节点处的特征值均是随机抽取的[12]。在决策树分枝的过程中，主要是通过最小信息化原则依据每个子节点上的基尼不纯度平均减小值来划分出最佳分类特征，依次分枝形成下一个子节点，最终建立无约束的回归模型树。针对分类问题，CART使用基尼指数(Gini)作为评判标准，若有n棵树，则：

(10)

式中，Gini为基尼指数；i为特征分类数量；Pi为目前特征类别的概率；1-Pi为特征样本特征归类错误的概率。由式(10)可以看出，特征分类越平均，Gini的值越大；分类越不均匀，Gini值越小。

对于回归问题，在n个节点分枝成为2个节点之后，Gini将趋近于最小化，则该特征值对应的Gini为：

|Gini|=min[min∑(wi-b1)2+∑(wi-b2)2],

(11)

式中，在分枝为2个节点处的样本集y1,y2中，wi为输入样本；b1,b2分别为2个样本的输出均值。

2.2 参数的选取

在利用RF建模的过程中，尽管算法会受到众多参数的影响，但其中能够决定模型预测精度及稳定性的主要参数是决策树的个数和分裂属性个数，常用ntree和mtry表示。ntree的值越大，预测过拟合的效果越小，一般不小于100。mtry是指决策树在进行分裂时所生成的节点数量，其值越大，则子模型间的差异越小[13]。目前,常规RF算法中常利用人工经验、网格搜索的方法进行RF参数的标定，所提供的参数在训练过程中难以达到拟合结果最佳的效果。引入BAS算法来进行RF模型参数调优，进一步来提高RF模型的预测精度。

2.3 BAS-RF预测模型构建

由混凝土大坝结构成因分析，大坝产生水平位移主要受温度、水压和时效的影响，从而产生变形、裂缝、滑动力和渗流等现象[14]。这些因素之间呈现出非线性关系，传统的预测模型有时会受到多重共线性的影响，最终的预测效果难以达到实际工程的要求[15]。本文提出利用RF方法来解决多重变量间的交互作用，考虑到RF算法的预测精度受到决策树个数和分类属性个数的影响，进而引入天牛寻优算法进行参数优化，最终利用BAS-RF组合算法来构建大坝水平位移预测模型，具体步骤如下：

① 利用统计学方法对收集的大坝水平位移监测数据进行初步处理，剔除存有缺陷的数据，保证参与实验数据的可靠性，并将数据集分为训练集和测试集，进行归一化；

② 初始化BAS算法的参数，设定步长因子、最大迭代次数和天牛的初始位置；

③ 选定BAS参数优化中的适应度函数，分析理解ntree，mtry与均方根误差之间的函数关系来构建BAS算法的适应度函数,具体如下：

(12)

④ 确定天牛初始的位置，首先需要计算出天牛左右须的适应度函数值f(xl)和f(xr)，比较保留记录最佳函数值的天牛位置；

⑤ 更新迭代天牛的位置，对左右须收集到的气味浓度进行比较，获取最佳食物气味浓度的传播方向，选定前进方向的步长值，计算出天牛下一次所到达的位置；

⑥ 根据设定的最大迭代次数或预先设定的适应函数值的理想精度是否达到，判断之后的操作，若满足要求，则参数输出进行下一步，否则重新迭代更新天牛位置,继续参数寻优过程；

⑦ 获取迭代结束输出的最佳参数值，将其带入RF预测模型中，计算输出预测值，进行精度评定分析。具体的操作流程如图2所示。

图2 BAS-RF预测模型流程Fig.2 BAS-RF prediction model flowchart

3 实验分析

3.1 数据来源

本文数据选择的是丰满大坝30号坝段1985年1月—1988年7月的坝顶水平位移及同期温度、时效以及库水位的监测数据[16]。丰满大坝坝顶全长1 080 m，其中最大的坝高91.7 m，坝顶高程加固后为267.7 m。大坝共有60个坝段，左右两边有37个坝段，11个溢流坝段，11个厂房取水坝段和1个过渡坝段，每个坝段的长度均为18 m，最大坝基宽度65 m，坝顶宽度9.0～13.5 m。将所选用的30号坝的200组监测数据中的150组作为训练样本集用于预测模型建立，50组数据作为训练模型的检测。大坝水平位移序列如图3所示。

图3 大坝水平位移序列Fig.3 Horizontal displacement sequence of the dam

大坝水平位移变形主要受温度、时效和水压的影响，即：

δ=δθ+δT+δH，

(13)

式中，δθ为时效分量；δT为温度分量；δH为水压分量。

根据文献[17]通过属性约简和重要性评价结果选定时效分量(θ，lnθ)，温度分量(sin(2πt/365)，sin(4πt/365)，cos(2πt/365)，cos(4πt/365))和水压分量(H,H2,H3)，共9项影响因子作为输入量，大坝水平位移作为输出值。

针对RF算法中参数的选择，传统RF算法中选用网格搜索法来寻找ntree和mtry两个参数，最终的预测效果往往难以达到理想值。本文引入BAS算法来进行参数优化,建立大坝水平位移预测模型，相较于常规方法，预测结果更为稳定。

3.2 网格搜索寻参

网格搜索算法(Grid Search Algorithm，GSM)是一种通过遍历给定的参数组合来优化模型表现的方法，是常规RF算法中寻找参数的常用方法[18]。其将所有参数可能存在的值进行排列分组，并将所有的组合利用网格的形式呈现出来，全部用于RF模型的参数值，利用训练数据构建模型，选出预测效果最优的模型所对应的参数值即为所寻找的最适参数值[19]。对于RF算法中的ntree和mtry两个参数，分别将其寻优区间设置为[10,800]和[1,15],且寻优间隔为4和1，选择均方根误差作为评判的目标函数，从而获取RF算法中的参数值。

3.3 天牛搜索寻参

在利用BAS算法进行优化寻参时，最大迭代次数设置为100，维数为2，天牛初始步长为1，步长衰减因子为0.95，且确定ntree，mtry和均方根误差值间的函数关系，设定两参数的取值区间分别为[10,800]和[1,15]。通过选定的训练数据集通过BAS算法优化迭代选定出最优解,如图4所示。当迭代次数达到15之后，目标函数达到最小值，此时的均方根误差为0.534 mm。

图4 天牛迭代寻参Fig.4 Longhorn beetles iterative search for parameters

3.4 预测精度分析

为了验证BAS-RF预测模型的优越性，本实验分别利用BP，LSSVM，RF及BAS-RF四种方法来建立大坝水平位移预测模型，其中通过GSM和天牛搜寻算法为RF算法建模所提供的参数分别为(171,1)和(155,1)，2种算法最终选定的参数相差不大，但GSM在寻参的过程中迭代的次数为1 213，寻参时长要远远大于天牛搜索算法，表明天牛搜索算法收敛速度更快。在4种方法建立大坝水平位移预测模型后，将选定的测试集输入各个预测模型进行精度检验，获取其预测曲线，如图5～图8所示。

图5 RF建模预测结果Fig.5 RF modeling prediction results

图6 BP建模预测结果Fig.6 BP modeling prediction results

图7 LSSVM建模预测结果Fig.7 LSSVM modeling prediction results

图8 BAS-RF建模预测结果Fig.8 BAS-RF modeling prediction results

利用150组训练集数据建立水平位移预测模型，并通过50组测试集数据进行检测，获得4种预测模型的大坝水平位移预测曲线图。其中,利用BP神经网络法所构建模型的预测值与检测值间的曲线吻合度最低，表明传统BP神经算法构建预测模型的稳定性仍需进一步提升。相比于BP神经网络算法、LSSVM和RF三种方法，BAS-RF组合算法构建的大坝水平位移预测模型的曲线走势与测试集曲线图最为接近，相差最小。为更加清晰地展现4种模型预测结果与真值间误差的变化及整体波动范围，绘制出模型预测误差变化曲线，如图9所示。

图9 4种方法的残差结果Fig.9 Residual results of the four methods

由图9可以看出，4种预测模型的拟合误差曲线的波动范围均为-3～3 mm，拟合效果较为理想。相较于BP神经网络预测模型，LSSVM预测模型与RF预测模型的误差变化范围较为接近，其波动范围要略小于BP神经网络。而通过天牛须算法优化后的RF算法构建预测模型的误差范围最小，大致处于-1～1 mm，其预测精度明显要优于其他3种预测模型，稳定性相较于常规RF也得到提升。为了进一步比较分析4种预测模型的预测精度，分别计算出各个模型预测结果的误差变化区间、均方差、均方根误差和平均绝对误差来作为模型预测精度的评定参数，如表1所示。

表1 4种模型预测精度统计

由表1可以看出，相比于其他3种预测模型，BP神经网络模型的预测结果误差变化区间为[-2.274,2.075]，波动范围较大，且均方根误差为1.086 mm，要明显大于RF和LSSVM所构建的预测模型，说明传统BP神经网络构建预测模型的稳定性及精确度需要进一步提高。RF算法和LSSVM算法建模的预测误差区间、均方差等比较接近，其模型预测效果也较为理想，但精度不高，结合图5和图7可知，二者局部范围波动较大，误差值也随之明显变大，可能出现了局部最优的问题。经过BAS优化后的RF能够提高收敛速度，且避免在后期迭代的过程中陷入局部最优，能够全局搜索参数最优值，从而提高模型大坝水平位移预测精度。因此BAS-RF能够较好地处理大坝水平位移与影响因子之间的非线性关系，具有一定的适用性。