高精度室内融合定位算法研究
2022-09-09杨国伟胡起立毕美华
黄 健,杨国伟*,胡起立,毕美华,李 晶,李 娜
(1.杭州电子科技大学 通信工程学院,浙江 杭州 310018;2.杭州海关技术中心 环境与化学安全检测研究所,浙江 杭州 311200;3.中国电子科技集团公司航天信息应用技术重点实验室,河北 石家庄 050081)
0 引言
近年来,随着无线通信技术的迅速发展,基于位置的服务在各个领域中都爆发出急速增长的需求,精确定位技术开始广泛地应用于各个领域。室内定位作为导航定位的“最后一公里”,一直是研究机构和企业关注的热点[1]。近十多年来,大量的新兴技术如地磁、WiFi、蓝牙、射频识别、可见光[2-3]和超声波等相继应用于室内定位,但是这些技术都有各自的局限性,很难实现在实际复杂多变场景中的高精度定位。近年来,超宽带(Ultra-Wideband,UWB)技术因具有很高的分辨率和很强的抗多径能力能实现高精度测距而受到广泛关注。
事实上,在非视距(Non-Line-of-Sight,NLOS)室内环境中,由于障碍物的遮挡会导致UWB定位精度急速下降,因此单一的室内定位方式仍然难以在复杂的室内环境中实现稳定且高精度的定位。惯性导航技术作为自主导航技术[4],可以辅助UWB技术渡过NLOS的室内环境。又由于低成本的微机电系统(MEMS)惯性传感器的精度难以匹配传统惯性导航算法,所以需要采用行人航位推算(Pedestrian Dead Reckoning,PDR)算法来代替传统的积分方法。但MEMS惯性传感器的误差随着系统运行时间增加,会出现较大的误差累积情况。为解决单一定位技术在室内定位时的不足,众多学者提出采用融合定位方式完成室内定位。文献[5]实现了WiFi与惯导结合的室内定位系统,但定位精度仍相对较低。文献[6]将惯导定位与地图结合实现手机端的室内定位,但是要求正常持握手机姿态,实用性不好。文献[7]对WiFi和PDR室内组合定位进行了研究,通过无迹卡尔曼滤波算法融合二者定位数据,但定位精度仍受限于WiFi定位精度。文献[8]使用扩展卡尔曼滤波融合UWB和PDR数据,但无法校准航向角误差。
本文基于融合定位的思想,充分利用UWB和PDR各自的优势,提出一种基于UWB与PDR的新型融合定位方法。在NLOS环境中,UWB定位产生了较大误差甚至无法定位时,借助PDR减少因为NLOS而产生的定位误差,同时可以借助UWB高精度的定位信息来消除PDR误差累积。本文重点聚焦了二者融合定位过程中的主辅切换方法和补偿方法,实验证明本文方法的定位轨迹更加贴近真实轨迹,有效地降低了NLOS定位误差,提高了室内定位的性能。
1 UWB定位模型
1.1 UWB测距原理
本文UWB测距采用简单高效的TOA技术方案[9]。由于基于TOA的测距通常需要基站与标签之间时间同步,而精确的时间同步实现难度大。UWB测距首先采用了单侧双向测距(SS-TWR),该方法通过信号在标签与基站之间的来回传输,避免了标签与基站之间的时间同步问题,测距流程如图1所示。
(1)
该SS-TWR方法没有标签与基站的时间同步问题。但是,由于标签与基站之间存在微小的时钟偏移,如果标签和基站的时钟偏移分别为eA和eB,则飞行时间误差为:
(2)
由式(2)可以看出,飞行时间的误差随着Treply增加而增加,并且同设备的时钟偏移也有关系。所以SS-TWR的精度也不够高,因此提出了一种改进双向测距法——双边双向测距(ADS-TWR)[10]。
ADS-TWR方法是SS-TWR的升级改进版本,测距流程如图2所示。

图2 ADS-TWR测距流程Fig.2 ADS-TWR ranging process
(3)
误差分析如下:
(4)
由式(4)可以看出,ADS-TWR的误差与延迟时间Treply无关。同样的时钟差,ADS-TWR比SS-TWR的误差小很多,可以得到更高的测距精度。获得测距距离后,由于UWB模块出厂时天线就存在接收信号延迟的问题,对UWB模块进行测距修正,以提高实际使用中的测距精度。
1.2 UWB定位与天牛须搜索算法
在无线传感器网络定位算法中,全局搜索算法越来越受到关注。全局搜索算法将寻常三维定位的非线性方程组求解问题转化为最优化问题,在很多领域得到成功应用[11],本文尝试将天牛须搜索(Beetle Antennae Search,BAS)算法应用到UWB定位算法中。

(5)
(6)

st=cδt,
(7)
δt=ηδt-1,
(8)
下标r,l表示右侧和左侧;上标t表示第t次迭代;δ为天牛的步长;c为质心到须的距离与步长之间的系数;η为步长衰减系数。天牛在t时刻的坐标为:
(9)
式中,sign(·)为符号函数。BAS算法的整体流程如下:
① 设置算法的迭代次数、初始步长和步长的衰减系数,并随机生成天牛的初始位置。
② 随机生成单位向量b,根据式(5)和式(6)计算天牛左须和右须的坐标和适应度函数,沿着较好方向前进,并更新下一次迭代使用的搜索范围和步长。
③ 根据式(9),经过迭代不断更新天牛的空间坐标并更新最佳值。
④ 判断是否达到最大迭代次数或全局最优解的适应值是否满足最小界限,若未达到转到步骤②。
将BAS算法应用到UWB定位的关键就是设置适应度函数(食物气味强度)。f(x)为本文设计的适应度函数,表示为:
(10)

2 PDR模型
PDR算法是惯性导航的一种简化算法,在惯性传感器精度不高时,利用人走动产生周期性变化的特点,估计出人行走的步数和步长,再获得每一步的航向角即可以求解出人行走前后的相对位置。PDR定位原理如图3所示。

图3 PDR定位原理Fig.3 PDR positioning principle
若(xk,yk)为人的当前位置,Lk为估计的步长,ψk为行走的航向角,则行人下一步的位置(xk+1,yk+1)可以通过下式求出:
(11)
PDR算法需要知道开始第一步的具体位置和方向,由此推算出后面行走的相对位置。所以步态检测、步长估计和航向估计是PDR算法的3个核心步骤。
2.1 步态检测
因为伪波峰的存在,传统的基于阈值峰值检测法会出现漏检或误检的情况,本文采用了一种基于时间周期性的峰值检测法作为步态检测的方法[13]。当人在行走时,每一步都可以看成一个周期,并且每一步相隔的时间都应该差不多,所以可以利用该特点并结合峰值检测法来进行步态检测。
首先,通过传统的波峰检测法求得第1个波峰与第2个波峰相隔的时间,记为t1,根据加速度的周期性变化原理,第2个波峰与第3个波峰之间的相隔时间也大概为t1,因此可以在第2个波峰之后的t1时间附近寻找第3个波峰,找到第3个波峰之后更新相隔时间,以此类推找到所有波峰点。计算如下:
(12)

(13)
式中,δ为波动参数,可由实验测试进行估计。为了保证每一步的周期具有强的相关性,每一步后要对Ti进行更新。最后,由于伪波峰的影响,经过筛选,在波动范围内产生多个极值点,取这几个极值点中波峰最大的点作为真正的波峰点。
2.2 步长估计
获得步数后,要估计对应每一步的长度。因为每个人的生理状况不一样,步长也因人而异。当然,同一个人在行走过程中,每一步长度也有所不同,所以基于常数模型的步长估计很难适应实际情况。本文的自适应算法结合了基于加速度幅值变化非线性步长估计[14]和基于步频的线性步长估计[15],计算如下:
(14)
式中,α,β与人的生理因素有关,可由大量实验得出,α取值在0.4~0.5,β取值在0~0.1;amax,amin分别表示该步周期内加速度的最大值和最小值;fk为对应的每一步的行走频率;φ是一个常数。
由于噪声的影响,加速度数据会引入噪声误差,所以要对采集的加速度数据进行滤波来消除噪声,提高步态检测的准确率。本文使用滑动平均滤波来降低噪声信息。采用上述的步态检测法和步长模型,并使用陀螺仪计算得到前进的航向角改变量,根据UWB前期准确定位的结果得到初始值,再通过式(11)就可以得到航位推算位置。
3 UWB和PDR融合定位
3.1 UWB NLOS定位场景判定和优化


(15)
由于滤波器的递推作用,受NLOS污染严重而偏差较大的坐标值不仅使当前时刻的坐标值估计发生较大偏差,并且由于卡尔曼滤波器的记忆性,使后续的坐标估计都受到严重影响,对于这些不准确的坐标点,应当舍弃。在被舍弃的点上,用状态预测值代替状态估计值,所以本文引入偏移卡尔曼滤波器消除NLOS误差[17]。当滤波过程中没有进入NLOS场景,卡尔曼滤波则正常迭代;若进入NLOS场景,通过把卡尔曼增益设为0来舍去这个测量值,并用状态预测值来代替状态估计值。x轴定位数据的卡尔曼滤波如图4所示,当沿着y轴方向运动时,坐标x轴数据变化较小,门限值选取合理,该方法对x轴坐标NLOS误差抑制明显。
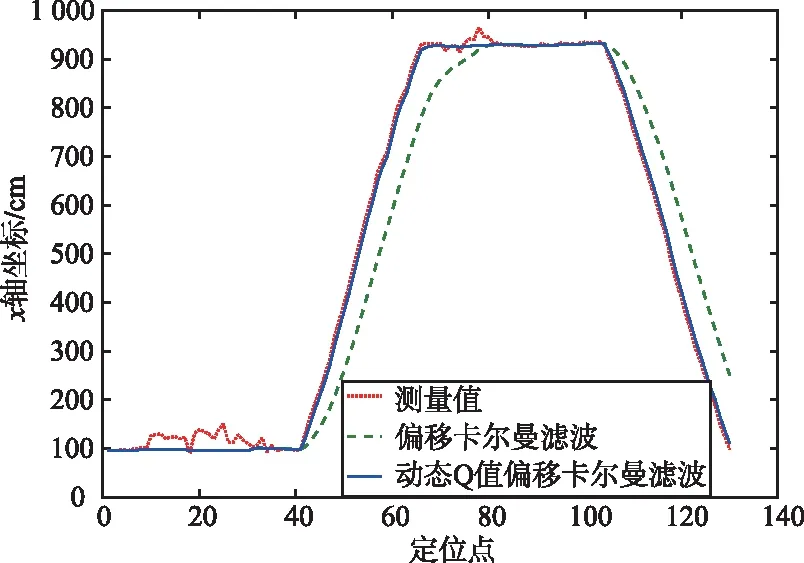
图4 x轴定位数据的卡尔曼滤波Fig.4 Kalman filter of x-axis positioning data
但是当运动方向改变,沿着x轴方向运动时,滤波模型发生变化,若滤波器的参数保持不变,x轴数据变化过快时,将影响正常滤波,严重时甚至造成滤波发散,这时必须改变滤波器参数增强滤波收敛效果。数据急速变化时,可以通过增加过程噪声Q值,Q值越大,代表越信任实际测量值,以提高此段的跟踪能力,从而促使该段估计值能较快收敛,但Q值也不能太大,当Q值太大时滤波数据将基本与实际测量值相等,无法做残差判断。由图4可以看出,改变了Q值的偏移卡尔曼滤波能更好地适应数据急速变化的情况。只通过x轴的残差数据Δdx来判断NLOS场景是不够的,对y轴数据也做相同处理得到残差数据Δdy,对二者做联合判断,2个残差值只要有一个大于阈值ε就可以判定进入NLOS场景。
通过滤波器来更好地获取运动方向的变化,其关键是需要实现动态地取Q值。可以利用PDR的航向角来辅助滤波器动态地取Q值。PDR定位是一种相对定位方法,开始定位时需要获得PDR的初始坐标点和初始航向角。PDR的初始位置可由UWB定位的坐标获得,PDR航向角初始值由初始时刻UWB的N个准确定位结果的位置共同决定。如果只选用UWB的2个定位结果获得的初始航向角,初始航向角有时会因为定位的波动产生较大的误差。因为UWB数据获取频率通常是大于PDR每一步的频率,所以在PDR进行第一步定位前有N个UWB定位数据。对这N个数据做线性拟合[18],得到的直线斜率作为PDR初始航向角,减少定位波动对初始航向角的影响。N的值由实际UWB的采样频率和实际场景决定,本文N值取4。获得PDR的初始坐标和初始航向角后,就可以获得PDR每一步的坐标和航向角,知道大概的运动方向。考虑x轴坐标为滤波对象,当PDR的航向角与x轴的夹角在90°附近时,数据变动较小,这时Q值可以取较小的值。当PDR的航向角与x轴的夹角在45°附近时,数据变动较平缓,这时Q值可以取适中的值;当PDR的航向角与x轴的夹角在0°附近时,数据变动较大,这时Q值可以取较大的值。当滤波对象为y轴坐标时,方法同上。所以,可以根据PDR的航向角值θ来动态地对Q赋值。本文通过给定的3个Q值:Q1,Q2和Q3,来覆盖整个角度范围(0°,360°)。Q1,Q2,Q3值根据实际数据和滤波情况来确定,本文设置的滤波器R=0.542,Q1=1,Q2=0.4,Q3=0.05,则有:
(16)
式中,QX为x轴坐标滤波器Q值;QY为y轴坐标滤波器Q值。
3.2 PDR误差累积修正和融合定位
由于PDR定位存在累积误差,特别是较大角度的拐弯会对PDR航向角造成较大的影响。UWB是一种绝对定位方式,可以通过UWB定位对PDR的航向角进行修正[19-20]。首先,设定航向角变化阈值H,当某一步相较于初始航向角的航向角变化超过阈值H时,认为PDR航向角累积误差过大,对这一步的PDR定位进行UWB定位替代,用UWB估计的方向取代PDR的当前航向,用UWB定位坐标作为PDR的初始坐标。若UWB定位刚好处于NLOS场景,先不修正,等到UWB定位离开NLOS场景时,再对PDR定位进行修正。
获得UWB优化后的定位数据、NLOS情况和误差累积修正的PDR数据后,要对二者数据进行融合。在LOS场景,直接以UWB滤波优化后的定位数据作为定位结果;在NLOS场景,UWB定位数据会有较大的误差,因此舍弃UWB定位数据,以误差累积修正后的PDR的定位数据代替在NLOS场景中UWB的定位数据,将PDR定位数据作为NLOS场景中的定位结果。
4 实验结果与分析
4.1 UWB定位测试
测试在2个场景进行:一个是杭州电子科技大学1教428教室,该场景无遮挡,不存在NLOS情况;另一个是杭州电子科技大学1教架空层,遮挡场景多,存在NLOS情况。测试设备包括4个UWB基站和1个自主设计的高精度定位系统,该系统包括用于UWB定位的DW1000模块和用于PDR定位的MPU9250惯导模块,实验测试数据通过4G模块上传到云端。测试设备及测试环境如图5所示。

(a) 定位装置

(b) UWB基站

(c) 教室场景

(d) 架空层车库场景
进行定位实验前,首先对UWB模块进行测距修正。在LOS环境下测距误差可以通过调整UWB模块的天线延时参数来降低。在LOS环境下,以0.6 m的间隔获得各个点的测距值,再利用最小二乘法求得一个修正值,使各个点修正后的测距值与真实距离值的差值平方和最小,最后将该修正值除以光速转换成天线延时参数输入到UWB模块中。测距修正前后数据如表1所示。测距修正前,平均测距误差为21.19 cm;测距修正后,平均测距误差约为3.9 cm。

表1 UWB测距值
在教室场景中布置的4个UWB基站坐标分别为(0,0,2.4),(9.25,0,2.4),(8.95,11.7,2.4),(-0.1,11.5,2.4),在车库场景中布置的UWB基站坐标分别为(0,0,1.8),(16.8,0,1.8),(16.8,25.2,1.8),(0,25.2,1.8),接着选定几个测试坐标进行自主设计定位系统的UWB定位测试,分别用测距未修正最小二乘法算法、测距修正最小二乘法算法和测距修正BAS算法进行定位并对结果进行比较。因为测距精度的限制,UWB定位的z轴定位误差较大,所以通常UWB定位只关注x轴和y轴的定位精度,本实验UWB定位也只考虑了x轴和y轴的二维平面定位精度,并以定位坐标与真实坐标的欧式距离来衡量定位精度,定位结果如图6所示。

(a) 教室定位示例
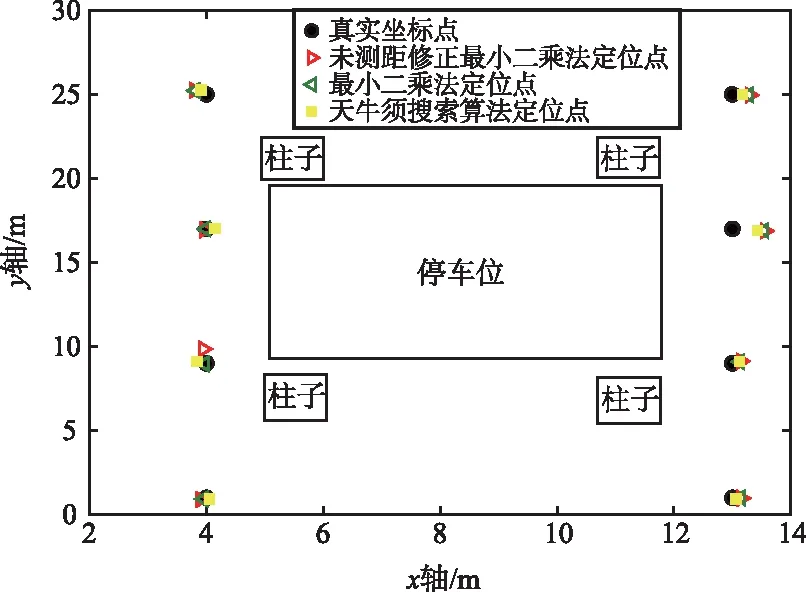
(b) 架空层定位示例
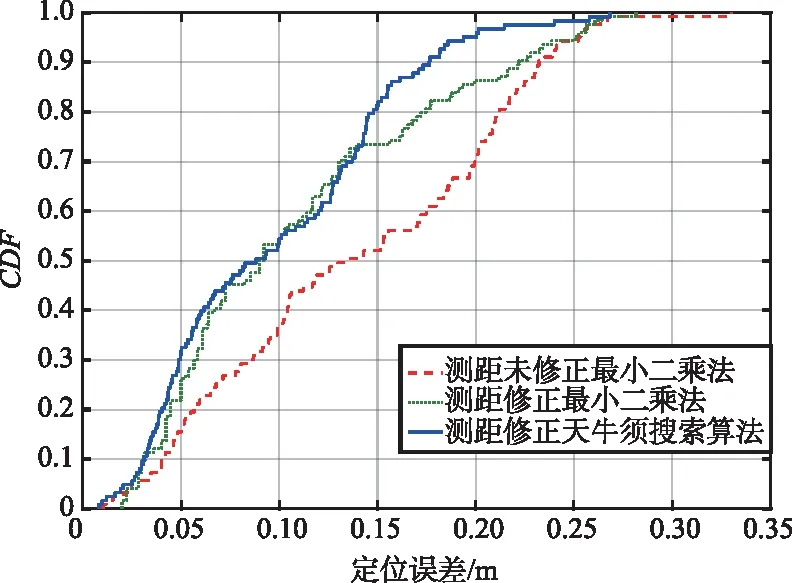
(c) 定位误差累积分布函数(CDF)
在教室场景中,测距未修正最小二乘法的平均定位误差约为13.79 cm,测距修正最小二乘法的平均定位误差约为10.96 cm,而测距修正BAS算法的平均定位误差约为9.65 cm。在地下车库场景中,测距未修正最小二乘法的平均定位误差约为22.05 cm,测距修正最小二乘法的平均定位误差约为19.63 cm,而测距修正BAS算法的平均定位误差约为16.65 cm。可见,在场景遮挡情况少、定位结果较好的情况下,BAS算法虽然也提升了定位精度,但是提升不大。而在场景遮挡情况严重、定位结果较差的情况下,该优化算法的提升效果较好。
4.2 PDR定位测试
首先对本文PDR算法的步态检测和步长估计进行评估。进行步态检测评估时,分别走了20,50,100步,再用基于阈值的峰值检测法和基于时间周期性的峰值检测法进行比较,实验结果如图7所示。由图7可以看出,基于时间周期性的峰值检测法相较于基于阈值的峰值检测法精度更高,提升了约5%的精度。进行步长估计评估时,控制每一步的步长都保持在60 cm,再用本文的自适应步长估计算法同经典的基于加速度幅值变化非线性步长估计进行对比,实验结果如图7(d)所示,可以看出本文的自适应步长估计算法精度更高。

(a) 真实步数为20

(b) 真实步数为50

(c) 真实步数为100

(d) 步长误差分布
PDR实验在杭州电子科技大学1教的架空层车库进行测试,设定起点坐标为(0,0),沿着(0,0),(0,25.3),(-8.3,25.5),(-8.3,0),(0,0)的路线行走,通过定位系统上惯性传感器模块的数据采集,对数据进行处理,再用本文的PDR算法进行轨迹计算,实验结果如图8所示。可以看出,在开始阶段PDR定位能达到较高的精度,定位误差能保持在20 cm以内。随着时间的推移,由于误差累积,特别是拐角的影响,定位误差逐渐增大,最后的定位点与实际点的误差达到74 cm,所以PDR单独定位时适合短时间且拐弯较少的场景。

图8 PDR定位实验结果Fig.8 Diagram of PDR positioning test
4.3 UWB和PDR融合定位
融合定位实验在杭州电子科技大学1教的架空层车库进行测试。测试场景如图9所示,中间有2根柱子作为遮挡来创造NLOS环境。

图9 融合定位测试场景Fig.9 Environment of fusion positioning test
首先布置4个UWB基站,其坐标分别为(0,0,1.8),(0.4,16.9,1.8),(9.3,0.05,1.8),(8,16.25,1.8),并设定起点坐标为(1,1)。沿着(1,1),(1,14),(9.3,14),(9.3,1),(1,1)的路线行走,同时开启UWB和PDR定位,UWB定位采用上述的BAS算法,PDR定位采用上述的PDR算法,并对二者的定位进行数据融合。本文的融合算法针对UWB NLOS区域,在LOS区域仍采用UWB定位,定位结果如图10所示。由图10可以看出,由于柱子遮挡的影响,UWB定位在2个NLOS处产生了较大的定位误差,PDR定位在刚开始时误差也较小,但是经过了2次90°拐弯,航向角产生了约5%的偏移,本文融合定位算法的定位轨迹误差更小,也更接近实际真实轨迹。本文各种定位方式的误差如下:在NLOS场景中,UWB的平均定位误差为42.8 cm,PDR的平均定位误差为17.2 cm,融合定位的误差为13.7 cm。本文的融合算法较好地利用了2个系统各自的特点,有效地抑制了NLOS干扰,提高室内定位整体准确性和可靠性。

图10 UWB和PDR融合定位实验结果Fig.10 UWB and PDR fusion positioning experiment
5 结束语
本文对UWB和PDR室内定位算法进行独立和融合的改进研究。首先将BAS算法应用到UWB定位中,在无遮挡和有遮挡情况下开展定位实验测试,精度分别提升至9.65,16.65 cm。然后将基于时间的周期性的峰值检测法和自适应步长估计应用到PDR定位算法中,实验测试结果显示,在最初30 m以内和一个拐弯的情况,精度在20 cm左右,但随着距离增加和拐弯增多,精度下降较快。尽管上述2种改进方法都在一定情况下提升了各自定位精度,但仍无法解决UWB定位NLOS和PDR定位累计误差的问题。针对这2个问题,提出了一种基于UWB和PDR技术的融合定位算法,根据基于PDR航向角动态改变过程噪声Q值的偏移卡尔曼滤波法来判别NLOS情况,利用了UWB定位修正PDR累积误差,同时利用了PDR定位修正UWB在NLOS下的定位误差。实验测试结果显示,所提出的融合定位算法有效地降低了NLOS情况下UWB的定位误差,平均定位误差降至0.137 m,比单一UWB定位精度提升了约68%,对于地下停车场、仓库和商场等大型室内场所的长时间、高精度定位具有一定的参考价值。
