改进调节因子的GPS/SINS组合导航自适应滤波算法*

孙淑光 陈建达

中国民航大学电子信息与自动化学院，天津 300300

0 引言

随着微机电系统(MEMS)技术的发展，集陀螺仪和加速度计于一体的微惯性测量单元(MIMU)在导航领域得到广泛应用。受价格因素制约，低成本传感器导航方式成为无人机市场中主要的应用需求。

捷联式惯性导航系统(SINS)短期导航时间内精度较高，但存在定位误差随时间积累的固有缺点[1]。全球定位系统(GPS)可以全天候、连续地提供精确的位置、速度信息，但动态响应能力较差，信号受遮挡效应和多路径效应干扰明显[2]，在高动态复杂环境中单独依赖GPS定位往往会出现导航短暂不可用的情况。无人机通常在山区林地运行，环境复杂，飞行过程机动性大，且要求设备成本低廉。因此，现代无人机多采用GPS/SINS组合导航的形式，通过优势互补，在提高导航定位精度的同时,确保系统的鲁棒性和稳定性。

传统的组合导航方式通常采用卡尔曼滤波作为数据融合的方法，综合系统状态估计信息和量测信息，通过滤波算法获取最优估计。传统卡尔曼滤波将传感器误差特性描述为静态白噪声，但实际上，随着运行时间及工作环境的变化，传感器噪声的数学统计特性(均值、方差)是时变的，基于静态特征的噪声表征方式不能很好地反映目标传感器的噪声特性[3]。在高动态运行情况下，会导致无人机滤波不稳定，甚至产生发散现象。针对这一问题，一些自适应滤波算法应运而生。

文献[4]通过调整不同定位精度下GNSS测量的噪声协方差，并基于机器学习和模糊逻辑[5]方法获得相比于传统卡尔曼滤波更好的定位精度。文献[6]采用三段式方法评估自适应比例因子，与其它现有算法相比，其在静态和动态条件下均能有效减少漂移和随机噪声带来的影响。文献[7]为提高MEMS陀螺仪的估计性能，提出一种加权鲁棒Sage-Husa自适应滤波算法。该算法利用一种基于残差估计的方法，减少了异常值对角速度估计的影响。文献[8]提出了一种基于滑动衰减因子的Sage-Husa自适应组合导航算法。该算法根据量测噪声统计特性的变化，选择合适的衰减因子，以适应实际噪声变化带来的影响。

上述文献通过不同的改进方法提高了组合导航系统的整体性能，为了进一步提高无人机在运行中的自适应性，本文提出一种基于速度信息改进调节因子γ的Sage-Husa自适应滤波方法。该算法可以克服传统卡尔曼滤波在高动态条件下滤波不稳定的缺陷，增强组合导航算法的自适应性，提高定位精度。

1 GPS/SINS组合导航系统建模

1.1 组合导航整体架构

无人机组合导航系统采用包含三轴陀螺仪和三轴加速度计MIMU模块和GPS接收模块的集成传感元件，通过组合导航算法进行数据融合，整体分为惯性导航模块、GPS模块以及数据融合模块3部分。具体方案如图1所示。

图1 无人机组合导航方案

由图1可知，首先利用经过初始误差补偿的惯性测量元件数据进行惯性导航解算，利用GPS模块解算无人机的位置与速度信息，同时将GPS速度信息作为滤波算法中调节因子计算的要素，将GPS、SINS输出的导航信息利用改进的Sage-Husa自适应滤波算法进行数据融合，以获取高精度定位信息。

1.2 惯性传感器误差方程

陀螺仪与加速度计分别为载体的角运动与线运动测量元件，两者本身存在误差且误差存在方式相似，主要包括常值误差以及白噪声误差。陀螺组件模型表示为：

(1)

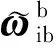
εb=εb+wg

(2)

式中，εb为常值漂移，wg为白噪声误差。

加速度计组件模型表示为：

(3)

(4)

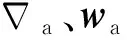
1.3 GPS/SINS组合导航方程

1.3.1 状态方程

组合导航系统的状态方程参量选择SINS的位置误差、速度误差、姿态角误差、陀螺仪漂移误差及加速度计零偏误差。误差状态向量为：

X=[X1X2X3X4X5]T

(5)

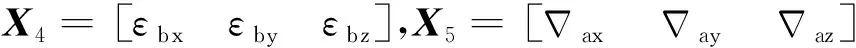
系统状态方程表示为：

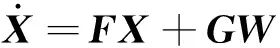
(6)

位置误差微分方程表示为：

(7)

(8)

(9)

速度误差微分方程表示为：

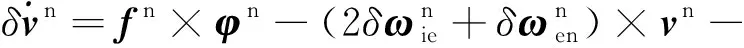
(10)

式中，fn为导航坐标系中的比力信息。

姿态误差角微分方程表示为：

(11)

(12)

(13)

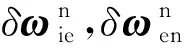
F为系统状态转移矩阵，表达式为：

(14)

式中，Fω为误差状态转移矩阵，由系统状态变量的微分方程推导得到

(15)

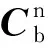
G为噪声分配矩阵，表达式为：

(16)

W为系统噪声，表达式为：

W=[ωgxωgyωgzωaxωayωaz]T

(17)

式中，ωgx,ωgy,ωgz为陀螺仪白噪声；ωax,ωay,ωaz为加速度计白噪声。

1.3.2 量测方程

SINS解算出的位置为(LI,λI,hI)，速度为(veI,vnI,vuI)，GPS计算出的位置为(LG,λG,hG)，速度为(veG,vnG,vuG)。量测方程表示为：

(18)

式中：

(19)

量测噪声矩阵V可表示为：

(20)

1.4 改进的Sage-Husa自适应滤波

传统卡尔曼滤波主要适用于线性系统，常用离散化模型来进行系统实现，需对状态方程和量测方程进行离散化处理，处理后可得：

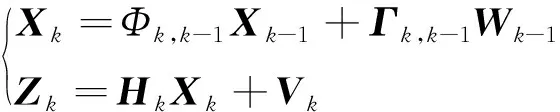
(21)

式中，Φk,k-1表示离散系统状态一步转移矩阵；Γk-1表示离散系统噪声分配矩阵；Wk-1表示离散系统噪声矩阵；Hk表示离散系统量测转移矩阵；Vk表示量测噪声矩阵。

假定系统噪声Wk与量测噪声Vk均值分别为qk和rk，即：

E[Wk]=qk,Cov(Wj,Wk)=Qkδjk

(22)

E[Vk]=rk,Cov(Vj,Vk)=Rkδjk

(23)

从理论上分析，利用卡尔曼滤波进行组合导航解算时，其系统噪声与量测噪声被视为白噪声处理，得到的估计并不是最优估计。Sage-Husa自适应滤波算法摆脱了传统卡尔曼滤波对噪声统计特性视为白噪声的束缚，其实时估算噪声统计特性，以此获得状态参数的最优估计。

Sage-Husa自适应滤波算法为：

(24)

(25)

(26)

(27)

(28)

Pk=(I-KkHk)Pk,k-1

(29)

(30)

(31)

dk=(1-b)/(1-bk+1)

(32)

式中，b为遗忘因子，一般取值在(0.95,0.99)。

在Sage-Husa自适应滤波算法中，虽能解决传统卡尔曼滤波由于将系统噪声与量测噪声视为白噪声而造成的滤波不稳定问题，但依旧存在2点缺陷：1)实时估算时，每次运算都需要对噪声的统计特性进行重复估计。迭代次数越多，滤波计算量越大，处理器负担越重，信息输出的实时性越差；2)不能同时动态估算量测噪声协方差矩阵Rk与系统噪声协方差矩阵Qk。

针对上述问题，引入滤波异常判定条件来减少非必要的估计次数。另外，上述基于新息序列vk的自适应滤波算法，主要解决外部量测噪声强度发生不确定变化的问题[9]，所以本文将在系统噪声协方差矩阵Qk已知的情况下估测量测噪声方差矩阵Rk。

1.4.1 调节因子γ的改进

引入滤波异常判定条件[10]：

(33)

(34)

式中，γ为调节因子，该值反映了判定滤波异常的严格程度。vk为新息序列，tr表示矩阵的迹。一般情况下，γ=1时滤波异常判别严格程度达到最大，此时可获取最优遗忘因子取值。

如果在滤波过程中，各参量迭代满足式(33)，则认定为滤波异常，说明先前的模型已不适用于当前的滤波。通过更新校正量测噪声协方差阵Rk，使其适应模型变化对滤波产生的影响，以提高系统的自适应性，增强滤波效果。

速度信息反映无人机在不同阶段内的飞行动态，因此，可以利用GPS输出的速度信息改进调节因子γ。在无人机飞行状态下，速度越大，飞行阻力越大[11]，与低速飞行相比，高速飞行无人机参数时变性更高[12]，更容易受工作环境和模式的影响[13]，也就更需要可靠的导航信息满足其飞行需求。因此，可以根据无人机飞行速度的大小来决定调节因子的取值。速度越大，调节因子取值越小，异常判据条件越严格。

改进的调节因子表示为：

γ=1+exp(-(a1vh+b1))

(35)

式中，vh为飞行速度，a1,b1为辅助调节因子，a1>0，两者取值可根据实际滤波异常判别严格程度设定。需要注意的是，调节因子的取值不能过大，否则滤波异常判别严格程度过小，引入滤波异常判定条件(式33)就无意义。上述改进过程选取指数函数形式，使得调节因子变化比较平缓，避免了由于速度急剧变化导致的调节因子大范围波动造成的滤波异常判别严格程度不足或者过严的问题。

1.4.2 最佳遗忘因子b的选取

为获取最佳遗忘因子b的取值，选取最严格滤波异常判定条件(γ=1)。根据式(33)和(34)可得以下关系：

(36)

满足式(36)则证明滤波异常，将新息序列vk、一步预测协方差阵Pk,k-1、量测协方差阵Rk代入式(33),可获得最佳遗忘因子取值[14]。

(37)

改进的Sage-Husa算法流程如图2所示。

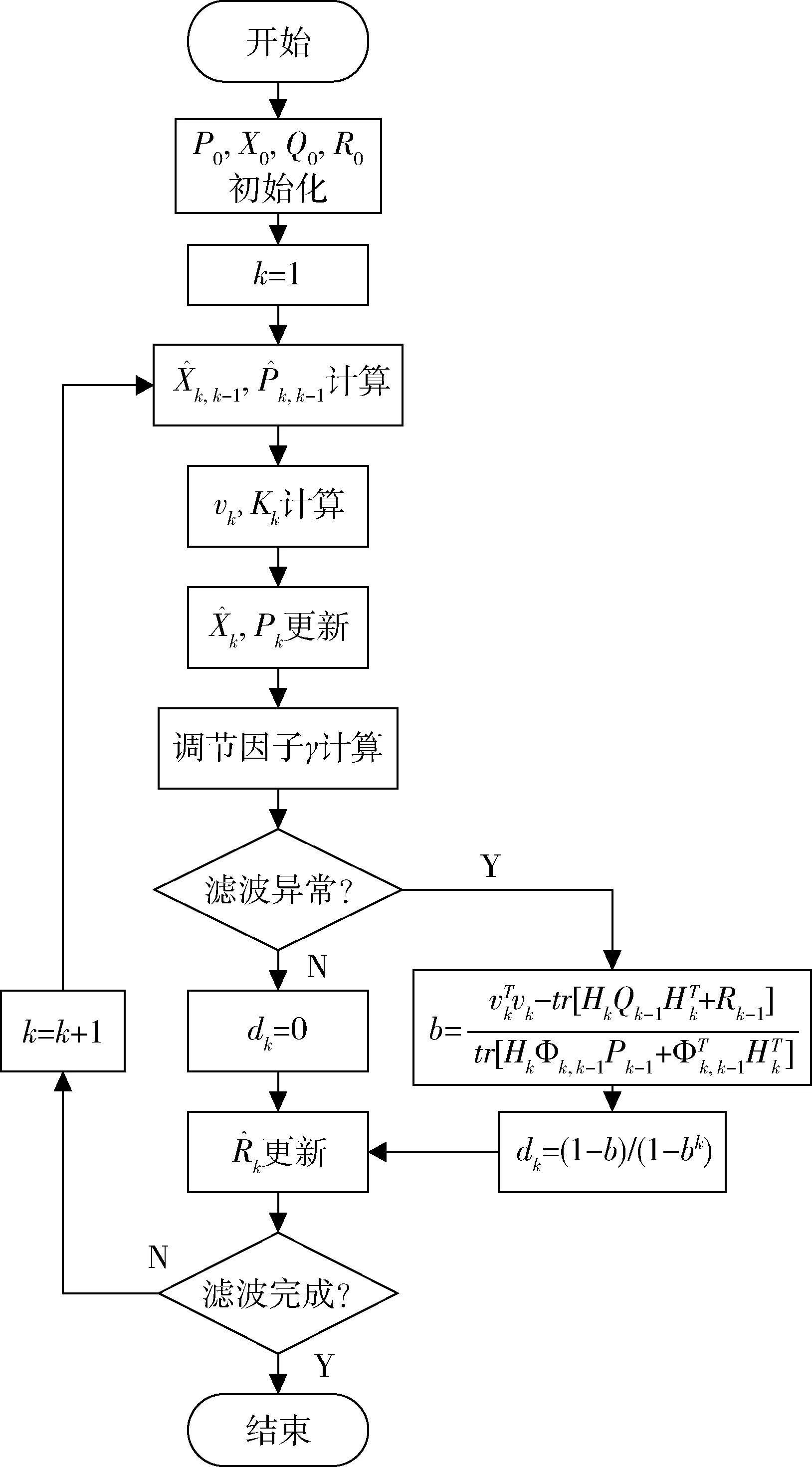
图2 改进调节因子的滤波算法流程

2 算法仿真及结果分析

为分析上述方法的可行性与正确性，利用模拟飞行数据进行了仿真实验。主要包括无人机三维航迹仿真模块、改进调节因子仿真以及导航传感器数据融合仿真模块。其中，三维航迹仿真模块模拟无人机实际飞行的理想位置和速度；改进调节因子仿真部分根据无人机动态数据改进调节因子，实时判定滤波是否异常；数据融合模块输出滤波校正后的位置信息。三维航迹仿真主要包括：短时间滑跑、加速爬升、定高飞行、转弯、减速飞行和俯冲等阶段。无人机飞行航迹如图3所示。

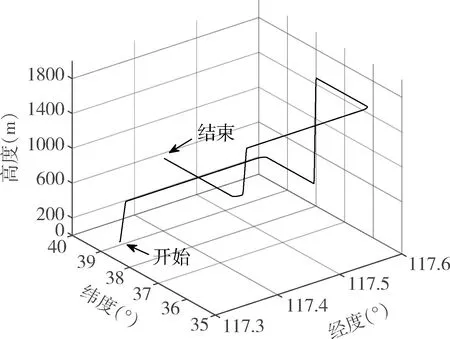
图3 无人机飞行航迹图

2.1 仿真条件设置

仿真以东北天坐标系作为导航坐标系， 起始位置设置为(39.10167° 117.34531° 100m)，仿真时间1000s，周期1s,传感器参数设置见表1。

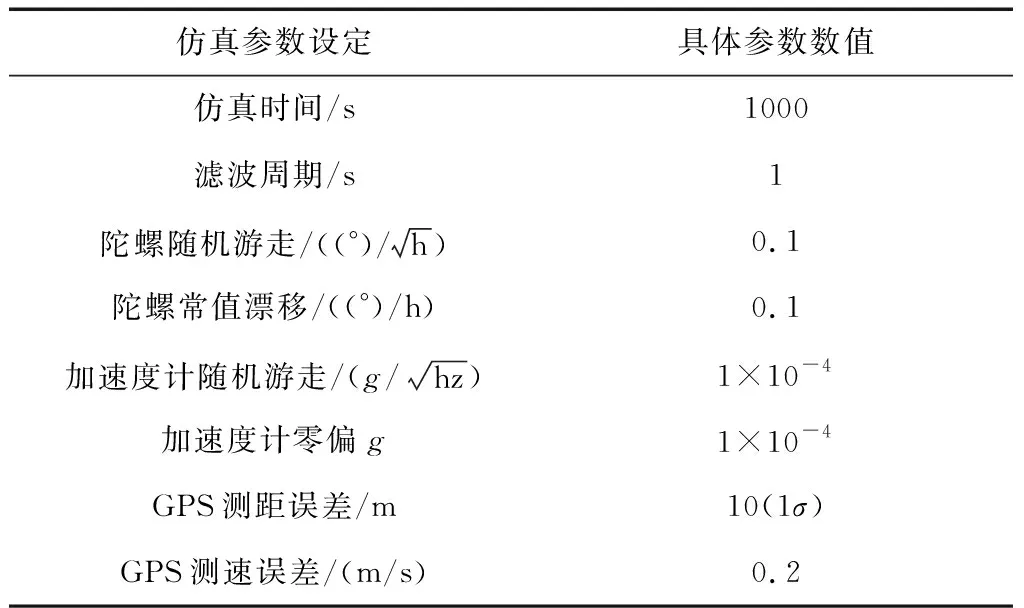
表1 仿真参数设置

2.2 仿真结果分析

通过仿真对比不同调节因子取值结果，确定改进方法的效果。同时采用传统卡尔曼滤波与改进的Sage-Husa自适应滤波分别进行信息融合，进一步验证改进算法的可行性。改进后的调节因子γ如图4所示。

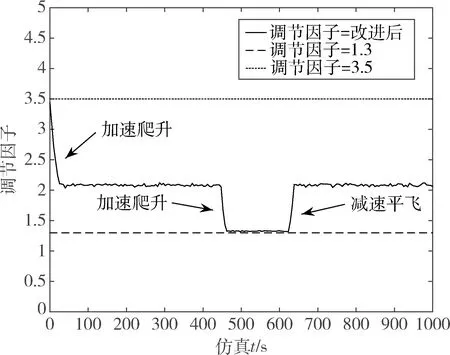
图4 调节因子变化曲线

由图4可知，改进后的调节因子的取值范围是1.3<γ<3.5，分别选择γ=1.3，γ=3.5作为固定调节因子参考值并进行对比实验。可见速度越大，调节因子取值越小，滤波异常判定程度越严格。

仿真模块对基于速度信息改进调节因子方法的滤波结果与固定调节因子(γ=3.5和γ=1.3)的滤波结果进行了对比，分别如图5～6中所示。

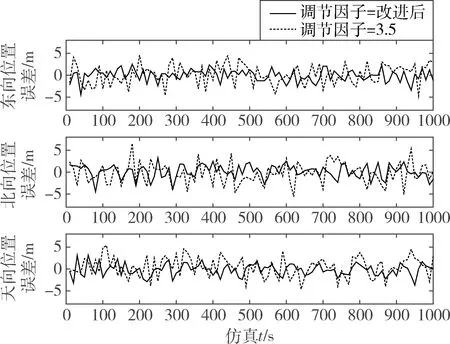
图5 γ=3.5及改进调节因子算法位置误差曲线

与未引入滤波异常判定条件相比，改进后的滤波算法仿真迭代次数减少了164次，有效减少了计算量。从图5中看出，调节因子γ=3.5时，固定调节因子算法滤波效果相较于灵活改进调节因子的滤波效果整体偏差。从图6看出，调节因子γ=1.3时，两者滤波效果整体上相当，但随着无人机速度的变化，固定调节因子算法出现了滤波不稳定现象，误差值甚至超过了相同时间段γ=3.5时的误差值。该现象主要集中在1s～40s，440s～480s和620s～640s的飞行时间内，此时飞行状态包括无人机两次加速爬升和一次定高减速飞行。以上结果可以看出，随无人机的飞行动态改变调节因子的取值可以有效确保滤波精度，并能在满足导航性能要求的前提下降低滤波计算量。图7与表2表示均方根误差情况。

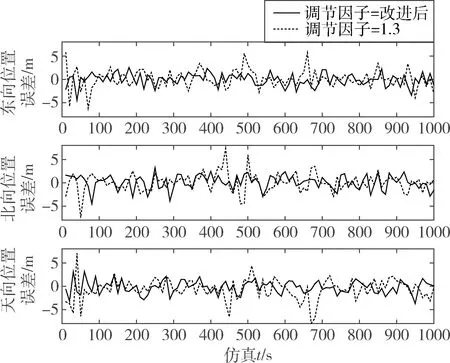
图6 γ=1.3及改进调节因子算法位置误差曲线

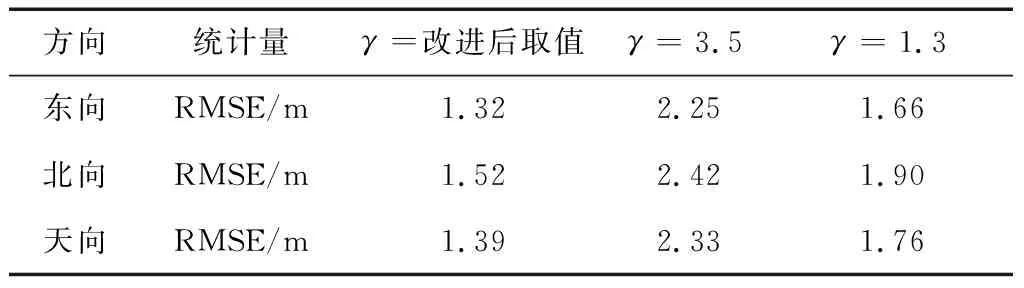
表2 各方向均方根误差值

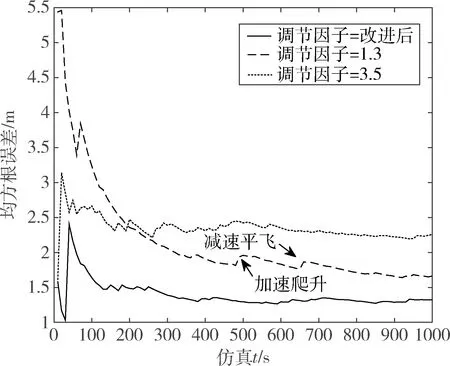
图7 东方向均方根误差曲线

由图7可知，改进调节因子的整体效果优于取定值时的仿真结果。调节因子γ=3.5时，其均方根误差相较于改进后调节因子，整体偏大。调节因子γ=1.3时，滤波严格程度提高，但无人机出现加速或减速等飞行速度变化时，均方根误差增大，在以上时间段内的滤波效果并不理想，而通过动态选取调节因子，达到的滤波效果较好。

为进一步证明改进后的Sage-Husa自适应滤波算法的正确性，分别采用2种数据融合算法进行仿真实验。

从图8可以看出，传统卡尔曼滤波具有一定的稳定性，但改进调节因子的滤波算法误差则趋近在一个更小的范围内。以东方向为例，分别采用2种数据融合算法时，均方根误差分别为2.85和1.32。仿真结果表明，虽然传统卡尔曼滤波能有效克服SINS误差累积的问题，但改进后调节因子的滤波算法滤波自适应能力更强，定位效果更好。

图8 位置误差对比曲线

3 结论

针对无人机高动态复杂情况下的导航需求，提出了改进调节因子的Sage-Husa自适应滤波算法。利用GPS速度信息约束改进算法调节因子，实时估计修正量测噪声协方差阵，以此调节状态增益，使之更好地适应当前滤波。仿真结果表明，相较于传统数据融合算法，改进的滤波算法可获得更稳定的定位结果，解决了传统卡尔曼滤波不能准确测量噪声统计特性导致滤波不稳定的问题，降低了自适应滤波算法的计算负荷，为高动态环境下的无人机组合导航提供了较好的解决方案。