平行双目视觉测量原理及实验研究

孙雷

（宿迁学院 江苏省宿迁市 223800）

随着机器觉技术的不断发展和进步，其在社会生活的各个领域发挥越来越重要作用。通过视觉的检测和识别功能，让许多流水线上具有高度重复性的检测工作都通过机器来完成，大大提高了生产效率、精度和自动化程度。常用机器视觉来代替人眼视觉，实现在一些危险工作环境下或者人眼视觉难以满足要求的场合下工作。除了工业上的应用，机器视觉技术在智能车方面也有广泛的应用。如美国密歇根大学的MOSFET系统智能车系统，意大利Parma大学ARGO智能系统；国防科技大学的CITAVT-IV等。智能车辆在行驶时需要实时地去感知自身和周围环境变化，包括检测车辆运行位置、姿态和车辆周围环境等等。目前市面上的测量方法有超声波测距、单目摄像头测距、双目摄像头测距这三大类。虽然超声波测距是最为简单一种，但测量范围非常有限，且所受环境影响程度较大，所以一般选择单目或双目测距法。单目测距虽然简单却误差较大，双目测距虽然复杂却精度较高。本课题主要研究如何获取场景中物体的深度信息，并且确保测量结果准确。因此本文主要研究双目视觉的测量原理、相机的标定、空间点的获取及空间距离的测量。

1 测量原理及模型

根据人眼仿生学原理可知，目标物体在人的左右眼所成呈现的结果是具有视差效果的，然后大脑经过加权处理等转化得到物体信息。双目视差测距通过平行放置的两台摄像机代替人的眼睛，从左右两个角度对被测物体采集图片；利用计算机代替人脑对所拍摄的图片进行处理。然后将获取到图片结合三角测量原理计算出物体距离，即可获取空间物体三维坐标信息或者深度值。

图1为双目视差测距示意图。P（Xw,Yw,Zw）为空间中的一个特征点，点P在双目摄像机成像平面投影点分别为P和P。如何根据被测物体的特征点P的投影坐标来求解被测物体特征点P的Zw的坐标值是测量需要解决的问题。

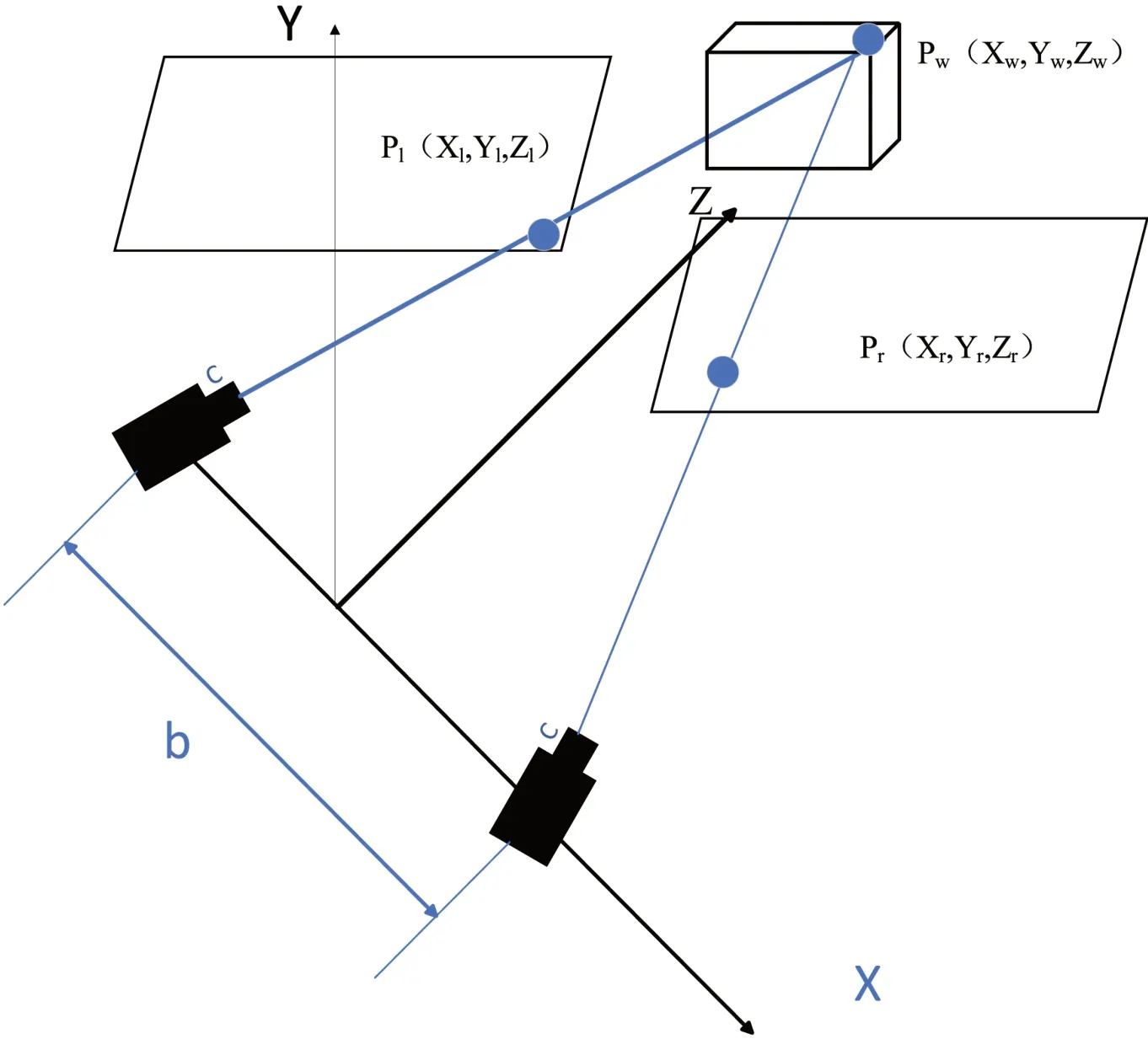
图1：双目视觉测量示意图

由于光是沿着直线传播，空间特征点P可视为两个相机的投影中心点与成像点连线的交点。该俯视图（有效焦距f，基线间距为b）中平行的两个面为成像平面，平面上y轴坐标必然相同，只是x轴的坐标值不同， P 在左相机的投影点坐标为 XL，右相机的投影点坐标为XR，如图2所示。

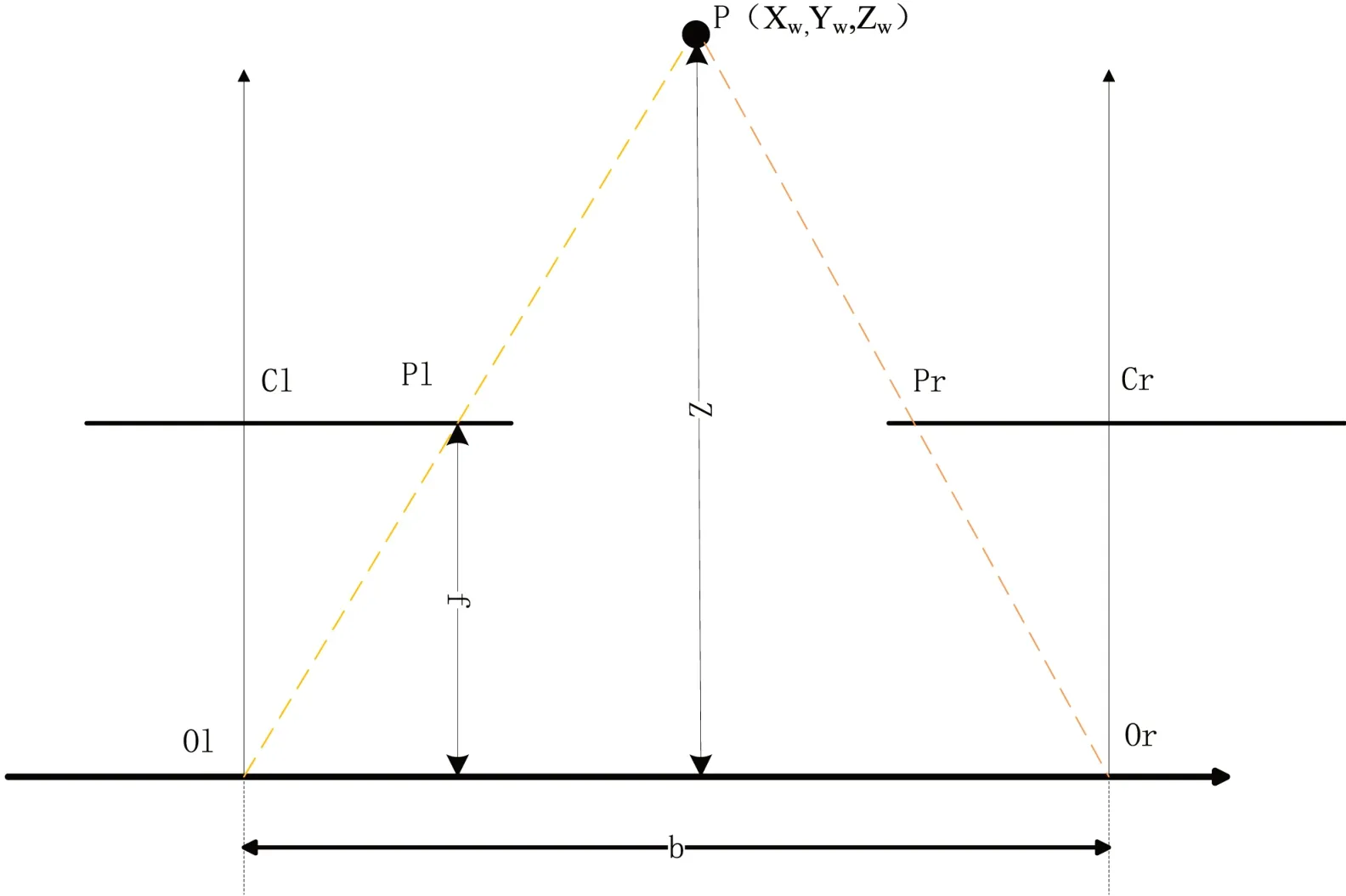
图2：双目视差几何模型

线段x和x分别是左相机投影点到左成像面的距离、右相机投影点到右成像面的距离，则点 P的摄像机视差值按定义如下：

即两个成像点P和P之间的距离（视差）为：

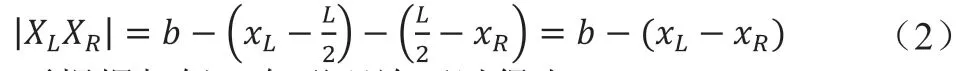
再根据相似三角形理论可以得出：

则可以得到点P到投影中心平面的距离z：

式中：f为摄像机焦距

b为基线距

d为P的视差值

2 摄像机标定

摄像机标定过程就是确定摄像机的几何和光学参数。经典的小孔成像模型是一种理想条件下的线性成像模型。但实际由于镜头的畸变的存在，无法准确表述拍摄图像中的几何关系。摄像机非线性模型考虑了图像畸变的影响，将图像畸产生的像素误差降到最小。

镜头畸变根据畸变方向主要分为径向畸变和切向畸变。径向畸变定义为沿着透镜的半径方向，产生图像的畸变。其产生的原因是主要光线远离透镜中心的地方相比透镜中心的地方更加弯曲。因此畸变的数学模型可以用图像中心的泰勒级数展开式的前几项进行描述，径向畸变的计算公式为：

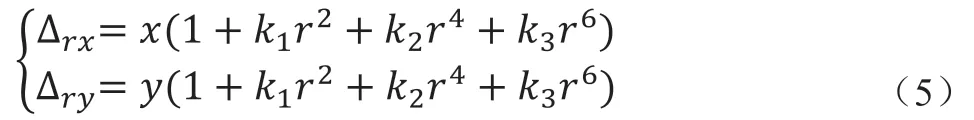
式中：k、k、k为径向畸变系数，通常使用前两项，即k1和k2即可。如果摄像机镜头为鱼眼镜头需要考虑k3带来的影响；（∆，∆）为坐标点在成像平面上的原始位置；（x，y）是坐标点受到畸变后新的位置。切向畸变是由于透镜本身与摄像机传感器平面或与图像成像平面不平行而导致的。计算公式为：

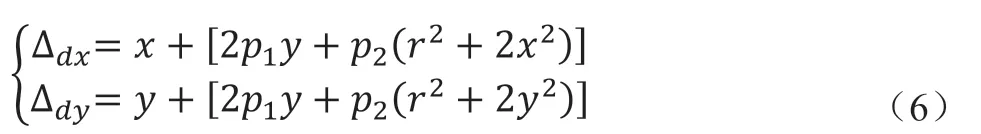
式中：p1、p2为畸变模型参数

传统标定法的标定板是三维立体。虽然精度非常高，实现起来却比较困难。而张正友教授提出的方法介于传统标定法和自标定法之间，克服了传统标定法需要高精度标定物的缺点。张正友相机标定法是张正友教授1998年提出的单平面棋盘格的相机标定方法。标定过程仅需使用一个黑白棋盘格就可以。该方法与自标定相比，提高了精度且便于操作，被广泛应用于摄像机参数标定实验。

3 角点检测

克里斯•哈里斯和迈克•斯蒂芬斯在他们的论文《一种结合了角和边缘的探测器》中试图找到一些特殊的点，并把这个简单的想法转化为数学表达。其检测算法数学思想为：使用一个固定窗口在图像上进行任意方向上的滑动，比较滑动前与滑动后两种情况下，窗口中的像素灰度变化程度。如果存在任意方向上的滑动，都有着较大灰度变化，那么我们可以认为该窗口中存在角点。

根据该算法思路去检测图像像素的灰度变化情况，即求解：

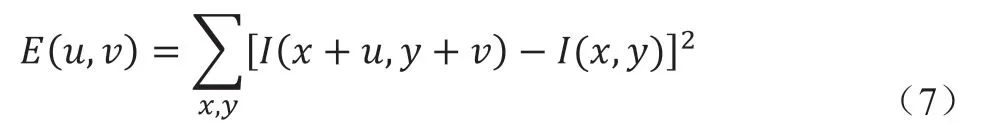
式中：I(x+u,y+v)表示像素（x，y）周围像素的亮度值。I(x,y)表示像素（x，y）的亮度值。对于上式，我们希望找到使E的值尽量大的点，则将上式右边I(x+u,y+v)泰勒展开并省略高次项可得：

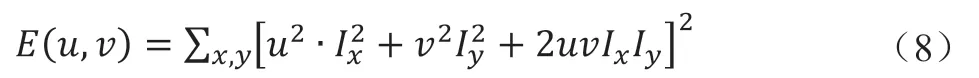
最终将式子转化为：

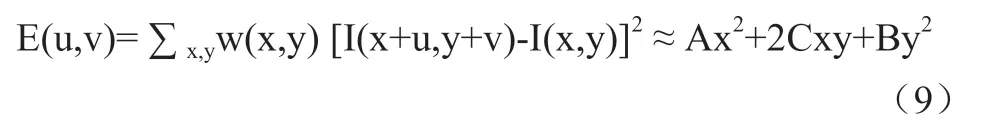
其中w是以（x,y）为中心点窗函数， M为得到海森矩阵：

虽然根据二次函数特征值的计算方法可以求得特征值。但Harris的角点计算方法并不需要计算具体的特征值，而是计算一个角点响应值R来判断角点。角点响应函数R为：

其中，det(M)=λ×λ为矩阵的迹，trace(M)=λ+λ为矩阵的迹，k为经验常数，k的值越小，能检测到的特征点越多。

4 双目视觉系统测量平台与实验结果分析

4.1 测量系统介绍

摄像机部分包括双目摄像头和支承部分。三角架保证了相机的平稳，利用自制的人工十字标定板实现角点提取效果，通过改变被测物平面与像机平面位置关系，验证不同距离的测量结果。图3为本实验选用双目像机，型号为HBV-1780-2 S2.0。技术参数为：基线距离60mm，100万像素，像元尺寸3μm×3μm，镜头尺寸1/4英寸。该像机系统自带驱动，通过usb数据线与window10电脑相连接，即可实现图片采集。

图3：双目系统

4.2 测量实验与分析

将双目摄像头连接到计算机上，利用双目摄像头对不同位姿与不同方向的棋盘格进行采集。利用MATLAB标定工具箱对摄像头进行标定。本实验总共采集40张照片，其中左相机为20张，右相机20张。表1为标定结果。

表1：双目摄像机参标定结果参数表

RotationOfCamera2是相机2相对于相机1的旋转矩阵，为相机像机外部参数旋转矩阵R。TranslationOfCamera2是相机2相对于1的平移矩阵，像机外部参数平移矩阵T。k1、k2、k3为径向畸变系数，P1、P2切向畸变系数。u0、v0 为图像主点。焦距fx、fy分别为左右摄像机的焦距，并且可以通过像元大小计算出有效焦距f。

为了测出空间靶标的距离，按照顺时针方向对十字靶四个点标号。对原始图片进行校正后，并运用harris角点方法提取得到十字中心的四个点坐标。下图为校正后图片角点的提取结果。对这四个角点做平均获得最终的视差值。

深度信息z的计算需要基线距b、相机焦距f和视差值d三个参数。其中双目摄像机基线b为60mm，视差值d可通过图像特征点提取到的像素坐标获取，像机焦距f可以由标定实验获取。为验证测距效果，本研究对靶标在50mm-250mm不同距离进行测量实验，测量结果如表2所示。图4是深度为75mm时候角点提取的图片及视差计算表格。表3为不同距离时误差计算结果。

图4：左右相机校正后角点特征

表2：深度距离为7.5cm

表3：距离测量结果

通过以上实验结果可知，随着测量距离的增大误差增大。引起误差的主要因素是摄像机的标定精度及未考虑双目校正问题。在标定过程中，由于标定参数计算是通过标定图的一些物理参数来获取各项未知量的系数，进而通过牛顿-迭代法进行方程的求解，所以标定图的精度会直接影响到图像处理算法的效果。作为初步实验,本文的标定图为手工绘制打印，标定板存在一定的误差。其次在对标定板进行双目摄像机标定时，要将标定板放在摄像机的视场角范围之内，并调节好镜头的焦距和光圈，能够获得成像清晰的标定图；拍摄时手持标定板应处于静止状态或是小幅度的晃动，以减少由于相机的曝光时间引起的运动模糊。还有为了获取不同迭代条件，应该让标定板尽可能在视场角内不同位置进行拍摄，在深度方向上给予一定的位移或者将标定板旋转一定角度。最后双目相机光轴并非完全平行，导致在垂直方向上存在一定误差，计算视差时会引入一定的误差，下一步将进行双目校正，使其光轴平行左右平面共面，消除垂直方向上的误差值。

5 结论

本文通过仿生学原理的分析得到了双目视差的几何模型，推导了深度信息的计算公式。然后讨论了图像畸变的产生原因及校正方法。运用了角点检测方法提取待测特征点。最后通过分组测距实验验证测量方案的正确性，并且给出了下一步降低误差的方法。双目视觉测距理论及方法可以运用到智能车上实现障碍物距离测量。