基于GA-BP神经网络算法的绞线串扰预测

杨铮

（江苏省医疗器械检验所 江苏省南京市 210019）

1 引言

绞线是一种结构特殊的非均匀传输线，因其较强的抗干扰能力而广泛应用于高频率、高损耗场景。绞线也因其拥有良好的机械性、柔韧性而适用于航天航空、汽车等特殊领域的信号传输。文献最早对双绞线串扰进行了相应的研究，随后大量的学者开始研究场线耦合下绞线的抗电磁干扰。但是由于绞线寄生参数的不确定性，其内部串扰缺乏研究。

非均匀传输线串扰研究方法同样适用于绞线，唯一的区别在于绞线寄生参数提取缺乏有效的方法。基于级联思想，非均匀传输线可以等效为有限微元小段的级联，单个微元小段可以近似为均匀传输线，其传输线方程可由其RLCG寄生参数矩阵表征。现有的文献大都利用计算电磁数值方法来提取非均匀传输线的寄生参数。文献对传输线系统进行分析时引入FDTD算法，进而获取了传输线时域差分模型，最后从场解中提取了寄生参数矩阵。在中，利用有限元法（FEM）解决电磁参数的提取问题，提取基于等效介电常数处理介质分层面问题。

数值法既有精度缺陷又有适用条件限制，现代人工智能算法却可以较好的处理计算效率和计算精度共存的问题。文献正是基于这一思想，引入BP神经网络来构建绞线电磁参数矩阵随绞线轴向延伸间的非线性映射关系，最终结合时域有限差分算法（FDTD）完成绞线串扰预测。BP神经网络依赖于初始网络权阈值，对于不同权阈值初始化后网络往往会得到不同精度的解。遗传算法能够解决BP神经网络陷入局部最优问题，其优化BP神经网络的权值和阀值，解决BP神经网络对于初始权值的敏感性问题。相较于常规的BP神经网络，经GA优化后的BP神经网络展现了更高的精度。最后在绞线串扰的求解分析部分，为了FDTD算法计算复杂、占用计算机内存大的问题，本文将绞线寄生参数矩阵提取模型与模量解耦法结合对一实例三芯绞线的近端串扰、远端串扰展开预测研究。

本文的结构如下：在第二部分中建立多导体传输线串扰模型并利用模量解耦法求解传输线方程。第三部分中论述了基于GA-BP神经网络算法提取绞线寄生参数的具体实现流程。第四部分中利用本文提出的GA-BP算法结合模量解耦法研究一实例三芯绞线模型并进行了串扰的仿真验证和分析。在第五部分中给出了本文的结论。

2 多导体传输线模型分析

基于级联的思想，分析多导体传输线时可以对其作微元化处理，即多导体传输线由有限个Δz长度的微元小段构成，在小段内多导体传输线可以等效为等值电路形式，便于进一步分析其串扰效应，如图1所示。传输线的耦合效应可完全利用该模型表征，具有较高精度。其中，l、l表示传输线单位长度的自感，l代表传输线之间的单位长度的互感；r、r分别表示传输线单位长度的电阻；c表示传输线之间单位长度的互耦电容，c、c表示传输线分别对地的耦合电容；g和g表示传输线之间单位长度的漏电导。

图1：单位长度多导体传输线等效等值电路

根据多导体传输线理论可以得频域多导体传输线方程：

其中Z为单位长度阻抗矩阵，Y为单位其长度导纳矩阵，可由RLCG寄生参数表示为：

本文采用模量解耦法求解上述传输线方程，得到传输线终端响应，即串扰值。由此可见，对于多导体传输线，只需得到阻抗矩阵Z和导纳矩阵Y，即可实际解出平行线缆串扰。

3 GA-BP神经网络算法提取绞线RLCG寄生参数

3.1 绞线结构分析

从传输线轴向角度出发，绞线可以看作由无数个连续旋转着的横截面的组合。图2说明了单个节距内三芯绞线横截面的连续旋转和线的轴向延伸过程。从图中可以看出三芯绞线初始横截面旋转2π/3角度后得到与初始横截面形状一致的横截面，仅存在传输线人为定义序号的差异。

图2：三芯绞线单节距变换模型

随着绞线的轴向延伸绞线的横截面形状也在发生改变，与之对应的是绞线寄生参数的变化，即绞线轴向坐标与绞线寄生参数间存在一种非线性映射关系。利用函数关系可以表示为：

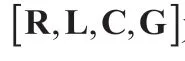
通过对绞线的结构分析以及换位处轴向长度与其对应旋转角度的关系，可以将绞线上任一点的坐标转换为绞线在该点处的旋转角度，以公式表示为：

式中，l是绞线轴向坐标，θ是旋转角度，p是节距，d是绞线总长。

由公式（3）可将公式（12）转换为：

3.2 GA-BP神经网络

公式（5）可知该非线性映射为单输入（角度或绞线位置），输出为RLCG寄生参数，选取一单隐藏层可以确定BP神经网络的拓扑如图3所示。本文以横截面旋转角度作为神经网络输入，以RLCG寄生参数作为BP神经网络输出。

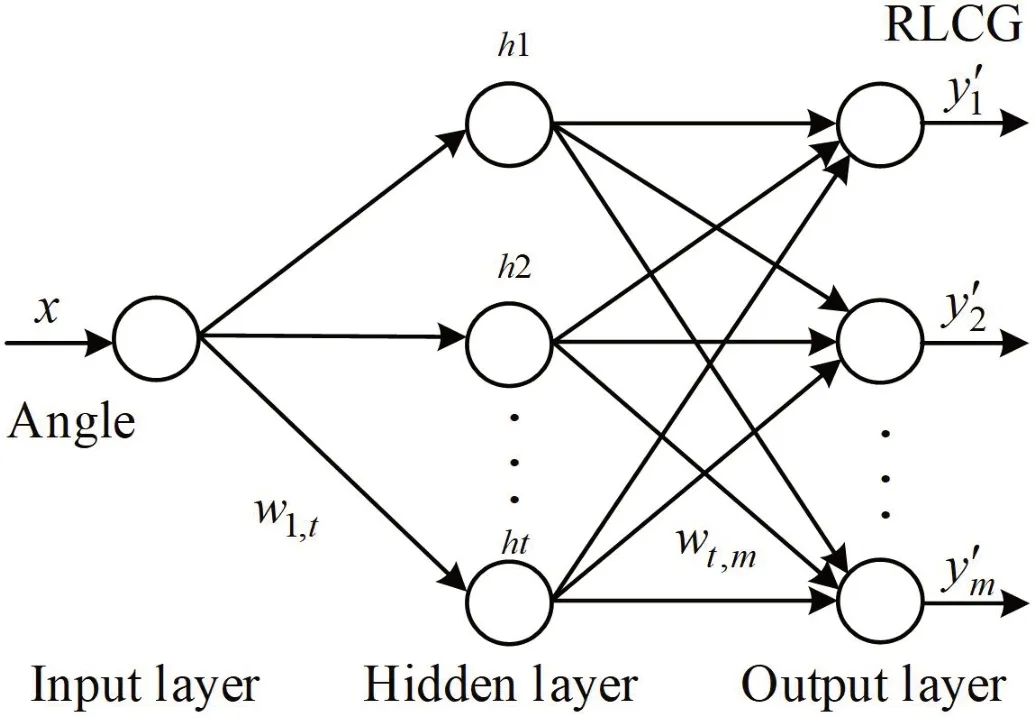
图3：BP神经网络拓扑结构

BP神经网络的应用效果受其权值和阈值初始值的影响很大，因此神经网络正向传播时，容易陷入局部极小值，影响预测效果。本研究采用遗传（GA）算法对BP神经网络的权值和阈值进行优化，形成新的GA-BP神经网络算法，并将其应用于绞线RLCG寄生参数分析计算。

GA优化BP的步骤如下：

（1）训练样本归一化。使用最大最小值归一化对训练样本进行数据压缩，保留数据特性的同时，加快训练速度。

（2）初始化BP神经网络算法。确定BP神经网络拓扑结构，根据训练样本确定隐藏层单元数、学习速率与激活函数等网络参数，生成相应的网络拓扑结构。

（3）初始化遗传算法。生成初始种群，随机生成权值与阈值的初始值，并将其作为种群的个体，进行实数编码。定义染色体编码长度l，则对于1-M-N拓扑的BP神经网络有：

（4）确定适应度函数。以测试数据的均方根误差 MSE作为适应度评价函数，用于评价染色体，表现为：

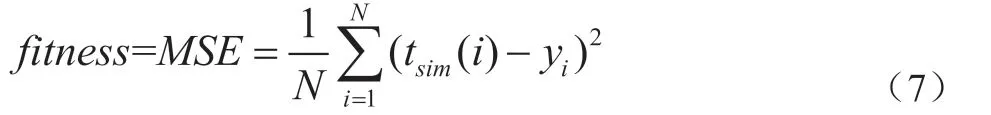
式中：N为训练集样本数；t(i)为第i个样本的预测值；y为第i个样本的实际值。因此，算法迭代停止时适应度函数值最小即为最优解。

（5）选择父代。按适应度大小对个体进行排序，并使用赌轮盘算法筛选出2个个体作为父代。计算个体最优适应度bestfintness，记录最优个体染色体编码bestchorm。

（6）随机交叉。父代以每层网络的权值与阈值作为基因，采用随机交叉算法，以一定的交叉概率p对基因进行组合生成新的子代。

（7）变异操作。生成子代中，有一定的概率p存在一部分个体发生变异，变异个体的权值和阈值将重新赋值，生成新的基因。

（8）迭代更新求解最优个体。如果下一代最优个体适应度优于上一代，则更新bestfintness、bestchorm；反之保持不变，淘汰最差个体。

（9）迭代停止条件。在不满足停止条件时，从原始种群中选择部分适应度高的个体与新生成子代组成新的种群，重复（5）～（8）的步骤继续求解满足情况的权值与阈值。

4 验证与分析

为方便研究，本文以三芯绞线为例对本文所提方法进行验证与分析。线束参数如表1所示。对地的具体分布图形如图4所示。

表1：三芯绞线参数

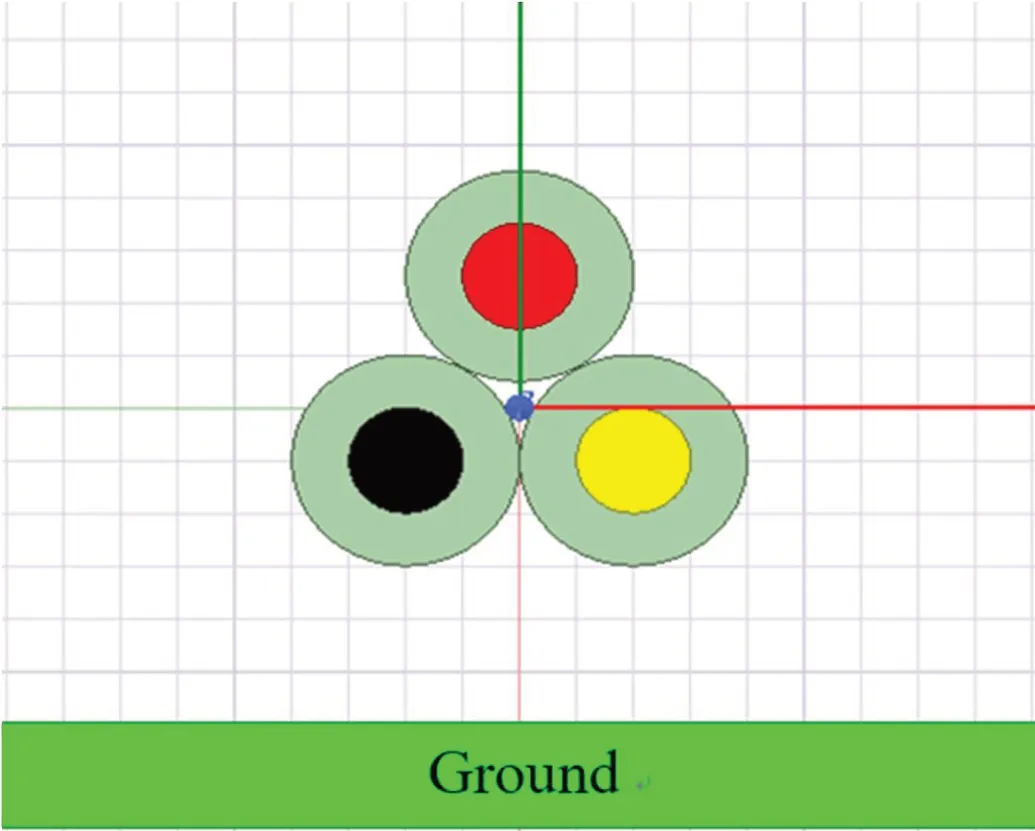
图4：三芯绞线模型参考截面图

以图4中旋转度数为0°的线束截面作为参考截面，利用Ansys Q3D仿真软件对其单个节距内RLCG参数矩阵进行提取，得到参数预测所需的样本。并以任一线作为激励线，定义为1号线，则2、3号线为受扰线。利用基于GA-BP、BP神经网络算法的绞线RLCG参数矩阵提取方法和模量解耦算法联合对绞线2、3号线上串扰进行预测。以全波仿真算法传输线矩阵法TLM求解的串扰结果作为参考标准。在0.1MHz-1GHz内利用三种方法求解的近端串扰结果如图5、图6所示。三种方法求解的远端串扰结果如图7、图8所示。

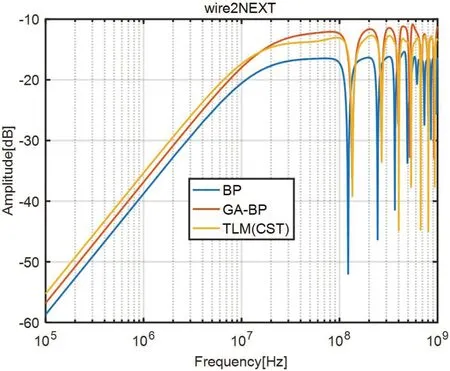
图5：2号导体NEXT

图6：3号导体NEXT

图7：2号导体FEXT

图8：3号导体FEXT

由于三芯绞线结构的对称性，在初始频率0.1MHz处，2、3号线上TLM算法的近端串扰表现为-55.27dB。GA-BP算法表现为-56.81dB，与参考标准相差1.54dB；BP算法表现为-58.68dB，与参考标准相差3.41dB。此后，GA-BP算法与TLM算法趋于一致，稳定增长后于高频处在-15dB上下波动。而BP算法虽然也在稳定增长，但始终与前两者保持较大的数值差异，且在100MHz后呈现频率偏移差异。在关键频率处分析三种方法求解的绞线串扰，结果如表2、表3所示。

表2：2号线近端串扰的算法与仿真对比(dB)

表3：2号线远端串扰的算法与仿真对比(dB)

通过对串扰结果的分析可知，GA-BP算法求解的NEXT和FEXT与参考标准具有较高的吻合度，而BP算法则与前两者存在较大的数值差异和频点偏移。这说明了经GA算法优化后的BP神经网络具有更好处理绞线串扰预测问题的能力，验证了本文所提基于GA-BP算法结合模量解耦法预测绞线串扰方法的高精度和高效率。

5 结论

本文提出了一种基于GA-BP算法的绞线RLCG参数矩阵提取方法。实际上，任何满足一定数学关系的空间布线都能够通过本方法提取高精度的RLCG参数矩阵。文中通过建立多导体传输线串扰模型，利用模量解耦法求解传输线方程。之后，通过对绞线的建模分析，引入GA-BP神经网络提取绞线寄生参数。最后，将绞线寄生参数矩阵结合模量解耦法预测绞线串扰，并通过数值实验验证了本文方法预测绞线串扰的有效性和适用性。在工程应用中，NEXT和FEXT预测的结果可以直接为线路的布局、选型、调参提供理论参考意义。