基于多尺度量子熵的中介轴承故障诊断方法
2022-09-09田晶张羽薇张凤玲艾辛平高崇
田晶,张羽薇,张凤玲,艾辛平,高崇
沈阳航空航天大学 辽宁省航空推进系统先进测试技术重点实验室,沈阳 110136
中介轴承是航空发动机双转子支承系统的重要组成构件之一,现代航空发动机多采用双转子结构的形式使得中介轴承承受着巨大的工作压力。由于中介轴承介于两个高低压转子之间,难以润滑,并且轴承的工作环境极其恶劣,极易发生故障。因此,掌握中介轴承的状态监测及故障诊断技术是至关重要的。
在中介轴承故障诊断研究中,故障特征提取的可靠性会直接影响诊断结果是否准确可靠,因此对故障信号进行特征提取是中介轴承故障诊断研究中的重要环节。随着非线性动力学理论的发展,近似熵、样本熵、多尺度熵、排列熵(Permutation Entropy, PE)、模糊熵(Fuzzy Entropy, PE)、层次熵等非线性动力学参数得到广泛应用。Richman和Moorman提出了样本熵的概念,相较于近似熵,样本熵鲁棒性更强,赵志宏等对轴承振动信号的样本熵深入分析,结果验证样本熵的有效性。针对样本熵算法中存在的缺陷, Costa等引入一种基于多尺度熵(Multiscale Entropy, MSE)的故障特征提取方法,郑近德等将多尺度熵作为诊断转子系统故障的特征参数,该方法能够有效地进行故障类型诊断,但是在粗粒化过程中存在信息丢失的缺陷,且计算较耗时。排列熵是由Bandt和Pompe提出的一种时间序列复杂度和随机性描述的动力学参数,具有所需时间序列短,对信号突变敏感,计算速度快,适用于非线性信号等优点。Yan和Gao将排列熵作为检测旋转机械工作状态的评判依据,结果表明,排列熵能够有效地提取出微弱信号的故障信息。在PE方法的基础上,Aziz和Arif提出了多尺度排列熵(Multiscale Permutation Entropy, MPE),用于估计不同尺度下时间序列的复杂度,但是MPE抗噪声能力较弱,无法捕捉到信号内在微小动力学变化。近年来,随着量子理论不断被完善,人们对于量子理论的关注也渐渐提高。受量子信息处理技术的启发,谢可夫和罗安提出了叠加态结构元素和基于叠加态结构元素的数学形态学运算,拓展了传统形态学运算的意义。叠加态结构元素的引入,使得对结构元素的描述更为灵活,结合量子力学的叠加原理与信息熵理论,提出一种基于多尺度量子熵(Multiscale Quantum Entropy, MQE)的特征提取方法。
由于中介轴承故障源到传感器安装位置的传递路径较长,实验信号的故障信息将被系统噪声所削弱,使早期故障诊断十分困难。空域相关是基于小波变换的一种降噪方法,该方法在信息处理、电子通讯、图像处理等领域均取得了突出成就。Witkim在信号处理时首次采用了尺度空间相关原理,Xu等进而提出了空域相关降噪(Spatial Correlation Decline,SCD)方法,用于信号降噪处理过程中。苏哲等采用小波阈值和空域相关滤波算法对脉冲星信号进行了消噪处理,实验结果表明该方法能在抑制噪声的同时保留信号微脉冲等边缘细节。空域相关降噪方法可以保留更多振动信号的细节信息,提高信号的信噪比,进而提高故障诊断准确率。本文将空域相关去噪方法引入到中介轴承的振动信号预处理中。
为了提高故障诊断的准确性,在采用MQE提取降噪后的中介轴承振动信号的故障特征后,进行多点传感器故障信息融合处理。由于多点提取振动信号多尺度量子熵组成的故障特征样本数据量大,存在一定的信息冗余,会影响识别效果,因此,需要对提取的故障特征进行降维融合。局部线性嵌入(Locally Linear Embedding,LLE)算法采用局部邻域线性重构系数保持局部数据结构进而达到对非线性数据结构进行约简。该算法可以在降低计算量的同时,提升故障诊断准确率。Li等分析了现有图像分辨率方法的不足,并将LLE算法应用于估计分辨率大小,实验验证了LLE算法的优越性,因此,本文采用LLE算法对于多传感故障信号提取的MQE进行特征维数约简。最后鉴于概率神经网络(Probabilistic Neural Network, PNN)能用线性学习算法实现非线性分析,具备学习速度快、鲁棒性强、可以完成任意非线性逼近的优点,采用PNN对故障模式进行自动识别。
基于上述理论,提出了一种基于SCD、MQE、LLE与PNN相结合的故障诊断方法。为验证所提出故障诊断算法的有效性,搭建试验台开展中介轴承典型故障模拟实验,对中介轴承振动信号进行检测分析。结果表明,提出的方法不仅能够有效地实现中介轴承不同故障类型的准确诊断,而且识别率较高。
1 量子理论
1.1 量子理论的基础
量子比特是量子力学中的概念,基于叠加原理,量子比特可以理解成由2种不同量子态线性叠加所组成的1个双稳态系统,具体表示为
|〉=|0〉+|1〉
(1)
式中:系数和表示|0〉和|1〉出现的概率,并且和满足归一化条件:

(2)
1.2 振动信号多量子位系统
在中介轴承振动信号处理中,需要对振动信号的每个采样点进行量子化,每组个采样点的振动信号可由个量子位描述,其中第个量子位的状态为|()〉=|0〉+|1〉,该振动信号可用个量子比特的直积表示:
|〉 = |(1)〉⊗|(2)〉⊗ …⊗|()〉=
αα…α|00…0〉+αα…
αβ|00…01〉+ββ…β|11…1〉=

(3)
式中:|〉表示含个量子比特的量子系统(振动信号)|〉的第个态矢;为态矢|〉的概率幅值。
2 多尺度量子熵
2.1 量子熵算法
借鉴信息熵的优势,结合量子理论,提出了量子熵(Quantum Entropy, QE)的概念。其计算流程为
1) 时间序列归一化
考虑长度为的时间序列={(),=1, 2,…,},对其进行归一化,得到归一化后的时间序列为={(),=1, 2, …,}。
2) 相空间重构
重构矩阵计算结果为


(4)
式中:为嵌入维数;为延迟时间;()为重构分量。
3) 重构分量量子化
|()〉=,1|00…0〉+,2|00…〉+…+

(5)
式中:,为态矢|〉的概率幅值。
4) 量子熵计算

(6)
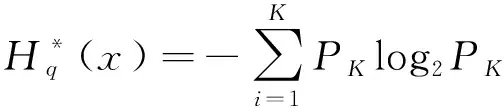
(7)
5) 量子熵标准化
对量子熵进行标准化处理,得

(8)
2.2 多尺度量子熵算法
鉴于多尺度分析能够克服单一尺度分析的不足,可以更加全面地对故障特征进行分析,在量子熵的计算方法上结合多尺度分析,提出多尺度量子熵的概念,其计算过程为
1) 对于长度为的时间序列={(), 1≤≤}, 构建粗粒化向量:
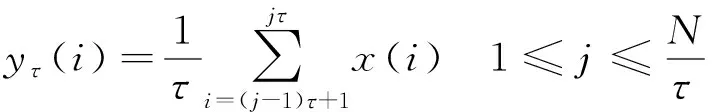
(9)
式中:为尺度因子。其粗粒化过程如图1所示。
2) 求取每一个粗粒向量的量子熵,并将得到的个粗粒向量量子熵的值表示成尺度因子的函数:
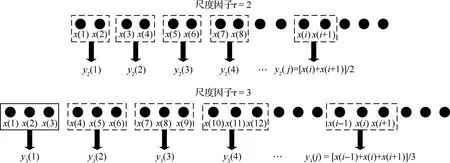
图1 粗粒化过程示意图Fig.1 Schematic diagram of coarse graining process

(10)
MQE值的大小表示时间序列的复杂度和随机程度。MQE值越大,时间序列复杂度越高,MQE值越小,时间序列复杂度越低,振动信号的规律性也越强。
2.3 多尺度量子熵算法参数选择
多尺度量子熵在计算过程中,嵌入维数、时间延迟和数据长度对计算结果均存在不同程度上的影响。以白噪声作为研究对象,分析上述参数对多尺度量子熵的影响。
1) 嵌入维数的影响
设数据长度为=4 096,时间延迟为=1,分别计算嵌入维数=2,3,4,5,6,7时的多尺度量子熵值,计算结果如图2所示。曲线的平稳度可以通过极差和标准差来判定,不同嵌入维数下多尺度量子熵的极差和标准差柱状图如图3所示。
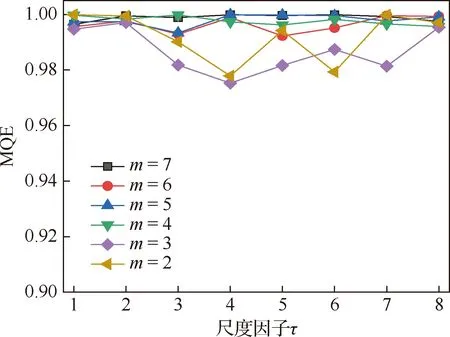
图2 不同嵌入维数下的多尺度量子熵Fig.2 MQE curves of different embedding dimensions

图3 不同嵌入维数下多尺度量子熵的极差和标准差Fig.3 Range and standard deviation of MQE under different embedding dimensions
嵌入维数的取值对多尺度量子熵值的计算结果存在较大的影响,取值较小时,重构的序列中存在信息丢失的现象,取值较大时,重构向量与原始信号的相似性降低,信息熵将无法表征原始振动信号的故障特征,且计算耗时量也较大。从图2和图3可以看出,当嵌入维数=2、=3时,多尺度量子熵值波动较大,不能有效地检测时间序列的动力学突变。当嵌入维数=6、=7时,多尺度量子熵值波动较小,但是计算量较大。当嵌入维数=4、=5时,多尺度量子熵值极差和标准差较小,曲线较为平稳,波动不明显,且计算时间也在合理范围内。=5时曲线平稳性高于=4时,综合考虑各种因素,取嵌入维数=5。
2) 数据长度的影响
设嵌入维数为=5,时间延迟为=1,数据长度分别设定为=512、4 096、8 192、32 786、65 536。 计算结果如图4所示。
从图4中可以看出多尺度量子熵值曲线随着数据长度的增加逐渐趋于平稳状态,波动程度也逐渐降低,不足之处是计算时间会随之增加。当=4 096时,多尺度量子熵值随尺度因子的增加基本保持不变,且计算时长在合理范围内。因此,取数据长度=4 096。
3) 时间延迟的影响
设数据长度为=4 096,嵌入维数为=5,时间延迟分别设定为=1、2、3、4、5、6。计算结果如图5所示。从图中可以看出各时间延迟下多尺度熵值差异性较小,考虑到计算时长的影响,取时间延迟=1。

图4 不同数据长度下的多尺度量子熵Fig.4 MQE curves of different data lengths

图5 不同时间延迟下的多尺度量子熵Fig.5 MQE curves of different time scales
2.4 仿真信号验证
鉴于高斯白噪声和粉红噪声作为自然界中常见的两种随机的时间序列,其信号均具有规律性,并且其信息熵存在标准值以及变化趋势,因此采用数据长度=4 096的高斯白噪声和粉红噪声信号验证多尺度量子熵的有效性及优越性,对这两种噪声信号进行傅里叶变换得到时域波形和频域波形如图6所示。

图6 白噪声和粉红噪声时频域波形图Fig.6 Time-frequency domain waveforms of white noise and pink noise
接着采用多尺度量子熵、多尺度排列熵和多尺度模糊熵(MFE)对两种噪声信号分别进行特征提取,提取结果如图7和图8所示。

图7 高斯白噪声下3种不同算法的熵值Fig.7 Entropy values of three different algorithms for white noise

图8 粉红噪声下3种不同算法的熵值Fig.8 Entropy values of three different algorithms for pink noise
信息熵的有效性可以通过白噪声和粉红噪声噪声的信号规律进行评判,即白噪声信息熵值在各尺度下趋近于1,粉红噪声信息熵值会随着尺度因子的增加呈递减趋势。由图7可知,白噪声的多尺度模糊熵值随着尺度因子的增加先呈递减趋势后逐渐增大,熵值曲线波动幅度较大;白噪声的多尺度排列熵值较多尺度模糊熵稳定性有了显著的提高,但是熵值曲线也呈递减趋势,与白噪声的能量在整个频域范围内均匀分布的特点不符;白噪声的多尺度量子熵值在各尺度因子下基本保持不变,熵值曲线平稳,能够准确反映噪声信号的特点。由图8可以看出,粉红噪声的多尺度量子熵值曲线呈递减趋势,而另外两种熵值曲线较为平稳,鉴于粉红噪声的能量具有随着频率的增加而不断衰减的特点,因此多尺度量子熵的特征提取效果优于多尺度排列熵和多尺度模糊熵。
2.5 实验数据验证
采用美国西储大学轴承数据中心提供的滚动轴承试验数据,验证多尺度量子熵分析方法的泛化性。试验选用6205-2RS JEM SKF深沟球轴承,采用电火花技术分别对轴承设置不同程度损伤,损伤直径分别为0.177 8 mm,0.533 4 mm。在采样频率为12 000 Hz,转速为1 797 r/min的工况下采集不同种状态的振动信号,各20组数据,数据长度为4 096。首先对振动信号进行MQE分析,结果如图9所示。
由图9可知通过多尺度量子熵分析方法能够清晰地区分轴承正常工况和不同类型故障工况,为了进一步验证本文方法的泛化能力,选取正常工况和内圈、外圈、滚动体轻度故障4种工况各20组特征向量作为训练样本集,正常工况和内圈、外圈、滚动体中度故障各20组特征向量作为测试样本输入到训练好的PNN故障分类器中,测试样本输出结果如图10所示。

图9 7种不同状态下的振动信号多尺度量子熵Fig.9 MQE values over eight scales for analyzing 7 health bearing conditions
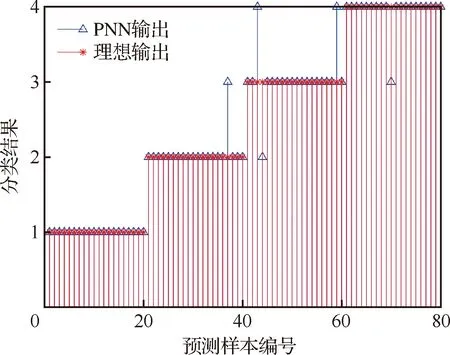
图10 PNN分类器输出结果Fig.10 Outputs of PNN classifier
由图10可看出,故障识别率为93.75%,共出现5个测试样本被误分,这说明基于轻度故障提取的故障特征样本训练的分类器能够对故障类型进行有效识别,具有良好的泛化能力。
3 中介轴承故障诊断实验分析
3.1 故障诊断模型
针对故障振动信号非平稳、非线性的特点,建立基于SCD、MQE、LLE和PNN的中介轴承故障诊断方法,其流程如图11所示。该方法首先采用空域相关算法对振动信号进行降噪处理;然后,利用MQE方法来提取各状态振动信号的故障特征信息,形成高维故障特征集;接着,采用局部线性嵌入算法对高维数据结构进行降维处理,保留数据本质特征的同时,实现故障特征信息可视化;最后,将低维故障特征输入概率神经网络中进行故障识别,实现故障智能诊断。

图11 中介轴承故障诊断模型Fig.11 Proposed fault diagnosis method for inter-shaft bearing
3.2 故障诊断实例
为了验证所提出的基于SCD、MQE、LLE和PNN故障诊断方法的有效性,搭建中介轴承故障模拟试验台如图12所示,采集沈阳航空航天大学中介轴承实验数据。

图12 中介轴承故障模拟系统Fig.12 Inter-shaft bearing fault simulation test system
实验采用6个加速度传感器,型号均为333B30。其中3个传感器灵敏度为98.6、99 mV/g和97.6 mV/g,安装在靠近低压电机的轴承座上,如图13(a)所示。其余3个安装于中介轴承的轴承座上,用于检测轴承3个方向的振动。灵敏度为99.3、98.3 mV/g和100.4 mV/g,安装位置如图13(b)所示。实验轴承采用NSK公司的NU202EM型号的圆柱滚子轴承,其具体结构参数如表1所示。

图13 加速度传感器布置Fig.13 Layout of acceleration sensors

表1 NU202EM轴承参数Table 1 Parameters for NU202EM bearing
为了模拟中介轴承的典型故障,采用线切割技术在中介轴承的内圈、外圈和滚动体的表面人工植入矩形表面缺陷,内圈故障和外圈故障的表面缺陷宽为0.5 mm,深为0.5 mm,滚动体故障表面缺陷尺寸深和宽皆为0.1 mm,带表面缺陷的中介轴承如图14所示。

图14 实验轴承Fig.14 Bearings used in experiment
实验设置中介轴承的工作状态为高低压转子反向旋转且高低压转子转速均为900 r/min,加速度传感器采样频率为16 384 Hz,采样时长为20 s。在此条件下,分别采集轴承正常工作(Normal)和具有内圈故障(IRF)、外圈故障(ORF)以及滚动体故障(BF)下的振动加速度信号各40组,4种类型共计160组样本,4种类型中介轴承的振动信号时域波形如图15所示。

图15 4种不同状态下的振动信号时域波形图Fig.15 Waveforms of inter-shaft bearing vibration signal under four different conditions
由图15可知,受背景噪声的影响,振动信号时域波形图曲线差异性不明显,故障征兆可能隐藏在噪声中,用传统快速傅里叶变换法难以识别不同类型的轴承故障。为了提取故障信息,首先采用空域相关降噪方法对不同状态下的振动信号进行处理,结果如图16所示。从图16可以看出,振动信号的时域波形图中冲击特征显著,验证了空域相关降噪算法能够降低噪声对振动信号的影响,进而便于清晰地提取出故障特征。

图16 降噪后振动信号的时域波形图Fig.16 Waveforms of inter-shaft bearing vibration signal after noise reduction
接着对降噪后的振动信号采用MQE算法进行特征提取,结果如图17所示。图17中可以看出,不同状态中介轴承的振动信号在不同的尺度因子下的MQE值不同,与故障轴承相比,正常轴承振动信号的多尺度量子熵值较小,且随着尺度因子的增大熵值曲线变化平稳,而故障轴承振动信号的多尺度量子熵值随着尺度因子的增大呈递减趋势。当=1时,4种状态下轴承振动信号熵值的大小关系是:MQE>MQE>MQE>MQE;当尺度因子增大到=16时,上述关系发生变化,此时4种状态下轴承振动信号熵值的大小关系是: MQE>MQE>MQE>MQE,这说明单一尺度的量子熵值无法完整地反映振动信号的全部信息,其他尺度下的时间序列也包含重要故障特征信息。综上,MQE能够有效地提取中介轴承振动信号的故障特征。

图17 不同故障类型下振动信号多尺度量子熵值Fig.17 MQE of vibration signals of different bearings
虽然MQE可以用来估计中介轴承振动信号的复杂性,但是仅通过观察MQE曲线来判别故障类型仍然是非常困难的。将从振动信号中提取出20个尺度的MQE作为特征向量,故障特征维数过大,会出现故障数据冗余,降低分类器的故障识别精度。因此,采用LLE算法对振动数据的故障特征进行降维,进而提升故障识别的效率和精度。为了实现融合数据的可视化,LLE的维度设置为=3。本文分别对6个振动传感器的故障特征进行融合降维,降维结果如图18所示。
根据类间可分性判据,同类样本的类内距离越小,异类样本子集合之间距离越大,表示数据的可分性越好,越适合作为故障特征向量。从图18中可以看出将高维MQE特征向量降维到三维后,各状态特征明显发生了分离。对比MQE的计算结果,可知利用LLE进行特征融合不但可以降低特征样本数据量,还可以提升故障特征向量的可分性。
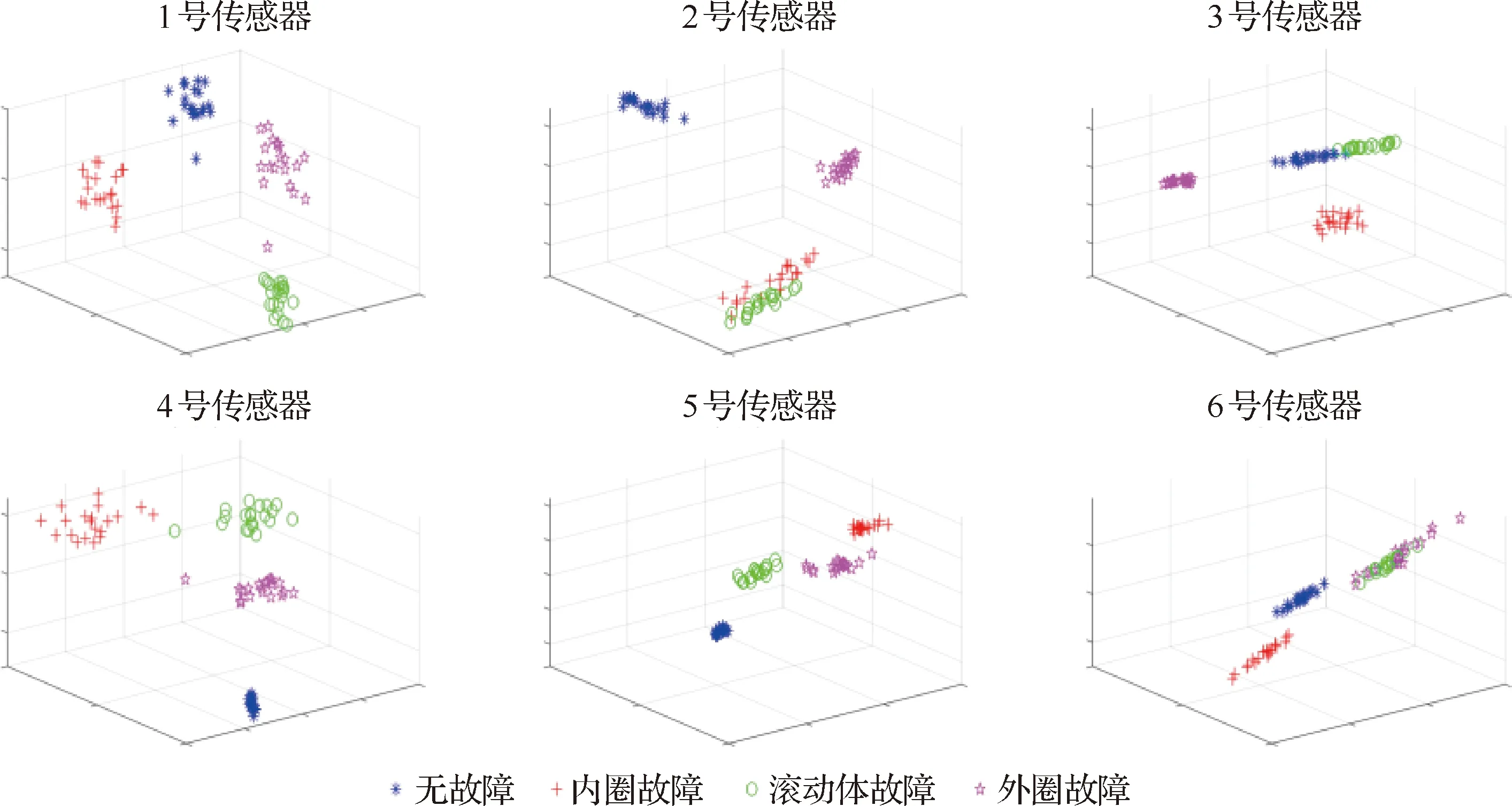
图18 不同传感器的LLE特征融合Fig.18 LLE feature fusion of different sensors
为了验证空域相关降噪算法的必要性,采用LLE对原始信号的MQE值进行特征融合降维,降维结果如图19所示。从图19可以看出,总体的类聚性较差,多个传感器的故障特征出现交叉重叠现象。因此,需要通过降噪算法来增强振动信号故障特征。最后,从每种状态随机抽取30个样本训练分类器,并将每种状态的40组样本用来测试。将1号、4号和5号传感器故障数据降维后的特征作为敏感故障特征输入到概率神经网络进行训练。采用建立的PNN模型对训练样本120组数据进行故障诊断,诊断结果如图20所示。然后,采用PNN分类器对测试样本160组故障样本进行诊断,诊断结果如图21所示。

图19 对原始信号进行LLE特征融合Fig.19 LLE feature fusion of original signal
从图20中可以看出,采用概率神经网络对于120组训练故障样本进行故障识别的准确率达到100%。对于训练故障样本能够完全分类正确,这可以说明概率神经网络具有良好故障分类性能,同时证明了该算法不容易出现过拟合现象。从图21中可知,PNN分类器对于正常轴承、外圈故障的诊断完全正确,滚动体故障中仅有1个被错误的诊断为内圈故障,内圈故障中有2个被错误的诊断为滚动体故障,故障样本的总体诊断准确率为98.12%。这证明本文所建立的算法可以有效地对中介轴承故障进行诊断。

图20 基于训练样本降维特征的PNN分类结果Fig.20 PNN classification results based on dimension reduction features of training samples

图21 基于测试样本降维特征的PNN分类结果Fig.21 PNN classification results based on dimension reduction features of test samples
最后,为了说明降噪和降维的必要性,选取原始信号的多尺度量子熵值、降噪处理后信号的多尺度量子熵值和对原始信号进行故障特征融合降维后的故障特征作为特征参数,分别通过概率神经网络进行训练和测试,输出结果见表2。由表2可得,本文所提方法高于其余3种特征提取方法的平均识别率,验证了SCD、MQE、LLE降维相结合的故障特征提取方法能够有效的提取出中介轴承故障类型的特征信息。
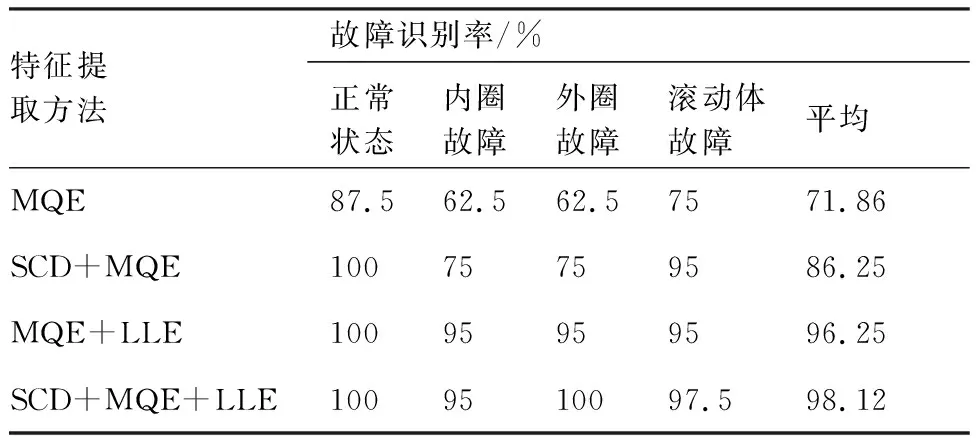
表2 PNN分类器对4种特征提取方法的故障识别率
4 结 论
1) 结合量子理论与信息熵理论,提出一种基于多尺度量子熵的特征提取方法。通过分析噪声信号,将MQE与MPE、MFE进行了对比,结果表明MQE能够更精确地提取振动信号故障特征信息,得到的熵值一致性和稳定性更好。
2) 将局部线性嵌入降维技术应用于高维故障特征降维,得到具有拓扑流形结构的低维可视化特征,采用LLE算法对高维的MQE进行降维融合后,不但降低了故障特征样本维数,还可以提升故障特征向量的可分性。
3) 提出了一种基于SCD、MQE、LLE降维技术和PNN的中介轴承故障诊断方法,实验结果表明,所提方法在信号降噪、故障特征提取、高维数据可视化降维和模式识别方面具有明显的优势,故障样本的总体诊断准确率达到98.12%。
