基于数字孪生的角磨机手工装配质量控制研究

厉丹丹

（杭州巨星科技股份有限公司，浙江杭州 310019）

角磨机是一种用于切削和打磨的磨具，可用于玻璃钢、金属和石材的切割和打磨。该磨具为手提式，其分为4寸、5寸、6寸、7寸以及9寸多种型号。角磨机在生产过程中，部分部件需要通过手工装配完成，装配效率和质量均依靠装配作业人员的技能水平和操作经验。在装配过程中，难免会发生漏装、混装以及装配顺序错误等情况[1]，此时，则需要将装配好的部分零件拆除，重新调整装配错误的零件，则会导致装配效率降低。如何提升角磨机手工装配的准确性，保证装配效率，成为装配管理的主要研究内容。

目前相关领域学者针对装配质量控制进行了研究，鞠萍华等[2]提出了一种基于偏最小二乘回归的运动机构装配质量关键控制点判定方法。根据“功能–运动–动作”的结构分解法，对元动作以及元动作链进行了定义。以元动作链上的最终元动作的输出运动参数为分析目标，采用状态空间和分层迭代方法，构造了元动作链的动态传递模型，并在此基础上，建立了各层次元动作的内部影响因子与装配质量的关系。使用偏最小二乘回归方法，对各个层次元动作中的影响因子进行了多元共线性分析，并采用变量投影重要性指数作为评价因子重要度的方法。通过对X轴进给运动状态下的单元动力链进行实例分析，表明这种方法可以对影响零件装配质量的因素进行有效的提取。李明等[3]提出了一种高精度电连接器自动化装配质量控制方法。本文利用自行设计的自感知自动组装实验平台，进行了电气连接器的自动组装实验，得到了电气连接件的主要技术参数，如位移–压装力曲线、最大压力分布等。根据组装工艺中的压装力变化趋势，对其产生的原因进行分析。通过对电连接器的大量实验和分析，提出了实现电气连接器自动组装的在线实时监测方法，控制电气接插件的组装质量。通过实践证明，采用该方法对装配过程进行参数监测是可行的。虽然上述方法均能够有效实现对装配质量的控制，但仍存在装配质量控制效率低的问题。

数字孪生作为一种映射方法，在产品制造、设计等多个领域中广泛应用，该方法具备数据映射、同步以及更新等特点，可实现物理实体的规划设计、状态监控等[4]。本文针对角磨机手工装配质量控制问题，将数字孪生用于质量控制中，精准掌控装配过程，多维度实现质量控制。

1 角磨机手工装配质量控制

1.1 基于数字孪生的装配质量控制模型

基于数字孪生的装配质量控制模型在对角磨机手工装配质量实行控制过程中，均具备装配过程质量状态的同步映射、在线监测以及反馈控制等多个能力，能够全面监控装配过程中的各步骤质量[5]，多维度和多尺度完成装配控制。装配质量控制模型结构如图1所示。

图1 基于数字孪生的装配质量控制模型

模型中的多维度包括角磨机装配过程可视化、装配参数计算以及数据映射等，对角磨机手工装配过程中的状态实行状态同步、计算、更新、分析以及装配管理；多角度是指产品、装配工序和车间等差异程度，通过构建各个尺度之间的关联模型，实现模型中多个功能的融合，完成角磨机手工装配质量的控制。

1.2 数字孪生模型的构建和参数同步

1.2.1 装配质量控制的数字孪生模型构建

本文构建的数字孪生模型，通过确定解析模型描述，模型中含有集总和分布两种参数，为完成物理车间和角磨机虚拟车间参数的对应[6]，需对上述两种参数中的线性部分，实行集中整合处理，并且未建模动态和分布特征的描述通过增广模型描述。

在实际应用中，对角磨机的物理实体输入力矩和控制数据实行采集，以此构建数字孪生装配质量控制模型，并且该模型中运动部件的等价系统，采用时间平稳序列进行表示。采用自回归滑动平均模型描述基于数字孪生的角磨机手工装配质量控制模型，其公式为：

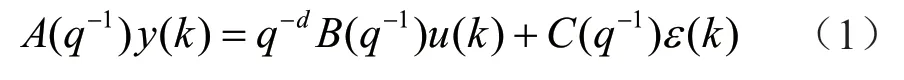
式中：ε（k）表示白噪声；A（q-1）y（k）表示时间序列；B（q-1）、C（q-1）表示实系数多项式；u（k）表示协方差函数；q-d为待定系数。

1.2.2 基于最小二乘的参数同步

角磨机手工装配作业环境和操作人员的差异，均会导致数字孪生的装配质量控制模型，在控制过程中发生参数退化情况，为了保证虚拟车间模型和实际物理实体之间的一致性，可靠生成物理镜像，采用最小二乘算法完成模型的更新，更新流程如图2所示。

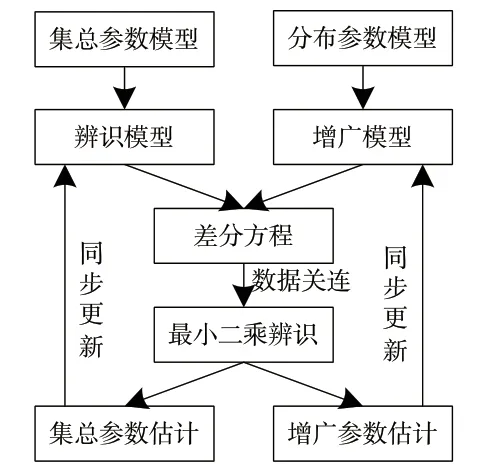
图2 最小二乘算法的模型参数同步

参数同步需以集总和非线性两种参数为基础，提取两者中的装配特性参数和状态参数，将提取的参数作为关键参数用于辨识模型。通过增广模型表示未建模动态和噪声，提升装配过程的辨识精度[7]。在此基础上构建差分方程，以及最小二乘辨识完成集总和非线性两种参数的估计，实现装配模型参数的更新和同步。

1.3 基于Copula函数相关性的装配质量控制

完成模型参数更新、同步后，实现角磨机实体和模型之间的映射，采用基于Copula 函数确定映射模型的质量控制点，结合相关性的多元质量控制图实现装配过程质量控制。

质量控制点是角磨机在手工装配过程中的一个装配规范，其对于角磨机手工装配质量存在直接关联；该关联的描述采用相关性模型描述，且该模型依据Copula 函数构建。如果装配工序用Zi表示，角磨机手工装配过程中需按照规定的工序完成，并且装配的前后工序之间会相互影响[8]，导致最终的装配质量受到影响。质量控制点之间的相关性模型建立步骤如下：

（1）分析装配完成且质量合格角磨机的历史质量控制点数据，并对前后质量控制点的边缘分布函数实行估计。

（2）分别完成频数和频率两种直方图的绘制，以该图形的特点为依据，确定Copula 函数。

（3）对Copula 函数的未知函数实行估计。

（4）获取函数模型中的最佳函数和该函数对应的概率密度函数f（xi），其通过评价的方式完成。

依据上述步骤即可完成质量控制模型的构建，通过该模型分析各个质量控制点之间的关联性，在此基础上，采用标准化多个质量点数据的整合处理，实现数据多元的转换，形成一元数据；对该数据的统计过程实行控制，即完成多元质量的控制，完成角磨机手工装配质量的控制。

数据的整合处理采用公差分析法完成，其转换公式为：

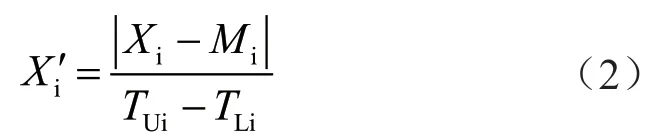
式中：Xi表示原始数据；TUi、TLi分别表示角磨机手工装配质量控制的上限值和下限值；Mi表示角磨机手工装配质量控制的目标值；Xi'表示转换后的质量数据。

基于上述内容，完成基于Copula 函数相关性的多元质量控制图构建，实现角磨机手工装配质量控制。

2 实验结果分析

为测试所提方法的应用效果，以某角磨机生产企业为测试对象，采用所提方法对其手工装配实行控制，获取所提方法的控制结果。

为测试所提方法对于装配过程质量控制性能，采用同心度偏差作为衡量标准，获取所提方法在不同的噪声下装配质量控制结果，如图3所示。同心度偏差结果的期望标准低于0.16。

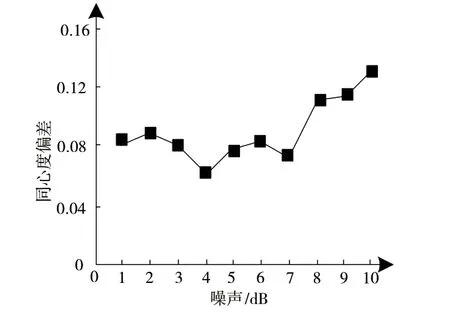
图3 装配质量控制结果

依据图3测试结果可知：所提方法在不同噪声下，对角磨机手工装配实行控制后，同心度偏差结果均在0.16以下，表示所提方法对于角磨机手工装配质量控制性能良好，能够保证最后的装配质量。

在此基础上，进一步验证所提方法的角磨机手工装配质量控制效率，将装配质量控制时间作为评价指标。其装配质量控制时间越短，表明装配质量控制效率越高。分别采用文献[2]方法和文献[3]方法与所提方法进行对比，得到不同方法的角磨机手工装配质量控制时间对比结果如表1所示。

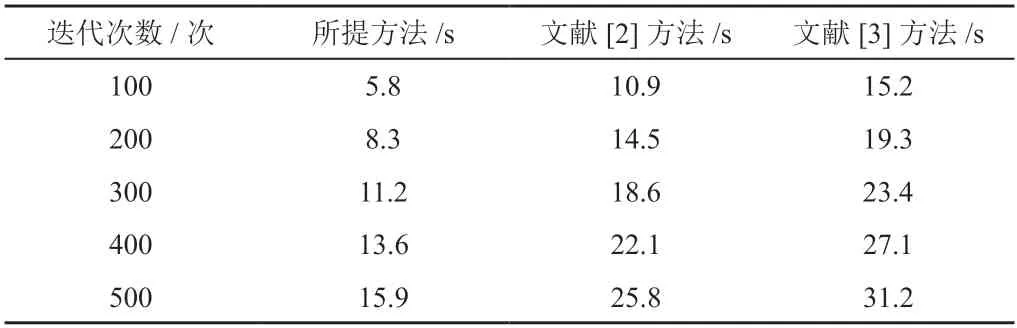
表1 不同方法的角磨机手工装配质量控制时间对比结果

依据表1测试结果可知：随着迭代次数的增加，不同方法的角磨机手工装配质量控制时间随之增加。当迭代次数为500次时，文献[2]方法的角磨机手工装配质量控制时间为25.8 s，文献[3]方法的角磨机手工装配质量控制时间为31.2 s。而所提方法的角磨机手工装配质量控制时间仅为15.9 s。由此可知，所提方法的角磨机手工装配质量控制时间较短，能够有效提高角磨机手工装配质量控制效率。

3 结论

角磨机装配质量直接影响其使用情况，装配质量如果过差，则会导致产品无法使用，因此本文研究基于数字孪生的角磨机手工装配质量控制方法。该方法利用数字孪生的优势完成孪生装配车间的映射，并实时完成角磨机实际装配数据的采集，通过装配质量控制点的控制，分析各个质量控制点之间的关联性，基于Copula 函数相关性的多元质量控制图，完成角磨机手工装配质量控制。测试结果表明，所提方法的控制性能较好，能够满足角磨机手工装配质量控制的需求。