基于ITD-FE-SVD的水轮发电机组振动信号去噪方法
2022-09-08胡雷鸣丁岳平洪福文袁长征
胡雷鸣,黄 卉,丁岳平,洪福文,袁长征
(江西洪屏抽水蓄能有限公司,江西省宜春市 330600)
0 引言
随着国际能源结构的调整优化,各国现在都在大力发展新能源技术,而在新能源发电方面水力发电相对于风力发电和太阳能发电等其可利用率相对来说更高,所发可利用电能更加稳定,并且响应迅速,能够短时间达到电网所要求的负荷,具有调峰调频、黑启动的效应。但在水力发电中最为重要的就是水轮发电机组,其状态的好坏对机组能否安全稳定运行起着决定性的作用。根据相关研究显示,水轮发电机组的故障状态80%能够从其振动数据中显示[1,2]。所以,对那些易被噪声干扰导致机组频率特征难以提取的振动数据进行消噪,去除噪声的干扰,准确提起其振动频率,及时掌握机组的运行状态,就显得很重要。
目前国内常用的信号分解方法有小波分解、经验模态分解和局部均值分解等,但这些方法都有其局限性,例如,小波分解受其小波基的选取会影响其分解精度,经验模态分解和局部均值分解在分解过程中会出现模态混叠等现象。而固有时间尺度分解[3](intrinsic time scale decomposition,ITD)不使用样条曲线来适应局部极值,因此,它不受样条插值到信号包络的过冲和下冲误差的影响,在抑制末端效应和模态混合方面效果更好,从而避免可能产生的伪极值以及可能产生虚假的极值和偏移。此外,它不涉及PRC分离中的复杂筛选过程,因此,具有低计算复杂度,能避免由于重复筛选导致的瞬态和时间尺度拖尾的平滑。在瞬时参数估计方面,ITD基于单波分析定义PRC的瞬时幅度和瞬时频率,从而能够克服传统希尔伯特变换方法的缺点,如末端效应、瞬时频率尖峰和负频率值。文献[4]提出一种固有时间尺度分解和傅里叶变换相结合的滚动轴承数据分析方法,对故障数据进行去噪再提取轴承故障的特征频率,对滚动轴承故障进行了准确预判[4]。
模糊熵(fuzzy entropy,FE)与样本熵和近似熵类似,可以用来计算时间序列复杂度,随着时间序列维数产生的变化来衡量新模式概率的大小。当信号为纯信号时,其时间序列自我相似性就会很高,熵值就会很小,当信号中受到噪声干扰时,其模糊熵值也会随着变大[5-8]。
奇异值分解(singular value decomposition,SVD)在信号分析领域具有相当广泛的应用,其去噪原理是在相空间的基础上,通过对相关矩阵实现奇异值分解。由于噪声成分和实际信号成分之间的相关性不同,噪声成分在通过奇异值分解后其奇异值的变化率较小,而且其能量值也很小,有效信号成分奇异值能量值贡献大,所以,奇异值变化的斜率就很大,可以根据奇异值变化斜率的大小和其能量值来判断噪声和有效信号[9-12]。文献[13]基于SVDMEEMD与Teager能量谱的滚动轴承微弱故障特征提取方法,成功实现了对早期故障的特征提取。
本文结合这3种算法的特点和优势提出ITD-FE-SVD水轮发电机组振动信号去噪方法,利用ITD先对振动数据进行分解以模糊熵为阈值,选取含噪量较小的分量进行重构,达到第一次去噪的效果;再在这个去噪的基础上进行SVD分解,根据奇异值差分谱中奇异值变化较大的点来选择重构阶数对数据进行重构,从而达到几乎完全去噪的效果。
1 固有时间尺度分解[3,4]
对于水轮发电机组振动信号x(t),定义基线提取算子L以分离较低频率基线信号,即Lx(t)表示信号的瞬时均值,写为L(t);将Hx(t)=x(t)-L(t)定义为正确的旋转分量,写为H(t),然后信号可以分解为x(t)=L(t)+H(t)。基于以上定义,ITD算法详述如下。
步骤1:求出信号x(t)的极值,写为xk,以及相应的发生时刻nk,k=0,1,2,…,不失一般性,让n0=0。

2 模糊熵原理


3 奇异值差分谱原理


4 水轮发电机组振动信号仿真分析
4.1 机组的振动仿真信号
根据水轮发电机组振动信号的组成一般为机组的转频、机组倍频和其他一些频率,并且各个频率之间的幅值都各有差异这一关系。设置仿真函数x1由机组的转频1Hz、0.4倍频、3.5倍频和7.2倍频组成,并且各个频率的幅值之间设置有差值。x2为高斯白噪声。数据的采集频率为500次/s,采集5000个数据进行分析。图1为仿真不加噪数据波形图,图2为仿真数据加噪波形图。可以发现,由于高强度噪声的影响,原有振动信号的波形几乎被噪声淹没,这对准确提取振动数据信号特征,判断机组的运行状况影响较大。

图1 仿真不加噪波形Figure 1 Simulation without noise waveform
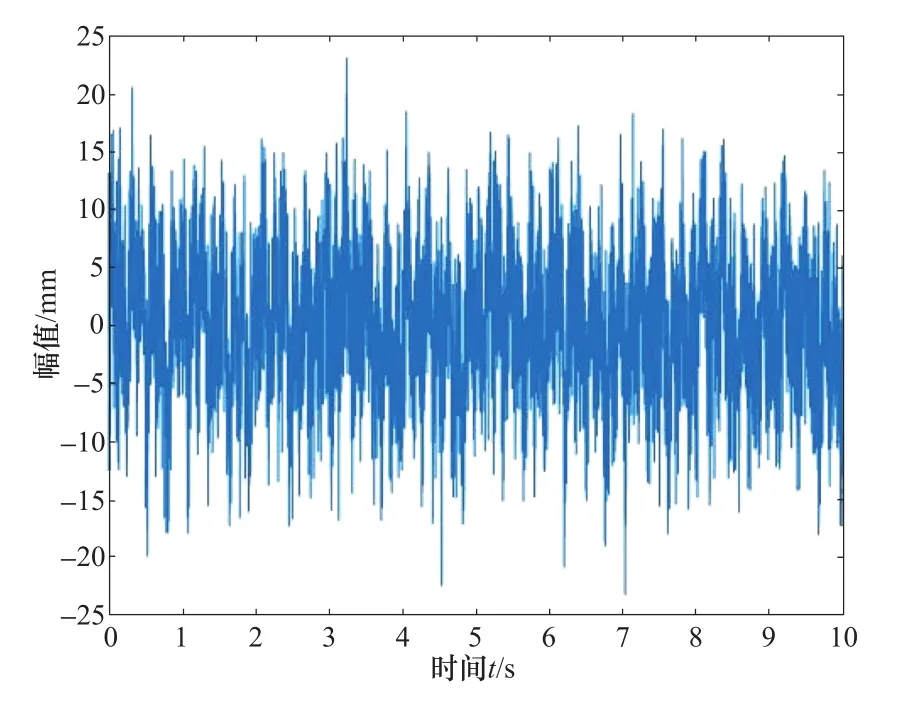
图2 仿真加噪波形Figure 2 Simulation of noise addition waveform
4.2 固有时间尺度分解
将仿真振动信号进行ITD分解,分解后得到7个PRC分量如图3所示。观察7个分量可以发现,前2个分量数据的波形图杂乱无章,类似于噪声信号波形;后5个分量的波形较规则、平整、圆滑,类似实际数据的振动信号波形。通过计算7个分量的模糊熵如表1所示,根据模糊熵的定义可知,信号的自我相似性越高时,其值越小。信号中含有噪声时,其值变大。前2个分量的值相对来说比较大,并且其波形也呈现为噪声类波形。但为确定模糊熵阈值,确保所去除部分几乎全部为噪声,留下更多的有用信号,保证去噪后所得的振动数据完整性。通过多次仿真实验,设定模糊熵阈值为2。将模糊熵值大于2的分量舍弃,选取后6个分量进行重构。重构后数据的波形频率图如图4所示。

表1 各PRC分量模糊熵Table 1 The fuzzy entropy of each PRC component
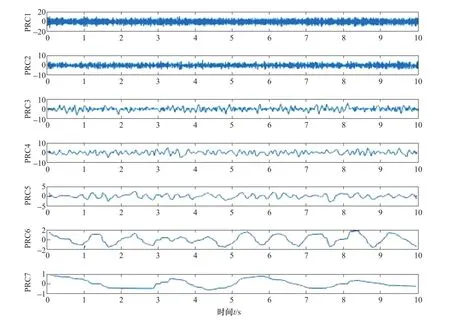
图3 仿真信号ITD分解各分量波形图Figure 3 Waveform diagram of each component of simulation signal ITD decomposition
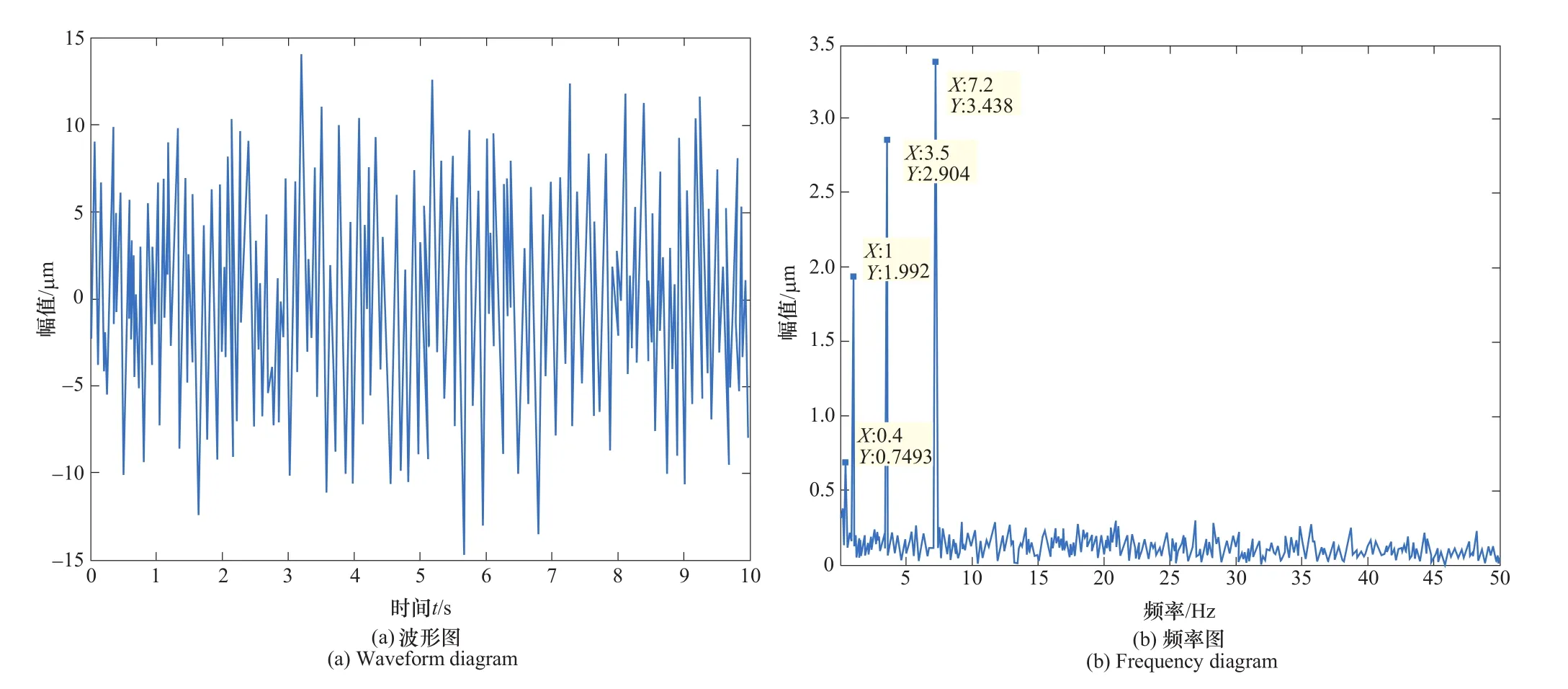
图4 ITD-FE去噪后信号波形频率图Figure 4 The frequency diagram of the signal waveform after ITD-FE denoising
将模糊熵去噪后的数据波形图和仿真不加噪波形图进行对比发现,经过ITD-FE去噪后,振动数据中还是含有比较多的噪声,去噪后的波形和仿真不加噪波形之间相差较大。并且观察其频率图也可以发现,经过ITD-FE去噪后,机组仿真所设置的4个频率能够被准确地提取出来,但频率图中还夹杂着很多噪声频率。为对振动信号数据进行进一步的消噪处理,将经过ITD-FE去噪后的振动数据进行奇异值分解,得到奇异值差分谱如图5所示。红色线为奇异值差分谱,蓝色线为奇异值变化的曲线,可以发现奇异值在8的时候变化比较大,到9的时候变化就变得比较小了,而且奇异值差分谱中阶次为8的时候其能量值也很大,所以选择重构的阶次为8。得到重构后的数据波形频率图如图6所示,可以发现波形图几乎和仿真不加噪波形一模一样,仿真所设置的4个频率也被完整地提取出来,频率的副值偏差也都小于10%,并且噪声频率几乎为零。说明,经过固有时间尺度分解模糊熵和奇异值相结合的方法,能够有效地去除振动信号中的噪声。
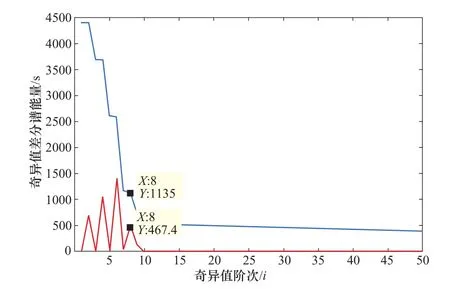
图5 奇异值差分谱图Figure 5 Singular value difference spectrum
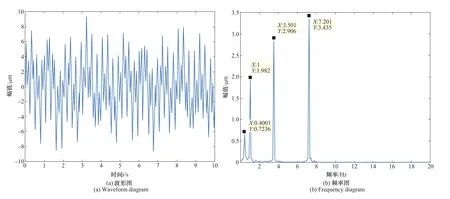
图6 奇异值去噪后数据波形频率图Figure 6 Data waveform frequency diagram after singular value denoising
4.3 局部均值分解
将仿真信号导入到局部均值分解中进行自适应分解,分解后所得7个分量的波形图如图7所示,各分量的模糊熵见表2。根据前面所设置的模糊熵阈值2,选择小于2的后6个分量进行重构,重构后数据的波形图和频率图如图8所示。经过LMD-FE去噪后的数据中,相对来说还含有较多的噪声,其波形图中能够明显看到噪声那种杂乱无章的波形,而且频率图中含有的噪声频率也相对来说很多,并且幅值很大。将LMD-FE去噪后的数据进行奇异值分解,其奇异值谱如图9所示。观察奇异值变化和奇异谱能量值也可以发现,奇异值在8及8之前变化都比较大,到9及9之后的时候变化就变得比较小了,而且奇异值差分谱中阶次为8时能量也很大,所以设置重构的阶次也为8。得到重构后的数据波形频率图如图10所示,可以发现,波形图几乎和仿真不加噪波形一模一样,仿真所设置的4个频率也被完整地提取出来,频率副值偏差也都小于10%,并且噪声频率几乎为零。说明,经过局部均值分解模糊熵和奇异值相结合的方法,也能够有效地去除振动信号中的噪声。
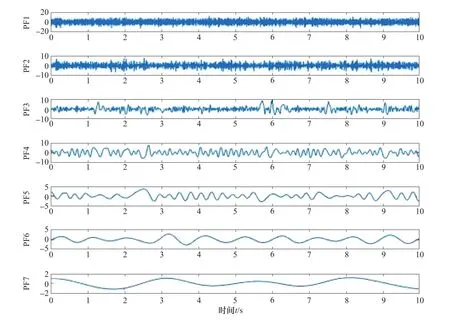
图7 LMD分解各分量波形图Figure 7 LMD decomposition waveform diagram of each component
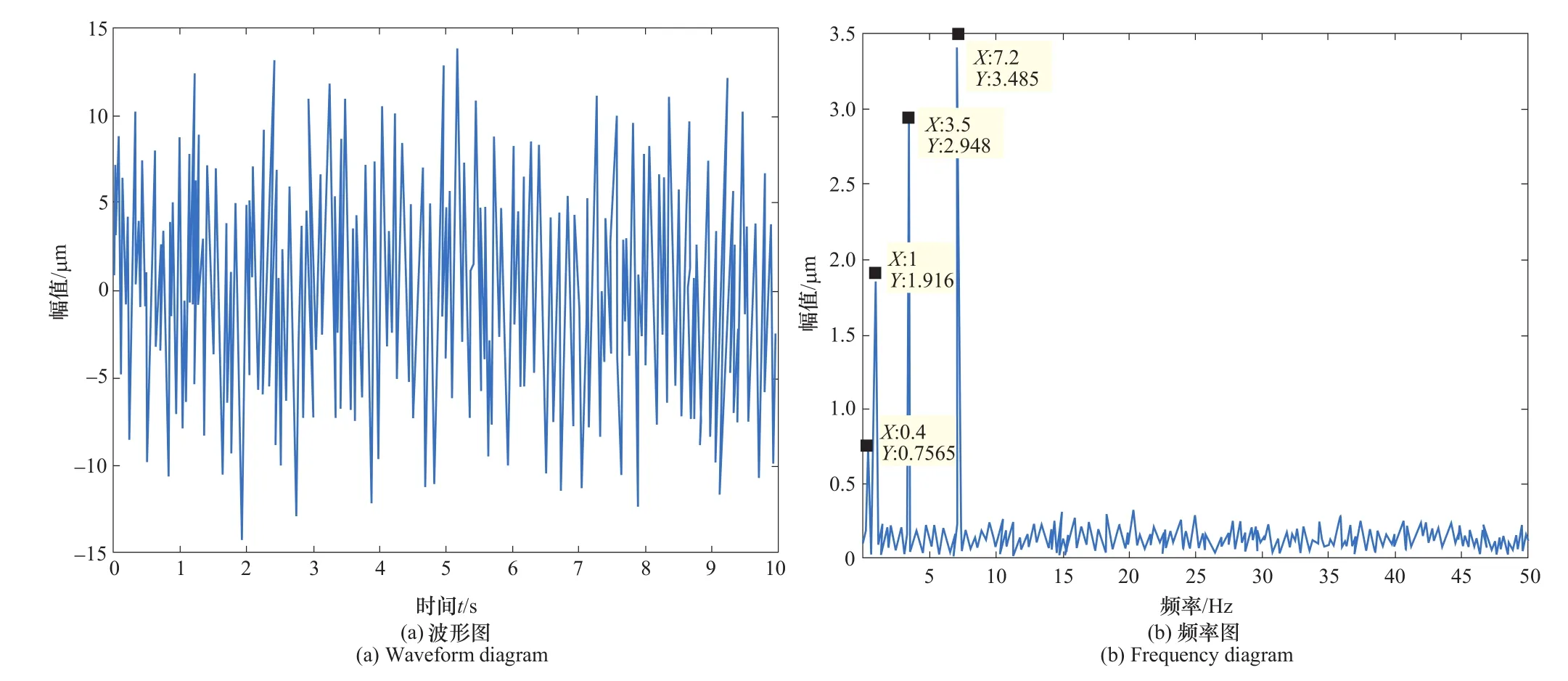
图8 LMD-FE去噪后信号波形频率图Figure 8 Signal waveform frequency diagram after LMD-FE denoising
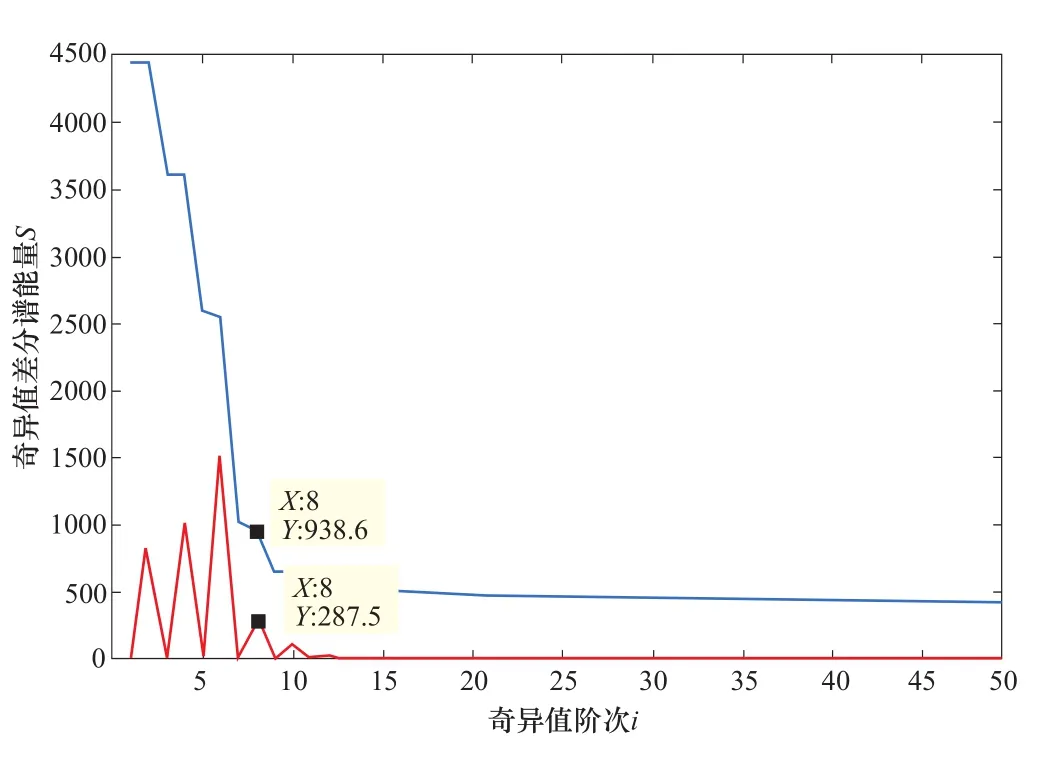
图9 奇异值差分谱图Figure 9 Singular value difference spectrum
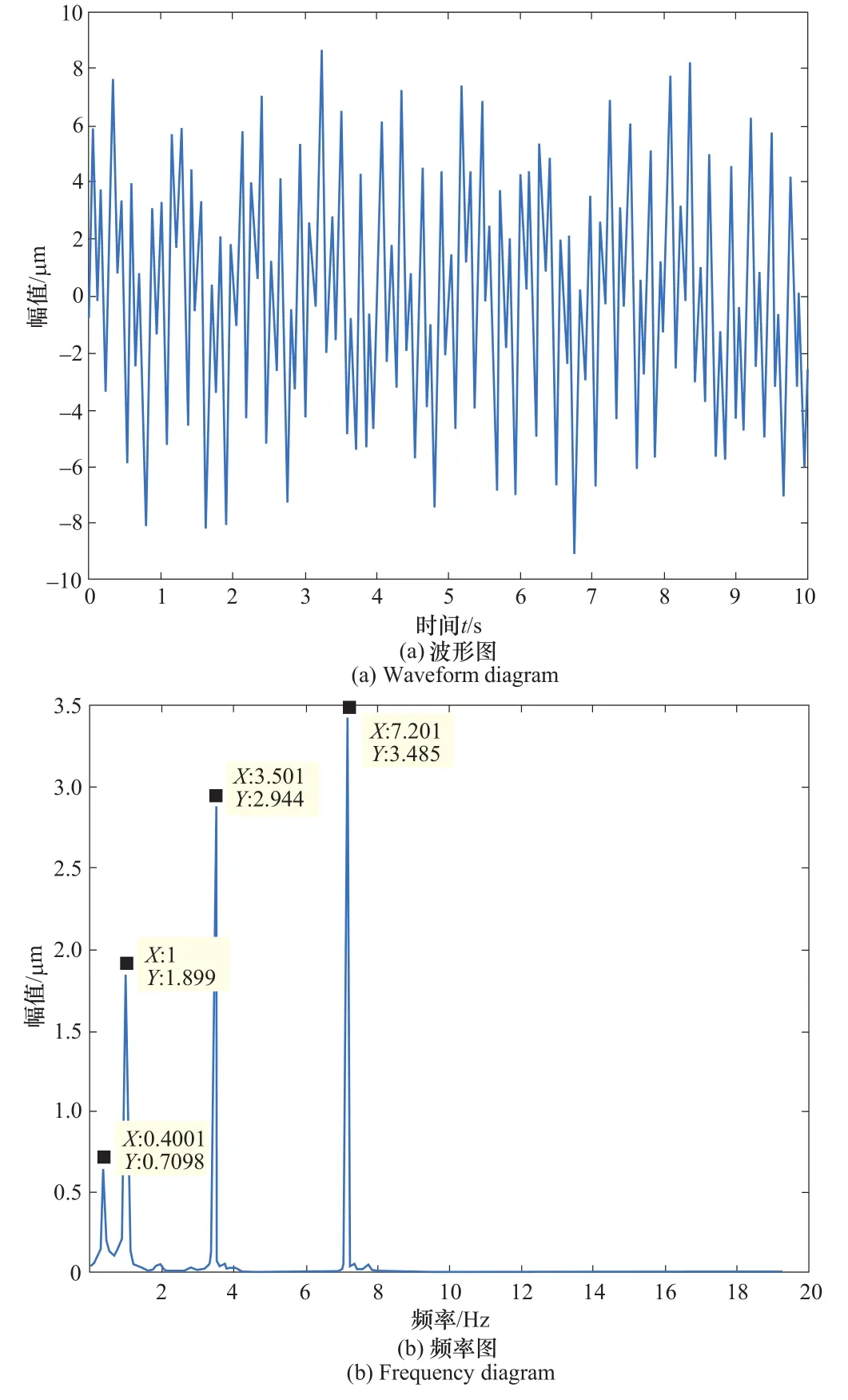
图10 奇异值去噪后数据波形频率图Figure 10 Data waveform frequency diagram after singular value denoising

表2 各PF分量模糊熵Table 2 The fuzzy entropy of each PF component
4.4 相关指标比较
经过上面的分析可以发现,不论是ITD-FE-SVD相结合的水轮发电机组振动数据去噪方法,还是LMD-FESVD相结合的水轮发电机组振动数据去噪方法,都能够有效地去除振动数据中的噪声。为凸显出本文所提方法的优越性,将去噪后的数据和原始仿真数据进行相关性分析和信噪比分析[14],结果见表3。发现,经过ITDFE-SVD去噪后数据的相关系数为0.9968,信噪比为21.687相对来说都更高,说明ITD-FE-SVD这种振动数据的去噪方法能够更有效地清除噪声,并且保留更多原信号中的有用信息。
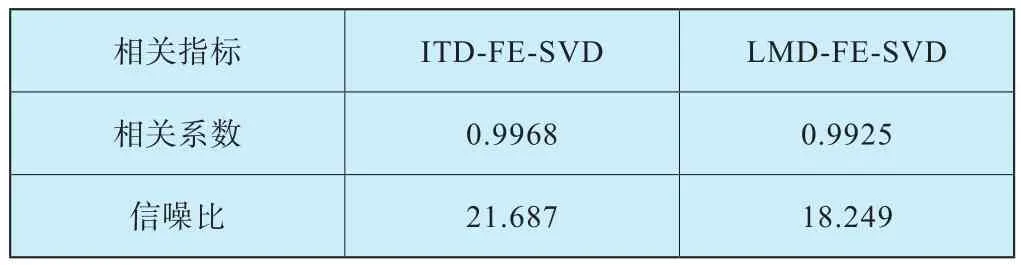
表3 相关指标Table 3 Related indicators
5 机组振动数据验证
为验证ITD-FE-SVD这种方法在实际电站机组振动数据中的有效性,选取某电站机组的振动数据进行分析,其中,采集时机组转速为136r/min。数据采集频率为500Hz,从中随机选取5000个数据进行分析。机组上导X向的振动数据波形和频率图如图11所示,由于噪声的影响频率图中出现了很多干扰噪声信号,这对准确提取振动信号故障特征判断机组的运行状况有较大的影响。

图11 机组振动数据波形频率图Figure 11 Frequency diagram of unit vibration data waveform
将机组的振动数据进行ITD分解,分解后各分量的波形图如图12所示,各分量的模糊熵值如表4所示,选取小于2的后6个分量进行重构,重构后数据的波形和频率图如图13所示。经过ITD-FE去噪后机组振动数据中大部分的噪声得到了清除,但通过其频率图可以发现,其中还是遗留有小部分的噪声。将经过ITD-FE去噪后的振动数据进行奇异值分解,分解后奇异值差分谱图如图14所示。奇异值在6~7之间也就是6的时候变化还比较大,到7以后奇异值的变化就变得比较小了,并且在6的时候奇异值的能量值也很大,所以选择重构的阶次为6。重构后数据的波形和频率图如图15所示,机组的振动数据波形图显得非常光滑、圆润,没有噪声的干扰,并且其频率图中也几乎没有了噪声频率,说明本文该方法能够很好地去除实际机组振动数据中的噪声。

表4 各PRC分量模糊熵Table 4 The fuzzy entropy of each PRC component

图12 ITD分解后各分量波形图Figure 12 Waveform diagram of each component after ITD decomposition

图13 ITD-FE去噪后数据波形频率图Figure 13 Data waveform frequency diagram after ITD-FE denoising

图14 奇异值差分谱图Figure 14 Singular value difference spectrum
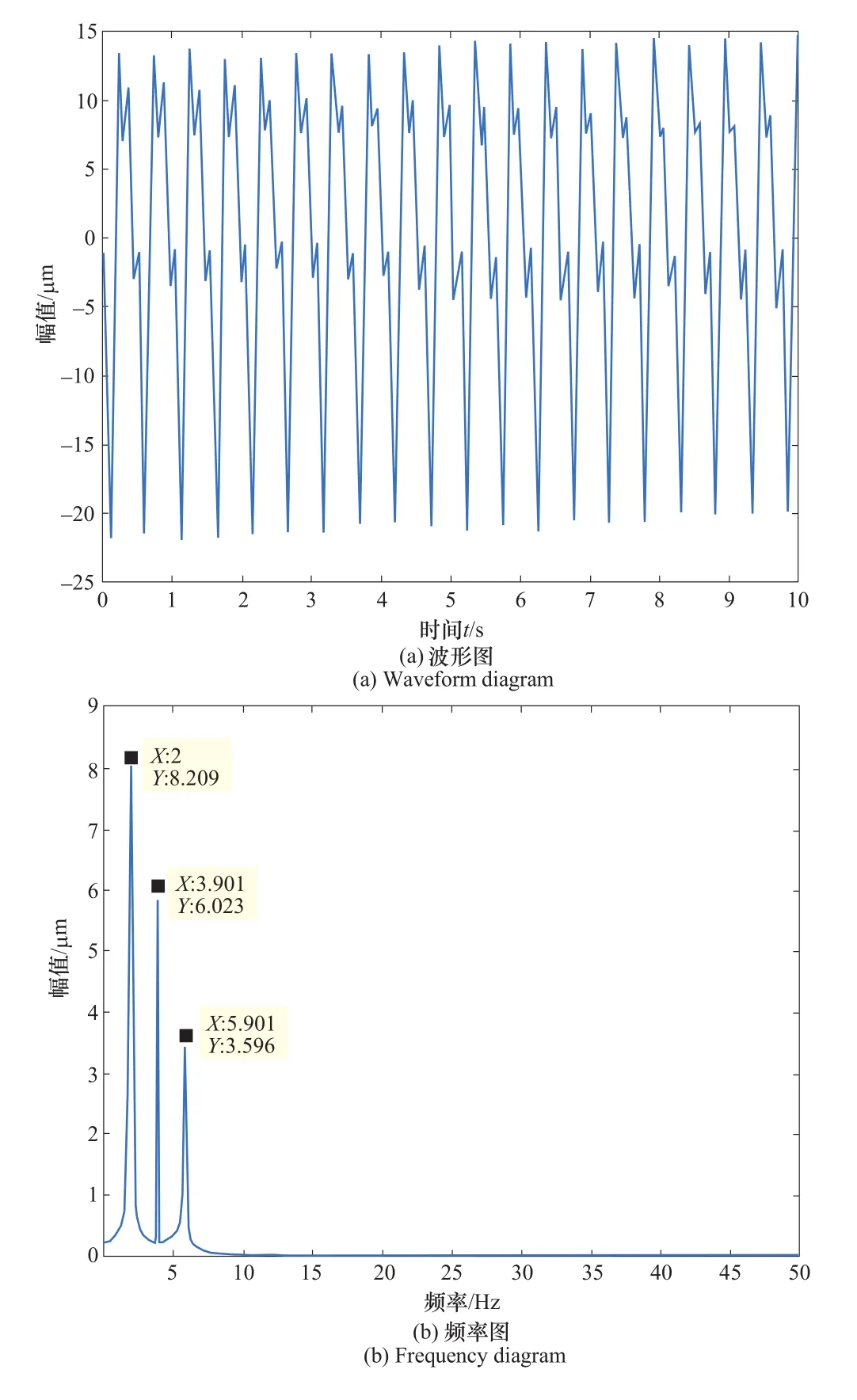
图15 ITD-FE-SVD去噪后数据波形频率图Figure 15 Data waveform frequency diagram after ITD-FE-SVD denoising
6 结语
(1)本文结合ITD、FE、SVD这3种方法的优势和特点提出一种ITD-FE-SVD的水轮发电机组振动数据去噪方法,经过仿真验证了该方法的有效性。并将该方法和LMD-FE-SVD方法对比发现,本文该方法去噪效果更好,能够更多地保留原信号的有用信息。
(2)将ITD-FE-SVD用于实际机组振动数据去噪,发现本文该方法能够有效地去除机组振动数据中的噪声,为下一步准确提取振动数据的振动频率,判断机组的运行状态,具有非常大的作用。
