水头大变幅水泵水轮机研制
2022-09-08刘德民赵永智方玉建许唯林陈泓宇黄晓东魏炳章
刘德民,赵永智,方玉建,许唯林,陈泓宇,黄晓东,魏炳章,林 凯
(1.东方电气集团东方电机有限公司,四川省德阳市 618000;2.四川大学,四川省成都市 610065;3.温岭市产品质量检验所,浙江省温岭市 317599;4.南方电网调峰调频发电有限公司,广东省广州市 510600)
0 引言
近年来,我国抽水蓄能装机规模快速增长,截至2021年12月,抽水蓄能在运规模已达3249万kW,在建规模达3871万kW。根据国家发展改革委《关于促进抽水蓄能电站健康有序发展有关问题的意见》,2025年抽水蓄能装机容量将达到6200万kW以上,到2030年,抽水蓄能投产总规模将较“十四五”再翻一番,达到1.2亿kW左右。由此可见,抽水蓄能电站在未来有着广阔的发展前景。
在抽水蓄能机组中,高水头水泵水轮机具有转速高、水位相对波动小等特点,且在同等功率条件下通过高水头机组的流量较小,机组的尺寸减小,有助于减少电站造价[1]。高水头化是水泵水轮机的发展趋势。在日本、美国和瑞士等国家,水泵水轮机的研究起步较早,抽水蓄能装机容量普遍在8%以上。我国抽水蓄能的装机规模略低,仅占1.5%。我国抽水蓄能的发展向着高水头、大容量、高转速的方向发展。目前抽水蓄能单机容量已达400MW,水头已经达到780m,转速已经达到600r/min。
20世纪90年代,日本大部分抽水蓄能电站的最高水头都在500m以上,其中葛野川电站的最高水头达到779m。国内最高水头的长龙山电站水头已经达到了760m,敦化抽水蓄能机组最高水头达到了712m,图1为目前国外主要水泵水轮机机组水头发展趋势的统计[2]。
1 研究进展
需要指出的是,抽水蓄能电站担任调峰任务,实际运行中机组需经历抽水、发电等多个工况的快速转换,这对机组各个工况下启动的稳定性提出了很高的要求。特别是机组高水头化后,水头运行范围更加宽广,由高水头机组大变幅(变幅超过15%)引起的稳定性问题更严重。压力脉动是影响水泵水轮机尤其是高水头机组运行稳定性的主要因素。快速而频繁的工况转换及水头变化,偏工况的运行需求等都对高水头水泵水轮机提出了严峻的技术挑战。其机组内部复杂三维湍流产生的压力脉动现象几乎在所有运行工况出现,是机械振动和疲劳的主要源头。因此,压力脉动对水泵水轮机运行稳定性至关重要。在泵工况机组启动过程中,部分工况会导致机组输入功率剧烈变化,继而导致输水系统剧烈振荡,甚至导致机组跳机,严重时可能造成机组或输水系统的破坏[3]。水轮机工况方面,某些流态诸如转轮进口回流、无叶空间内稳态涡的出现(绝对不稳定工况下存在诸多强烈不稳定漩涡结构,即具有分离的小尺度多涡丝强螺旋涡带结构)和旋转失速,特别是在无负荷转速条件下,上述这些问题在水轮机工况下都可以在某些工况对水泵水轮机组运行稳定性造成不可忽略的影响[4,5]。此外,随着水头的提高,机组转速的提高、内部流速加大,空化现象将变得越发严重,从而对机组的开挖深度提出更高的要求。由此看来,高水头水泵水轮机的空化问题不容忽视。Fisher的试验研究结果指出[6],水泵水轮机的空化现象对机组性能有着显著的影响;刘锦涛[7]在数值模拟水泵水轮机水泵工况的内部流场时,与单向流计算相比,引入空化模型的数值计算结果更接近试验结果。
1.1 水泵水轮机压力脉动
压力脉动的数值研究等方面,根据文献调研发现,水泵水轮机无叶区内转轮倍频下的压力脉动是导致机组和厂房振动等一系列安全隐患的直接原因[8-11]。国内外专家针对水泵水轮机压力脉动问题进行了源头分析、幅频特性分析、周向和径向传播规律分析等一系列研究,并取得了一定的研究成果。
刘树红等人[12]利用 SSTk-ω模型详细分析了水泵水轮机压力脉动的传递规律。研究发现,在整个无叶区范围内,压力脉动的主频均为叶片的通过频率。肖若富等人[13]分析了水泵水轮机在预开导叶启动过程中的压力脉动特性,在预开导叶后压力脉动相对幅值大幅增加,且主频频率也因预开开度不同而不同。尹俊连等人[14]利用DES模型数值计算额水泵水轮机在泵工况下的压力脉动并进行了频域和时域分析。研究发现,在固定导叶内部,低频压力脉动分量占主导,此分量主要是由活动导叶进口处的流动分离引起的。Staubli等人[15]利用计算分析了无叶区和转轮入口处的流量变化,发现无叶区处的低频压力脉动与转轮进口处周期性出现与消失的失速团息息相关。Roth等人[16,17]分析了水泵水轮机内部流场的动静干涉特性。研究发现活动导叶的振动对无叶区内的压力脉动也有一定的影响;以活动导叶为界线,上下游区域距离活动导叶越近,压力脉动的幅值就越大。Hasmatuchi等人[18,19]利用模型机试验分析了在机组启动过程中压力脉动的变化规律。研究发现,在水轮机工况下,越是靠近无叶区,压力脉动幅值就越大。
Li等人[20]针对宝泉抽水蓄能电站中原型水泵水轮机的压力脉动、摆度和振动等参数进行试验。试验结果表明:机组振动和摆度信号中的主频均为叶轮旋转频率。Egusquiza等人[21]对一些抽水蓄能电站中的原型水泵水轮机15年来的振动数据进行了分析,重点分析了振动激振力的来源。分析结果表明:水泵水轮机的振动水平比传统的水轮机要高出许多,主要原因是水泵水轮机的导叶和转轮之间的强烈的动静干涉作用产生了高幅度的压力脉动。压力脉动的频率取决于导叶和转轮叶片数量的结合,并且振动水平与运行的工况密不可分。
1.2 水泵水轮机湍流模型研究
目前针对水泵水轮机内部湍流的数值模拟方法大致可以分为三类:直接数值计算方法(DNS)、大涡模拟(LES)和雷诺平均法(RANS)。其中DNS 和LES 对网格的要求高,计算量大,目前不适用于大型水力机械非定常流动的数值计算;RANS 对N-S方程进行雷诺时均化,通过引入湍流模型来封闭方程,计算量要求相对较低、应用相对较广。RANS方法中的大部分湍流模型为线性模型,对复杂的非线性流动进行模拟具有一定的局限性。
研究表明,非线性湍流模型中的V2F 模型表现出了对复杂流动的良好模拟效果,该模型最早由Durbin[22]提出,采用速度尺度函数代替湍动能来计算涡黏系数,并考虑了近壁湍流的各向异性及局部压力和应变率的影响,直接模拟近壁区流动[23]。
V2F 模型可以对复杂流动中的近壁区分离流动进行较为准确的模拟,并且有机会捕捉到回流和失速等流动现象[24]。考虑到在水泵水轮机近壁区的分离流以及回流、失速等现象可能起着重要作用,V2F 模型作为RANS 方法,对复杂流动的模拟具有强大优势。由于水泵水轮机复杂工况流动中存在近壁面的回流、失速等非线性现象,考虑对大尺度涡的模拟和对计算资源的需求,本文的优化计算分析基于V2F 湍流模型完成高水头水泵水轮机内部复杂湍流的非定常计算研究。
1.3 水泵水轮机空化数值研究
空化问题是制约高水头扬程大变幅水泵水轮机发展的关键因素之一。为了避免空化效应引起的负面影响,如效率降低、压力脉动及振动和空蚀等,水泵水轮机在设计上要考虑满足相应的空化余量。因此,对水泵水轮机组空化性能的精确预测十分重要。
空化研究的理论方面,空化模型用于描述空化多相流各相间的质量传输特性,分为拉格朗日法和欧拉法,其中拉格朗日法包括气泡追踪法和界面追踪法,欧拉法包括双流体模型和混合流体模型。目前欧拉法使用较广泛,其中双流体模型将液相和气相考虑为彼此独立而又相互作用的流体进行计算,计算工作量较大。在双流体模型的基础上,混合流体模型开始得到发展。这种空化模型把流场中的气体和液体视为混合物,只对混合流体的连续方程、动量方程和空泡相的体积组分方程进行求解,其中体积组分方程考虑相变过程的影响。
目前混合流体模型中采用的空化模型主要分为以下三种,分别为
(1)基于空泡动力学的空化模型[25-30];
(2)基于气液平衡界面理论的空化模型[31];
(3)基于蒸发-凝结相变理论的空化模型[32]。
在这三类空化模型中,基于空泡动力学的全空化模型(full cavitation model)使用最为广泛,发展较为充分。基于蒸发-凝结相变理论的空化模型则从平面界面的蒸发/凝结相变模型出发进行了推导,包含了空化过程中非平衡相变的因素,对翼型绕流等界面曲率不大的空化流场模拟效果较好[33]。
考虑到水泵水轮机中的空化流动复杂,空化形态、发展程度多样,尤其在涡空化流动结构中,选用适宜的空化模型对高水头水泵水轮机空化非定常流动进行预测十分重要。尤其是高水头机组水的弱可压缩性已经体现,充分考虑水的弱可压缩特性是解决高水头机组模拟不准的关键要素。
因此,本文对水泵水轮机稳定性采用考虑水的可压缩性的精确流场捕捉为基础进行高水头水泵水轮机机组内部关键部位复杂流态产生的压力脉动及其所导致的机组振动为研究对象,研究不同工况参数对水泵水轮机的水力性能及运行稳定性机理的影响,采用优化设计方法解决水泵水轮机因水头大变幅带来的振动超标等关键技术难题。
2 梅州抽水蓄能电站概况
梅州抽水蓄能电站位于广东省梅州市五华县南部的龙村镇黄狮村境内,电站建成后,主要服务于广东电网,在电网中承担调峰、填谷、紧急事故备用任务,兼有调频、调相和黑启动任务。
电站规划装机容量2400MW,分两期建设,其中一期装机容量1200MW,安装4台单机容量为300MW,额定转速375r/min的单级立轴单转速混流可逆式机组。电站上水库正常蓄水位815.5m,下水库正常蓄水位413.5m,调节性能为周调节(14h)。
梅州抽水蓄能电站是中国400m水头段的典型代表,其水头变幅达到了1.21,如图2和表1所示,超过了国内两座标杆电站(清远和洪屏)的水头变幅。对于定速抽水蓄能机组而言,水头变幅是影响机组稳定性最重要的因素,变幅越大,其水力优化的难度越大。
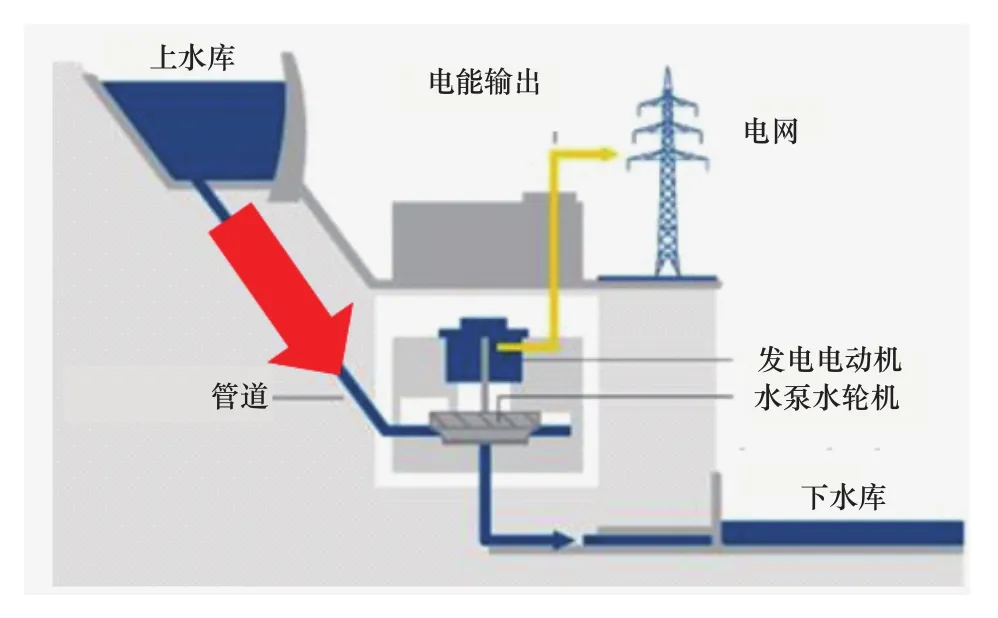
图2 梅州抽水蓄能电站示意图Figure 2 Schematic diagram of Meizhou pumped storage power station
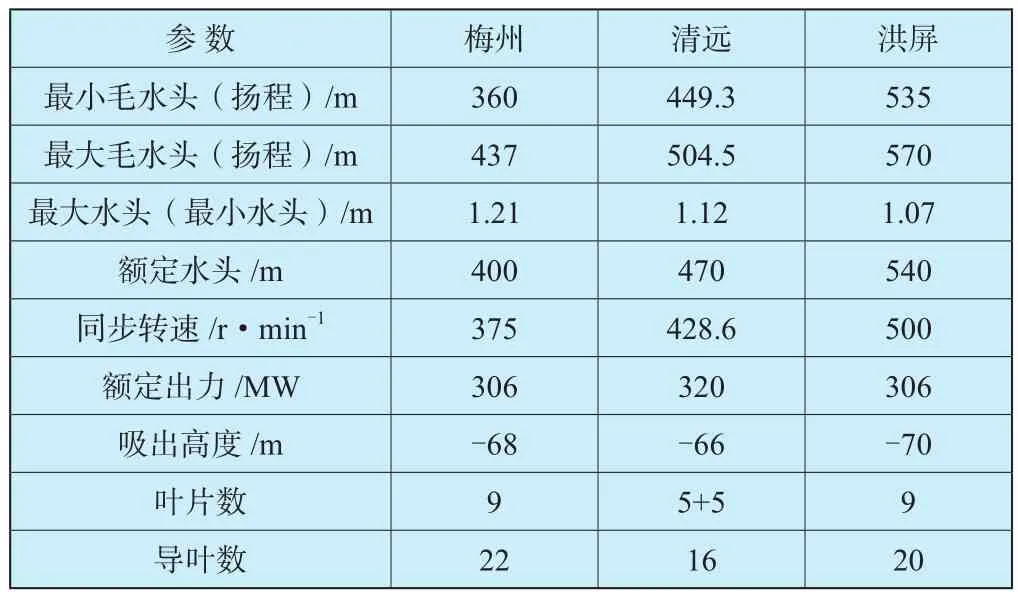
表1 梅州抽蓄电站基本参数Table 1 Basic Parameters of Meizhou Pumped storage
3 弱可压缩流动
对高水头水泵水轮机而言,其弱可压缩性表现突出,尤其是在压力脉动的相似性上,模型机组测试的压力脉动和真机状态的压力脉动极不相似。由于水轮机设计首要考虑的损失最小,所以机组设计时优先考虑的雷诺数相似,对机组安全稳定性有重要影响是压力脉动,而流体湍流和马赫数密切相关。
马赫数是讨论可压缩流体运动的一个重要的无量纲相似准数。在流体密度不变的不可压缩流体中,声速c=∞,Ma=0。从马赫数等于0.1起,流体表现为弱可压缩特性。在可压缩流中,流速相对变化dv/v同密度相对变化之间的关系是dp/p=-Ma2dv/v,即在流动过程中,马赫数越大,气体表现出的可压缩性就越大。
在高水头(H>400m)水泵水轮机实际运行工况,转轮的线速度已经接近100m/s,其马赫数超过0.1,流体的可压缩性已经表现出来。压力波在流体中的传播已经和不可压缩流体表现完全不同。
所谓弱可压缩流动(weakly compressible flow)是指马赫数在0.001<Ma<1之间的流动。声波在水体中传播速度较快(a=1000m/s),而水体本身的流速比声速低得多,在高水头水泵水轮机中大多数工况下水的流速超过100m/s,因此水是一种弱可压缩流体。在实际工程中如水击及绕流产生的旋涡等不稳定流动过程,都要考虑水的压缩性。
尤其当水泵水轮机中局部压力小于空化初生压力而发生空化时,低压区产生大量的气泡,受主流的影响,气泡随着流动流向下游,在高压区碰撞、收缩、溃灭。这一过程中,气泡的密度是可变的,但是通常的计算中这一密度视为常数,这与实际流动有很大的区别[34]。
由状态力程可得流体压力p=(ρ,T),对正压流体即密度只是压力的函数,水中声音的传播速度为:


4 数值计算及分析
4.1 计算模型
为了改善机组的稳定性,确保梅州抽水蓄能水泵水轮机的稳定性,其关键指标压力脉动必须高度重视。以梅州水泵水轮机为研究对象,其设计水头Hr=400m,额定转速n=375r/min,设计工况导叶开度α=24°。水泵水轮机转轮叶片数为9,活动导叶数和固定导叶数均为22,转轮低压侧直径为D2=2.373m。整体计算域包括蜗壳、固定导叶、活动导叶、转轮和尾水管等主流流道,如图3所示。

图3 水泵水轮机流道计算模型Figure 3 Calculation model of pump turbine
计算过程中的边界条件和相关参数设置如下。在蜗壳进口断面设置质量流量边界,在尾水管出口断面设置压力出口边界。为了合理地计算动静干涉强度,采用了mesh motion方法设置转轮内部网格的旋转。计算过程中使用V2F模型对瞬态RANS方程进行求解。时间步长取10-3s,共计算转轮旋转35个周期。
其中各区域Y+值的分布云图展示于图4。为了尽可能精确地模拟压力脉动,对各计算域均采用了较为稠密的网格划分,使得总体计算网格数达到997万。观察可知各计算域中大部分区域的Y+处于合理范围内,这也是合理计算的前提。
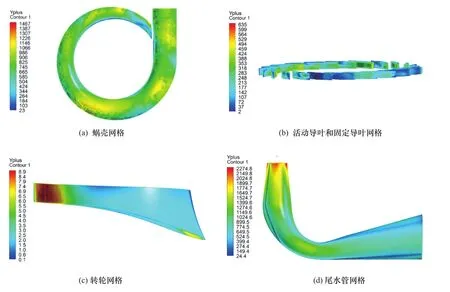
图4 水泵水轮机各计算域Y+值分布Figure 4 Y+ value distribution in each calculation domain of pump turbine
选取设计工况开展压力脉动特性的计算。为了验证考虑可压缩性模拟的精度,以真机试验结果为参照,将考虑弱可压缩性和不考虑可压缩性所模拟的无叶区压力脉动幅值对比展示于图5。其中,考虑可压缩性模拟在波速a=1200m/s的条件下进行。观察可知,在不考虑可压缩性时,无叶区压力脉动的频域分布较为合理,但幅值显著低于真机试验结果。当考虑可压缩性后,无叶区压力脉动幅值与真机试验结果的差距被显著缩小。在频域构成中,考虑可压缩性显著提高了两倍叶频的幅值,而其他阶次的叶频幅值并未发生显著变化。
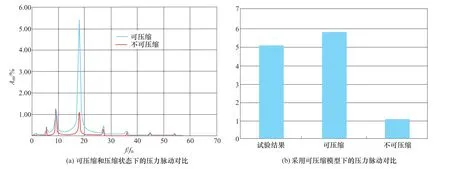
图5 考虑可压缩性所模拟的无叶区压力脉动幅值强度与不可压缩结果及真机试验结果对比Figure 5 Comparison of simulated pressure fluctuation amplitude intensity in vaneless region with incompressible results and considering compressibility of protype test results
为了研究压力脉动传播过程中的衰减规律,在无叶区转轮上游侧设置7个压力监测点,如图6所示。这些压力脉动测点在径向分布上位于转轮叶片的前缘与活动导叶的尾翼之间,能够全面呈现无叶区压力脉动的分布特征。
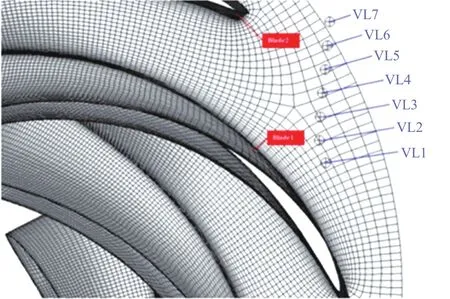
图6 无叶区转轮上游侧压力脉动监测点分布Figure 6 Pressure fluctuation monitoring points on the upstream side of the runner in the leafless area
4.2 几何参数对压力脉动的影响
水泵水轮机压力脉动是水流受旋转部件和静止部件共同作用而产生。这意味着,旋转部件(转轮)或静止部件(导叶、蜗壳和尾水管)的几何参数对压力脉动强度均存在影响。从水泵水轮机固有属性出发,研究其对压力脉动的影响,对于提高水力发电设备的可靠性具有重要意义。作者尝试从多个方面研究几何参数对压力脉动特征的影响,包括对叶片头部缩进、修改蜗壳断面面积分布、调整固定导叶数量、改变尾水管形状等措施。初始几何参数的定义为AAAA,将蜗壳区域定义为第一个A,导叶区域定义为第二个A,转轮区域定义为第三个A,尾水管区域定义为第四个A。限于篇幅的原因,本文仅从叶片头部缩进和导叶形状对压力脉动的影响,也就是第二个A和第三个A进行改变,研究其改变对机组性能的影响。
4.2.1 转轮修型
对于动静干涉影响最为核心的部件是转轮,对比了几种转轮形式对压力脉动的影响,如图7所示。对于转轮而言,其进口边(LE)和出口边(TE)的形状、位置、曲率变化、厚度均对压力脉动产生影响,如图7所示。

图7 流道结构形式Figure 7 Flow passage structure
对于原转轮A进行了四种改型,分别为转轮B(出口边凹进3cm),转轮C(出口边凹进5cm),转轮D(出口边前倾6°)和转轮E(出口边后仰6°),如图8所示。

图8 不同转轮结构形式对比Figure 8 Comparison of different runner structures
分别研究A,B,C,D和E五种方案其对压力脉动的影响,通过改变转轮翼形的办法降低无叶区压力脉动,随着动静干涉的减弱(A-B-C)无叶区压力脉动可以得到明显降低,如图9所示。

图9 不同转轮叶片形状对不同部位压力脉动的影响Figure 9 Influence of different runner blade shapes on pressure pulsation at different parts
当对于高水头水泵水轮机,由于无叶区空间狭窄,脉动能量的衰减有限,可能致使脉动能量窝在无叶区空间内,使得动静干涉引起的压力波提前出现波的传播与叠加,并增加转轮圆周压力波的幅值分布的不均匀性,这时候配以转轮叶片头部适当修型可以改善转轮进口压力波的圆周分布均匀性。如图10(a)所示,通过某一测点对比转轮方案C与A相比,根据计算结果对比,可以发现对压力脉动的改善,其改善幅度为50%。
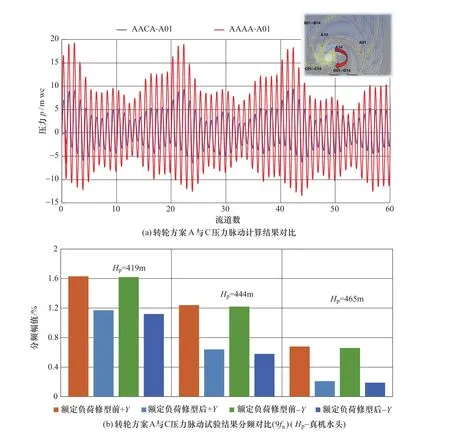
图10 不同转轮叶片形状对某一测点压力脉动的影响Figure 10 Influence of different runner blade shapes on pressure fluctuation at a measuring point
图10(b)根据试验结果的对比情况,可以发现在机组在额定负荷,+Y和-Y压力脉动测点的9fn分频幅值改善了50%。
4.2.2 导叶影响
为了分析固定导叶对压力脉动的影响,共设计了四种导叶形式,如图11所示。其中,导叶A数目为20,作为基础参照设计。导叶B和C数目为19,其中固定导叶C厚度较固定导叶B更薄。固定导叶D数目增加至22,且与固定导叶C厚度均匀减薄。以固定导叶A与固定导叶B为例,展示了蜗壳与双列叶栅的网格拓扑结构,如图12所示。为了准确地模拟压力脉动幅值,在双列叶栅附近使用了稠密的网格分布。

图11 四种固定导叶形状Figure 11 Four fixed guide vane shapes
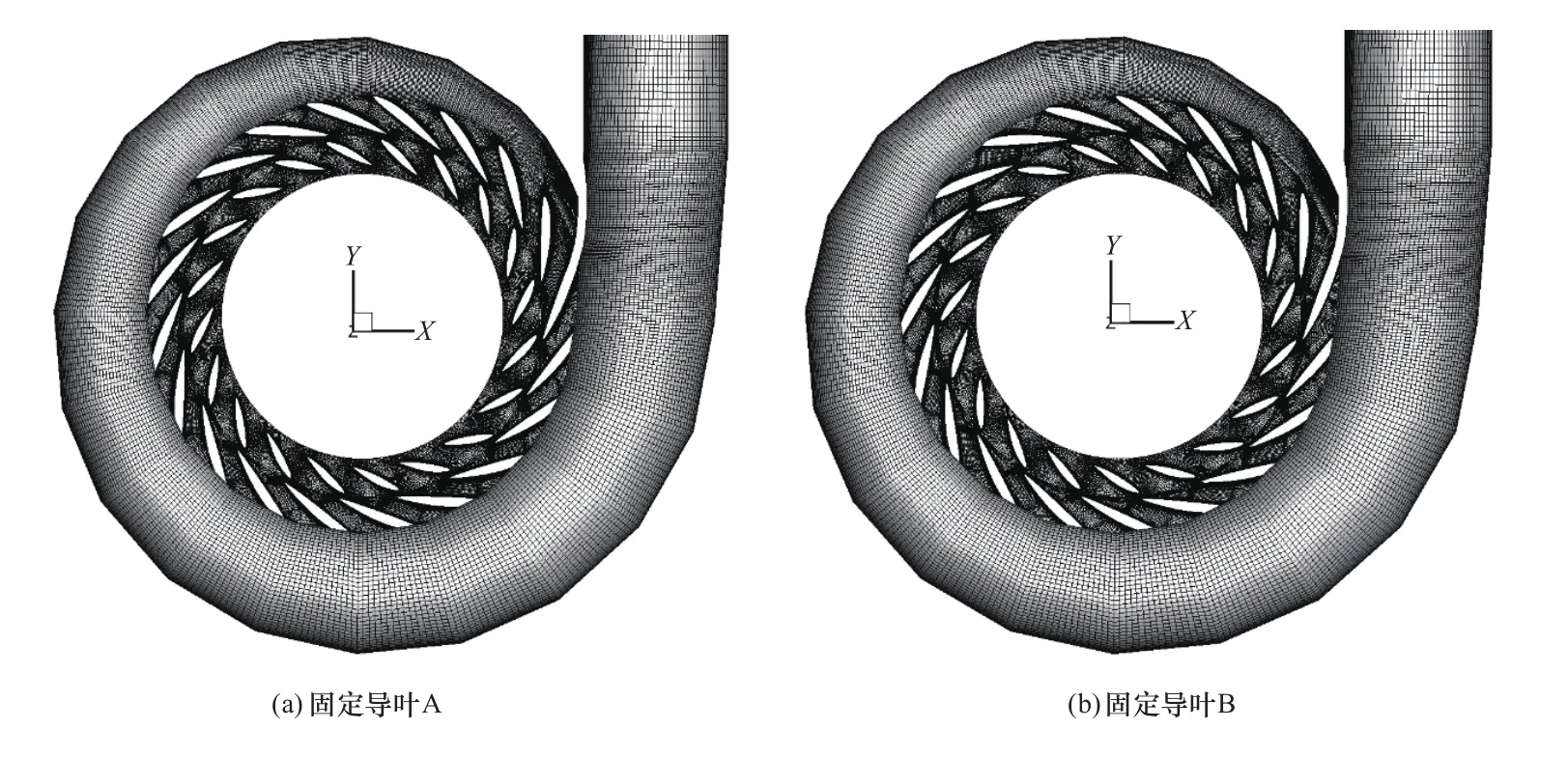
图12 固定导叶A与固定导叶B网格划分Figure 12 Grid division of fixed guide vane A and fixed guide vane B
图13展示了四种固定导叶布置下蜗壳内部压力脉动幅值分布图,包含计算模型中一阶、二阶、三阶叶片转动频率。首先,当采用不同的固定导叶数时,压力脉动发生频率会有所改变。其次,各固定导叶不同阶次幅值的分布规律有所差异。其中对于一阶叶频,固定导叶A的幅值在蜗壳末端幅值较高,但随着测点逐渐接近蜗壳进口断面,其幅值衰减速度较快。固定导叶B、固定导叶C的一阶叶频幅值分布较为相似,而固定导叶B的幅值水平增加。固定导叶D的幅值分布与前者有所区别,其在蜗壳末端幅值较低,而随着测点靠近蜗壳进口断面逐渐升高。对于二阶叶频,固定导叶D的幅值显著低于固定导叶A、固定导叶B、固定导叶C,且在蜗壳内部具有较快的衰减速度。因此,在四种固定导叶布置中,固定导叶D对于压力脉动的衰减具有较好的效果。
图14展示了固定导叶A、B、D布置下转轮进口至蜗壳段压力脉动幅值分布图。观察可知,在每一种固定导叶布置下,压力脉动传播过程中幅值衰减速度随着叶频阶数增加而加快,而一阶叶频的衰减速度最慢。此外,在固定导叶D布置下,压力脉动叶频幅值整体水平较其他布置略低。这说明,应用固定导叶D布置可以实现更低的压力脉动水平以及更快的传播衰减。
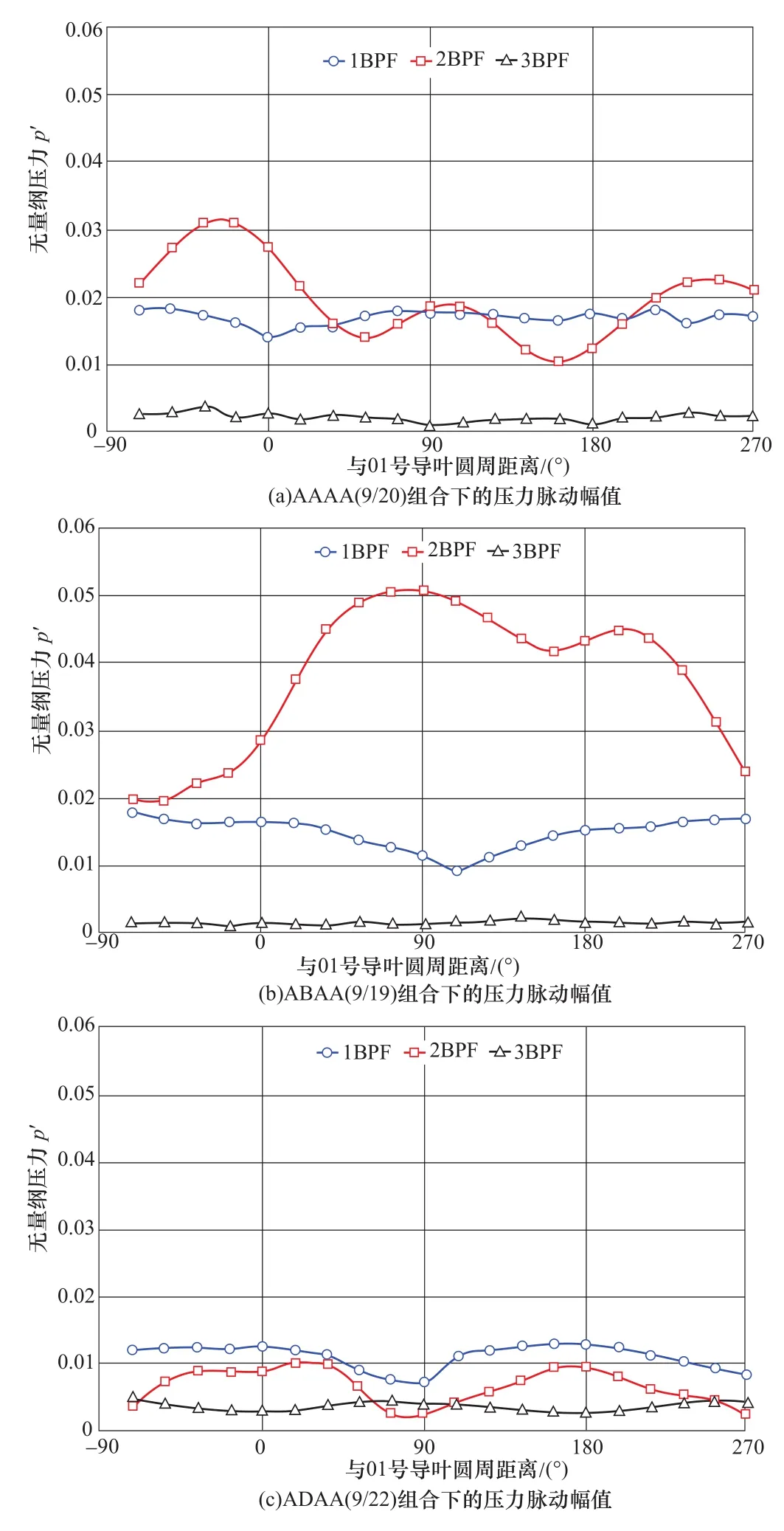
图14 固定导叶A、B、D布置下导水机构内压力脉动幅值分布图(1BPF —一倍叶片数通过频率;2BPF —二倍叶片数通过频率;3BPF —三倍叶片数通过频率)Figure 14 Distribution diagram of pressure fluctuation amplitude in the water guide mechanism under the arrangement of fixed guide vanes a,B and D
图15展示了固定导叶D布置下一阶、二阶、三阶叶频的相位分布图。其中,二阶叶频的相位分布较为规律,且在传播过程中保持了周期性。与此相比,一阶、三阶叶频在蜗壳内部的分布情况则相对不规律。9和22组合下的相位角呈现周期性。
根据研究分析,动静干涉产生的压力波在向蜗壳传播的过程中,如果相位相同,将会发生波的叠加,将会放大压力脉动幅值。如图16所示,对于转速428.6r/min的机组而言,其18倍叶片通过频率的标准波长为9.3m。压力波在一个周期内传播的距离为9.78m,多个压力波在该时刻到达相同的位置附近,就发生了压力波的叠加。

图16 压力波叠加现象的理解Figure 16 Explanation of pressure wave superposition phenomenon
4.3 研制结果
梅州抽水蓄能电站是南方电网公司的重点项目,是确保大湾区安全用电的一把利器。梅州抽水蓄能机组的水力研发呈现几个特点:开发周期短,设计难度大。为了确保梅州抽水蓄能2022年按时发电,与其他项目相比,梅州抽水蓄能机组水力开发周期比较短。设计难度主要体现:首先是变幅大,梅州抽水蓄能电站最大水头与最小水头比值达1.21,水头变幅处于国内外抽水蓄能电站前列;其二是机组吸出高度相比同水头段机组偏低,带给机组的水力开发难度剧增。采用上述可压缩计算,消除不稳定漩涡于细微之间,优化转轮和导叶翼型,实现了动静干涉的最优匹配。
机组投运后是国内抽水蓄能机组中,水轮机工况和水泵工况国内首座机组的上导、下导和水导的振摆为0.05mm,机组的稳定性非常突出,如图17所示。
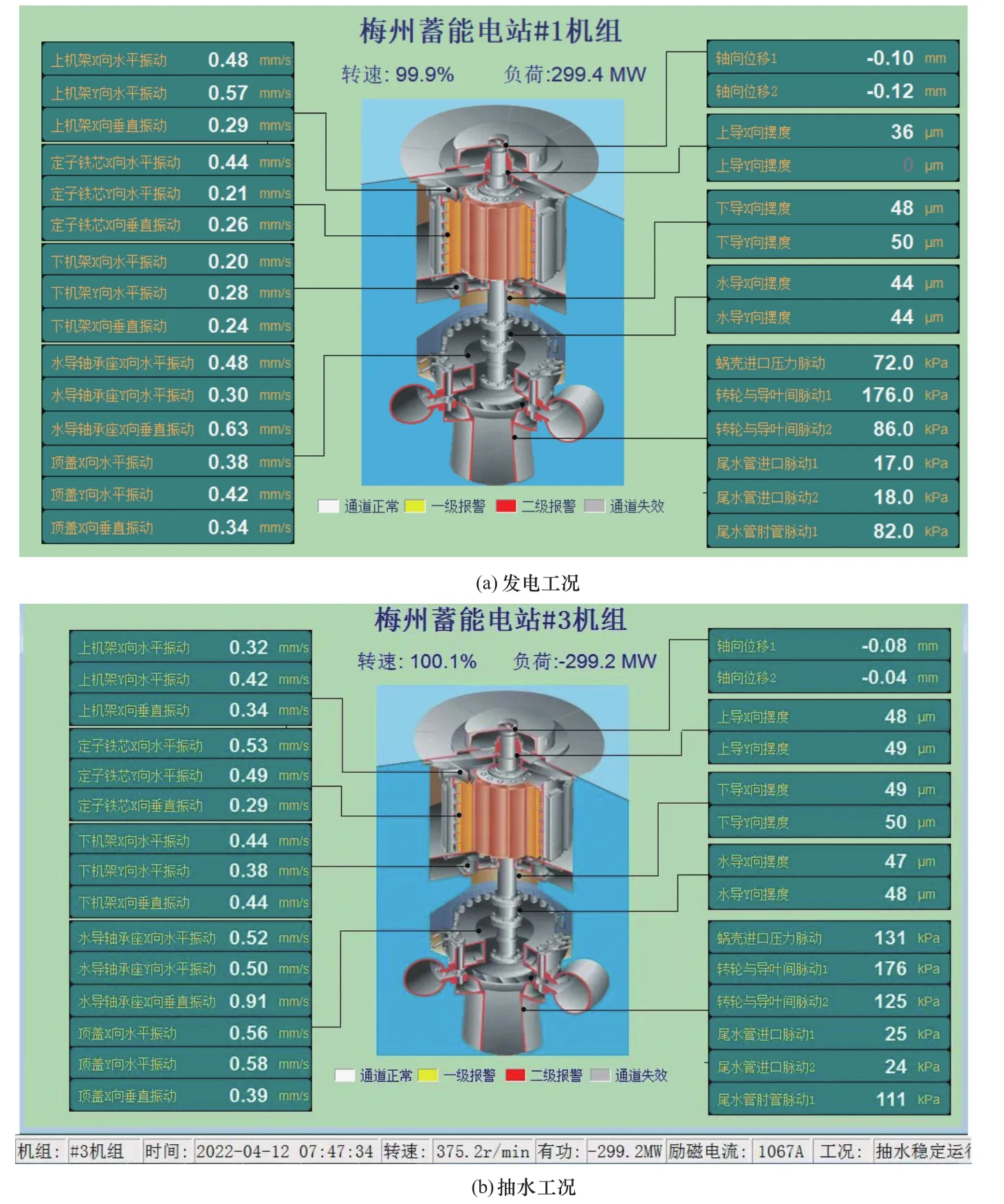
图17 梅州抽水蓄能电站运行振摆情况Figure 17 Operation vibration of Meizhou pumped storage power station
5 结语
正是以弱可压缩计算和V2F湍流模型为基础,对水泵水轮机内的流动进行了精细模拟,将诱发不稳定的漩涡分离采用新型转轮和导叶组合模式和特殊的翼型设计进行抑制,从而实现了水头大变幅的抽水蓄能机组稳定运行。实现了梅州机组以其优秀的稳定性成为400m抽水蓄能机组的标杆之作,并且是产学研用的一个优秀案例。
6 致谢
感谢在项目研究和论文撰写过程中,得到了很多行业专家的大力支持,如中国水利水电科学研究院的孟晓超教授级高级工程师,东方电气风电股份有限公司的贺建华教授级高级工程师,南方电网调峰、调频发电公司的刘国刚教授级高级工程师,在此一并感谢。
