改进的灰狼优化算法在SVM参数优化中的应用

宋玉生， 刘光宇, 朱 凌， 王 坚

(1.杭州电子科技大学 自动化学院，浙江 杭州 310018；2.浙江财经大学 信息管理与人工智能学院，浙江 杭州 310018)

0 引 言

支持向量机(support vector machine,SVM)是一种专门针对小样本而提出的有监督机器学习方法，该方法具有结构简单、泛化能力强和易于实现等优点。目前,SVM已经广泛应用于机器学习的各种领域，如人脸图像识别[1]、语音情感识别[2]及故障诊断[3]等。SVM的性能受模型内部参数影响较大[4]，选择合适的SVM参数可获得较好的SVM分类效果。为此，许多学者提出多种SVM的参数选择方法，如网格搜索、双线性搜索、遗传算法等。其中网格搜索方法非常耗时，而且只能找到给定的格点上的值，有一定局限性。许多学者利用蚁群优化算法[5]、粒子群优化算法[6]等方法对SVM的参数进行寻优，但这些算法在存在易陷入局部最优和求解精度低等问题，无法获得较理想的SVM模型参数。

2014年,Seyedali M等人[7]提出灰狼优化(gray wolf optimization,GWO)算法，该算法具有结构简单、全局性好等优点，更适合SVM的参数寻优。但GWO算法仍然存在易陷入局部最优、开发能力不足等问题。

本文在原GWO基础上使用控制参数非线性递减和随机权重的位置更新策略来改进GWO。在标准的测试函数上进行仿真实验，结果表明,改进的灰狼优化(improved gray wolf optimization,IGWO)算法性能优于GWO。随后将IGWO应用于光伏阵列故障诊断的SVM参数寻优过程中。实验结果表明，IGWO-SVM模型在光伏阵列故障诊断中有很好的表现。

1 SVM

对于非线性近似可分样本的SVM优化问题可描述为[8]

(1)

s.t.yi(ωTφ(xi)+b)≥1-εi,i=1,…,n

(2)

式中ω为超平面法向量，εi(εi≥0)为松弛变量，C为惩罚因子，用来对错误分类进行惩罚。n为训练样本个数，yi∈{+1,-1}为类别标签，φ(·)为低维空间到高维空间的映射函数。

在式(1)和式(2)的基础上引入拉格朗日函数、对偶原理及核函数，获得SVM的决策函数，其具体表达式为

(3)

K(xi,x)=exp{-g‖xi-x‖2}

(4)

式中ai为拉格朗日因子，K(xi,x)为高斯核函数，g为核函数参数。

2 标准GWO算法和IGWO算法

2.1 标准GWO算法

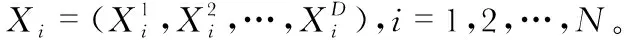
(5)

A=2a·r1-a

(6)

C=2·r2

(7)

a=2-2t/tmax

(8)

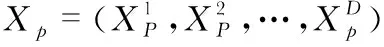
然而,在猎捕过程中猎物的实际位置是未知的，由于α,β,δ狼更接近猎物，将α,β,δ狼的位置近似视为猎物的位置，通过式(5)～式(8)来更新各灰狼的位置，最后对位置求平均得到灰狼ω的最终位置。灰狼位置更新的具体过程如式(9)～式(10)所示

(9)

(10)

式中Xα，Xβ，Xδ分别为本次迭代适应度为前三的灰狼的位置。A1，A2，A3和C1，C2，C3为每次迭代时产生的系数。

2.2 IGWO算法

2.2.1 控制因子非线性递减策略

群体智能算法前期注重算法的全局搜索，后期注重算法的局部开发[9]。较强的全局搜索能力能避免算法的早熟收敛，较强的局部开发能力可提高算法后期的收敛速度。GWO作为群体智能算法的一种，其全局搜索和局部开发能力的协调为算法较快获得全局最优的关键。

在GWO算法中，当A≤1时，灰狼攻击猎物，进行局部搜索，当A>1时，灰狼散去，进行全局搜索。由式(8)可知，参数A随着控制因子a的变化而不断的变化。因此，整个围捕猎物过程主要通过参数a的线性变化来完成。控制参数a在迭代过程中的变化方式影响算法的开发和搜索能力的平衡。标准的GWO算法的参数a是线性递减的，然而,在算法搜索过程并非线性变化的，因此,参数a的线性变化无法适应实际的搜索情况。尤其在解决多峰函数问题时，GWO容易陷入局部最优[7]。为此，本文提出一种非线性控制因子策略

(11)

在迭代初期a的衰减速度较小，式(6)中A的值波动较大，算法更容易跳出局部最优，从而提升了算法的全局搜索能力。迭代后期a的衰减速度较大，算法在局部更快找到最优解。因此,改进的控制策略较好地平衡算法的全局搜索和局开发的能力。

2.2.2 随机权重的位置更新策略

由式(9)和式(10)可知，标准的GWO算法以三个最佳灰狼的位置平均值作为下次迭代的灰狼的位置，该方法并未考虑实际灰狼种群的等级差异。在实际的寻优过程中，起引导作用的α,β,δ狼的适应度依次降低，α狼的位置更可能接近实际最优解。为突出最优狼对种群的全局带领能力，在位置更新过程中增加α狼的位置权重，同时减小δ狼的权重。同时为进一步避免算法的陷入局部最优，在保证α狼权重系数大于δ狼权重系数的情况下，采用随机权重更新下一代种群的方式。本文引入随机权重的位置更新策略

(12)

式中r3为[0,1]之间的随机数。

3 建立IGWO-SVM的分类模型

SVM模型惩罚因子C表示用最优超平面对样本进行分类时对错分的容忍程度，其权衡了SVM分类正确率与模型复杂度的关系[10]。C越大，训练数据集的分类正确率越高，但分类间隔减小，容易出现过拟合问题，分类器对推广泛化能力降低。反之，训练数据集被错分的几率增大，分类间隔增大，但容易出现欠拟合问题，分类器的泛化能力也会降低。

高斯核函数中g确定原始数据特征空间和高维数据特征空间的映射关系[11]。g较大时，高斯核函数的数值将趋近于0，SVM会对所有的训练样本正确分类，但分类超平面会变复杂，模型的泛化能力降低。g较小时，SVM判别函数将趋近于1，模型会把所有的测试样本判断为训练样本较多的一类，模型的推广能力依旧不好。找到合适的惩罚因子C和核函数σ对SVM在样本的泛化能力推广有重要意义。本文利用改进的GWO算法对SVM参数进行优化。

IGWO优化SVM参数的流程如下：

1)输入实验数据，为消除量纲对分类的影响，对原始数据集进行归一化处理，具体处理方式如下

(13)

式中x为原始的数据特征；xmin和xmax分别为每组特征的最小值和最大值，y为归一化处理后得到的数据。

2)将整个数据集按着比例随机分成训练集和验证集两部分，其中训练集用于训练SVM模型，验证集用来对SVM模型评价和选择。

3)将灰狼将参数C和参数g作为灰狼的位置参数，对灰狼的种群规模、个体维度、参数寻优范围和算法最大迭代次数进行初始化。

4)利用参数C和参数g在训练集上得到SVM模型，将得到的模型在验证集上进行分类，将分类正确率作为每匹狼的适应度值。

5)根据适应度值将灰狼种群划分为α，β，γ和ω共4个等级。

6)根据式(5)～式(7)、式(9)、式(11)和式(12)对种群中每个灰狼位置进行更新。

7)判断是否达到最大迭代次数，若达到则参数寻优结束，否则转向步骤(4)，利用灰狼更新后的位置参数继续进行迭代寻优。

8)迭代结束时输出最优狼位置，即C和g的值，并且利用C和g建立SVM分类模型。

4 算例结果与分析

4.1 利用标准数据集对IGWO进行性能分析

为测试IGWO算法的寻优能力，使用IGWO算法和标准的GWO算法在10个标准测函数上进行仿真实验，统计并分析两种算法在不同测度下的仿真结果如表1。仿真函数分别为Sphere (f1),Sum of Different Powers (f2),Schwefel1.2(f3),Schwefel2.21(f4),Rosenbrock(f5),Step(f6),Quartic Function with noise(f7),Schwefel 2.26(f8),Rastrigin(f9),Penalized(f10),其中，f1-f5为单峰函数，f6-f10为多峰函数。10个测试函数的维度设置为30，测试函数的理论最优值都为0。算法的参数设置：种群规模N=30，最大迭代次数tmax=500。

表1 IGWO和GWO对10个测试函数的寻优结果

利用IGWO和GWO分别进行30次迭代实验，用30次实验结果的最优值(Best)、最差值(Worst)和平均值(Mean)评价算法的寻优精度，用30次实验结果的标准差(St.dev)来评价算法的稳定性。

由表1的实验结果可知，IGWO在单峰和多峰测试函数上表现都优于GWO。相比GWO,IGWO得到的均值、最优值和最差值更接近理论最优值，说明改进策略提升IGWO的寻优精度。同时IGWO获得的结果的标准差更小，说明改进算法的稳定性更高。IGWO在函数f7,f8和f9上获了全局最优的结果，而GWO只在函数f7上获得理论最优值，表明改进策略有效提升GWO算法克服陷入局部最优的能力。

为更直观反映IGWO在参数寻优方面的优势，图1给出IGWO算法和GWO算法在3个标准测试函数f1,f3和f6寻优收敛曲线。从图1可清晰地看出，IGWO较快的收敛速度和收敛精度。

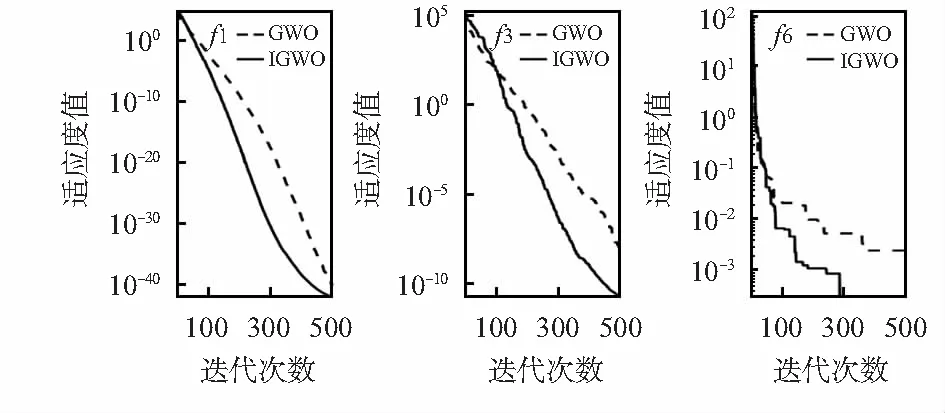
图1 IGWO和GWO在函数f1,f3,f6上的寻优迭代曲线

4.2 IGWO-SVM算法在光伏故障诊断的应用

本次实验数据来源于本团队自主研发的微型光伏电站系统。该系统利用传感器采集光伏阵列的工作状态信息，包括系统内部的电流、电压等电气信息和系统工作的温度、光照强度等环境信息。系统包含8块光伏组件，在采集实验数据时，设置4种常见的光伏故障类型来模拟实际的光伏故障，其中包括断路、短路、全部遮挡和部分遮挡，同时设置正常的工作状态作为一种特殊的故障类型。各种故障的具体的实现方式如表2所示。

表2 光伏阵列故障状态类型

采用微型光伏电站系统在中国浙江某地的2020年8月14日上午9：00～下午3：00的室外环境下的6908组实验数据。本次实验在一个微电站上进行实验，每隔一定时间切换一种故障状态，分别记录不同故障状态下的故障样本数据。每个样本包含输出电压、总输出电流、外界光照强度和外界温度4个特征值。整个实验过程光照强度和光伏整列输出随时间变化曲线如图2所示。

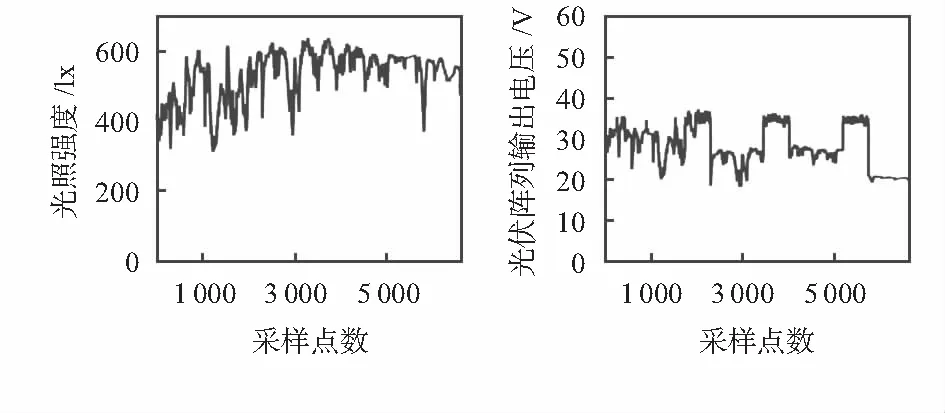
图2 光照强度和光伏整列输出随时间变化曲线

本次实验采用简单的交叉验证方法，将整个实验数据分为训练集和验证集，测试集和验证集各占总数据量的70 %和30 %。用验证集的分类正确率作为优化算法的适应度，利用训练集对SVM模型进行训练。同时将灰狼种群设置为10，最大迭代次数设置为30。此参数寻优的范围设置为C∈[0.1,100],g∈[0.1,100]。在MATLAB平台上利用LIBSVM[12]进行实验。

IGWO-SVM和GWO-SVM在整个迭代过程中适应度变化如图3所示。由图可知，IGWO-SVM在第6代左右即达到最大的适应度值，而GWO-SVM在第10代左右才达到其最大的适应度值。IGWO-SVM比GWO-SVM更快达到更大的适应度值，说明IGWO-SVM在真实的光伏故障数据集上有更快的收敛速度。同时IGWO-SVM模型的最大适应度值大于GWO-SVM的最大适应度值，说明IGWO-SVM有更高的收敛精度，同时IGWO-SVM模型在一定程度上克服了GWO-SVM陷入局部最优的问题。

图3 寻找最佳参数适应度曲线

IGWO算法在获得最大适应度时对应的C为13.7,g为0.34，同时GWO算法在获得最大适应度时对应的C为2.1,g为1.3。利用所得的参数在训练集上建立SVM分类器模型进行训练，之后利用该模型对光伏阵列故障验证集进行分类。

由表3可知，IGWO-SVM模型相比GWO-SVM模型在C3,C4三种故障类型的识别正确率均有提升，尤其对C4故障判断的准确率提升幅度较大。短路故障(C4)是微电站系统中非常严重的故障，该故障容易引起微电站系统性故障，对系统安全平稳运行极为不利。本文提出的IGWO-SVM模型极大地提升了短路故障的识别率，对光伏阵列的故障诊断有很高的实用价值。

表3 光伏阵列故障分类的实验结果

5 结 论

本文针对SVM参数C和参数g的选择困难问题，提出一种IGWO优化SVM参数的方法。在GWO算法的基础上，引入非线性控制因子和新的位置更新策略，利用标准测试函数对GWO算法性能进行验证，结果表明:改进策略提高算法的全局搜索能力和局部开发的能力。随后建立IGWO-SVM模型，利用IGWO对SVM的参数进行优化，并将该模型应用到光伏阵列故障诊断。最后实验验证了IGWO-SVM模型的优越性。