基于改进PSF参数估计的仪表模糊图像复原与识别*
2022-09-08孙绍祖刘今越史宝军
孙绍祖, 刘今越, 史宝军
(河北工业大学 机械工程学院,天津 300401)
0 引 言
石化爆燃环境中存在有大量的气压表、温度表、油温表等指针式仪表[1],传统的仪表检测靠人工进行识别,危化品生产储运场仪表数量多、环境复杂,人工识别工作量大、成本高、易发生误读误记,存在较大安全隐患。近年来,随着机器人智能化水平的不断提高,大量智能机器人被应用于变电站、煤矿、石化爆燃环境下的巡检作业[2~4],进行指针式仪表识别,许多学者对此进行了大量研究。文献[5]提出基于双目立体视觉的指针式仪表判读算法,用于校正指针式仪表中指针针尖在图像上的位置。文献[6]提出一种基于直线椭圆检测器的指针仪表自动识别策略,对刻度不均匀的指针式仪表识别有很好的启发作用。文献[7]引入一种二进制描述器进行指针区域获取,之后基于圆的区域累积直方图(circle-based regional cumulative histogram,CRH)精确提取指针。目前,仪表识别方面的研究,多是基于相机固定的情况下对获取的仪表图像进行识别检测,而在石化爆燃等高危复杂环境下,机器人运动或不可避免的振动,都会导致拍摄目标与相机的相对位移,从而产生图像运动模糊退化,对读数识别产生很大干扰。
本文提出基于图像分块结合边缘检测的模糊参数估计方法,并通过实验验证了提出方法对模糊参数估计的准确性。基于估计出的点扩散函数(point spread function,PSF),采用维纳滤波完成运动模糊仪表图像复原,对复原图像再处理后,通过Hough变换完成仪表识别。
1 运动模糊图像复原
1.1 运动模糊图像退化模型
对模糊图像[8]进行复原的关键是建立图像的退化模型,在考虑噪声的情况下,图像的退化模型可近似用统一的线性模型表示为
g(x,y)=f(x,y)*h(x,y)+n(x,y)
(1)
式中g(x,y)为退化图像;h(x,y)为退化函数;f(x,y)为原始图像;n(x,y)为随机噪声函数;*为卷积。
对式(1)进行傅里叶变换则有
G(u,v)=F(u,v)H(u,v)+N(u,v)
(2)
式中G(u,v),F(u,v),H(u,v),N(u,v)分别为式(1)各函数的傅里叶形式。原图像f(x,y)通过退化函数PSF影响退化后的图像为g(x,y),求解PSF是复原模糊图像的核心问题。
由于变速与非直线运动时都可分解为各段的匀速直线运动,所以,研究匀速直线运动产生的运动模糊具有普遍意义[9],PSF由下式表示

(3)
式中θ为物体运动方向与水平方向之间的夹角,称为运动模糊角度,L为运动方向上像素移动的距离,称为运动模糊尺度。得知模糊角度θ与模糊尺度L,便可求解PSF,进而进行运动模糊图像复原。
1.2 图像预处理
1.2.1 图像灰度化
图像的阈值分割、特征提取等都是以图像的灰度值作为输入量进行计算的[10]。本文通过加权平均法对图像进行灰度处理,如式(4)所示
g=0.229R+0.587G+0.114B
(4)
式中g为灰度值,R为红色光谱分量,G为绿色光谱分量,B为蓝色光谱分量。
1.2.2 图像去噪
本文实验采用高斯噪声进行模拟,由于高斯滤波对处理高斯噪声十分有效,且去除噪声的同时能保留图像原有的特征,因此本文选择高斯滤波进行图像去噪。图1(a)是对模糊仪表图像添加均值为0,方差为0.002的高斯噪声的运动模糊仪表图像,利用5×5的模板进行高斯滤波后的图像如图1(b)所示。

图1 高斯滤波效果
1.3 运动模糊参数估计
1.3.1 边缘检测与图像分块
运动模糊图像中有很多区域是单一色调,灰度值差异不大,受退化函数影响后造成的像素叠加在视觉上并不明显,对全局图像进行模糊参数估计时,造成估计结果不准确。本文提出改进的PSF参数估计方法,在参数估计之前,对图像运用Canny[11,12]算法进行边缘检测,之后进行图像分块,筛选出边缘信息较多的图像块,选择这些图像块的原因是其边缘处灰度值变换剧烈,像素叠加后模糊效果明显,对这些区域进行模糊参数估计结果更加准确。对图1(b)进行边缘检测与图像分块后如图2所示。

图2 边缘检测与图像分块
1.3.2 运动模糊图像的倒频谱分析
本文首先将退化图像进行二维傅里叶变换,之后取对数,再进行逆傅里叶变换得到退化图像的倒频谱,分离出退化图像的模糊信息。
图像g(x,y)的倒频谱定义如下
Gg(p,q)=F-1{log|G(u,v)|}
(5)
式中F-1为傅里叶逆变换,Gg(p,q)为运动模糊图像的倒频谱。在实际的图像处理中,图像的倒频谱一般表示为
Gg(p,q)=F-1{[1+log|G(u,v)|]}
(6)
在不考虑噪声的情况下,式(1)的倒频谱可表示为
Gg(p,q)=Gf(p,q)+Gh(p,q)
(7)
式中Gf(p,q)为原始图像倒频谱,Gh(p,q)为退化函数倒频谱。由式(7)可看出,空间域的卷积运算在倒谱域转变为加法运算,有利于分离模糊图像的模糊信息。图3(a)与图3(b)分别为运动模糊图像图1(b)的频谱图与倒频谱图。

图3 运动模糊图像频谱图与倒频谱图
图3(a)与图3(b)对比可以看出,图1(b)频谱图中心出现十分明显的十字亮线,原因是频谱图中心化过程中图像边缘存在一定的截断,破坏了周边的卷积关系,使退化过程不是一个完全卷积。倒频谱可有效减弱十字亮线的干扰,倒频谱中条纹的方向就是运动模糊图像的运动模糊角度。
1.3.3 运动模糊角度估计
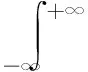
Radon变换是指图像在某一指定角度射线方向上投影的变换,通过Radon变换可以计算图像在任意方向上的投影[13]。函数f(x,y)沿任意角度θ的Radon变换定义为
(8)
其中
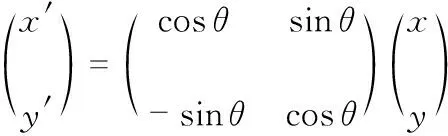
(9)
首先采用Canny算法对图像倒频谱进行边缘检测,图4是对图3(b)运动模糊图像倒频谱图进行Canny边缘检测的结果。对Canny边缘检测后的倒频谱图进行1~180 °的Radon变换, 得到180列矩阵,矩阵中各列的值表示图像在某个方向上沿一族直线积分所得的投影值。通过找到矩阵中的最大值所在的列,便可得到运动模糊角度。

图4 倒频谱Canny边缘检测
1.3.4 运动模糊尺度估计
在求解出运动模糊角度的基础上,首先根据模糊角度将模糊图像旋转到水平方向后,再根据倒频谱低幅值体现的模糊图像特性,计算出对称两个负峰值之间的距离,负峰值间距离的1/2即为运动模糊尺度。设第一个负峰值点Cg(p1,q1)和第二个负峰值点Cg(p2,q2),则两个负峰值之间的距离为
(10)
图像的运动模糊尺度为
(11)
1.3.5 模糊参数估计实验
选取分辨率为340×340的指针式仪表图像,人工添加模糊角度与模糊长度以及均值为0,方差为0.002的高斯噪声,分别用频谱法与本文算法进行模糊参数估计,通过与真实值对比,验证算法的有效性。模糊角度与模糊尺度估计的实验结果分别如表1和表2所示,两种算法的误差效果比较如表3所示。
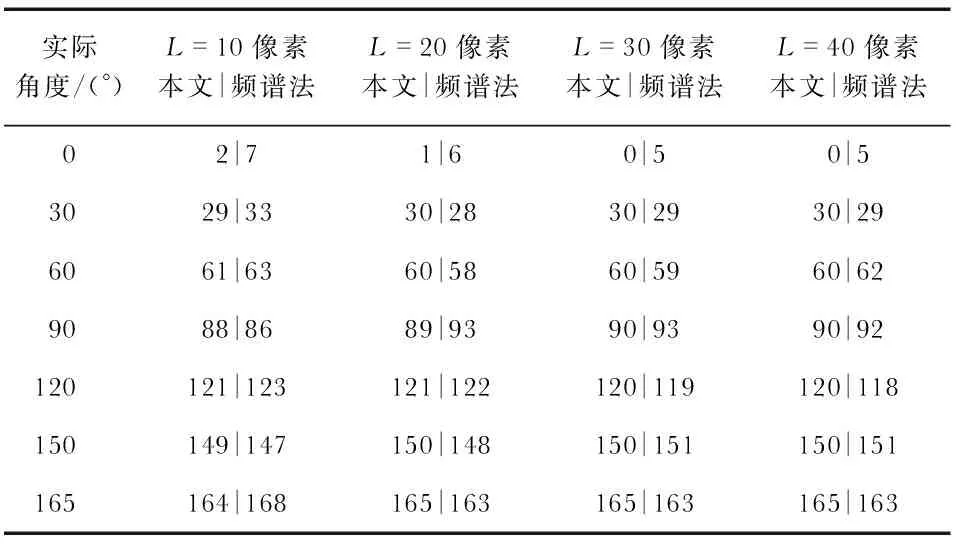
表1 模糊角度估计
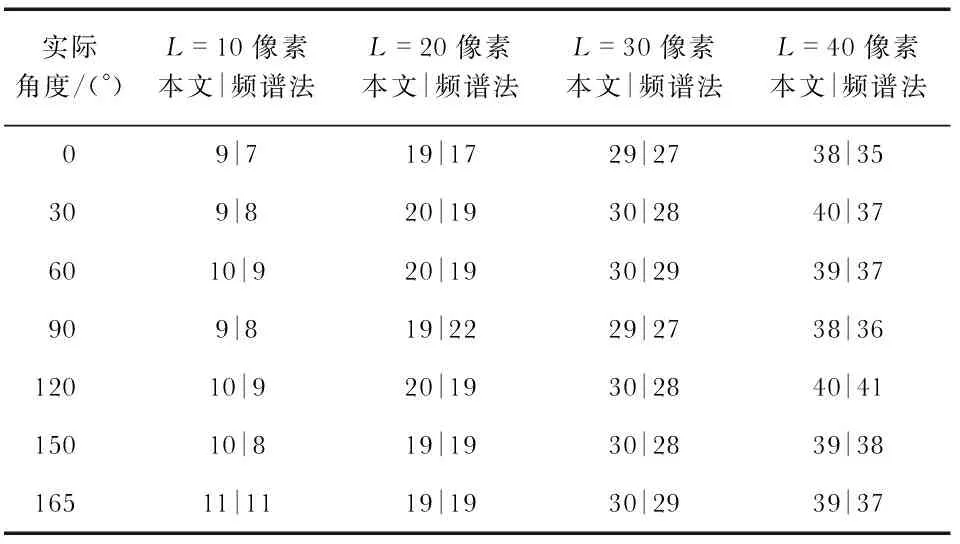
表2 模糊尺度估计

表3 两种算法效果比较
从实验结果可以看出,本文算法估计的运动模糊角度平均误差为0.46°,估计运动模糊尺度平均误差为0.61像素,运动模糊角度估计误差在2°以下,模糊尺度估计误差在2像素以内,具有更高的模糊参数估计精度与稳定性。
1.4 运动模糊图像复原
估计出PSF参数后,本文采用维纳滤波对运动模糊图像进行复原,维纳滤波以复原图像(x,y)和原始图像f(x,y)的均方误差最小为原则进行图像复原。误差量的表达式如下
e2=E{(f(x,y)-(x,y))2}
(12)
式中E{·}为参数的期望值。维纳滤波在频率域中表示为
(13)
式中Sn(u,v)=|N(u,v)|2为噪声的功率谱,Sf(u,v)=|F(u,v)|2为原始图像的功率谱,Sn(u,v)/Sf(u,v)用常数K表示为
(14)
K取值范围为0~1。对图1(b)(模糊尺度为20像素,模糊角度为60°,高斯噪声为0.002)进行维纳滤波复原,分别取不同K值,直观复原效果如图5所示。可见,K值取0.01时复原效果最好,此时图像峰值信噪比(peak signal to noise ratio,PSNR)最高,为21.765 6。

图5 不同K值维纳滤波复原效果对比
2 指针式仪表读数识别
2.1 仪表检测与读数
本文采用最大类间方差(OSTU)算法进行图像分割,利用类别方差作为判据,能够自适应确定图像的全局最佳阈值,使前景与背景被错误分割的概率最小[14]。图5(c) 二值化后结果如图6(a)所示。对仪表图像进行图像细化(又称为图像骨架化)[15],以大大降低表盘及指针提取特征的难度。对二值化的仪表图像进行形态学细化后如图6(b)所示。

图6 仪表表盘与指针检测
本文通过Hough变换检测图像中表盘所在的圆,将图像空间中的边缘点映射到参数空间中,对在参数空间中获得的所有坐标点对应的累加值进行累加统计,进而检测出圆心的位置及圆的大小[16]。表盘检测结果如图6(c)所示。仪表指针检测可通过Hough直线检测实现,将图像坐标系内经过一点的直线信息转换为该直线法线在极坐标空间中的信息。指针检测结果如图6(d)所示。
检测出表盘及指针后,可通过角度比例关系得到仪表的读数
(15)
式中β为指针偏转角度,βA为起始刻度的角度,βB为终止刻度的角度,T为仪表量程。
2.2 仪表读数实验
统计10组不同示数的产生运动模糊的仪表图像,用本文算法进行仪表识别读数,实验结果如表4所示。
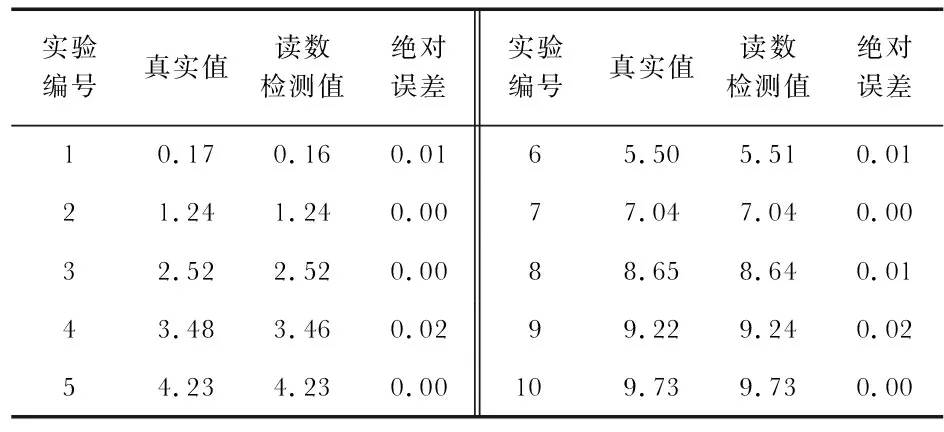
表4 仪表读数实验结果
3 结 论
1)提出一种图像分块结合Canny边缘检测、改进的模糊图像PSF的模糊参数估计方法,并采用维纳滤波实现图像复原。
2)通过对仪表图像进行二值化与图像细化再处理,采用Hough变换实现仪表表盘及指针提取,并基于角度与量程信息完成自动读数。
3)典型实验结果表明:本文方法可以提高PSF参数估计的准确率,对运动模糊仪表图像具有较高的识别精度。运动模糊角度估计误差在2°以下,模糊尺度估计误差在2像素以内;平均绝对误差为0.007,最大误差为0.02。
