基于格拉布斯准则的膛压测试仪校准数据拟合方法*

郝旭娥， 沈大伟， 张艳兵， 黄福峰

(1.中北大学 电子测试技术重点实验室，山西 太原 030051； 2.辽沈工业集团有限公司,辽宁 沈阳 110045)

0 引 言

火炮膛压测试对检验火炮性能十分重要[1]。用静态标定的测压器由于高温高压等环境力的作用存在实测不准或测试精度不高等问题，于是采用环境因子的准静态校准方法，对膛压测试仪实施校准[2，3]，并对校准数据进行拟合来获得灵敏度系数。灵敏度系数是通过对校准的数据拟合而来，所以选取数据拟合的方法至关重要。文献[4]将校准数据用最小二乘(least square,LS)法拟合，但是其描述的系数矩阵是固定的，没有考虑随机误差；文献[5]将LS法与整体最小二乘(total LS,TLS)法拟合对比，并通过实验证明TLS法的拟合精度更高，但是没有考虑粗差的影响；在实际试验中，人为、仪器以及环境的影响，不可避免的系数矩阵也含有误差，甚至有一定量的粗差，为解决这些不足，本文提出了在TLS法的基础上采用格拉布斯准则的算法。

1 模拟膛压校准系统

1.1 校准系统的组成和原理

校准系统主要包含模拟膛压发生器、标准测压系统和高低温试验箱三大部分[6]，其示意图如图1所示。校准时先将测压器放进模拟膛压发生器内，接着经点火装置点燃发射药[7]，在模拟膛压发生器的腔体内产生与火炮膛内相似的高温、高压环境，产生的压力共同作用在标准压力传感器和被校准的测压器上，然后二者同时采集信号，待信号记录完毕，在计算机上读出测压器数据[8]。把多次校准的测压器数据和标准测压系统的数据进行处理，获得被校准测压器的工作直线方程。

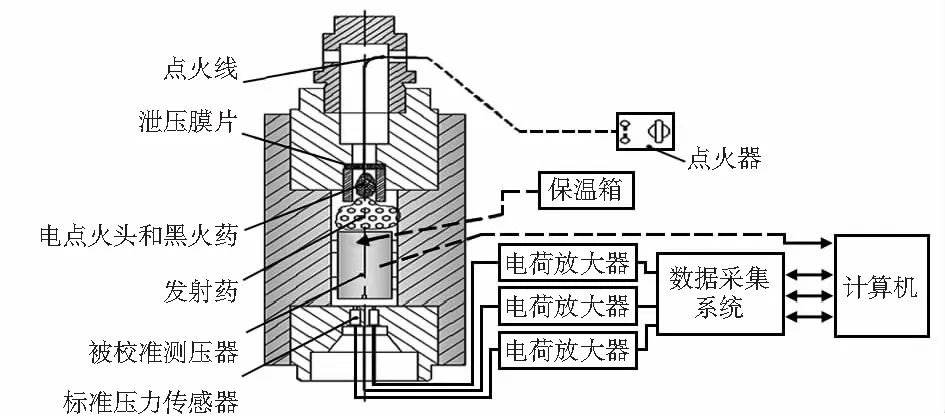
图1 火炮膛压测试模拟环境因子的校准系统组成示意

1.2 基于上升沿校准数据的线性拟合

膛压测试仪基于压力曲线上升沿的校准过程是：选择测压器满量程的95 %～100 %的压力值作为校准点，分别在低温(-40 ℃)、常温和高温(55 ℃)下各获得10组有效数据[9]。在同一直角坐标系下，以标准测压系统的平均压力曲线为基准，逐点平移测压器曲线，当二者具有最大的相关系数时，在曲线峰值压力30 %～80 %压力范围内，对应取n对数据(y1,x1)，(y2,x2)，…，(yn,xn)[10]。在某温度环境下重复10次校准试验，把从10组压力曲线中得到的所有的数据样本进行线性拟合，从而获得测压器在该温度下的工作直线方程[11,12]

y=ax+b

(1)

式中y为该测压器某温度下某数据点的压力，MPa；a为该工作方程的灵敏度系数，MPa/bit;b为该工作方程的截距，MPa;x为某数据点的bit值。

2 本文算法

2.1 TLS法原理

TLS法考虑到数据在x，y两个方向的观测误差，其误差方程可写为[13～15]

yi+vyi=a(xi+vxi)+b

(2)

其约束准则为

(3)

利用拉格朗日乘数法进行解算，则构成的目标函数为

2∑λi(yi+vyi-a(xi+vxi)-b)

(4)

式中λ为拉格朗日乘积因子，对式(4)中的各待估计量求偏导得

(5)

式中 带小冒的量表示估计量。综合式(5)可以得到

(6)

由式(6)可得参数b的估计公式为

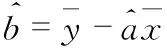
(7)

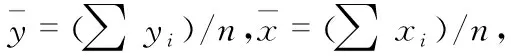
(8)

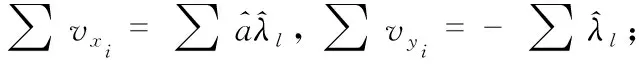
式(8)可进一步简化为

(9)

整理式(9)，可以得到

(10)

单位权方差的计算公式为

(11)

2.2 格拉布斯准则

对一组服从正态分布的数据x1,x2,x3,…,xn按大小顺序排成顺序统计量x(i)，然后利用式(12)计算标准偏差δ，利用式(13)计算g1和gn的格拉布斯值[16,17]

(12)

(13)

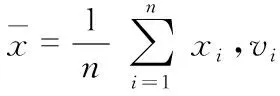
2.3 基于格拉布斯准则的TLS法

格拉布斯准则是对一组一维数据进行异常值判定，但本文的背景是一元线性拟合，是一组二维数据，所以本文先将数据进行预处理，再利用准则，其算法步骤如下：

1)利用TLS法拟合出待估参数a,b的值。

2)计算每个校准点到拟合工作直线的距离di

(14)

3)计算标准偏差δ

(15)

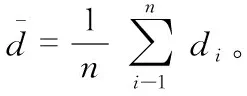
4)将服从正态分布的di的数据按从小到大的顺序排列，并利用公式Gi=(di-)/δ计算G1和Gn。

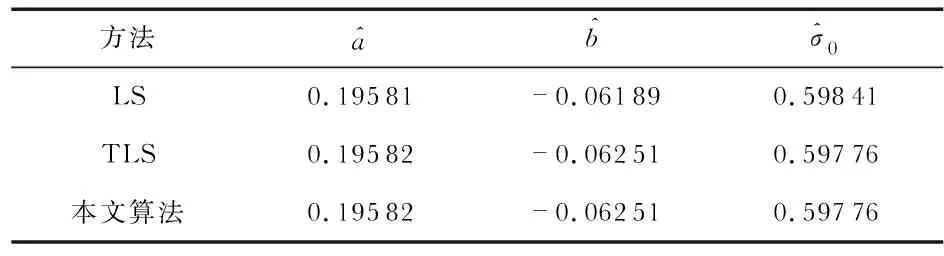
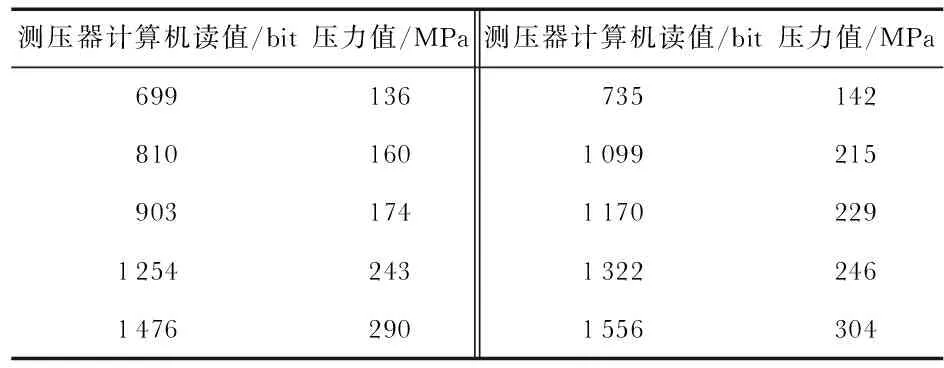
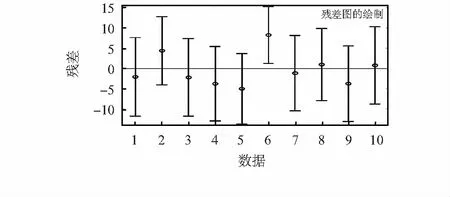
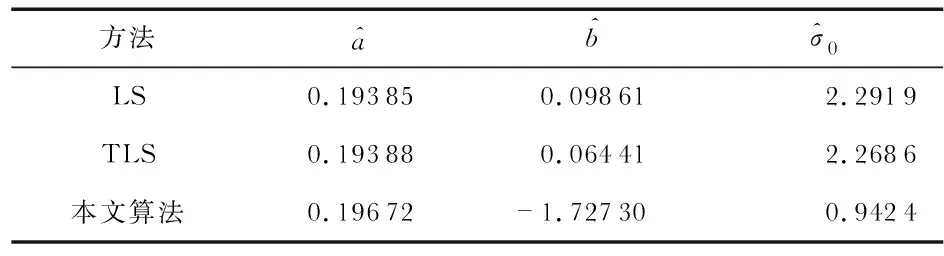
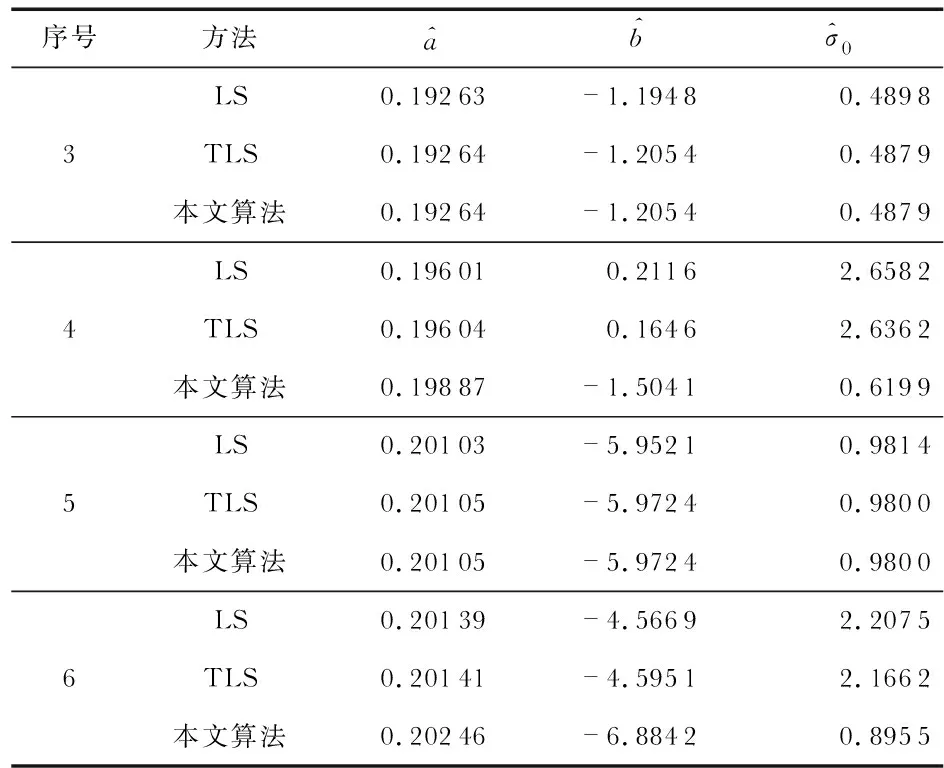
5)查表获取临界值Gp(n)，一般取置信概率P=0.95，若G1≥Gn,且G1>Gp(n)，则d1为异常点，剔除；Gn≥G1,且Gn>Gp(n)，则dn为异常点，剔除；G1

6)利用TLS法计算待估参数的值。

3 校准数据与拟合结果分析

3.1 观测数据仅含随机误差

以1#测压器在低温条件下10组压力上升沿曲线中的数据(仅含随机误差)为样本进行实验，数据如表1所示，其残差图如图2所示。

表1 1#测压器校准数据

图2 1#测压器校准数据残差

分别采用LS法、TLS法和本文提出的算法三种方法对实验数据进行拟合，其拟合结果如表2所示。

表2 1#测压器拟合结果

从表2可以看出,TLS法和本文算法的结果完全一样，且单位权重误差比LS法的小，这是因为当观测数据仅存在随机误差时，采用格拉布斯准则对数据进行检验时，没有异常值，所以拟合方法和TLS法一样；基于Gauss-Markov模型的LS法仅对于观测向量进行约束，要求观测值残差平方和最小，而基于EIV模型的TLS法对误差中所有受误差干扰的随机变量进行约束，所以精度比LS法的高。

3.2 观测数据包含随机误差和粗差

对2#测压器在低温条件下进行校准，其校准数据(有粗差)如表3所示,其残差图如图3所示,分别用三种方法拟合的结果如表4所示。

表3 2#测压器校准数据

图3 2#测压器校准数据残差

表4 2#测压器拟合结果

从表4可以看出,本文算法的拟合精度最高，单位权重误差最小。这是因为当观测数据不仅存在偶然误差，也有粗差时，LS的平方差不能有效区别偶然误差和粗差，对误差的分配具有公平性，其平方差结果将严重受到粗差的干扰；而本文算法在TLS法改正系数阵的基础上，利用准则还可以将有粗差的数据剔除掉，从而在一定程度上减弱了误差的影响，提高了拟合精度，获得了较好的拟合参数。

3.3 多组传感器的校准数据拟合

分别对4只传感器的数据进行拟合，来证实这一结论，其拟合结果如表5所示。

表5 三种方法拟合结果

表5中3#和5#的校准数据仅含偶然误差，4#和6#两组在偶然误差的基础上还有粗差，由表5可知,不管观测数据有没有粗差，本文提出的算法拟合精度最高，证实了该算法的可靠性。

4 结 论

本文针对膛压测试仪模拟应用环境下的准静态校准数据存在偶然误差，甚至有异常数据的问题，提出了将Grubbs准则和TLS法相结合的算法，试验结果表明:该算法提高了拟合数据的精度，获得了较好的灵敏度系数，而且算法简单实用，很适合在膛压测试仪校准过程环境中使用。但本文提出的算法每次只能对一个粗差数据进行剔除，如何一次性筛选出所有异常值有待进一步研究。