依据加权Delaunays三角网的林分空间结构分析与评价1)

孙宇 刘盛 王诗俊 赵士博 李恩鹏 罗见 田佳歆 程福山

(北华大学，吉林市，132013)

林分空间结构是林木在林分中的分布状态，包含林木相对位置及属性在空间的排列方式，能反映出林木之间的竞争关系、混交关系与分布的格局[1-2]。林分空间结构影响着林分的稳定性、林木生长状态和林分生产力大小[3]，因此只有客观准确的了解林分空间结构，才能为后续的经营奠定理论基础。现阶段对于林分空间结构的研究多数学者往往采用不同的能描述林分状态的林分参数，比如由惠刚盈等[4-8]提出的大小比数、混交度、角尺度等参数，通过构建一个固定株数的林分竞争单元，分析林分空间结构的分化程度、混交程度和均匀程度。这些参数的计算基础是林分竞争单元的确定，我们通常将对象木和与对象木存在竞争关系的竞争木所构成的一个小群体称为林分竞争单元，由1株对象木和n株竞争木组成[9]。如何在复杂的林分环境中准确确定竞争木株数，从而全面准确的把握林分结构特征，是林分空间结构研究的重点。

根据惠刚盈等[4-8]的研究，在每一株对象木的周围选取4株竞争木构成一个竞争单元，这种确定林分竞争单元的方法在外业调查时容易操作，但是该方法有一定概率把距离较远无竞争关系的林木当做竞争木，或者因固定竞木数量限制不能把所有竞争木加入竞争单元。汤孟平等[10]使用ArcGis软件中的Voronoi图来确定林分竞争单元，通过现阶段学者的研究进展可以证明Voronoi图相比较传统4邻近木方法，可以更加灵活地定位林分竞争单元，但是Voronoi图没有考虑林木胸高、冠幅、树高，有时会误判对象木的影响范围[11]。赵春燕等[12]利用Voronoi图和Delaunay确定林分竞争单元，Delaunay三角网其实是一种三角剖分算法，在林业中它根据对象木点有效范围来计算竞争木，具体方法是在ArcGis软件中通过计算平面上每个离散点(对象木)的有效范围来确定竞争木数量[13]，该方法同样没有考虑林木的胸径、冠幅、树高因子，在确定林分竞争单元时存在一定偏差。如何在林分空间结构中准确判定林木之间的竞争关系，是现阶段研究的重点和难点。为了修正对象木与竞争木之间的竞争关系，本文将每株林木的胸径、树高、冠幅换算成度量单位一致的权重并以距离的形式加权到Delaunays三角网中，在林木权重的赋予上，刘玉平[14]和李丹学者[15]采用固定权重法，该方法对林木所处竞争环境的描述不具有全面性。本文首次采用林木所处大环境和小环境权重两者相结合的方法，灵活精准确定每株林木胸径、树高、冠幅权重，提高了林分竞争单元中对象木定位竞争木的精准度，在一定程度校正了Voronoi图误判对象木影响范围的缺点[16]，从而使得林分空间结构参数的计算结果更加准确。以加权三角网计算的6个林分空间结构参数为基础，在前人研究的基础上[17]结合落叶人工林分空间结构特点构建了林分经营迫切性评价体系，对20块样地进行经营迫切性评价与分析。期望本文构建的从林分竞争单元精准确定到林分空间结构参数选择及林分经营迫切性评价的一整套方法能够为林分空间结构研究，为森林的可持续经营提供理论基础与技术方法。

1 研究区概况

试验样地位于吉林省白山市抚松县露水河林业局东升林场。地理坐标为128°4′～128°16′E，46°55′～47°2′N。属于温带季风气候，冬季寒冷干燥，夏季多雨潮热，年平均气温4 ℃，年平均日照2 400 h，年平均积温2 400 ℃，年均降水量800 mm左右。该地区主要植被有红松(Pinuskoraiensis)、落叶松(Larixgmelinii)、色木槭(Acerpictum)、忍冬(Lonicerajaponica)、胡枝子(Lespedezabicolo)、白桦(Betulaplatyphylla)、水曲柳(Fraxinusmandshurica)、胡桃楸(Juglansmandshurica)、黄檗(Phellodendronamurense)、红松(Pinuskoraiensis)等。样地属于落叶松人工林，由于造林初期落叶松成活率不高，导致样地内天然更新了大量白桦、椴树、水曲柳等阔叶树及少量的红松，形成了以落叶松为优势树种的针阔混交林。

2 研究方法

2020年11月至12月期间，对露水河林业局东升林场进行较为全面的踏查后，使用全站仪设立了20块面积为0.06 hm2正方形样地，对林内超过5 cm胸径的林木进行每木检尺、挂牌、记录其空间相对位置，样地基本信息如表1。

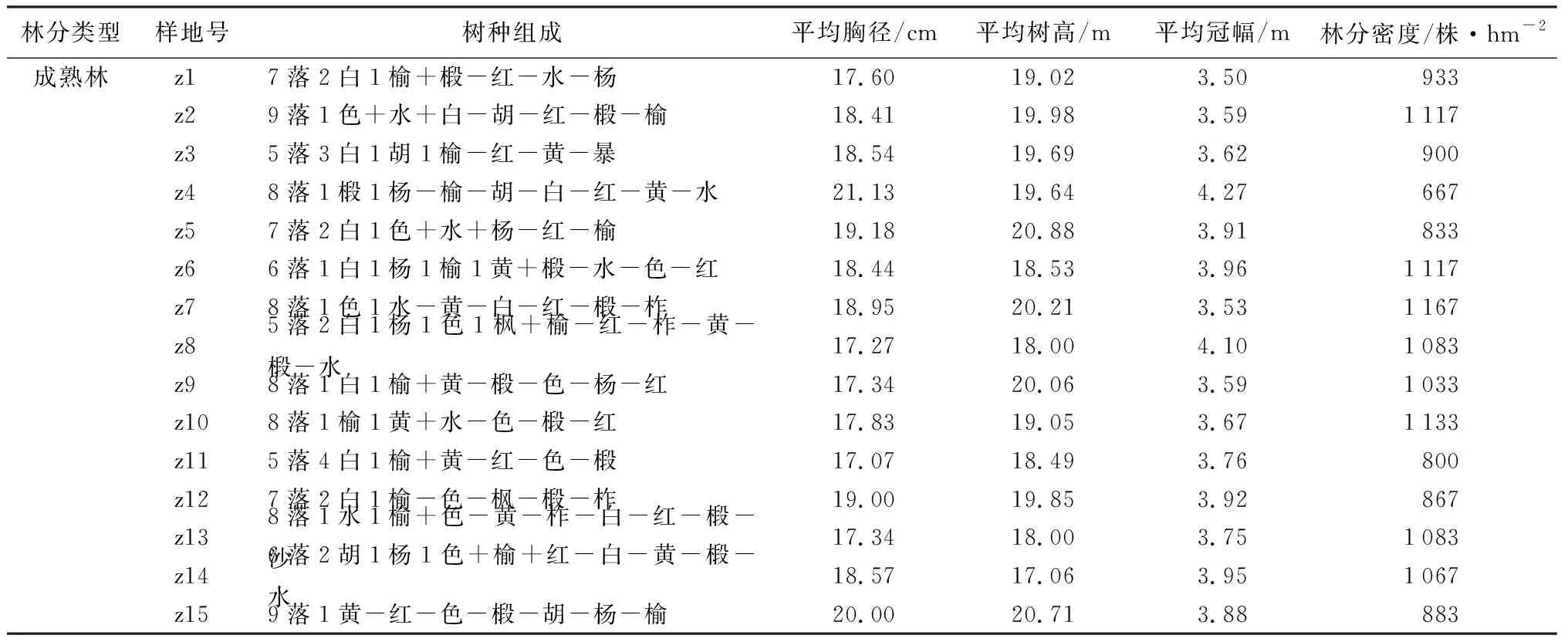
表1 各样地基本概况

续(表1)

2.1 加权三角网的构建原理与林分竞争单元的确定

在ArcGis软件Delaunays三角网中根据对象木与竞争木之间的竞争关系虚拟其之间的距离，生成加权Delaunays三角网以提高对象木定位竞争木的精度，具体方法如下：

将20块落叶松人工林样地根据林木坐标位置，在ArcMap软件中生成常规Delaunays三角网并确定林分竞争单元，如图1所示，以林木的胸径、树高、冠幅为权重对其进行加权，把林木的树高、胸径、冠幅参数通过公式(1)换算成度量单位一致的数值λi。

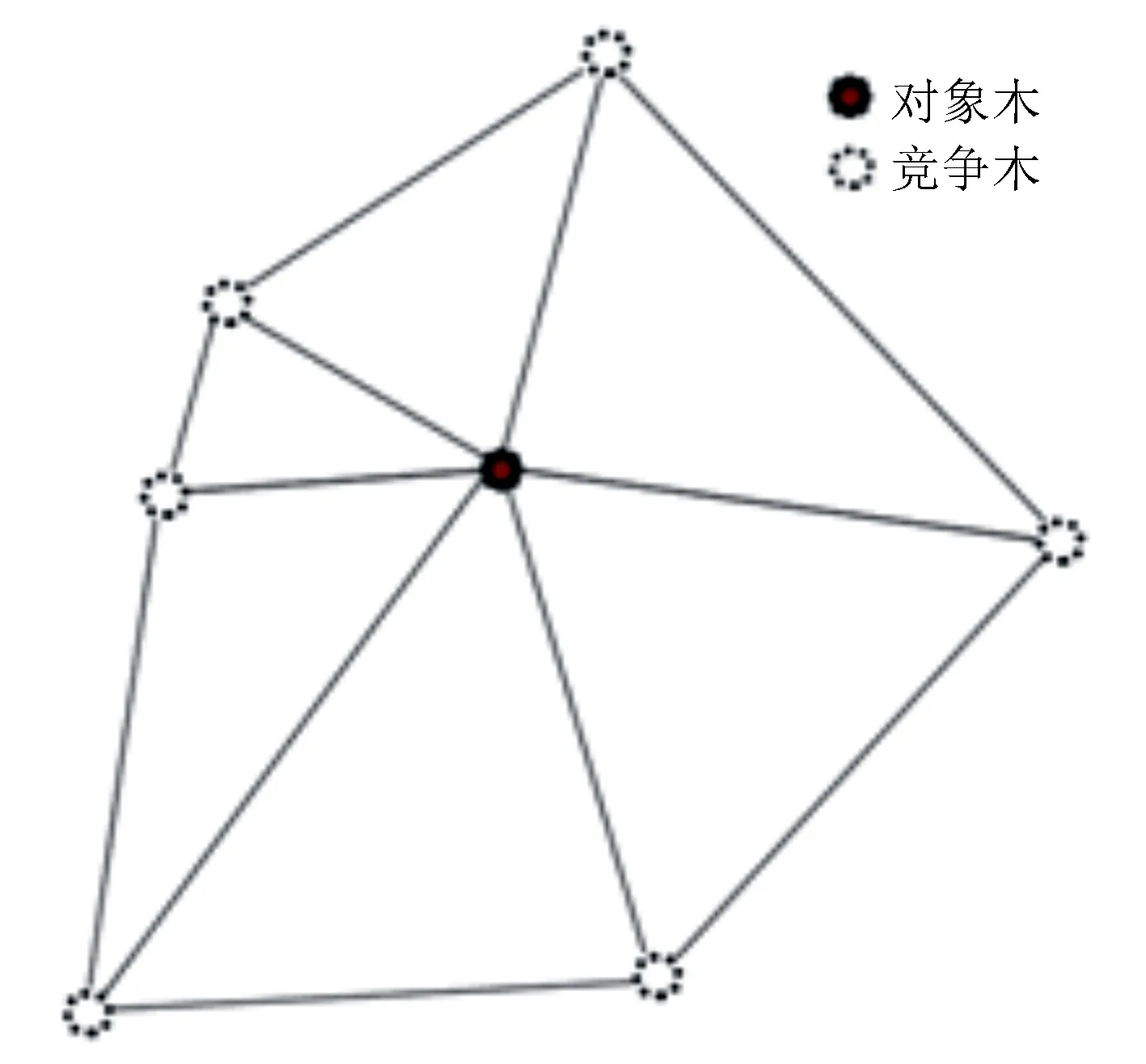
图1 林木空间结构单元

(1)

WKDi=KDi÷(KDi+KHi+KCWi)，

(2)

WKHi=KHi÷(KDi+KHi+KCWi)，

(3)

WKCWi=KCWi÷(KDi+KHi+KCWi)。

(4)

在公式(2、3、4)中：KDi、KHi、KCWi分别为对象木i所处小环境中胸径、树高、冠幅的优势度，计算公式(5、6、7)。

(5)

式中：KDi取值，当竞争木j的胸径小于对象木i胸径时mij=1、否则mij=0。

(6)

式中：KHi取值,当竞争木j的树高小于对象木i树高时qij=1、否则qij=0。

(7)

式中：KCWi取值，当竞争木j的冠幅小于对象木i冠幅时nij=1、否则nij=0。

公式(5)中：KDi为对象木i在小环境中胸径的优势度，取为值范围是数值0到1之间，数值越大表示对象木在小环境中优势越大，从而所占权重越大。公式(6)中：KHi为对象木i在小环境中树高的优势度，取为值范围是数值0到1之间，数值越大表示对象木在小环境中优势越大，从而所占权重越大。公式(7)中：KCWi为对象木i在小环境中冠幅的优势度，取为值范围是数值0到1之间，数值越大表示对象木在小环境中优势越大，从而所占权重越大。

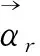
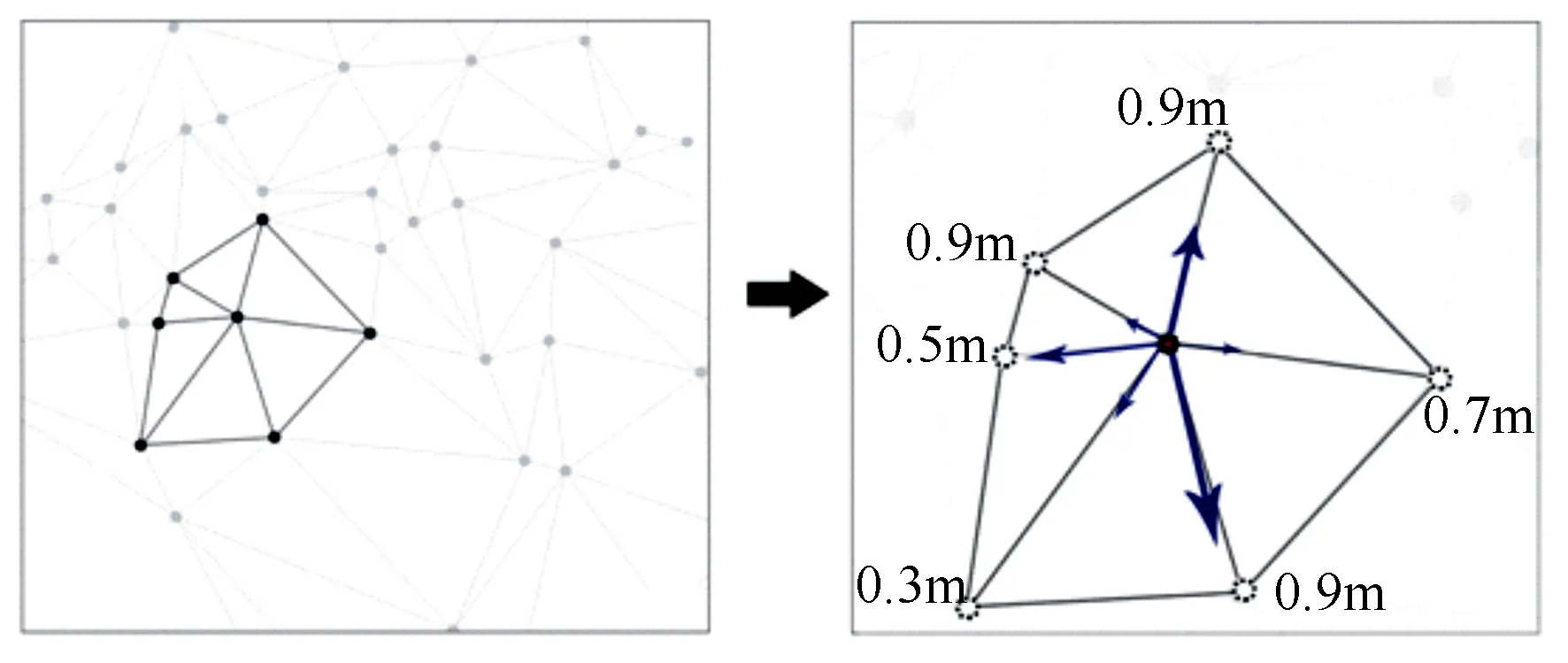
图2 三角网模型的加权原理

(8)

(9)

加权Delaunays三角网只是用ArcGis软件虚拟对象木与竞争木之间的距离，以提取修正过后的林分竞争单元信息，在实际中林木的坐标位置没有变动。该方法在一定程度上校正了Voronoi误判竞争木的现象，显著了提高对象木定位竞争木的精度，从而能使得林分空间结构参数的计算更加客观准确。对比Voronoi图优点具体：在Voronoi图确定的林分竞争单元中，部分竞争木与对象木之间距离较远且胸径、树高、冠幅等参数均较小，与对象木之间几乎不存在竞争关系，加权Delaunays三角网将对象木与竞争木之间的综合权重转换为虚拟距离，根据距离的远近结合自身算法该判断是否将此竞争木排除竞争单元。同样林分竞争单元中有些对象木与竞争木之间距离比较近并且胸径、树高、冠幅参数均较大，通过加权Delaunays三角网修正，使其之间的虚拟距离缩短。

2.2 消除边缘效应

在样地中的边界处，存在某些对象木的竞争木位于样地外的现象，导致林分参数计算结果出现偏差。因此以消除边缘木为目的，在样地四周设立大于林分平均冠幅半径2 m宽的带状缓冲区[18]，缓冲区的林木只能当作竞争木，如图3所示。

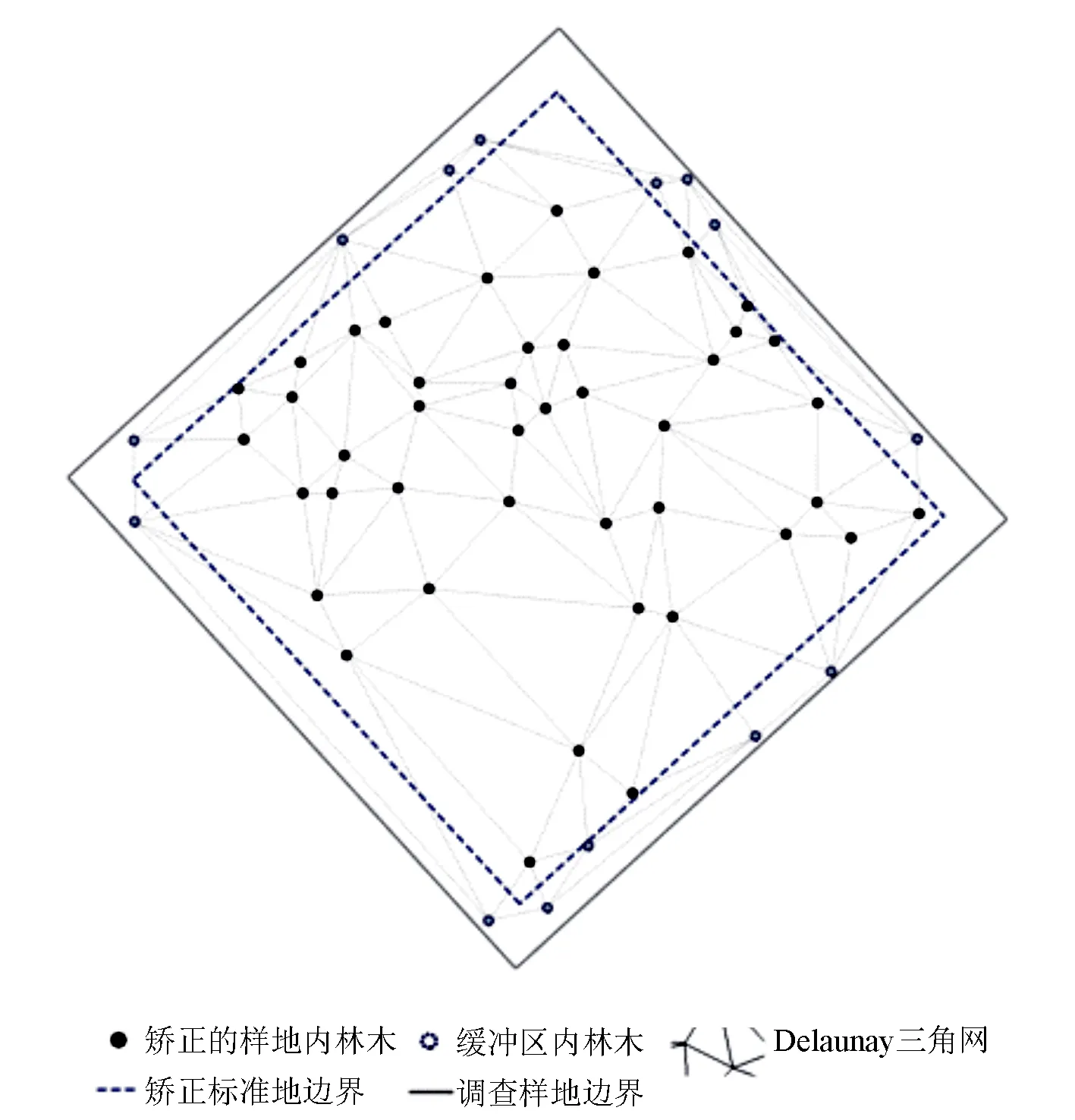
图3 样地边缘矫正结果

2.3 林分空间结构参数选取

本研究采用6个能反映林分空间结构的参数，分别是通过计算林木之间夹角来反映林分水平分布格局的角尺度[19]，与胸径密切相关，能反映出林分大小分化程度的大小比数[20]，以冠幅为基础，说明林木上方空间利用程度的密集度[21]，能反映林木之间竞争的交角竞争指数[22]，说明林木生长空间大小和透光性的开敞度[23]和能反映树种间相互隔离程度的多样性混交度[24]。

角尺度：

(10)

公式10中：Wi为第i株对象木的角尺度数值，取值范围是数值0到1之间，Wi数值越小，表明竞争木围绕对象木i的布局越具有平均性，否则反之，如图4所示。标准角α取值为360°/(n+1)[25]。

图4 林分竞争单元角尺度

图4中，字母Q代表对象木，数字1、2、3、4代表竞争木，s1、s2、s3、s4分别代表竞争木4、1，1、2，2、3，3、4以对象木为中心点生成的夹角。

大小比数：

(11)

公式(11)中：Ui为第i株对象木的大小比数，取值范围是数值0到1之间，Ui数值越小，表示比对象木大的竞争木越少，否则反之。

密集度：

(12)

公式(12)中：Ci为第i株对象木的密集度，取值范围是数值0到1之间，Ci数值越小，表明对象木冠幅生长空间越充足，否则反之。

开敞度：

(13)

公式(13)中：Ki为第i株对象木的开敞度，Ki∈(0，+∞]，Ki数值越大，表明对象木生长空间越充足，否则反之。Dij为对象木i与竞争木j之间的距离，Hij表示竞争木j的树高。

竞争指数：

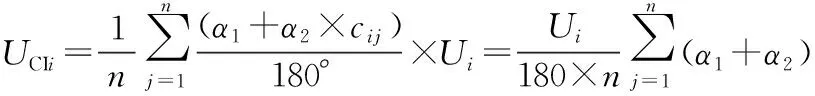
(14)

公式(14)中：UCIi为第i株对象木的竞争指数，取值范围是数值0到1之间，UCIi数值越小，表明对象木受到竞争越小，否则反之。Ui为对象木i的大小比数，Hi表示对象木i的树高，Hj表示竞争木j的树高，Dij为对象木i与竞争木j之间的距离。

混交度：

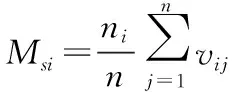
(15)

公式(15)中：Msi为第i株对象木的混交度，取值范围是数值0到1之间，Msi数值越小，表明对象木混交程度越小，否则反之。ni为对象木i所在林分竞争单元中树种数量。

2.4 统计分析方法

2.4.1 加权前后林分参数统计学分析

为了证明加权后林分空间结构参数统计学意义没有变化，计算20块落叶松人工林样地加权前后混交度、开敞度、大小比数、竞争指数、角尺度、密集度的平均值，采用峰度、偏度系数法和柯尔莫哥洛夫-斯米诺夫检验对其进行正态检验，并用斯皮尔曼相关性分析法分析其之间的相关性。

2.4.2 加权前后对象木与竞争木之间竞争关系

判断对象木与竞争木之间竞争关系的有效方法包括：查看二者距离的远近情况及每木检尺数据。为证明加权Delaunays三角网修正了对象木与竞争木之间的竞争关系，计算落叶松人工林样地加权前后林分竞争单元内竞争木位置和数量的变化，统计出加权后林分竞争单元中排除和增加的竞争木株数，通过计算该类竞争木与对象木之间综合权重和距离，验证将其排除和增加的合理性。

2.5 林分经营迫切性评价体系的构建

评价指标的选择：单个的林分空间结构参数不能全面的反映出林分空间结构和竞争强弱，为了解现实林分与理想林分的差距以及综合、全面地对林分整体竞争状态给出评价，基于加权Delaunays三角网本文选择了7个指标，其中5个是林分空间结构参数指标。另外2个指标是以林分空间结构参数为基础运算的目的树种优势度指标(本文为落叶松)、林分空间优势度指标[17]，计算公式分别为(17)、(18)。

(17)

式中：Dsp为落叶松树种优势度；Dg为落叶松占林木总株数的比例；P为落叶松大小比数均值。

(18)

式中：SD为林分空间优势度指标,R表示样地中大小比数为0的林木比例，E表示样地中50%最大林木断面积的均值再乘林木总数量。G是样地林木平均断面积。

评价的方法：利用上述7个指标，参考前人的研究[17]以及结合落叶松人工林空间结构特点，建立了林分经营迫切性评价指标体系及标准，如表2所示，结合公式(19)计算出林分迫切性评价指数。参照孙培琦等[17]提出的经营迫切性等级划分标准对样地划分评价等级，该标准基于林分空间结构和林分整体竞争状态把林分划分为5个等级，等级越高说明林分需要经营的迫切性越高。Ⅴ级林木空间结构极为不合理、林木间竞争极为激烈，极需抚育经营；Ⅰ级林木空间相对合理、林木间竞争不强，林分稳定且暂不需抚育经营。

表2 林分经营迫切性评价指标体系及标准

(19)

3 结果与分析

为了分析6个空间结构指标加权和不加权所得到的结果是否具有统计意义，利用加权前后20块落叶松人工林样地林分参数平均值，采用峰度、偏度系数法和柯尔莫哥洛夫-斯米诺夫检验对其进行正态检验，并用斯皮尔曼相关性分析对其进行验证。结果表明：加权前后的林分参数均符合正态分布，统计学意义没有发生变化，可以进行下一步分析，分析结果如表3所示。在相关性分析中除了角尺度加权前后不相关，其余参数均显著相关，如表4所示。这是因为加权后的林木坐标会根据对象木与竞争木之间的权重变动，坐标的变动会引起林木之间夹角和标准角的变动，从而影响林分参数计算结果，但是基于加权三角网计算的角尺度考虑了林木之间的竞争强弱，能较为真实的描述林分空间结构。

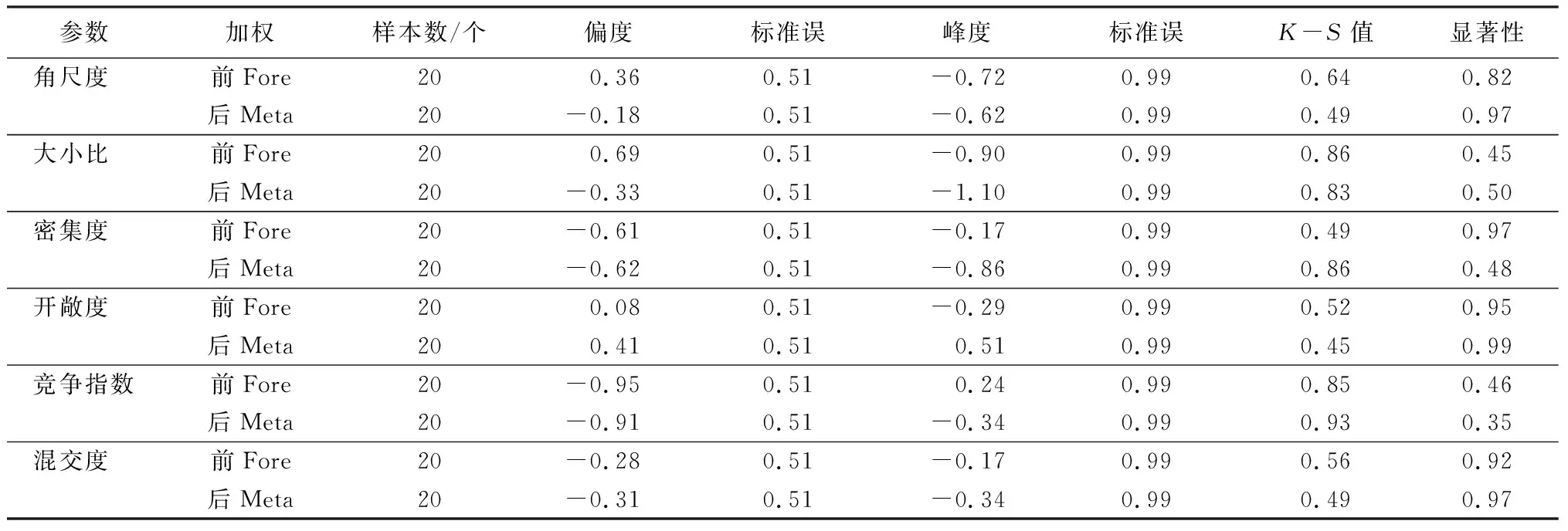
表3 各空间结构参数加权前后正态分布检验结果统计

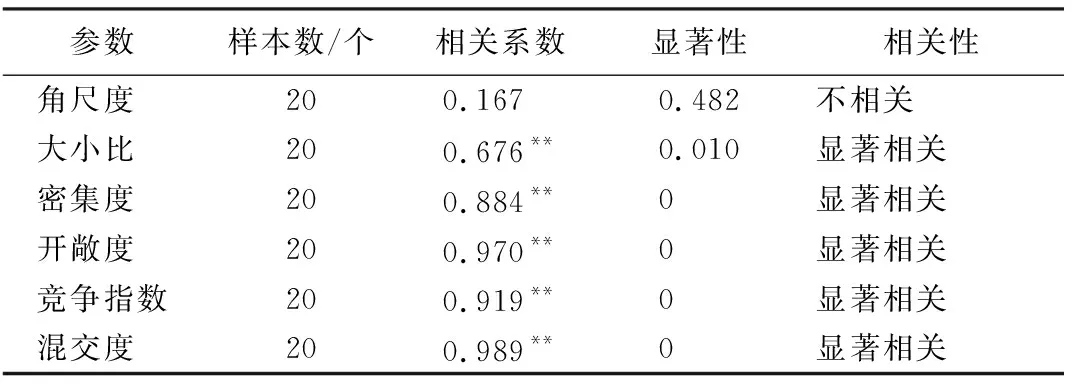
表4 加权前后各空间结构参数相关性分析结果

加权Delaunays三角网的实质是通过虚拟距离来修正对象木与竞争木之间的竞争关系，从而提高对象木定位竞争木的精准度，该方法可以排除林分竞争单元中与对象木之间综合权重较小且距离较远的竞争木，这类竞争木与对象木几乎不存在竞争关系。加权Delaunays三角网也会根据林木间的权重使林分竞争单元中加入与对象木存在竞争关系的竞争木，如图5所示。

Q代表中心木，1、2、3、4、5、6、7分别代表竞争木，圆代表树木的冠幅。6号竞争木距离对象木Q比较远且两者之间综合权重较小，使得加权后其之间距离增加并将其排除林分竞争单元。7号竞争木在常规三角网中没有被纳入对象木Q的竞争单元，但是已经和Q形成了竞争关系，经过加权Delaunays三角网修正后，使其加入对象木Q的林分竞争单元中。图5 竞争木变化情况

为了验证加权处理修正了对象木与竞争木之间的竞争关系，计算20块落叶松人工林样地加权前后林分竞争单元中竞争木株数与位置的变化，统计出加权后林分竞争单元中排除和增加的竞争木株数，结果显示：加权前后林分竞争单元的平均竞争木数量分别为5.38和5.40，在加权过程中林分竞争单元中平均排除了1.36株竞争木，根据数据显示，该类竞争木与对象木的平均距离为4.02 m，而样地中竞争木与对象木的平均距离为3.67 m，相差0.35 m，并且该类竞争木与对象木之间权重λij均值小于1，说明加权后被排除的竞争木与对象木之间几乎不存在竞争关系。在加权后林分竞争单元中平均增加了1.37株竞争木，该类竞争木与对象木之间综合权重均值λij大于林分λij的均值，说明加权后加入林分竞争单元的竞争木与对象木存在一定的竞争关系。

为了评价林分是否需要进行抚育经营，本文以落叶松人工林样地加权前后5个林分空间结构参数、林分空间优势度、目的树种优势度这7个指标为基础，参考前人的研究[17]以及结合落叶松人工林空间结构特点，建立了林分经营迫切性评价指标体系及标准。使用公式(19)计算出林分迫切性评价指数，参照孙培琦等[17]提出的经营迫切性等级划分标准对样地划分评价等级，结果显示：加权后较加权前2块样地评价指数降低，1块样地指数升高，其余样地评价指数没有变动，如表5所示。参照加权前后对象木与竞争木之间竞争关系的分析，可以证明，基于加权后构建的林分经营迫切性评价方法，可以从林分空间结构的角度，考虑现实林分与理想林分的差距，全面地对林分整体竞争状态给出评价。

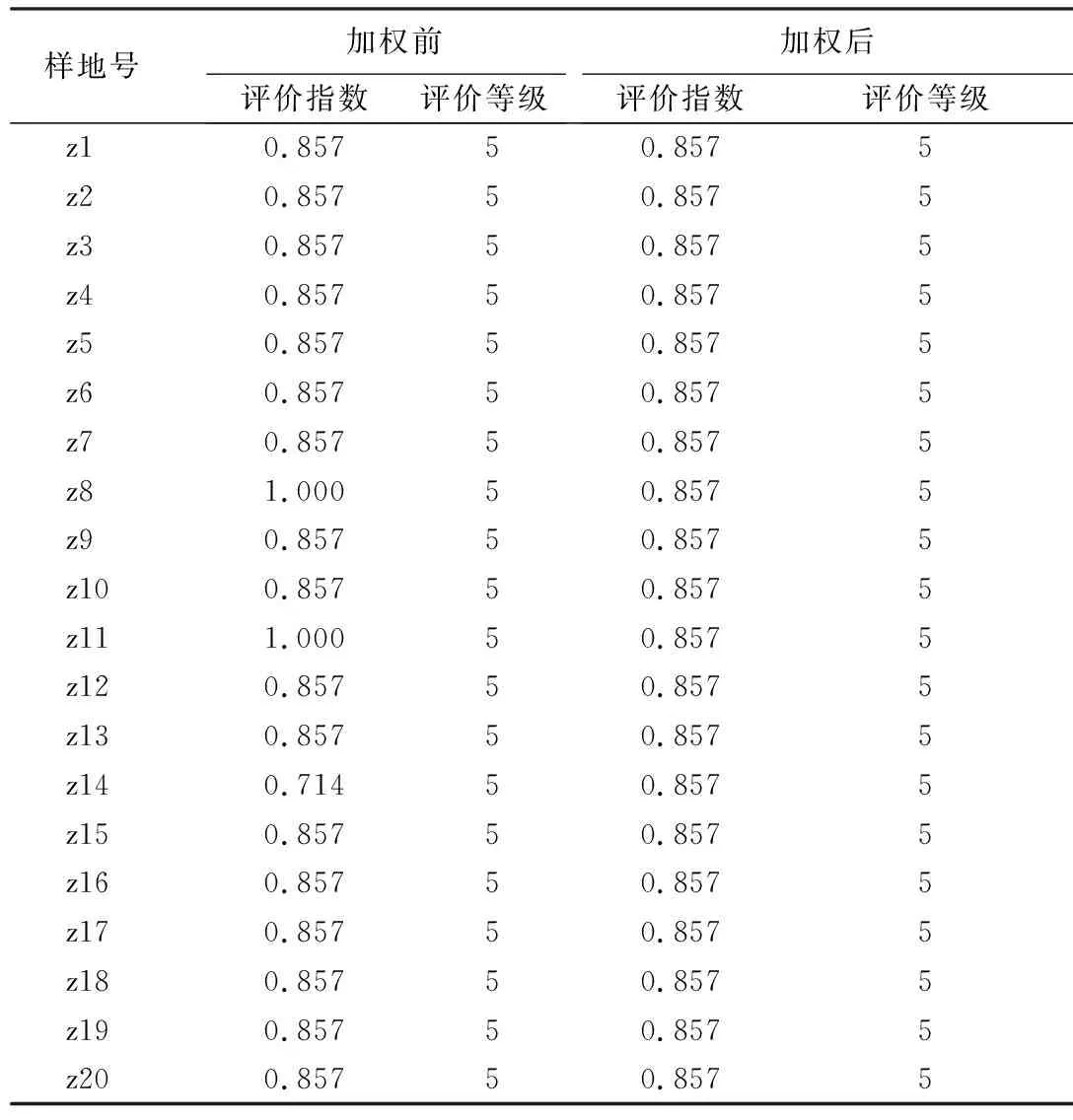
表5 加权前后落叶松人工林经营迫切性评价结果

样地迫切性评价结果说明，林分整体状态不佳，与理想的林分存在很大差距。因样地起源是落叶松人工林，林分树种组成简单，落叶松占据绝对数量优势，密集度指数较高导致林下光环境差。另外，样地中林木不是理想的随机分布格局，林木间整体竞争较大且林分整体优势度小，林分中出现红松、白桦等伴生树种，对落叶松形成一定竞争，但是一定程度上也增加了林分的物种多样性。

4 讨论

本研究采用峰度、偏度系数法和柯尔莫哥洛夫-斯米诺夫检验，对加权前后样地林分参数进行正态检验，所得结果显示林分参数均呈正态分布，这与刘玉平等[16]研究一致，说明在林分空间分析中，将林木权重转换成虚拟距离并加权到Delaunays三角网中，其结果统计学意义没有变化。采用斯皮尔曼相关性分析对加权前后林分参数进行检验，结果显示除了角尺度加权前后不存在相关性，其余参数均呈显著相关，与李丹[15]的研究结果存在差异，这可能是因为Hegyi竞争指数和本文采用的交角竞争指数存在一定差异所导致的，交角竞争指数能反映林木上方和侧面的竞争情况，本文把胸径、树高、冠幅加权到Delaunays三角网中能较为真实的反映林分竞争单元中竞争情况，因此本文中加权前后竞争指数存在相关性。本文只把林木的胸径、树高、冠幅加权到Delaunays三角网中，却忽略了林木的健康状态、树龄、树种等数据，如果读者能把更多林木参数加权到Delaunays三角网中，也许能够更加全面地描述林分空间结构。在胸径、树高、冠幅权重的确定上，本文把单木在全林分所占权重和单木在小环境所占权重相结合，构建了新的权重赋予方法，显著修正了对象木与竞争木之间的竞争关系，而刘玉平学者[16]认为胸径、树高、冠幅三者权重相同，李丹学者[15]运用灰色关联法计算3个参数的权重，这两种方法都没有考虑林分竞争单元确定中最重要的一点，即对象木所处小环境的竞争情况，所以导致林分参数计算结果略有不同。在林分空间结构分析中，巫志龙[26]等学者只选取了3个为数不多的林分参数，但是单一的林分参数不能全面地反映出林分的空间结构和竞争强弱，而林分经营迫切性评价方法能够客观准确的反映林分整体竞争状态，同时可以作为林分是否需要经营的指标，所以对加权前后落叶松人工林样地进行林分经营迫切性评价，结果显示：样地均属于Ⅴ级(特别迫切)，这与张连金等学者研究一致[24]，说明我国落叶松人工林与侧柏人工林的林分状态较差，需要进行人工经营，加权后相较于加权前，大部分样地林分迫切性指数不变，2块样地评价指数降低，1块样地指数升高。本文从对象木与竞争木之间的竞争关系这一角度，验证了加权后的评价结果更符合实际林分状态。读者可以对林分空间结构参数使用运筹学中的多目标规划，计算出整个林分的评价指数，进一步验证以加权Delaunays三角网为基础运算的林分迫切性评价结果。希望读者在使用加权Delaunays三角网确定林分竞争单元的基础上，借鉴和敬渊[27]等学者所研究的林分参数一元分布，二元分布、三元分布、四元分布，把两者相结合可以更加准确全面地描述林分空间结构。本文把6个林分参数，在林分空间结构分析上同等对待，但是李建军[28]等学者认为林分参数与整体林分状态的关系应该是有大小顺序的，所以可以采用灰色关联法计算林分参数之间关联系数，从而确定林分参数对林分空间结构影响的大小顺序，为落叶松人工林的经营提供科学的指导。

5 结论

为了验证加权处理修正了对象木与竞争木之间的竞争关系，统计分析样地加权前后林分竞争单元中竞争木株数与位置的变化情况，结果显示：在加权过程中林分竞争单元中平均排除了1.36株竞争木，该类竞争木与对象木的平均距离为相差0.35 m，且该类竞争木与对象木之间权重λij均值小于1，说明加权后被排除的竞争木与对象木之间几乎不存在竞争关系。在加权后林分竞争单元中平均增加了1.37株竞争木，该类竞争木与对象木之间综合权重均值λij大于林分λij的均值，说明加权后加入林分竞争单元的竞争木与对象木存在一定的竞争关系。

计算各样地加权前后的6个林分空间结构参数均值，分别采用峰度、偏度系数法与柯尔莫哥洛夫-斯米诺夫检验对其进行正态检验，并用斯皮尔曼相关性分析对其进行相关性检验。结果表明：加权前后角尺度、大小比数、密集度、开敞度、竞争指数、混交度这6个林分空间结构参数的统计学意义没有变化均符合正态分布。在相关性分析中加权前后的角尺度参数不具有相关性，其他5个参数相关性显著。角尺度不相关的原因可能是加权引起了坐标变动，导致林木之间的夹角和标准角的变动，但是不具有相关性不会改变角尺度参数的统计学意义且加权后更接近真实的林分竞争状况。

以加权前后5个林分空间结构参数、林分空间优势度、目的树种优势度这7个指标为基础，结合前人的研究[17]与落叶松人工林空间结构特点，构建了林分经营迫切性评价体系并对样地进行评价与分析，结果显示：3块样地评价指数出现上下浮动，其余样地指数没有变动。根据上文的分析结论，可以证明以加权Delaunays三角网为基础所构建的林分空间结构评价方法，能够较为客观准确的反映林分整体竞争状态，同时可以作为林分经营迫切性的评价指标。从样地林分迫切性评价结果可以反映出，林木整体状态不佳，与理想的林分存在很大差距，需要尽快对林分采取经营措施以优化林分空间结构。