基于GA–BPNN的圆筒形件多步冲压成形工艺参数优化

白月香，黄昭明，王利，张勇明，沈晨

基于GA–BPNN的圆筒形件多步冲压成形工艺参数优化

白月香1,2，黄昭明2,3，王利2，张勇明1，沈晨2,3

（1.江西交通职业技术学院 机电工程学院，南昌 330013；2.马鞍山市汽车冲压模具先进设计工程技术研究中心，安徽 马鞍山 243031；3.无锡九和模具有限公司技术部，江苏 无锡 214142）

研究精密多步冲压成形过程中圆筒形件出现的成形性问题。基于正交试验设计和极差分析方法、BP神经网络建模以及遗传算法得到最优工艺参数，研究制件成形过程中相关工艺参数对减薄率的影响。通过正交试验设计和极差分析，获得各参数对极大减薄率的影响主次顺序为拉延摩擦因数>拉延压边力>反拉延摩擦因数>反拉延压边力，相对最优工艺参数如下：拉延摩擦因数为0.200、反拉延摩擦因数为0.100、拉延压边力为50 kN、反拉延压边力为30 kN。极大减薄率的仿真极值为0.144 4、极小减薄率的仿真极值为−0.127 7；以极大减薄率为成形质量评价指标，经BP神经网络建模并结合遗传算法寻优，获得最优工艺参数如下：拉延摩擦因数为0.200、反拉延摩擦因数为0.159、拉延压边力为55 kN、拉延压边力为40 kN，极大减薄率预测值（0.134 9）与仿真值（0.140 1）的相对误差仅为3.7%，优化后的制件成形质量良好。所提出的方法对量化调整制件的成形工艺具有良好的工程应用价值。

正交试验；BP神经网络；遗传算法；工艺参数；减薄率

拉延工艺决定了拉延制品的成形性、表面质量和尺寸精度，其设计难度大、技术含量高，是拉延模设计、制造的核心与关键[1-3]。我国模具工业发展对高品质、高精度、高性能拉延模具的设计要求在不断提高，这促使以人工经验为导向的传统设计正全面转向以计算机为主体的仿真驱动设计。智能优化技术作为计算机仿真驱动设计的核心技术，能够有效解决板料成形过程中的众多关键问题。为了在一定程度上解决大空间、非线性、全局寻优、组合优化等复杂问题，大量智能优化方法不断涌现，例如进化类算法、群智能算法、模拟退火算法、禁忌搜索算法和神经网络算法等[4-6]。因具有独特的优点和机制，这些算法得到了国内外学者的广泛关注，掀起了板料成形中多参数耦合、过程参数优化和选择问题的研究热潮，在模面设计、工艺方案设计以及工艺参数优化等方面得到了成功应用[7-10]。

根据成形行业的发展现状以及市场对拉延制品的要求，许多学者开展了智能优化方法在拉延成形方面的应用研究，这对缩短产品的开发周期、快速响应市场、提高产品的精度和质量具有重要的现实意义。邱超斌等[11]结合了GS理论和神经网络遗传算法，优化了某航空深腔型零件拉延成形工艺参数，改善了该零件的冲压成形质量。王泌宝[12]使用BP神经网络拟合了有限元仿真最优拉丁超立方抽样法设计的实验数据，获得了输入、输出的非线性模型，并使用遗传算法得到了多目标的Pareto前沿解，实现了B柱加强板减薄率和增厚率等多个目标的优化。李雷等[13]以起皱、厚度不均匀性、回弹量为优化指标，以上下模间隙、下模圆角半径、拉延筋高度、拉延筋相对位置为优化变量，通过奥氏体不锈钢大型封头拉延成形数值模拟实验，验证了人工神经网络和NSGA–Ⅱ多目标遗传算法优化策略的效果。上述研究主要是应用相关智能算法对各类单工序成形的工艺参数进行较深入的研究，取得了有益效果，但无法预测多步冲压成形中工序间非连续应变路径下的成形性，难以大幅提升板料成形的优化效果。

文中以深筒形特征件为研究对象，以CAE软件AutoForm为平台，针对圆筒形件多步冲压成形过程中出现的成形性问题，在获得合格拉延工艺方案的前提下，基于正交试验设计和极差分析、BP神经网络BPNN建模以及遗传算法（genetic algorithm，GA），研究制件成形过程中的关键工艺参数对极大减薄率和极小减薄率的影响，以期为制件成形工艺参数的量化调整提供参考。

1 冲压工艺设计

圆筒形件采用经过双动拉延冲压成形得到的、厚度=1 mm的冲压用冷轧钢板DC03[14]。图1为圆筒形件的三维数模和零件图，其沿口直径1=152 mm、筒身直径2=108 mm、拉延深度1=35 mm、拉延圆角半径1=3 mm、反拉延台阶深度2=8 mm、反拉延圆角半径2=1.5 mm、筒底圆角半径3=3 mm。圆筒形件拉延凹模圆角半径的确定方法如下：当/0（0为拉延件直径）×100=1～2时，=（6～8）；当/0×100=0.3～1时，=（8～10）；当/0×100=0.1～0.3时，=（10～15）。故凹模圆角半径=8～10 mm，且>1。因此，文中需要先调整的尺寸，再将整形至原尺寸，以此来改善制件在拉延过程中因材料难以流入凹模而发生开裂的现象。同时，应用AutoForm软件的Trim模块反求坯料形状来弱化材料成形过程中的各向异性，进而改善成形制件的沿口“凸耳”现象[14-15]。冲压工艺设计深筒形件的初步成形方案流程如下：OP10落料—OP20拉延—OP30整形—OP40反拉延—OP50整形—OP60切边。具体成形工艺方案如表1所示，对应工艺方案CATIA数模如图2所示。

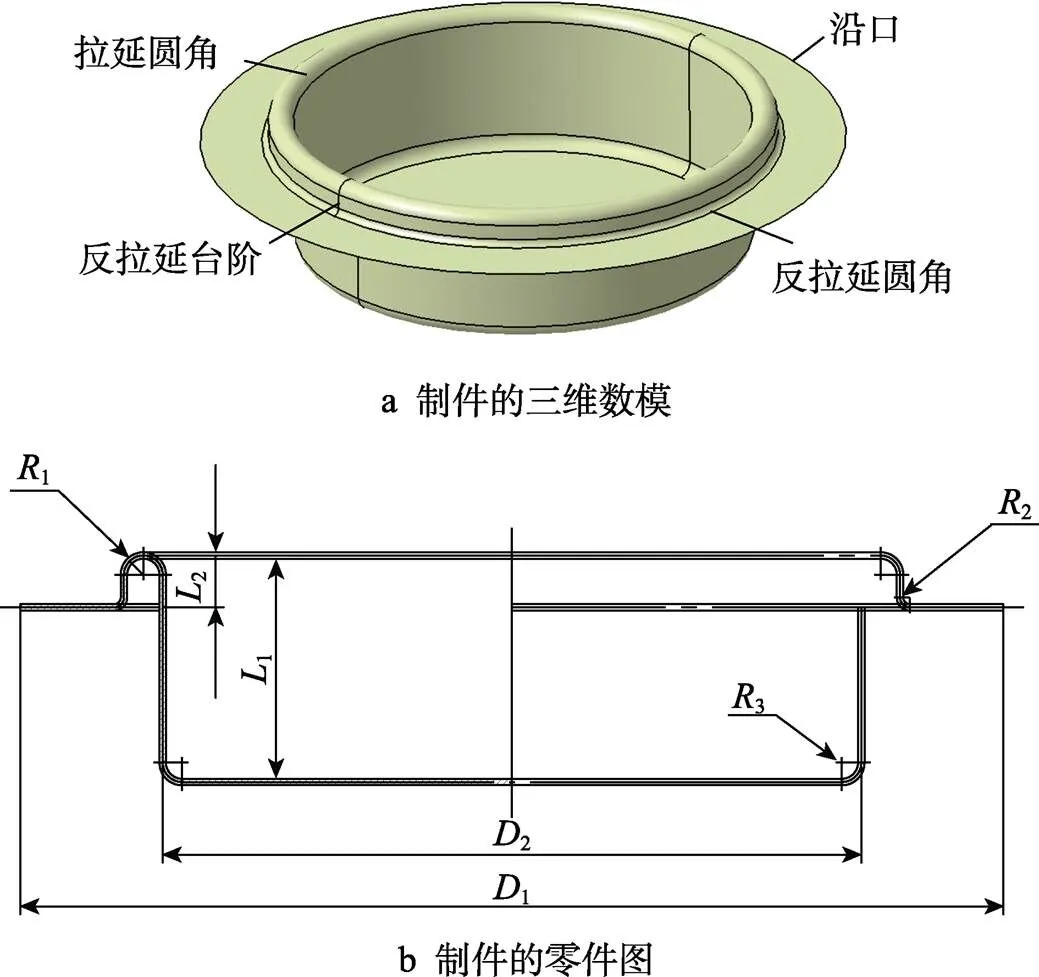
图1 圆筒形件

表1 成形工艺方案

Tab.1 Forming process scheme

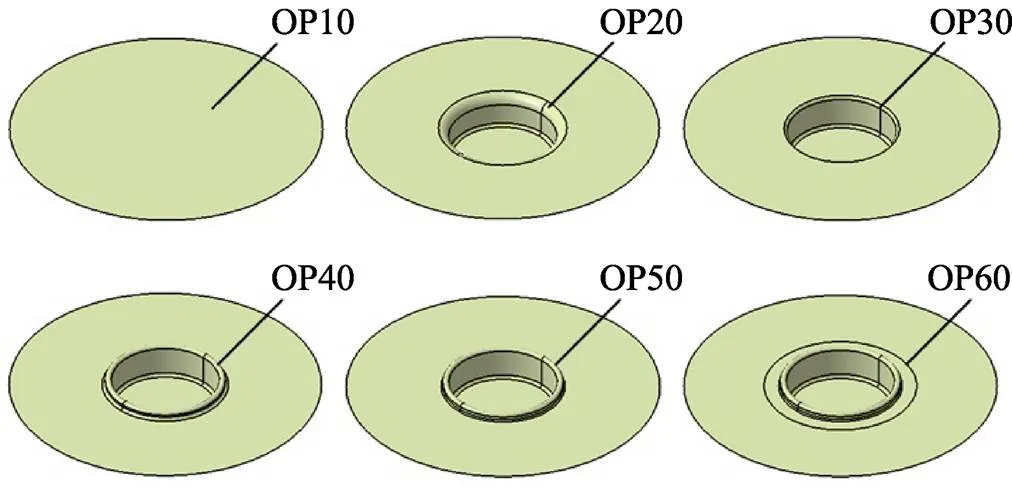
图2 工艺方案CATIA数模

2 有限元建模与仿真

应用AutoForm软件的材料生成器定制DC03部分材料特性，其应力–应变曲线和成形极限曲线如图3所示。DC03坯料的厚度为1 mm，弹性模量为2.1× 10−5N/mm2，泊松比为0.3，屈服面为Hill，双轴应力因子为1.0。

根据文献[14]给出的冲压工艺设计方法，应用AutoForm软件的Trim模块功能获取表1中OP10落料件形状，以圆筒形件的沿口为成形目标边界，反求精度为0.5 mm，进行5次迭代后获得的反求形状如图4所示。应用初步成形方案所建立的全工序法[16-18]设计圆筒形件多步冲压成形三维有限元模型以及运动过程，初步工艺方案仿真结果如图5所示。成形性图中的颜色可以定性地显示制件是否出现起皱、开裂和成形不充分等成形性问题。由图5a可知，圆筒形件的沿口为起皱状态，筒身具有起皱趋势，筒底圆角处为安全状态，筒底为成形不充分状态。因此，得到圆筒形制件的厚度变化规律如下：从沿口至筒底，制件厚度逐步变薄。为进一步定量评估制件是否起皱，由图5b可知，极大减薄率max=0.141 3、极小减薄率min=−0.115 8，这2个值均在结构件安全成形控制要求的±20%范围内[19-20]，故制件不会产生起皱。

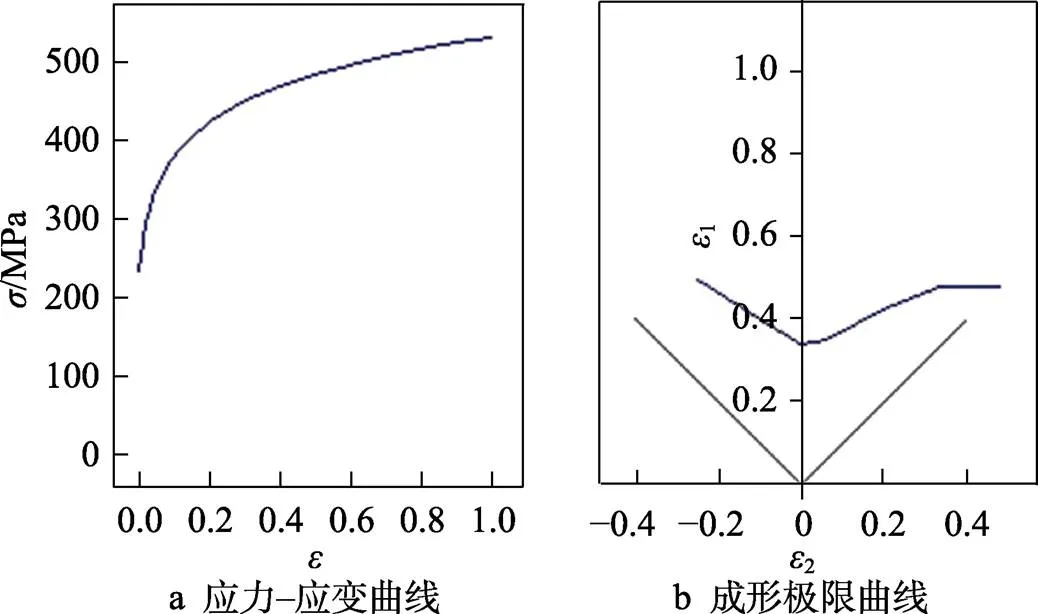
图3 DC03材料的应力–应变曲线与成形极限曲线

图4 Trim模块反求形状

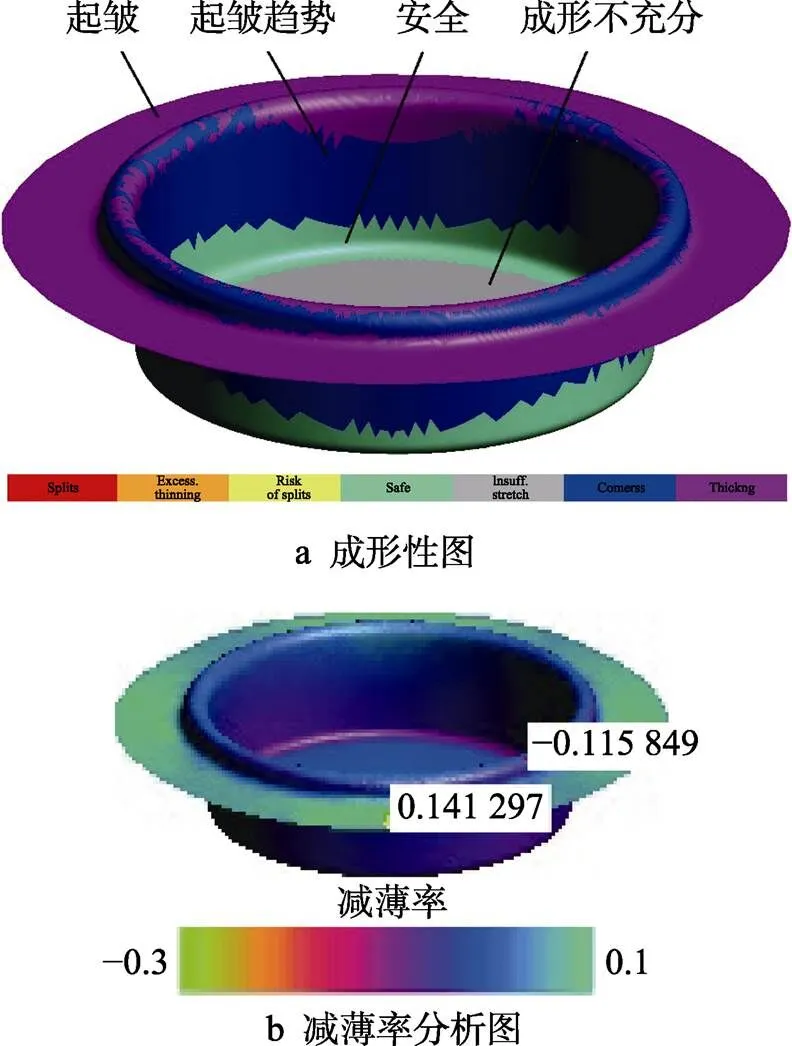
图5 初步工艺方案仿真结果

3 正交试验设计

3.1 试验因子与水平

影响拉延与反拉延成形的工艺参数众多，在确定料片材料与厚度后，以拉延摩擦因数1、反拉延摩擦因数2、拉延压边力1和反拉延压边力2（分别设为因子、因子、因子和因子）为研究对象，研究对圆筒形件多步冲压成形质量的影响。

考虑到冷轧钢板DC03的拉延摩擦因数、反拉延摩擦因数通常在0.10～0.20之间，因此，可将此范围作为1和2试验水平的设计依据；拉延压边力的确定通常是结合AutoForm软件仿真，视仿真情况，通过观察过程数据进行二次调整而获取[21]，因此，分别以45 kN和30 kN为中间值、以5 kN为公差来确定1和2具体的5组水平值。设计的正交试验因子及水平如表2所示。

表2 正交试验因子及水平

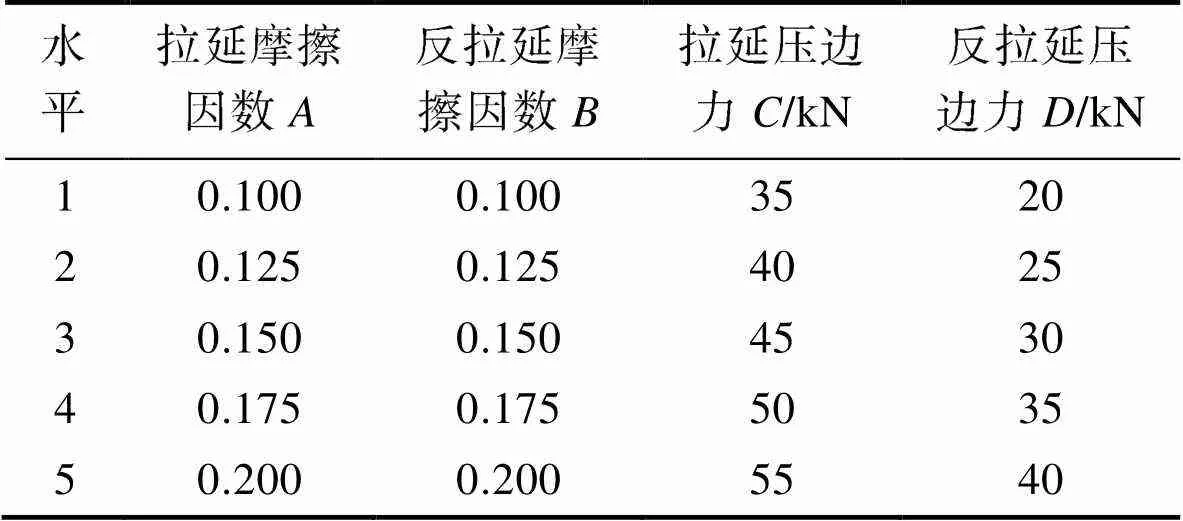
Tab.2 Orthogonal experiment factors and levels

3.2 正交试验方案

在制件未开裂和起皱的前提下，以减薄率极值（max、min）为正交试验的评价指标，采用极差分析法研究各因子对max、min的影响显著性。以1、2、1和2为4个因子、以减薄率极值为优化目标，设计的正交试验表L25(54)如表3所示。

3.3 正交试验结果分析

由表3可知，min在−0.11～−0.12之间，max在0.14～0.15之间，相较而言，在各因子的约束范围内，优化max对提高圆筒形件的成形质量效果更佳，故选择max作为圆筒形件质量的评价指标，且该值越小越好。由表3可知，第25组参数下的max最优、第5组参数下的max最劣，但该结果仅限于25组特定组合。通过极差分析法可以方便地比较max的优劣程度，以达到减少仿真试验次数的目的，表4为正交试验的极差分析数据。观察表4可知，各因子极差的大小为R>R>R>R，极差大小体现了各因子对结果的影响程度，极差越大，该因子对max的影响越显著，所以各因子对max影响的主次顺序为>>>，结合表4确定的相对最优工艺参数如下：拉延摩擦因数为0.200、反拉延摩擦因数为0.100、拉延压边力为50 kN、反拉延压边力为30 kN。以该参数组为仿真参数边界，得到仿真值max=0.144 4，该值仅次于表3中最优工艺参数组（第25组）的仿真值max。

表3 正交试验表L25(54)

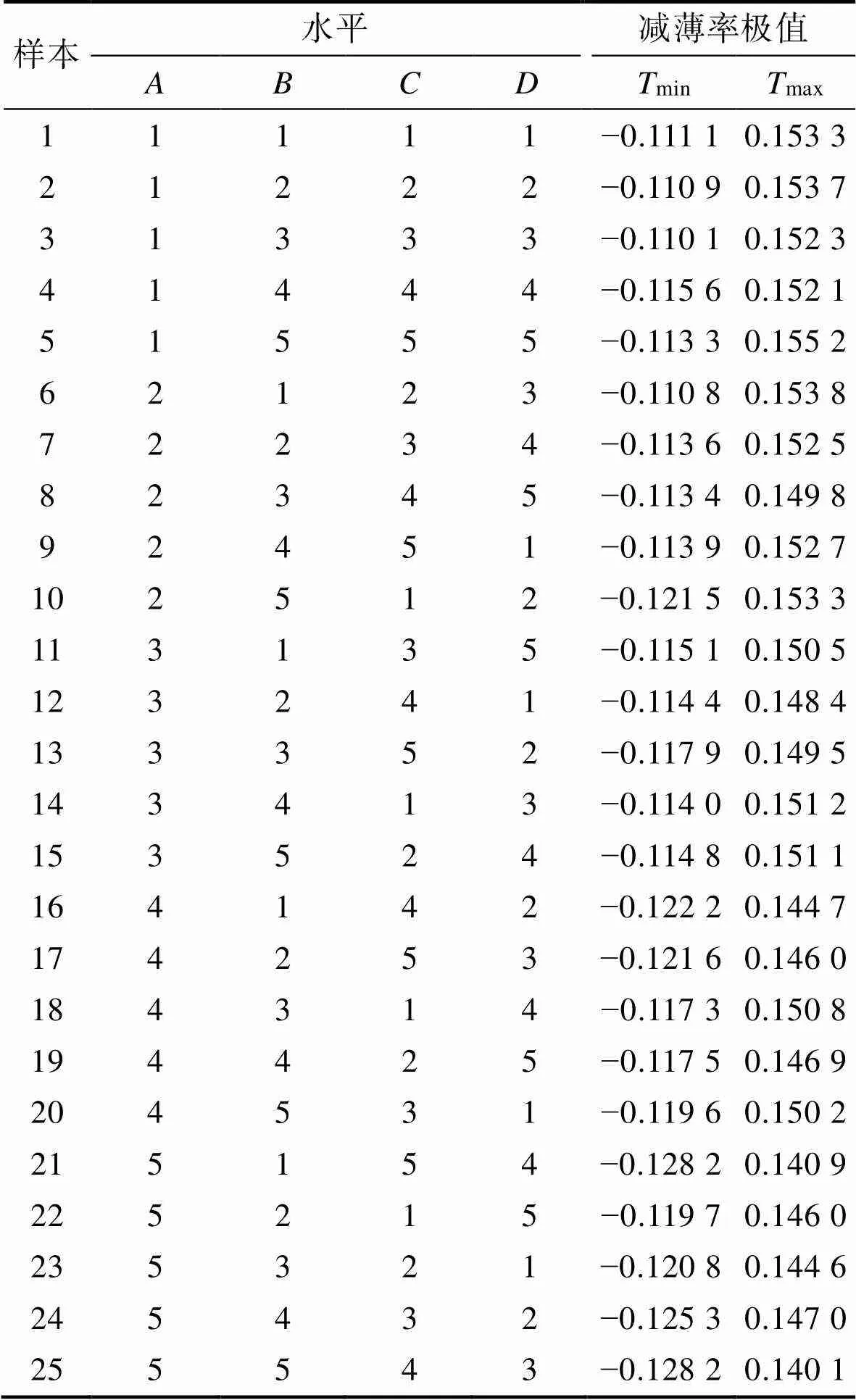
Tab.3 Orthogonal experiment L25(54)

表4 正交试验极差分析数据

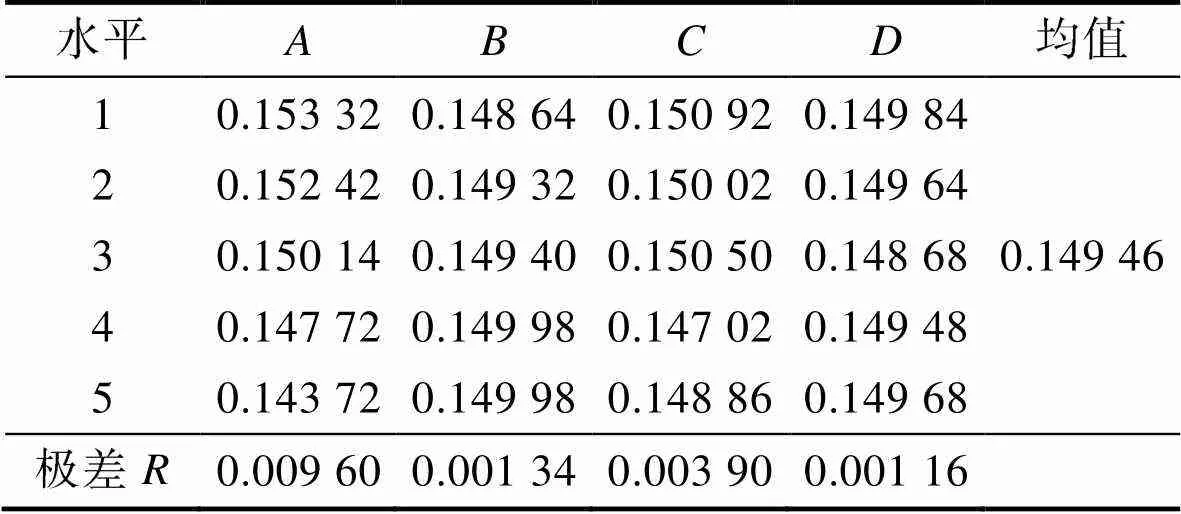
Tab.4 Range analysis data of orthogonal experiment

为直观地表达各因子对max的影响，应用表4数据绘制出各因子与max的关系，如图6所示。图中各因子折线纵坐标的极大高度差为极差。上述分析所获得的最优工艺参数仅限于表1初定的5个水平，该最优工艺参数下的仿真值只能代表54次全面试验中的最优值，可能不是各因子约束范围内的最优值。针对此不足，基于Matlab平台应用BP神经网络对正交表中各样本数据进行训练，建立BP神经网络模型以预测各因子在约束范围内所有组合的冲压结果，并通过遗传算法对BP神经网络模型进行工艺参数寻优，以获得各因子约束范围内的最优工艺参数。

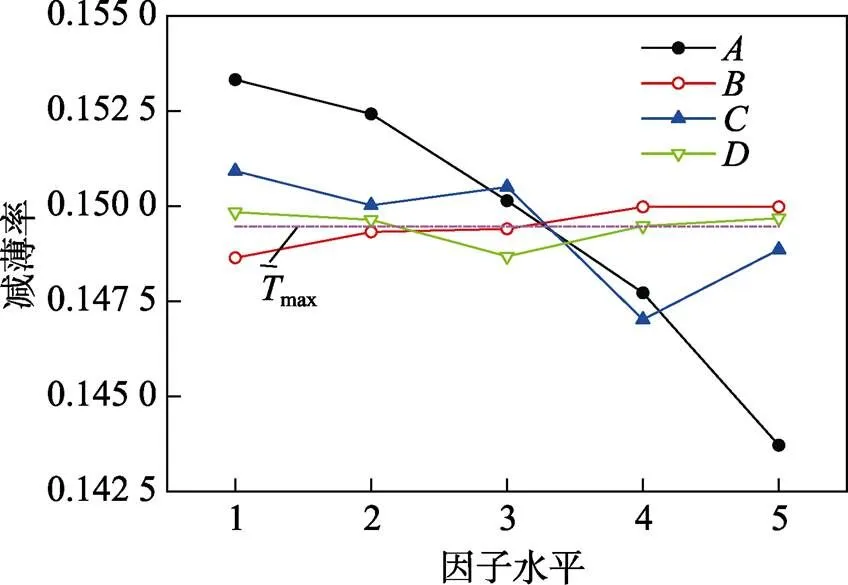
图6 各因子与Tmax的关系

4 工艺参数优化

4.1 BP神经网络预测

神经网络是由大量的神经元互相连接而构成的网络。目前神经网络的实际应用主要有前馈、反馈和自组织型3种，其中前馈神经网络及其变化形式最为常用，如BP神经网络。BP神经网络算法的主要思想如下：对于个输入学习样本1，2，…，，已知与其对应的个输出样本为1，2，…，，用网络的实际输出1，2，…，与目标矢量1，2，…，之间的误差来修改神经网络的权值，使（=1，2，…，）与期望的（=1，2，…，）尽可能接近，即使网络输出层的误差平方和达到最小。

Matlab仿真过程如下：（1）构建3层BP神经网络对max进行预测，输入层节点数为4，隐含层节点数为9，隐含层的激活函数为tansig，输出层节点数为1，输出层的激活函数为purelin；（2）采用梯度下降动量和自适应lr算法traingdx训练BP网络，目标误差为1×10−6，学习率为0.05，最大迭代次数为2×105。

取表2中25个输入学习样本与对应的输出样本max来训练样本数据，经过5 001次迭代，系统误差达到目标误差1.0×10−6。BP神经网络拟合的max曲线如图7所示。对正交试验方案之外的4组数据分别进行软件仿真与BP神经网络预测，以获得仿真值和预测值之间的相对误差，如表5所示。该相对误差在1%之内，故建立的BP网络模型是可靠的。

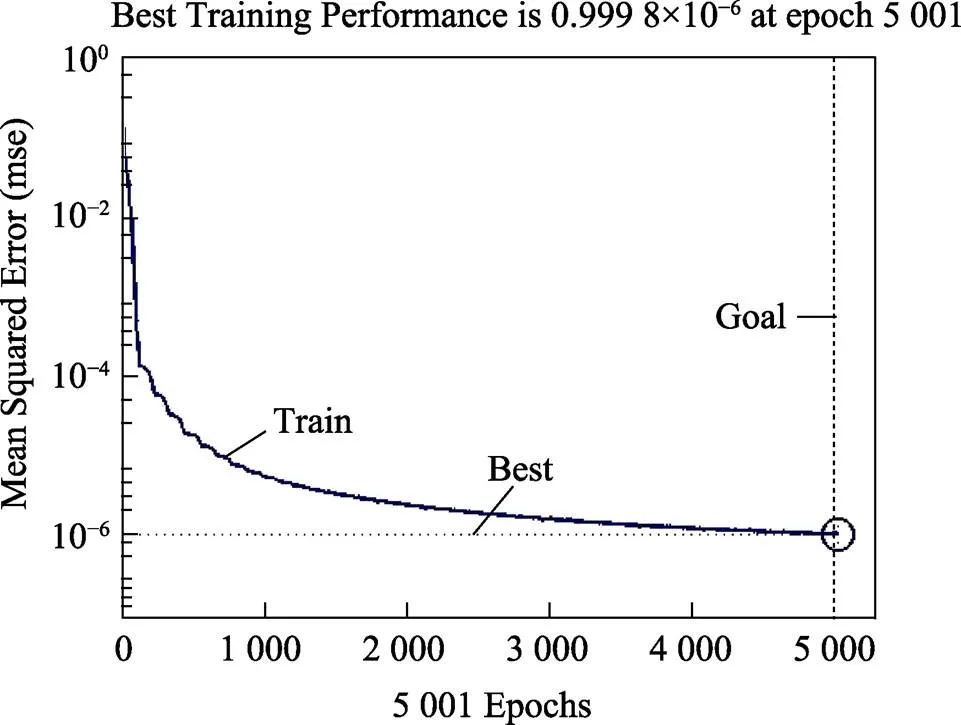
图7 BP神经网络拟合的Tmax曲线

表5 仿真值和预测值之间的相对误差

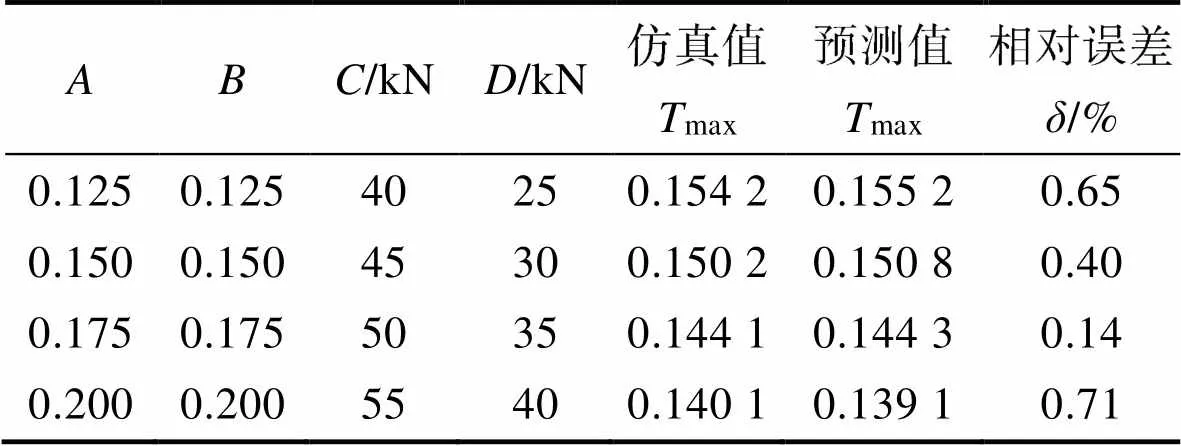
Tab.5 Relative error between simulated value and predicted value

4.2 遗传算法寻优

遗传算法是一种模拟生物在自然环境中的遗传和进化过程而形成的并行、高效、全局搜索的方法，它具有自组织、自适应和自学习等特点。文中以拉延摩擦因数、反拉延摩擦因数、拉延压边力和反拉延压边力为设计变量，各因子取值范围为表1中的水平1—水平5，选取max为优化目标，显然max越小越好。

Matlab仿真过程如下：（1）设置初始化种群数目为50，染色体进制编码长度为20，最大进化代数为100，交叉概率为0.7，变异概率为0.01；（2）产生初始种群，将二进制编码转换成十进制，计算个体适应度值，并进行归一化处理，采用操作、基于概率的交叉和变异操作，产生新的种群，并把历代最优个体保留在新种群中，进行下一步遗传操作；（3）判断是否满足终止条件，若满足，则结束搜索过程，输出优化值，若不满足，则继续进行迭代优化。

优化结束后，生成解的变化曲线和种群均值变化曲线，其适应度进化曲线如图8所示，得到最优工艺参数如下：拉延摩擦因数为0.200、反拉延摩擦因数为0.159、拉延压边力为55 kN、拉延压边力为40 kN。此时预测值max=0.134 9，该值比表3中最优工艺参数下的仿真值降低了3.71%，说明优化获得的工艺参数优于表3中的最优工艺参数。

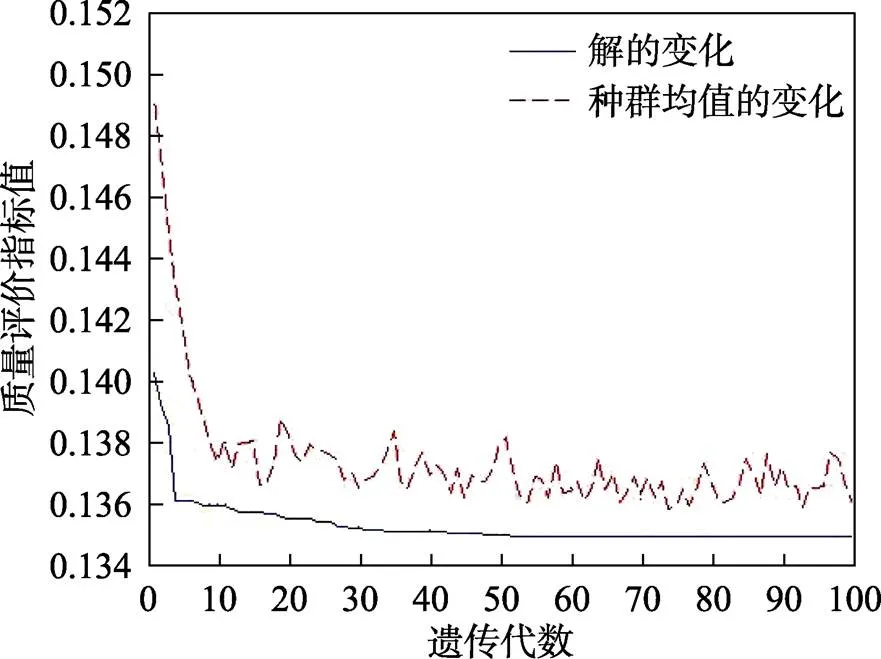
图8 适应度进化曲线

5 数值模拟验证

通过遗传算法对BP神经网络模型进行工艺参数寻优，应用各因子约束范围内的最优工艺参数进行仿真，得到max=0.140 1、min=−0.128 2，仿真结果如图9所示。可以看出，圆筒形件冲压成形质量良好，没有拉裂和起皱现象，不但应用最优工艺参数（拉延摩擦因数为0.200、反拉延摩擦因数为0.159、拉延压边力为55 kN、拉延压边力为40 kN）仿真获得的min比应用正交试验设计和极差分析所得的最优工艺参数对应的仿真值小，而且在同样对比条件下，max也略小，因此该制件成形质量最优。这进一步说明基于正交试验设计和极差分析方法、BP神经网络建模以及遗传算法寻优对制件的成形工艺进行量化调整是可行的。

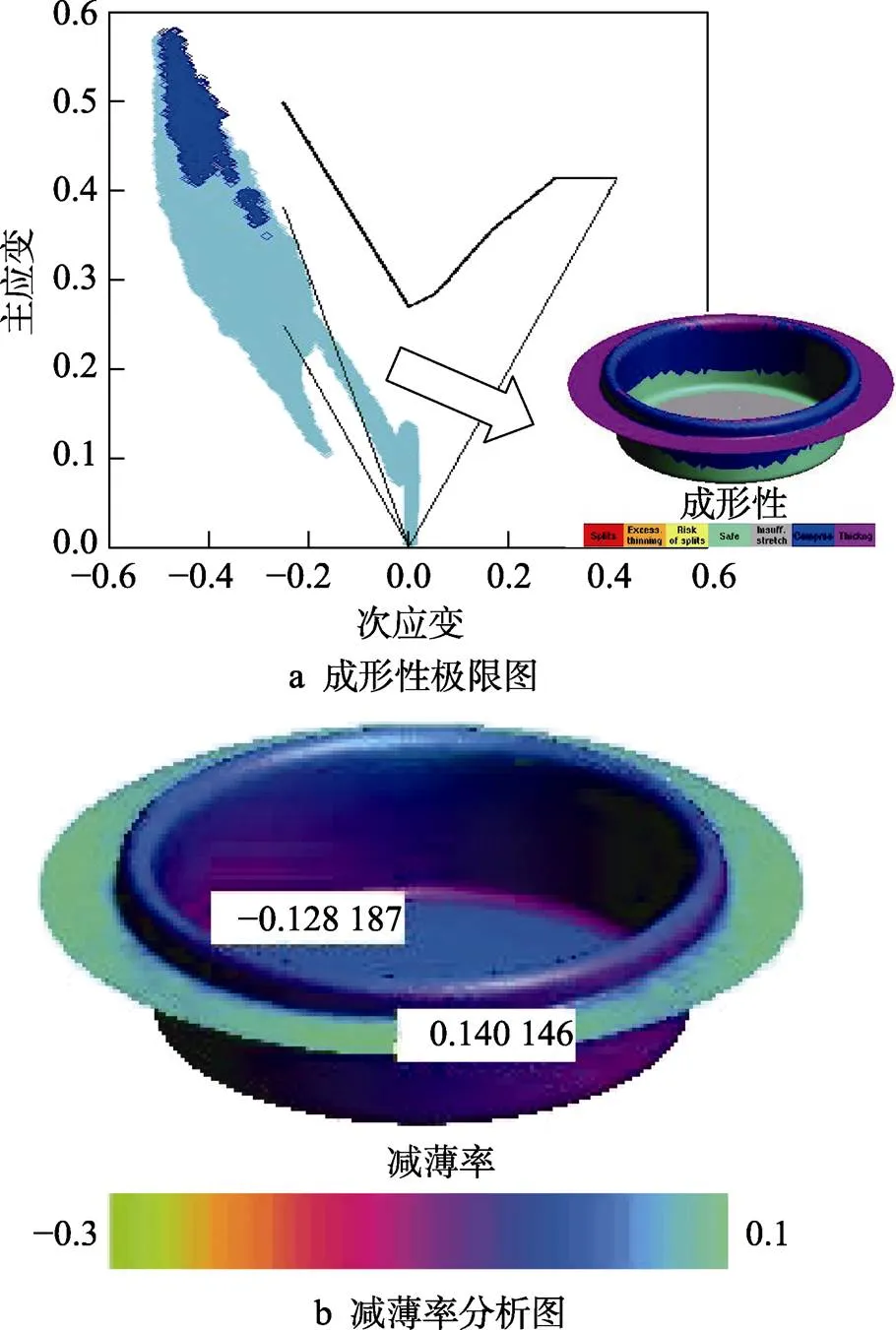
图9 遗传算法参数优化后板料数值模拟结果

6 结论

针对圆筒形件的成形特点结合工程经验提出了初步成形方案，获得了初步仿真结果。在制件未开裂和起皱的前提下，分析了正交试验L25(54)样本的优劣程度，以极大减薄率max为正交试验的评价指标，采用极差分析法分析了影响max的因素的主次关系，并获得了最优工艺参数。应用该参数进行仿真，得到的仿真值仅次于正交试验表中第25组工艺参数组的仿真值。

基于Matlab平台应用BP神经网络对正交表中各样本数据进行训练，建立了BP神经网络模型，预测了各因子在约束范围内所有组合的冲压结果，并进一步应用其他4组工艺参数下仿真值和预测值之间的相对误差验证了BP神经网络模型的准确性。在此前提下，通过遗传算法对BP神经网络模型进行工艺参数寻优，获得各因子约束范围内的最优工艺参数。应用该参数进行仿真得到的仿真值优于正交试验表中第25组最优工艺参数组的仿真值。

上述方案可为缩短级进模开发周期、降低生产成本、量化调整拉延工艺参数提供一定指导，具有较好的工程应用价值。

[1] 李钦生, 江丙云. 多道次深拉延工艺数值模拟与实验比较研究[J]. 制造技术与机床, 2019(6): 180-183.

LI Qin-sheng, JIANG Bing-yun. The Comparative Study on Numerical Simulation&Experiment in Multi-Step DeepDrawing[J]. Manufacturing Technology & Machine Tool, 2019(6): 180-183.

[2] 陈楠, 李永华. 汽车右门拉延工艺的数值模拟[J]. 沈阳理工大学学报, 2019, 38(6): 43-46.

CHEN Nan, LI Yong-hua. Numerical Simulation of the Deep Drawing Process for Auto Right Door[J]. Transactions of Shenyang Ligong University, 2019, 38(6): 43-46.

[3] 马春燕. 轻卡顶盖外板冲压工艺分析与模具设计研究[D]. 济南: 山东大学, 2019: 1-5.

MA Chun-yan. Stamping Process Analysis and Die Design of Light Truck Top Cover Outer Plate[D]. Jinan: Shandong University, 2019: 1-5.

[4] 包子阳, 余继周. 智能优化算法及其MATLAB实例[M]. 北京: 电子工业出版社, 2017: 1-6.

BAO Zi-yang, YU Ji-zhou. Intelligent Optimization Algorithm and Its MATLAB Example[M]. Beijing: Machinery Industry Press, 2017: 1-6.

[5] 蔡自兴, 王勇. 智能系统原理、算法与应用[M]. 北京: 机械工业出版社, 2014: 2-19.

CAI Zi-xing, WANG Yong. Principle, Algorithm and Application of Intelligent System[M]. Beijing: Machinery Industry Press, 2014: 2-19.

[6] 温正. 精通MATLAB智能算法[M]. 北京: 清华大学出版社, 2015: 15-30.

WEN Zheng. Proficient in MATLAB Intelligent Algorithm [M]. Beijing: Tsinghua University Press, 2015: 15-30.

[7] 胡锦达. 汽车后围内板冲压工艺的高斯扰动粒子群优化[J]. 锻压技术, 2020, 45(12): 46-52.

HU Jin-da. Stamping Process Optimization of Automobile Rear Inner Panel Based on Gaussian Perturbation Particle Swarm[J]. Forging & Stamping Technology, 2020, 45(12): 46-52.

[8] 郭强, 郑燕萍, 朱伟庆, 等. 基于BP神经网络遗传算法的高强钢成形研究[J]. 材料科学与工艺, 2020, 28(2): 89-96.

GUO Qiang, ZHENG Yan-ping, ZHU Wei-qing, et al. Research on High Strength Steel Forming Based on BP Neural Network Genetic Algorithms[J]. Materials Science and Technology, 2020, 28(2): 89-96.

[9] 谢延敏, 唐维, 黄仁勇, 等. 基于SA-RBF神经网络的冲压成形拉延筋优化[J]. 西南交通大学学报, 2017, 52(5): 970-976.

XIE Yan-min, TANG Wei, HUANG Ren-yong, et al. Drawbead Optimisation in Stamping Using SA-RBF Neural Networks[J]. Journal of Southwest Jiaotong University, 2017, 52(5): 970-976.

[10] 王新宝, 谢延敏, 王杰, 等. 基于改进PSO-BP的拉延筋参数反求优化[J]. 锻压技术, 2014, 39(4): 10-15.

WANG Xin-bao, XIE Yan-min, WANG Jie, et al. Parameter Inverse Optimization for Drawbeads Based on Improved PSO-BP Model[J]. Forging & Stamping Technology, 2014, 39(4): 10-15.

[11] 邱超斌, 张猛, 郎利辉, 等. 基于神经网络遗传算法的深腔型零件拉深工艺参数优化[J]. 精密成形工程, 2021, 13(5): 173-179.

QIU Chao-bin, ZHANG Meng, LANG Li-hui, et al. Parameter Optimization of Deep Drawing Process for Deep Cavity PartsBased on Neural Network Genetic Algorithm[J]. Journal of Netshape Forming Engineering, 2021, 13(5): 173-179.

[12] 王泌宝. 汽车B柱加强板热冲压工艺的遗传算法多目标优化[J]. 锻压技术, 2021, 46(5): 46-52.

WANG Mi-bao. Multi-Objective Optimization on Hot Stamping Process for Vehicle B-Pillar Reinforced Plate Based on Genetic Algorithm[J]. Forging & Stamping Technology, 2021, 46(5): 46-52.

[13] 李雷, 赵柏森. 基于人工神经网络和遗传算法的封头成形工艺参数多目标优化[J]. 锻压技术, 2021, 46(5): 39-45.

LI Lei, ZHAO Bai-sen. Multi-Objective Optimization on Head Forming Process Parameters Based on Artificial Neural Network and Genetic Algorithm[J]. Forging & Stamping Technology, 2021, 46(5): 39-45.

[14] 黄昭明, 赵恒文, 刘小飞, 等. 筒形件多次拉延与反拉延成形仿真与优化[J]. 南京工程学院学报, 2018, 16(1): 44-48.

HUANG Zhao-ming, ZHAO Heng-wen, LIU Xiao-fei, et al. Simiulation and Optimization for Multiple Drawing and Insind-out Redrawing of Cylindrical Parts[J]. Joumal of Nanjing Institute of Technology, 2018, 16(1): 44-48.

[15] 吴向东, 张毅升, 万敏, 等. 板材成形性能试验方法及应用[J]. 精密成形工程, 2019, 11(3): 42-50.

WU Xiang-dong, ZHANG Yi-sheng, WAN Min, et al. Application and Test Methods of Sheet Metal Formability [J]. Journal of Netshape Forming Engineering, 2019, 11(3): 42-50.

[16] 王利, 黄昭明, 赵恒文, 等. 多弯曲多形孔复杂边界钣金件级进模的开发[J]. 延边大学学报, 2020, 46(1): 74-78.

WANG Li, HUANG Zhao-ming, ZHAO Heng-wen, et al. Development of Progressive die for Complex Boundary Sheet Metal Parts with Multi Bend and Multi Hole Features[J]. Journal of Yanbian University, 2020, 46(1): 74-78.

[17] 赵殿明, 黄昭明, 王利, 等. 发动机油底壳自动线多工位传递模设计与应用[J]. 锻压技术, 2019(8): 137-142.

ZHAO Dian-ming, HUANG Zhao-ming, WANG Li, et al. Design and Application of Automatic Line Multi-Station Transfer Die for Engine Oil Pan[J]. Forging & Stamping Technology, 2019, 44(8): 137-142.

[18] 赵殿明, 黄昭明, 陈华, 等. 多弯角车身钣金件多工位级进模设计与应用[J]. 锻压技术, 2020, 45(3): 125-130.

ZHAO Dian-ming, HUANG Zhao-ming, CHEN Hua, et al. Design and Application of Multi-Position Progressive Die for Multi-Angle Car Body Sheet Metal Parts[J]. Forging & Stamping Technology, 2020, 45(3): 125-130.

[19] 罗志敏. 轿车前纵梁冲压成形工艺多目标优化及模具技术研究[D]. 长沙: 湖南大学, 2012: 30-31.

LUO Zhi-min. Stuy on Multi-Objective Optimization of Forming Process of Front Rail and Die Techology[D]. Changsha: Hunan University, 2012: 30-31.

[20] 焦欣, 吴越武. 基于正交试验的工艺参数对门内板成形性的影响[J]. 塑性工程学报, 2020, 27(12): 73-81.

JIAO Xin, WU Yue-wu. Influence of Process Parameters on Formability of Door Inner Panel Based on Orthogonal Test[J]. Journal of Plasticity Engineering, 2020, 27(12): 73-81.

[21] 涂小文. AutoForm原理技巧与战例使用手册[M]. 武汉: 湖北科学技术出版社, 2013: 419-423.

TU Xiao-wen. Principle Skills and Examples of AutoForm[M]. Wuhan: Hubei Science and Technology Press, 2013: 419-423.

Optimization of Multi-step Stamping Process Parameters of Cylindrical Parts Based on GA-BPNN

BAI Yue-xiang1,2, HUANG Zhao-ming2,3,WANG Li2, ZHANG Yong-ming1, SHEN Chen2,3

(1. School of Mechanical and Electrical Engineering, Jiangxi Vocational and Technical College of Communications, Nanchang 330013, China; 2. Maanshan Engineering Technology Research Center for Advanced Design of Automobile Stamping Die, Anhui Maanshan 243031, China; 3. Technology Department of Wuxi Jiuhe Mould Co., Ltd., Jiangsu Wuxi 214142, China)

The work aims to study the formability of cylindrical parts in precision multi-step stamping. Aiming at the formability problems in multi-step stamping of cylindrical parts, the optimal process parameters were obtained based on orthogonal experimental design, range analysis method, BP neural network modeling and genetic algorithm, and the effect of relevant process parameters on the thinning rate in the forming process was studied. Through orthogonal experimental design and range analysis, the primary and secondary order of the effect of each parameter on the maximum thinning rate was drawn friction factor > drawn blank holder force > reverse drawn friction factor > reverse drawn blank holder force. The relative optimal process parameters were as follows: the drawn friction factor was 0.200, the reverse drawn friction factor was 0.100, the drawn blank holder force was 50 kN, and the reverse drawn blank holder force was 30 kN. The extreme simulation value of the maximum thinning rate was 0.144 4 and the extreme simulation value of the minimum thinning rate was −0.127 7. Taking the maximum thinning rate as the forming quality evaluation index, through BP neural network modeling and genetic algorithm optimization, the optimal process parameters were obtained as follows: the drawn friction factor was 0.200, the reverse drawn friction factor was 0.159, the drawn blank holder force was 55 kN, and the drawn blank holder force was 40 kN. The relative error between the predicted value of the maximum thinning rate (0.134 9) and the simulation value (0.140 1) was only 3.7%, and the forming quality of the parts after optimization was good. The proposed method has good engineering application value for quantificationally adjusting the forming process of parts.

orthogonal experimental; BP neural network; genetic algorithm; process parameters; thinning rate

10.3969/j.issn.1674-6457.2022.09.011

TG386.1

A

1674-6457(2022)09-0079-07

2021–09–30

江西省教育厅科学技术研究项目（204606）；马鞍山工程技术研究中心开放基金（QMSG202102，QMSG202104）

白月香（1979—），女，硕士，副教授，主要研究方向为金属板料成形工艺与模具设计。

黄昭明（1981—），男，博士，副教授，主要研究方向为金属板料成形工艺与模具设计。

责任编辑：蒋红晨