汽车转向节臂端部冷精整工艺优化

宛加雄，武建祥，晏洋，丁华锋,

汽车转向节臂端部冷精整工艺优化

宛加雄1，武建祥2，晏洋2，丁华锋1,2

（1.纯电动汽车电力系统设计与测试湖北省重点实验室，湖北 襄阳 441053；2.湖北三环锻造有限公司，湖北 襄阳 441700）

得到单向压缩冷精整的精整量与预变形孔半径和深度之间的变化规律，以及摩擦因数大小同回弹量之间的关系。对转向节臂端部锻件上下表面进行预变形凹槽孔处理，并建立锻件单向压缩冷精整的弹塑性有限元模型，利用ABAQUS有限元软件进行数值模拟仿真，分析摩擦因数对表面质量的影响，得到优化后的工艺参数，并进行实验验证模拟结果的准确性。摩擦因数越大，冷精整后的转向节臂端部锻件的鼓形越明显。在精整量为1 mm的情况下，当预变形凹槽孔的半径为4 mm、深度为0.3 mm、单向压缩量为1.1 mm、摩擦因数为0.2时，能够得到最好的表面质量。当摩擦因数相同时，预变形凹槽孔的半径越大，径向位移越小，而回弹量基本保持不变。

汽车转向节臂；冷精整；工艺优化；回弹量

转向节臂在汽车行驶过程中起重要作用，是汽车上重要的安保件，其几何精度直接影响装配效果。随着有限元技术的发展，学者们利用CAE软件进行了大量研究[1-5]。章志兵等[6]基于CAE模型船舶舱室的相关研究，提出了一种半封闭空间的新概念，并设计了全船CAE模型的识别算法，实现了半面扩展算法的高效性和准确性。刘江等[7]针对转向节在实际生产过程中出现的塌角等缺陷问题，通过数值模拟和实验验证提出了复合成形工艺，使材料利用率达到了80.8%，成品合格率达到了97.9%。赵毅等[8]分析了某皮卡的转向节热锻成形过程，采用大小台阶式阻力模具设计方法，解决了锻件填充不满的问题。在实际生产中，通常采用冷精压的方法来提高转向节臂端部的几何精度。王德林等[9]分析了三销轴叉冷精整工艺过程中型腔底部应力、应变的变化情况，优化设计了不同的入模角，使冷精整后的型腔底部范围区域没有产生裂纹，显著提高了冷精整锻件的产品质量。Stone等[10]通过ABAQUS软件建立了厚壁圆筒的有限元模型，研究了精整量对表面质量的影响，结果表明，冷精整能够改善工件的表面质量且不会对工件外部形状产生影响。朱怀沈等[11]研究了冷精整工艺过程中直齿轮的齿面冷精整量与齿面之间回弹量的变化关系，得到了精整量与壁厚之间的优化选择。郭嘉晨等[12]用Kriging模型和粒子群算法改善了冷精整工艺中万向节滑套杯壁的表面质量。Kwanghyun等[13]整合了欧拉光束理论并预测了螺旋管蒸汽发生器的弯曲回弹情况，将流变应力和弹性模量的数值应用到分析模型当中，精确预测了最终尺寸。Farhad等[14]建立了非线性运动模型，发现改变载荷的顺序能够明显减小弯曲回弹角。Soheil等[15]和Uten等[16]研究发现，锻造时，在低摩擦条件、不考虑折叠的情况下，当最大摩擦因数≤0.5时，Avitzur模型具有最高的准确性。Fras等[17]研究发现，高载荷下表面之间的直接接触会导致摩擦力显著增加，对工件会造成不可预估的缺陷。在实际的冷精整过程中，压头与工件表面存在摩擦，这会导致工件的精整表面粗糙，而摩擦因数的大小对精整表面的影响很大。

目前针对汽车转向节臂冷精整工艺优化的研究还比较少，上述研究忽略了摩擦因数对表面质量的影响。文中采用在转向节臂端部上下表面设置预变形凹槽的方法来提高表面质量，将压缩量作为关键参数，对转向节臂端部圆棒进行单向压缩冷精整加工，通过ABAQUS有限元仿真软件分析孔的半径和深度对回弹量的影响，同时研究摩擦因数对表面质量的影响规律，表面质量通过冷精整回弹后转向节臂端部上表面节点的轴向位移表现。

1 转向节臂端部冷精压工艺

1.1 转向节臂结构

转向节臂锻件图如图1所示。转向节臂是汽车转向系统的最后一级传力部件，转向节臂一端安装在上下转向节之间，另外一端则用球销与横拉杆连接。因此端部的表面质量将直接影响转向节臂的力学性能。

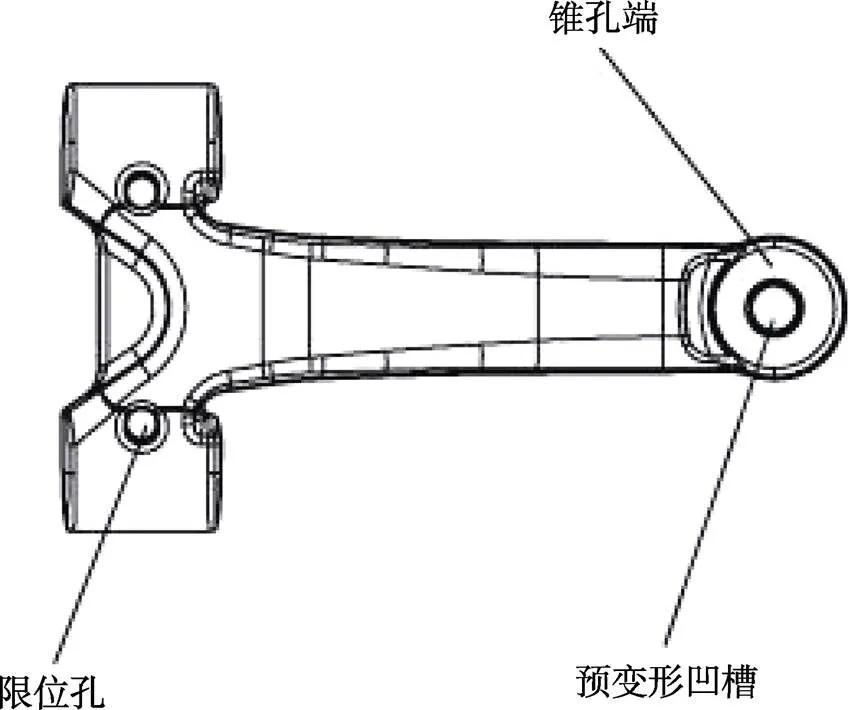
图1 转向节臂锻件图

1.2 塑性应变和摩擦影响

对锻件进行单向压缩，由于外端表面受摩擦力的影响，变形难度增加，因此会发生凸缘现象。单向压缩的初始和最终形状如图2所示，得到的曲率半径表达式如式（1）所示。

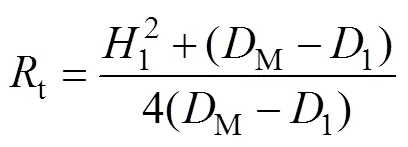
式中：H1为最终高度；DM为最大直径；D1为顶部直径。

摩擦因数的测定对塑性成形至关重要[18-21]。在转向节臂端部单向压缩冷精整过程中，当不考虑摩擦条件时，冷精整为理想单向压缩模型，此时转向节臂端部轴向尺寸变化相同。随着摩擦因数的增大，接触面外端变形困难，使上下接触表面变形小于中间部分的变形，进而产生鼓形。随着摩擦因数的进一步增大，鼓形越加明显。下面将通过有限元数值模拟得到摩擦因数大小对转向节臂回弹量的定量影响规律。

2 冷精压有限元仿真

在转向节臂端部冷精压过程中，在摩擦力的影响下，精整表面质量较为粗糙。为得到冷精整时的变形规律及较高的表面质量，在转向节臂端部先加工一个预变形凹槽孔，研究预变形凹槽孔的开口大小、深度以及表面摩擦因数对回弹量的影响，以实现冷精整量的优化选择。文中转向节臂端部外径为57 mm，轴向长度为35 mm，冷精整后的轴向长度为34 mm，端部外圆直径增大不超过1%。设计预变形凹槽孔的半径为2、3、4 mm，深度为0.5、0.3 mm，研究摩擦因数分别为0、0.1、0.2、0.3、0.4时转向节臂端部的回弹大小。文献[22]表明，摩擦因数通常小于0.4，因此文中的摩擦因数最大取值为0.4。

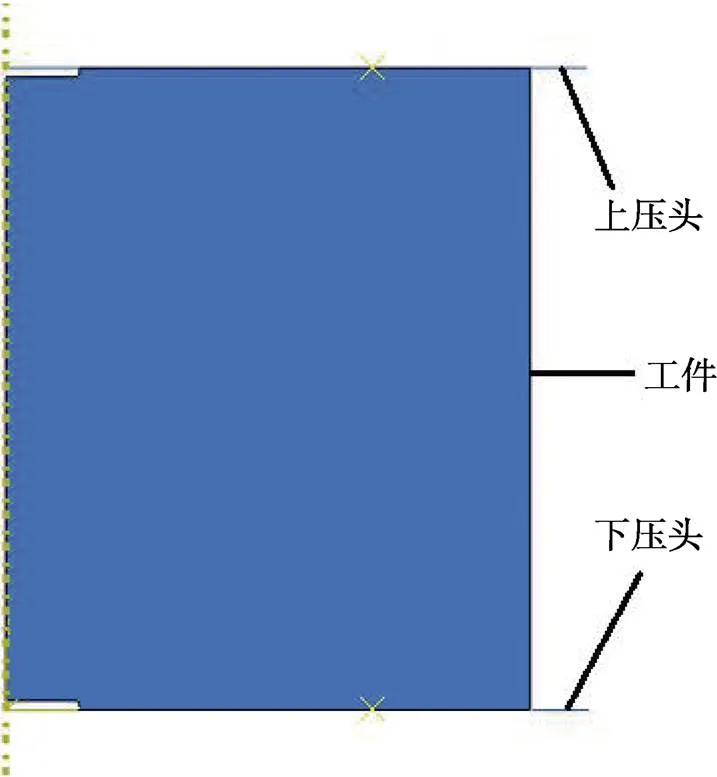
图3 转向节臂端部精整模型

2.1 弹塑性有限元精整模型的建立

在冷精整成形过程中，转向节臂的内部发生了弹塑性变形，积攒了弹性势能，当卸除载荷后，弹性势能释放从而发生回弹，因此用弹塑性模型分析。材料为42CrMo高强度合金钢，其屈服强度为930 MPa、抗拉强度为1 080 MPa、密度为7.85 g/cm3、弹性模量为2.02×105MPa、泊松比为0.28，材料为均质且各向同性，在整个过程中不计算体积力与惯性力，遵循米塞斯屈服准则。由于转向节臂端部的圆柱体是轴对称零件，因此在模拟时选择二维坯料，只分析1/2模型以减少计算量[23-25]，再对中间预变形凹槽孔进行局部网格的细化处理。冷精整开始前先设置一步静接触，使接触关系平稳建立，并设置不同的摩擦因数来进行对比分析。

在冷精整过程中，金属一部分沿径向方向向内流动，填充预变形凹槽孔，另一部分沿着径向方向向外流动，使径向尺寸增大。转向节臂端部精整过程位移场分布情况如图4所示，其内部金属组织以轴向方向流动为主，以径向方向流动为辅。

2.2 工艺参数的影响规律研究

为控制转向节臂端部冷精整的尺寸精度，研究转向节臂端部的回弹规律。根据仿真分析结果，得到不同预变形孔的大小和深度，以及在表面摩擦因数不同的条件下，单向压缩冷精整后径向位移1和轴向位移2的回弹量数据。

转向节臂端部预变形凹槽孔半径为0.5 mm和0.3 mm时，不同半径下的回弹量大小分别见图5和图6。根据回弹量数据可知，当预变形凹槽孔的半径相同时，预变形凹槽孔深度的影响可以忽略不计，径向位移和回弹量相等。在单向压缩精整过程中，由于精整量为1 mm，深度对转向节臂回弹量影响较小，仿真模拟预变形孔深度最小为0.3 mm，预变形凹槽孔能够有效提高精整后转向节臂端部上下表面质量。预变形凹槽孔的半径越大，径向位移越小，而回弹量基本不变。当摩擦因数为0.2时，径向位移的回弹量最大。摩擦因数越大，径向位移也就越大。因此，由数据对比得出，在半径为4 mm、深度为0.3 mm时，径向位移1和轴向位移2的综合效果最好。

图4 转向节臂端部精整过程位移场分布图

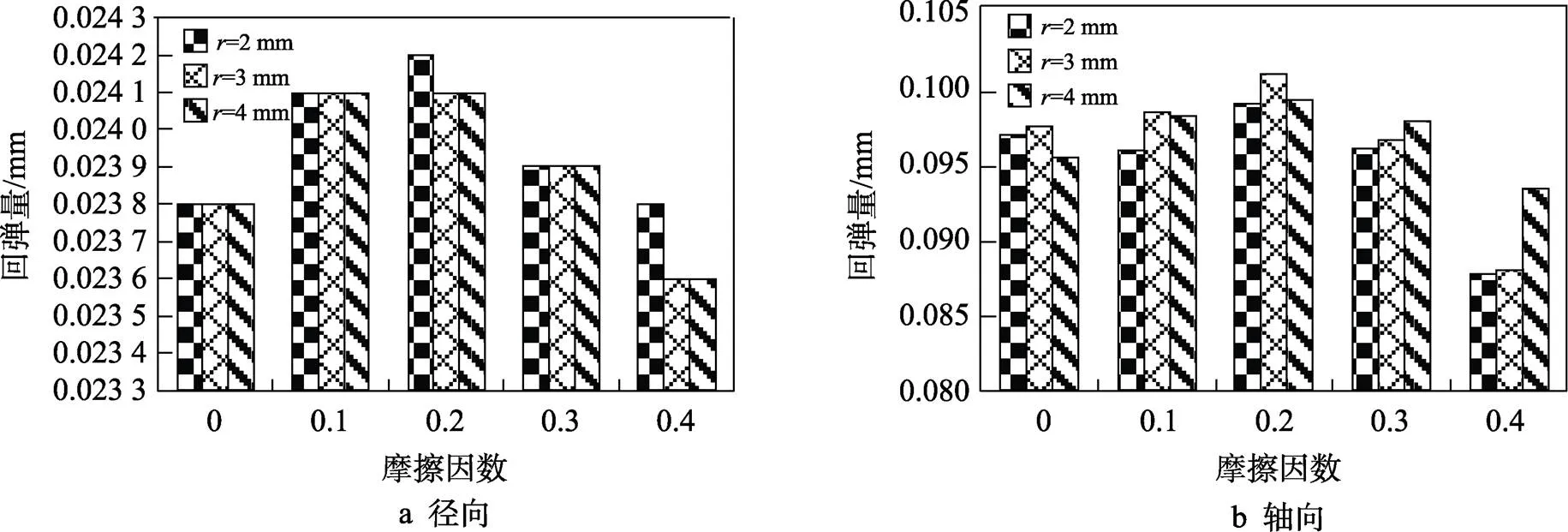
图5 预变形孔深度为0.5 mm时的回弹量

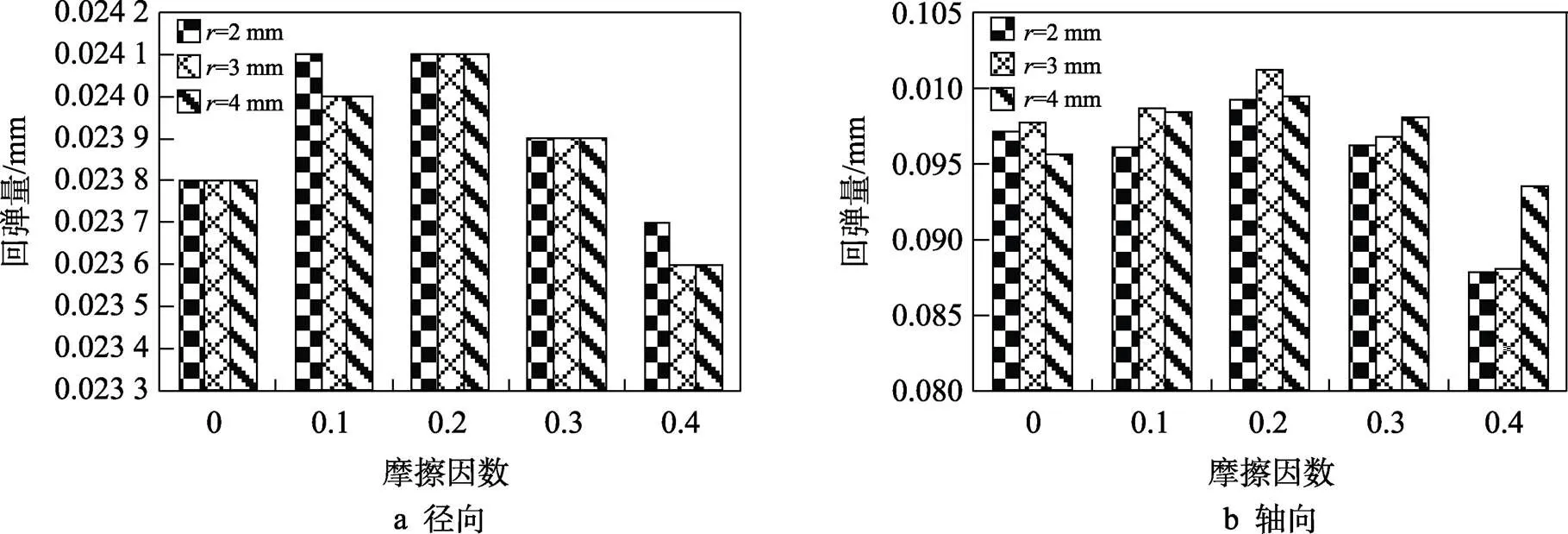
图6 预变形孔深度为0.3 mm时的回弹量

在相同的精整量下，随着摩擦因数的增大，上下表面变形困难，弹塑性变形过程中的弹性变形量先增大后减小，因而相应的回弹量也就呈先增大后减小的变化趋势。在深度为0.3 mm的精整条件下，3种不同半径大小的预变形凹槽孔在摩擦因数为0～0.4时的径向回弹量和轴向回弹量分别见图7和图8。由图7和图8可知，回弹量随着摩擦因数的增大，总体呈现先增大后减小的趋势，当摩擦因数为0.2时，回弹量最大。通过对比3种不同预变形凹槽孔半径的大小，得到在预变形凹槽孔半径为4 mm时，摩擦因数对回弹量影响最小。

考虑到摩擦对表面粗糙度的影响，仿真精整过程中上表面的轴向位移随时间的变化情况如图9所示。由图9可以看出，在前1 s的时间内，压头与转向节臂端部平稳接触，为降低速度对其产生的影响，将压缩精整的过程控制在3 s内，随后卸载压头，出现了回弹现象。

当精整量为1 mm时，压力卸载后出现了回弹现象，由于摩擦的影响，回弹结束后转向节端部上表面的位移并没有重合。为了准确地控制回弹量，将精整量确定为1.1 mm，预变形凹槽孔的深度为0.3 mm，得到的表面节点的轴向位移如图10所示。

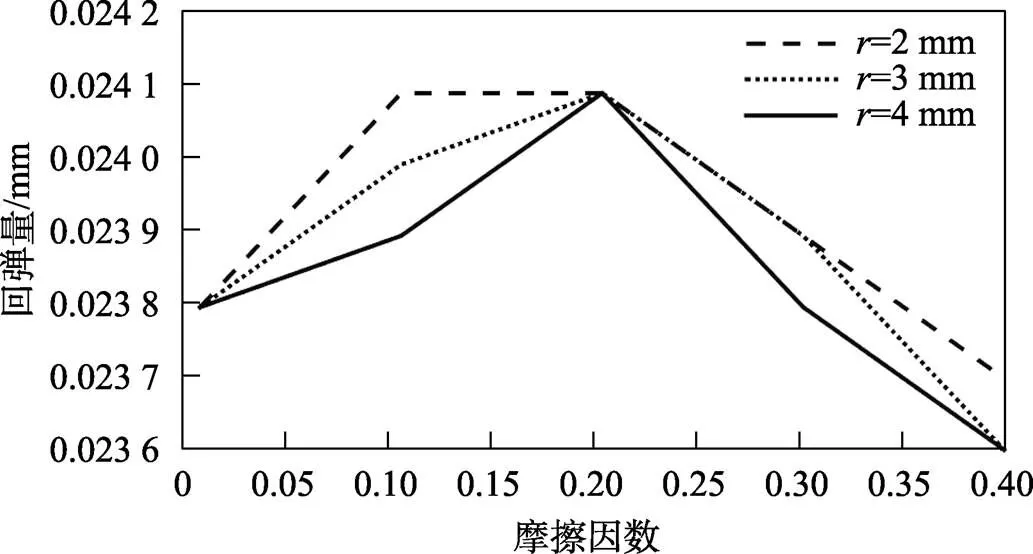
图7 不同摩擦因数下的径向回弹量

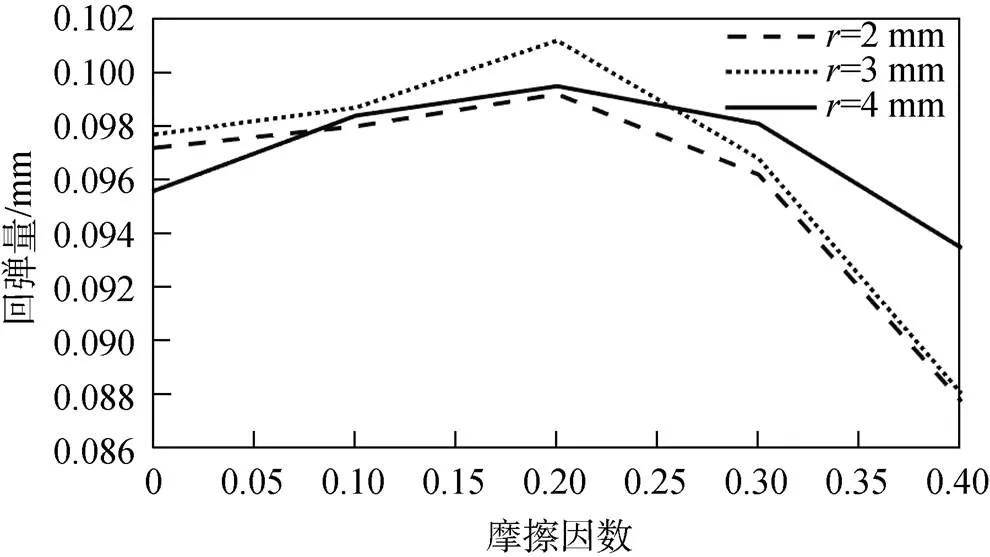
图8 不同摩擦因数下的轴向回弹量

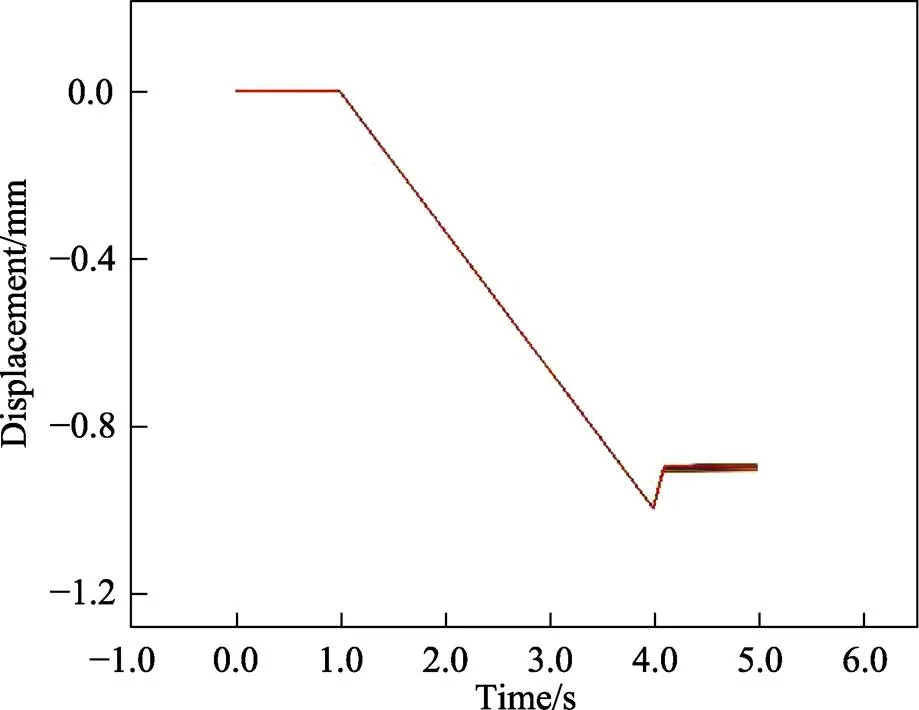
图9 精整过程中轴向位移随时间变化图形

图10是摩擦因数不同时，转向节臂端部圆棒上表面轴向位移值。由图10可知，在摩擦因数为0的理想状态下，整个上表面位移近似相同。当摩擦因数为0.2时，得到的位移值最接近1 mm。当摩擦因数不同时，转向节臂端部圆棒径向位移值如图11所示，根据图11可知，随着摩擦因数的增大，转向节臂端部在中间位置的位移增大，当摩擦因数为0时则不会产生鼓形，随着摩擦因数的增大，出现的鼓形越明显。由于摩擦的存在，转向节臂端部圆棒的上下表面与压头接触之间的摩擦切应力会导致靠近上下表面的位移很小。

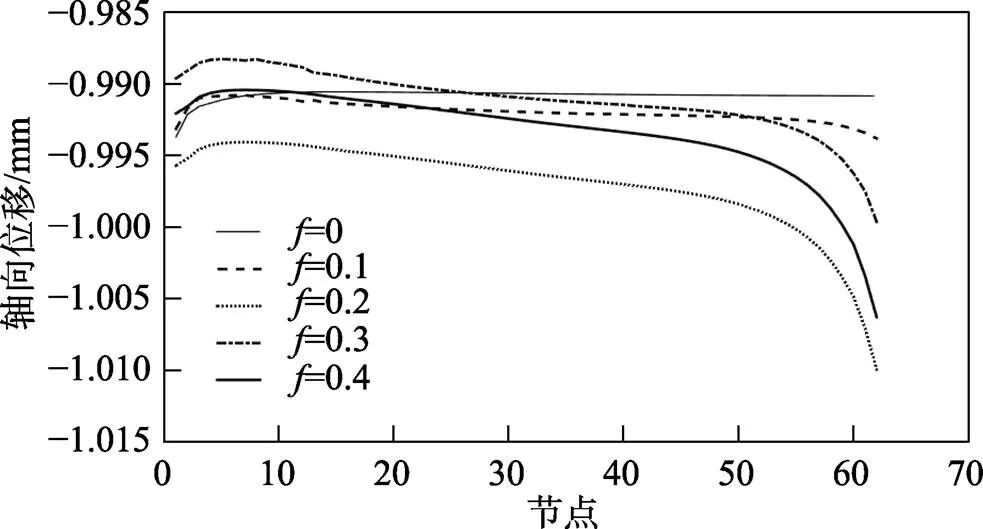
图10 转向节臂端部圆棒上表面轴向位移

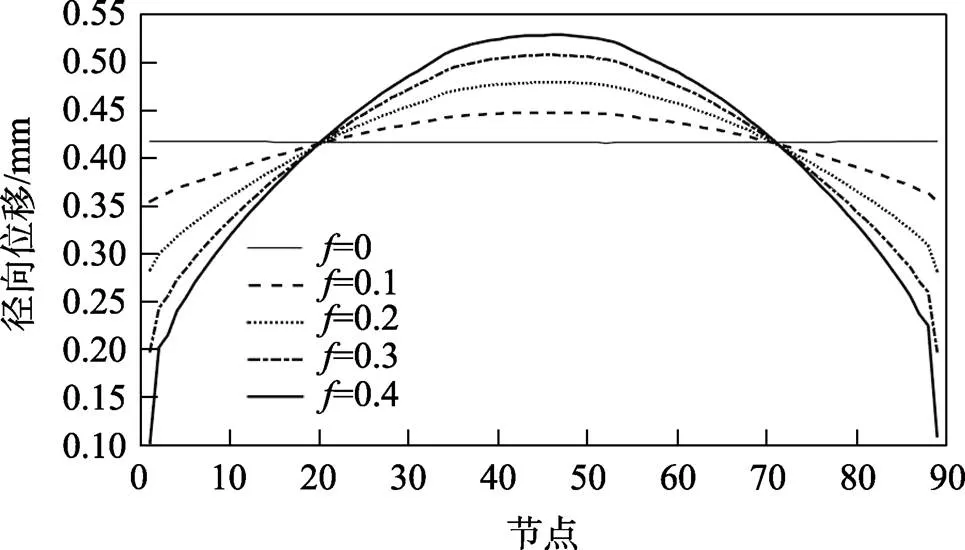
图11 转向节臂端部圆棒径向位移

3 实验结果验证

对转向节臂零件进行实物实验，以验证上述的仿真结果。首先在转向节臂的端部两端加工预变形凹槽孔，然后沿着厚度的方向对转向节臂端部进行冷精整，在冷精整过程中金属沿着端部外圆和预变形凹槽孔内径的方向流动，最后得到的汽车转向节臂如图12所示，测量其端部尺寸。

图12 冷精整后的转向节臂

考虑到实验成本，为减少实验时间，根据上述的模拟值，确定转向节臂端部预变形凹槽孔的半径为4 mm、深度为0.3 mm，对多个转向节臂试件进行实验，得到的实验测量数据如下：径向回弹量的模拟值为0.024 mm，测量值为0.023 1 mm，相对误差为3.8%；轴向回弹量的模拟值为0.096 3 mm，测量值为0.098 4 mm，相对误差为2.2%。由此能够看出，转向节臂的回弹测量值与实验模拟值的相对误差皆不超过5%，加工预变形凹槽孔能够有效保证转向节臂端部的表面质量，通过实验验证了模拟结果的准确性，实验的结果能够指导实际工业生产。

4 结论

通过弹塑性有限元分析，得到了摩擦因数与回弹量之间的变化关系以及预变形孔的大小对回弹的影响规律。

1）当摩擦因数相同时，预变形凹槽孔的半径越大，径向位移越小，而回弹量基本保持不变。在冷精整过程中，当预变形凹槽孔的半径相同时，预变形孔的深度影响可以忽略不计。

2）当摩擦因数为0.2时，径向位移的回弹量最大。随着摩擦因数的增大，转向节臂端部锻件鼓形越明显。

3）当预变形凹槽孔的半径为4 mm、深度为0.3 mm、摩擦因数为0.2时，转向节臂端部锻件的冷精整达到了工艺要求。基于所得到的结论，可以对精整量进行优化选择，并应用于实际的工艺工程上。

[1] 郭晶玉, 邓小虎, 郑宝星, 等. Ti55531钛合金扭力臂热锻成形工艺设计及优化[J]. 精密成形工程, 2021, 13(2): 96-104.

GUO Jing-yu, DENG Xiao-hu, ZHENG Bao-xing, et al. Design and Optimization of Hot Forging Forming Process of Ti55531 Titanium Alloy Torsion Arm[J]. Journal of Netshape Forming Engineering, 2021, 13(2): 96-104.

[2] 杨天云, 张晴朗, 杨兵, 等. CAE在汽车座椅轻量化设计中的应用[J]. 精密成形工程, 2012, 4(1): 73-77.

YANG Tian-yun, ZHANG Qing-lang, YANG Bing, et al. Application of CAE in Lightweight Design of Car Seats[J]. Journal of Netshape Forming Engineering, 2012, 4(1): 73-77.

[3] 王江波, 强宝民. 基于ABAQUS圆柱壳减振装置振动特性研究[J]. 包装工程, 2017, 38(17): 112-117.

WANG Jiang-bo, QIANG Bao-min. Research on Vibration Characteristics of Cylindrical Shell Vibration Reduction Device Based on ABAQUS[J]. Packaging Engineering, 2017, 38(17): 112-117.

[4] 李炎辉, 胡青春. PET瓶基于ABAQUS的轴压分析[J]. 包装工程, 2009, 30(10): 18-20.

LI Yan-hui, HU Qing-chun. Axial Compression Analysis of PET Bottle Based on ABAQUS[J]. Packaging Engineering, 2009, 30(10): 18-20.

[5] 赵宁, 张运军, 陈天赋, 等. V5型转向节臂部锻造开裂研究[J]. 塑性工程学报, 2017, 24(3): 7-12.

ZHAO Ning, ZHANG Yun-jun, CHEN Tian-fu, et al. Research on Forging Cracking of V5 Steering Knuckle Arm[J]. Chinese Journal of Plastic Engineering, 2017, 24(3): 7-12.

[6] 章志兵, 杨明润, 王丽荣, 等. 基于CAE模型的船舶舱室自动识别高效算法[J]. 精密成形工程, 2020, 12(4): 160-165.

ZHANG Zhi-bing, YANG Ming-run, WANG Li-rong, et al. High-Efficiency Algorithm for Automatic Identification of Ship Cabins Based on CAE Model[J]. Journal of Netshape Forming Engineering, 2020, 12(4): 160-165.

[7] 刘江, 徐皓. 基于Deform 3D的长杆类汽车转向节锻模设计及锻造工艺生产验证[J]. 锻压技术, 2021, 46(2): 9-13.

LIU Jiang, XU Hao. Design of Forging Die and Forging Process Production Verification of Long-Rod Automobile Steering Knuckle Based on Deform 3D[J]. Forging Technology, 2021, 46(2): 9-13.

[8] 赵毅, 刘淑梅, 何文涛, 等. 汽车转向节热锻工艺分析及模具结构优化设计[J]. 精密成形工程, 2016, 8(3): 40-44.

ZHAO Yi, LIU Shu-mei, HE Wen-tao, et al. Hot Forging Process Analysis and Die Structure Optimization Design of Automobile Steering Knuckles[J]. Journal of Netshape Forming Engineering, 2016, 8(3): 40-44.

[9] 王德林, 陆有根, 吴兵. 三销轴叉精整底部裂纹产生和防护[J]. 精密成形工程, 2018, 10(1): 177-180.

WANG De-lin, LU You-gen, WU Bing. The Occurrence and Protection of Bottom Cracks in the Finishing of Three-Pin Shaft Fork[J]. Journal of Netshape Forming Engineering, 2018, 10(1): 177-180.

[10] STONE E, CAI J, HU Z M, et al. An Exercise in Cold Ironing as the Post-Forging Operation for Net-Shape Manufacture[J]. Journal of Materials Processing Technology, 2003, 135(2/3): 278-283.

[11] 朱怀沈, 夏巨谌, 金俊松, 等. 大模数直齿轮温冷锻精整量的优化选择[J]. 塑性工程学报, 2011, 18(1): 53-57.

ZHU Huai-shen, XIA Ju-chen, JIN Jun-song, et al. Optimization of Sizing Amount during Warm-Cold Compound Forging for Supr Gear With Big Modulus[J]. Journal of Plasticity Engineering, 2011, 18(1): 53-57.

[12] 郭嘉晨, 汪建敏, 潘小迎, 等. 基于Kriging模型的等速万向节滑套冷精整工艺的优化[J]. 锻压技术, 2017, 42(5): 176-180.

GUO Jia-chen, WANG Jian-min, PAN Xiao-ying, et al. Optimization of Cold Finishing Process of Constant Velocity Universal Joint Sliding Sleeve Based on Kriging Model[J]. Forging Technology, 2017, 42(5): 176-180.

[13] KWANGHYUN A, KANG-HEON L, JAE-SEON L, et al. Analytic Springback Prediction in Cylindrical Tube Bending for Helical Tube Steam Generator[J]. Nuclear Engineering and Technology, 2020, 52(9): 2100-2106.

[14] FARHAD A, NAYEBI A. Springback Analysis of Thick-Walled Tubes under Combined Bending-Torsion Loading with Consideration of Nonlinear Kinematic Hardening[J]. Production Engineering, 2020, 14(8): 135-145.

[15] SOHEIL Solhjoo, SHAHIN Khoddam. Evaluation of Barreling and Friction in Uniaxial Compression Test: A Kinematic Analysis[J]. International Journal of Mechanical Sciences, 2019, 156: 486-493.

[16] UTEN Khanawapee, SUTHEP Butdee. A Study of Barreling and DEFORM 3D Simulation in Cold Upsetting of Bi-Material[J]. Materials Today: Proceedings, 2020, 26(2): 1262-1270.

[17] FRAS T, RUSINEK A, PECHERSKI R B, et al. Analysis of Friction Influence on Material Deformation under Biaxial Compression State[J]. Tribology International, 2014, 80: 14-24.

[18] PERSSON B, SIVEBAEK I M, SAMOILOV V N, et al. On the Origin of Amonton's Friction Law[J]. Journal of Physics Condensed Matter, 2008, 20(39): 1-11.

[19] 秦芳, 李子亮. TC18钛合金机械支座模锻成形特性的研究[J]. 热加工工艺, 2022, 51(9): 110-113.

QIN Fang, LI Zi-liang. Research on Die Forging Characteristics of TC18 Titanium Alloy Mechanical Support[J]. Hot Working Technology, 2022, 51(9): 110-113.

[20] 孙世仁, 刘虹, 陈文琳, 等. 基于有限元软件的锻造工艺参数对牵引拉杆成形的影响分析[J]. 热加工工艺, 2020, 49(15): 68-72.

SUN Shi-ren, LIU Hong, CHEN Wen-lin, et al. Analysis of the Influence of Forging Process Parameters on the Forming of Traction Rod Based on Finite Element Software[J]. Hot Working Technology, 2020, 49(15): 68-72.

[21] 张庆旭, 刘飞, 周伟. 基于Deform的铝合金盘体件锻造工艺参数对成形性能影响的分析[J]. 热加工工艺, 2020, 49(13): 112-114.

ZHANG Qing-xu, LIU Fei, ZHOU Wei. Analysis of the Effect of Forging Process Parameters on the Formability of Aluminum Alloy Disc Body Parts Based on Deform[J]. Hot Working Technology, 2020, 49(13): 112-114.

[22] YE Xian-jue, GONG Xiao-juan, YANG Biao-biao, et al. Deformation Inhomogeneity Due to Sample-Anvil Friction in Cylindrical Compression Test[J]. Transactions of Nonferrous Metals Society of China, 2019, 29(2): 279-286.

[23] 郭宇飞, 赵康, 海永清. 面向有限元分析的三角网格布尔运算方法[J]. 系统仿真学报, 2022, 34(5): 1003-1014.

GUO Yu-fei, ZHAO Kang, HAI Yong-qing. A Triangular Mesh Boolean Operation Method for Finite Element Analysis[J]. Journal of System Simulation, 2022, 34(5): 1003-1014.

[24] JIANG Xiao-tong, PENG Qing-jin, CHENG Xiao-sheng, et al. Efficient Booleans Algorithms for Triangulated Meshes of Geometric Modeling[J]. Computer-Aided Design and Applications, 2016, 13(4): 419-430.

[25] DONNIE Curington. Real Time Data Verification of Load and Pressure Testing Using von Mises Yield Criterion for Thick Walled Tubular Products[J]. International Journal of Mechanical Engineering and Robotics Research, 2019, 8(2): 167-172.

Optimization of Cold Finishing Process for the End of Automobile Knuckle Arm

WAN Jia-xiong1,WU Jian-xiang2,YAN Yang2,DING Hua-feng1,2

(1. Hubei Key Laboratory of Power System Design and Test for Electrical Vehicle, Hubei Xiangyang 441053, China; 2. Hubei Sanhuan Forging Co., Ltd., Hubei Xiangyang 441700, China)

The work aims to obtain the relationship between the change rule of the one-way compression cold finishing and the radius and depth of the pre-deformed hole and between the friction coefficient and the rebound. The upper and lower surfaces of the forgings at the end of the knuckle arm were treated with pre-deformed grooves, and the elastoplastic finite element model of the forgings with unidirectional compression and cold finishing was established. The ABAQUS finite element software was used for numerical simulation to analyze the effects of the friction coefficient on the surface quality. The optimized process parameters were obtained. The accuracy of the simulation result was verified by experiment. The results showed that the greater the friction coefficient, the more obvious the drum shape of the knuckle arm end forging after cold finishing. When the finishing amount was 1 mm, the radius of the pre-deformed groove hole was 4 mm and the depth was 0.3 mm, the unidirectional compression was 1.1 mm and the friction coefficient was 0.2, the best surface quality can be obtained. When the friction coefficient is the same, the larger the radius of the pre-deformed groove hole, the smaller the radial displacement, and the rebound remains basically unchanged.

automobile knuckle arm; cold finishing; process optimization; rebound

10.3969/j.issn.1674-6457.2022.09.009

TG316；U463.46

A

1674-6457(2022)09-0066-07

2021–12–22

湖北省教育厅科学技术研究计划青年人才项目（Q20202602）

宛加雄（1996—），男，硕士生，主要研究方向为汽车轻量化及CAE分析。

丁华锋（1986—），男，博士，副教授，主要研究方向为汽车轻量化设计及制造技术。

责任编辑：蒋红晨