基于有限字符输入的OFDM VLC-RF 聚合系统最优能效研究

鲁姗妹，方 啸，何凌燕，李 兵，马 帅，2，3，李世银

（1. 中国矿业大学 信息与控制工程学院， 江苏 徐州 221116；2. 东南大学 移动通信国家重点实验室，江苏 南京 210096；3. 西安邮电大学 陕西省信息通信网络及安全重点实验室， 陕西 西安 710121）

0 引言

目前，我国通信产业年均耗电量已超过200亿kW·h，正在逐步向高耗能产业靠近；同时，通信能耗在电子信息行业能耗中所占的比重也在持续提高。随着我国“双碳”目标的提出［1］，节能、减耗已经成为无线通信网络发展的必然趋势［2］。能量效率（energy efficiency，EE）表示有用通信速率与总功耗的比值，是通信系统的一种关键性能指标。对于下一代无线通信网络技术来说，如何提高EE已经成为亟待解决的问题之一。

可见光通信（visible light communications，VLC）拥有从385 THz到789 THz的海量免授权带宽。作为一种能够提供照明和高速率传输的绿色通信技术，VLC已经引起了行业广泛的关注，其利用发光二极管（light emitting diode，LED）作为发射器、光电探测器（photo detector，PD）作为接收器，可以提供高吞吐量、高EE和低成本的数据通信方式。然而，由于LED 具有上升时间长和多径反射的特点，且VLC 信道具有低通特性［3‐4］，高速传输的VLC符号间将产生干扰。

为了解决低通效应问题，正交频分复用（orthogonal frequency division multiplexing，OFDM）因其对功率的适应能力强而被广泛应用到低通信道上的每个子载波上。此外，由于VLC 采用了强度调制和直接检测（IM/DD）技术，VLC 信号应该是实数且非负的。因此，采用快速傅里叶逆变换（inverse fast Fourier transform，IFFT）运算前的厄米特对称来保证信号的实值，并由直流偏置或采用非对称剪切操作产生非负信号。直 流 偏 置OFDM（direct current biased optical‐OFDM，DCO‐OFDM）和 非 对 称 限 幅 光 学OFDM（asymmetrically clipped optical OFDM，ACO‐OFDM）是两种常用的IM/DD OFDM方案［5‐7］。更准确地说，在DCO‐OFDM 中通过添加直流偏置，双极性OFDM 信号可以转换为非负信号，但是会导致信息的丢失；而ACO‐OFDM中只有奇数子载波，通过裁剪冗余的负部分来传输数据，不会造成信息损失，但牺牲了频谱效率（spectrum efficiency，SE）。与DCO‐OFDM 相比，ACO‐OFDM具有更低的误码率和峰值平均功率比［8‐9］。

然而，尽管VLC具有海量免授权带宽以及兼具照明与通信、绿色环保的优点，但其信号容易被阻塞，这可能会降低VLC 的服务质量。为了克服VLC 的弊端，将VLC系统和RF系统集成起来，综合RF和VLC的优点，如VLC的巨大带宽和RF的衍射能力传输，可以提供高速、可靠的数据信息。

目前，针对基于有限字符输入的OFDM VLC‐RF聚合系统EE的研究较少，仅文献［10］提出了一种无线电和光混合的OFDM（hybrid of radio and optical OFDM，HRO‐OFDM）方案，用于在RF和VLC链路中自适应地分配功率和带宽，其中VLC 链路采用DCO‐OFDM，对应的信道容量计算基于经典的香农容量公式。为此，本文研究具有有限字符输入的VLC‐RF聚合系统，其中VLC连接采用ACO‐OFDM，并考虑实际的照明水平。文中首先推导出有限字符输入的无闭式形式信息传输速率及其闭式下界，用这两个表达式定义了OFDM VLC‐RF 聚合系统的EE；再根据给出的EE表达式研究满足频谱效率门限、总电功率和平均光功率约束的能效最大化问题，并利用Dinkelbach‐type 算法将EE最大化非凸问题转化为一系列凸的子问题，然后在迭代过程中用内点算法解决这些问题。

1 OFDM VLC-RF聚合系统模型

在室内，下行链路通信的OFDM VLC‐RF 聚合系统对数据信息处理的过程如图1所示，其中消息I可以通过VLC 链路中具有2Nv个子载波的ACO‐OFDM与RF 链路中具有Nr个子载波的OFDM 同时传输。消息I首先被分为两部分，即Iv(kv) ={1，1，0，1，0，…}和Ir(kr) ={0，1，1，0，1，…}，并分别通过VLC 链路和RF链路在两个不同的频段传输信息；然后通过串并转换，将Iv和Ir分别分成2Nv和Nr个信号，接着进行正交幅度调制（quadrature amplitude modulation，QAM）。

图1 OFDM VLC‐RF 聚合系统信号处理过程框图Fig.1 Block diagram of signal processing process of OFDM VLC‐RF aggregation system

1.1 信号模型

在VLC链路中，子载波分配是通过将调制后的复数值分配给奇数子载波来完成的，而偶数子载波因为不传输信息，被设置为零。Xv，i表示QAM 调制后的频域信号：

在ACO‐OFDM 调制器的输出端获得实信号的一种方法是应用厄米特对称，如式（2）所示。

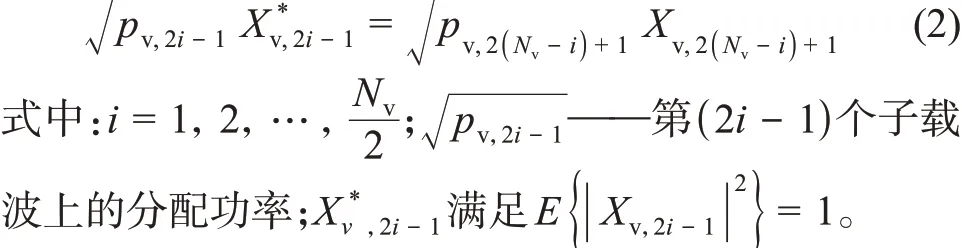
经过IFFT变换后，第k时刻时域信号可以由式（3）给出。

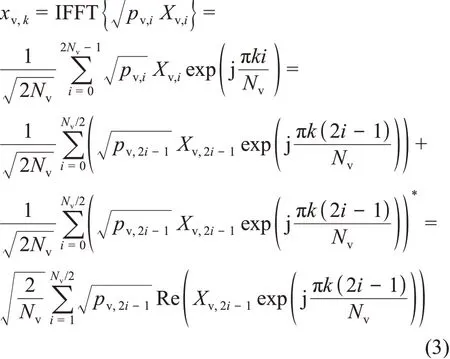
第(k+Nv)时刻的时域信号可以表示为

由式（3）和式（4）推导可得k时刻的时域信号，其具有反对称性，即

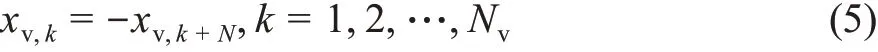
本文采用并行转换到串行和添加循环前缀的方式来防止符号间干扰。为保证传输信号是非负的，需进行限幅运算。限幅运算后的时域信号可以表示为

图2展示了ACO‐OFDM过零限幅示意。由式（5）可以看出，传输的信号满足反对称特性。虽然过零限幅后数据幅度小于零的部分被去除，但是不会导致传输数据的损失。

图2 过零限幅示意Fig.2 Diagram of zero‐crossing clipping

在RF 链路中，Xr，k表示QAM 调制后的频域信号，需要满足期望值表示第k个子载波上的分配功率，时域信号xr，k可以由IFFT变换得到。

1.2 信道模型

通常，VLC 信道包括直射链路和漫反射链路，本文采用了常用的频域VLC信道模型［11］。用Hv，i表示第i个子载波的信道增益，其中包括直射链路和漫反射链路的增益，可由式（7）给出。

式中：Hv，L——直射链路的增益；Hv，D，i——漫反射链路的增益；Δt——直射信号到漫反射链路信号之间的延时。

直射链路增益［12］定义如下：

式中：m——朗伯辐射的阶数，它是半强度辐射角ψ12的函数，表示为光学滤波器的增益；g(θ)——集中器增益；Ap——接收器的物理面积；d——从VLC 的接入点到光接收机的距离；φ——辐射角度；θ——入射角；Ψ——VLC 链路接收机视场角。

频域中漫反射分量［13］的定义为

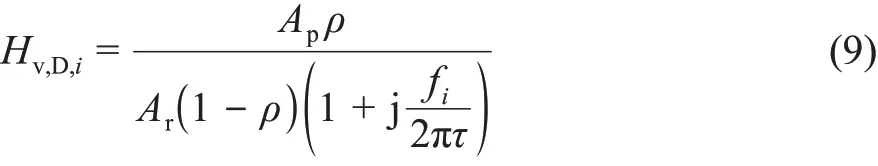
式中：Ar——房间表面积；ρ——墙壁的反射率；τ——指数衰减时间。

RF 链路中，Gr，k(fk)表示第k个子载波的信道增益［14］，Gr，k(fk)可由式（10）给出。

式中：hr——具有独立瑞利分布的小尺度衰落增益，平均功率增益为2.46 dB［15］；L(dr，k)——距离为dr，k的大规模衰落损失［15］，其由式（11）给出。

式中：dr，k——用户与第k个子载波间的距离；XSF——由于大规模阻塞导致的阴影衰落损失，XSF~CN(0，σ2)；dB——断点距离；LFS(dr，k)——自由空间损耗，其可由式（12）表示。

式中：fk——第k个子载波的频率。

1.3 系统约束

在接收端，移除所接收信号的循环前缀并执行IFFT，再通过QAM解调器解调得到原始比特流。接收到的数据信息Yv，2i-1和Yr，k可由式（13）给出。

调光控制是VLC链路的一个特征，不仅需要确保眼睛安全而且还需要满足实际照明需求［17‐20］。Po表示平均光功率阈值，平均光功率应满足

2 OFDM VLC-RF聚合系统信息传输速率

2.1 信息传输速率

根据文献［21］，在VLC 链路中，第(2i- 1)个子载波的传输速率为

在RF链路中，第k个子载波的信息传输速率为

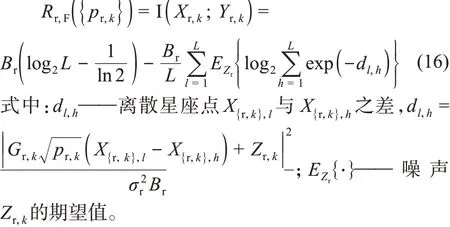
因此，OFDM VLC‐RF 聚合系统的信息传输速率为

2.2 信息传输速率下界

由于式（15）和式（16）不是闭式表达式，本文通过研究计算复杂度高的蒙特卡洛方法得到信息传输速率。为了降低计算复杂度，本文进一步研究了低复杂度的功率分配方案。

式（15）中的期望项的上限［21］为

令Rv，L({pv，2i-1})表示第(2i- 1)个子载波信息传输速率下界，则基于有限字符输入的VLC链路的信息传输速率下界可表示为

令Rr，L({pr，k})表示RF 链路第k个子载波信息传输速率下界，其计算如下：

因此，基于有限字符输入的OFDM VLC‐RF 集合系统信息传输速率下界可表示为

3 OFDM VLC-RF聚合系统最优能效研究

本文提出一种基于有限字符输入的OFDM VLC‐RF 聚合系统的最优能效设计，其能最大化地满足SE门限、总电功率约束以及平均光功率约束的EE。令υ表示OFDM VLC‐RF聚合系统的SE门限，其可表示为

OFDM VLC‐RF 聚合系统的EE 最大化问题可表示为

式中：Pc——系统内总功耗值。

本文将利用式（23）分别研究基于信息传输速率和信息传输速率下界两种情况下的最优能效EE。

3.1 基于信息传输速率的最优能效

基于信息传输速率的EE可以表示为

此外，基于式（6）可知，平均光功率约束可以表示为

将式（25）代入式（14），可以得到平均光功率约束为

因此，在电功率约束和平均光功率约束以及SE门限下，基于有限字符输入的EE最大化问题可以表示为

式（28）中的SE 门限约束和目标函数没有闭式表达式，可以使用复杂度较高的蒙特卡洛仿真来实现。

式（28）的目标函数的分子对其输入功率而言是严格凹的，分母对输入功率是仿射的；另一方面，式（28）中的SE 门限约束是凸的，所以式（28）是典型的凹‐线性分式问题。本文采用Dinkelbach‐type 迭代算法［22］来处理这个非凸问题，主要思想是首先通过将式（28）转变为一系列凸的子问题，然后在每次迭代中利用内点法求解这些凸的子问题，最终可以获得式（28）的高质量局部最优解［23］。

为了解决凹‐线性分式问题，本文重新定义一个新函数F(pv，2i-1，pr，k，μ)。

式中：μ——实变量，其可通过每次迭代更新获得。

在式（28）的约束条件下，可以通过找到等式F(pv，2i-1，pr，k，μ)= 0的根来求得式（28）的最优解。

在每次迭代时，给定μ值，式（28）的子问题可以表示为

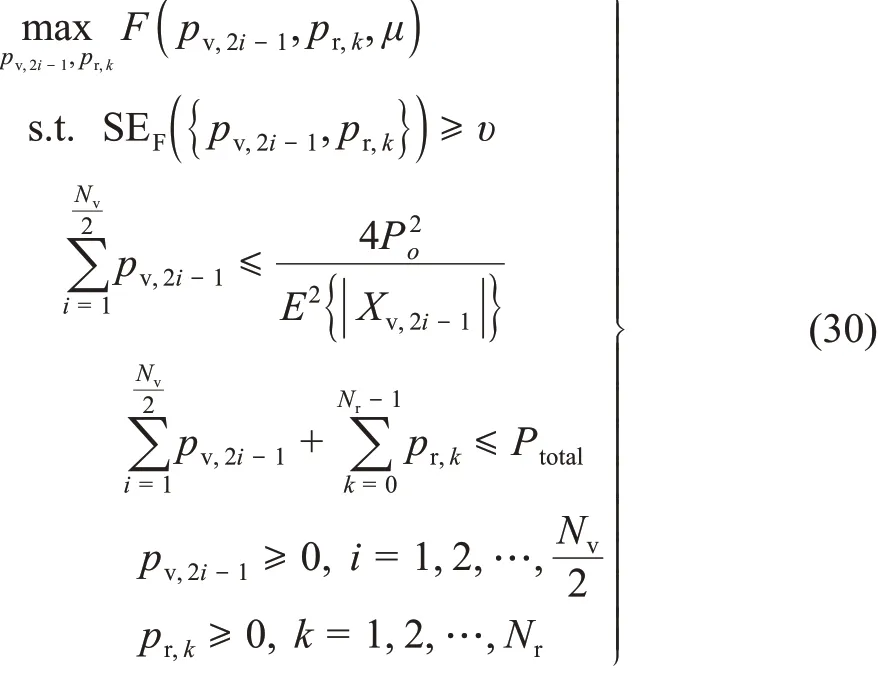
对于固定的μ，式（28）是pv，2i-1和pr，k的凸优化问题。所以，最优功率pv，2i-1和pr，k可以通过内点算法获得，具体如表1所示。

表1 Dinkelbach‐type 算法Tab. 1 Dinkelbach‐type algorithm

3.2 基于信息传输速率下界的最优能效

在式（28）中，目标函数和SE门限约束需要用高计算复杂度的蒙特卡洛实验来求解。为了降低计算复杂度，本文利用信息传输速率下界式（19）和式（20），给出了OFDM VLC‐RF聚合系统对应的EE定义：

此外，根据式（22）和式（27），EE 最大化问题，即式（23），可以重新表述为

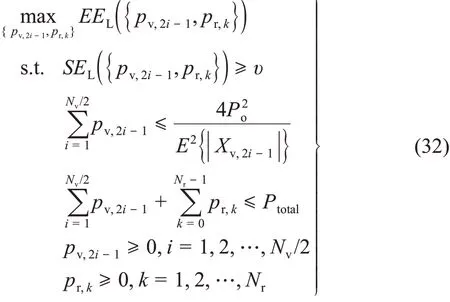
式（32）的目标函数的分子是凹且可微的，分母是线性函数，则式（32）是凹-线性分式问题。所以式（32）也可以使用Dinkelbach‐type算法求解，即通过将式（32）转变为收敛于局部最优点的一系列的凸子问题，然后在每次迭代中利用内点法求解这些凸的子问题；最终可以获得式（32）的高质量的局部最优解。具体过程与3.1节类似，此处不再具体描述。

4 仿真结果与分析

本节主要描述一些系统约束对OFDM VLC‐RF聚合系统最优能效的影响，并给出了仿真结果图，然后进一步对仿真结果的变化情况做出了分析。

假设房间大小为5 m × 5 m × 3 m，房间内配备了4个LED和1个射频发射天线，4个LED的位置分别为（1.5 m，1.5 m，3 m），（1.5 m，3.5 m，3 m），（3.5 m，1.5 m，3 m）和（3.5 m，3.5 m，3 m），VLC接收端位置为（0.5 m，1 m，0）。仿真基本参数见表2 中，因为RF 链路的信道是随机的，仿真过程采用蒙特卡洛实验，次数为5 000次。本文将基于信息传输速率的能效定义为EF，将基于信息传输速率下界的能效定义为EL。

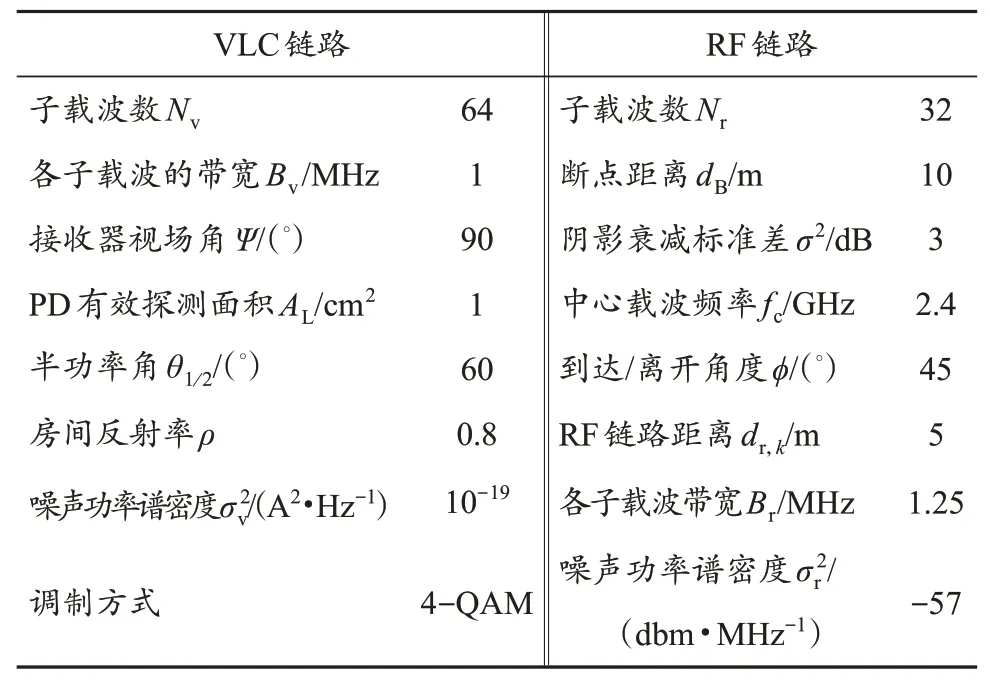
表2 仿真参数表Tab.2 Table of simulation parameters

图3（a）和图3（b）展示了在总电功率Ptotal=0.5 W、平均光功率约束Po=1 W、SE门限υ=70 Mbit/(s ⋅Hz)限制下，EF和EL的分配功率pv，i与信道增益Hv，i随着子载波i变化的情况，以及RF 链路EF和EL的分配功率pr，k与信道增益Gr，k随着子载波k变化的情况。图3（a）表明，分配功率pv，F与信道增益呈正相关，这是因为系统会优先给信道增益较大的子载波分配功率，从而达到满足SE 门限υ=70 Mbit/(s⋅Hz)的最大能效。对于EL来说，系统需要更多的功率来满足SE门限υ，而信道增益较大的子载波对应的信息传输速率已经达到上限，所以功率几乎不会分配给信道增益较大的子载波，反而将额外的功率分配给信道增益较小的子载波，所以pv，L呈上升趋势。图3（b）表明虽然RF信道增益是随机的，还是可以看出RF 链路EF和EL的分配功率pr，F和pr，L与VLC链路具有相同的表现形式；RF链路中EF的每个子载波k分配的功率高于EL中分配的功率，这是因为

图3 VLC 和RF 链路EE 分配功率与相应的信道增益随着子载波的变化Fig.3 Allocated power and channel gain of VLC and RF link EE versus subcarrier

图4说明了在平均光功率约束Po=1 W和SE门限υ=50 Mbits/(s ⋅Hz)下，EF和EL随总电功率约束Ptotal变化而变化的情况。从图4 中看到，随着Ptotal的增加，EF和EL先单调增加然后保持不变，其原因是EF和EL受Po=1 W的限制。此外，可以看出，由于Ptotal的增大，EL越来越接近EF，所以EL可以作为EF一个很好的低复杂度近似。

图4 EF 和EL 随着总电功率约束Ptotal 变化的情况Fig.4 Energy efficiency EF and ELversus total electric power constraint Ptotal

图5说明了EF和EL随SE阈值υ变化的情况，其中Ptotal=10 W，Po=1 W。从图5 可以看出，EF和EL都先保持稳定，然后随着SE 阈值υ的增加而减小。这是因为当SE阈值υ较小时，系统能效达到最大时所需要的分配功率很容易达到SE 阈值υ的要求，因此EF和EL保持不变。当SE 阈值υ变大时，需要消耗更多的分配功率来满足SE 阈值υ，因此EF和EL降低。此外，可以看出，随着SE门限υ的增加，EL越来越接近EF。

图5 EF 和EL 随着SE 门限υ 变化的情况Fig.5 Energy efficiency EF and ELversus SE threshold υ

图6说明了在受到Po=0.5 W 的限制下，本文所提方案对应的EF和文献［24］提出的等功率方案对应的EF随着Ptotal的变化。如图6 所示，随着Ptotal逐渐增加，两种方案对应的EF都在增加，但本文所提方案对应的EF优于等功率分配方案对应的EF，并且随着Ptotal的增大，这种优势更加明显。

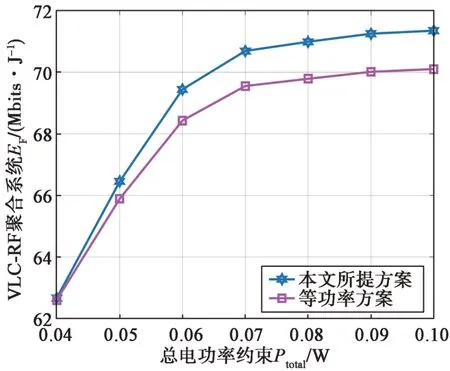
图6 本文提出方案对应的EF 与等功率方案对应的EF 随着总电功率约束Ptotal 变化的情况Fig.6 The energy efficiency EF of the presented scheme in the thesis and equal power scheme versus total electric power constraint Ptotal

表3描述了在Matlab2016b 仿真软件，2.30 GHz、2.29 GHz 双CPU 和128 GB RAM 存储器环境下进行的基于信息传输速率的EF和基于信息传输速率下界的EL的仿真时间比较。

表3 EF 和EL 计算时间的比较Tab.3 Comparison with calculation time of EF 和EL

通过图4和图5可以观察到，基于信息传输速率的EF要优于基于信息传输速率下界的EL；但是，从表3可以看出基于信息传输速率的EF的计算时间要明显长于基于信息传输速率下界的EL的。结合图4、图5和表3可知，基于信息传输速率下界的EL可以作为基于信息传输速率的EF一个很好的低复杂度近似。

5 结语

本文推导出了无闭式表达式的信息传输速率及其具有闭式表达式的下界，在此基础上给出了OFDM VLC‐RF 聚合系统的能效表达式；并在SE 门限、平均光功率和总电功率约束下，研究能效最大化非凸问题；同时，采用Dinkelbach‐type型算法，将能效最大化非凸问题转化为一系列凸的子问题，并在迭代过程中通过内点法求解每个凸的子问题。仿真结果表明，基于信息传输速率下界的能效可以作为基于信息传输速率的能效的一个很好的低复杂度近似，且SE门限较大时聚合系统的能量效率会降低。

本文在基于有限字符输入的OFDM VLC‐RF聚合通信的能效研究中，考虑的是等概率地从离散星座集中获得传输信号。在未来，可以考虑非等概率地从离散星座集中获得传输信号的情况，并基于此研究最优能效。