“双碳”目标背景下面向并网型微电网的虚拟电厂优化调度

2022-09-07赵晋辉李玉凯韩佳兵赵钧梁聪

新型工业化 2022年7期

赵晋辉，李玉凯，韩佳兵，赵钧，梁聪

1.南瑞集团有限公司（国网电力科学研究院有限公司），江苏南京，211106； 2.北京科东电力控制系统有限责任公司，北京，100192

0 引言

为实现“碳达峰、碳中和”目标，建设清洁低碳安全高效的能源节约型社会，习近平总书记在中央财经委员会上提出“实施可再生能源替代行动，构建以新能源为主体的新型电力系统”，分布式电源（distributed resources，DR）以其经济、环保、安全、灵活等优点在“双碳”目标布局中得到广泛应用[1-4]。并网型微电网将DG、储能单元及负载单元组成一个既能并网参与电力系统统一调配，又能在需要时与外网断开独立运作的系统，一定程度上解决了DG容量小、数量大、分布不均导致的单机接入成本高、管理困难的问题。但由于并网型微电网的主要目标是让DG能够就地消纳以减小电能传输损耗，因此受地理区域限制，大规模、多区域DG的有效利用存在一定局限性。在此基础上，虚拟电厂（virtual power plant，VPP）通过高级测量技术、控制技术、通信技术等手段将多种分布式发电单元、可控负荷以及储能单元聚合起来[5-6]，以一个特殊电厂的身份参与电网运行协调管理和电力市场互动[7]，实现电源侧多能互补和负荷侧柔性互动，为真正实现DG的大规模并网提供了切实可行的解决方案。

为充分发挥VPP在DG消纳、负荷管理等方面的优势，需制定合适的优化调度策略以协调VPP内成员、网络的运行。目前有关VPP优化调度的研究主要是在对各类分布式能源出力预测的基础上制定其最优调度策略，以达到VPP内运行效益最大化的目的。杨毅等人的研究[8]对并网型微电网的经济效益、电压质量和电网调峰服务等方面的能力进行了综合考虑，在原有的粒子群算法基础上进行改进，大幅提高了微电网系统的运行水平；杨秋爽等人的研究[9]对风电、光伏和电储能三类成员的协同运行方式进行了研究，得出了适当弃风弃光并利用电储能设备进行调节可有效提高微电网经济效益的结论；JULW等人的研究[10]建立了包含风电、储能等分布式资源的VPP调度模型，以实现多能资源的互补；Kuzle I等人的研究[11-12]引入一个以VPP利润最大化为目标的混合整数线性规划（MILP）模型来解决内部VPP调度问题；范松丽等人的研究[13]则结合随机模拟和遗传算法进行求解并探讨了VPP协调运行过程中如何综合考虑系统的经济效益和运行风险问题。在“双碳”目标背景下，碳排放配额将成为决定发电主体市场竞争力的核心要素，而VPP中的燃煤/气发电机组、储能装置等成员是碳排放配额的主要受限对象。因此，本文提出“双碳”目标背景下考虑碳排放成本的VPP优化调度模型，旨在为VPP在“双碳”目标布局下的推广和应用提供支撑。

1 “双碳”背景下的VPP模型

1.1 系统架构

本文研究的VPP主要包括光伏、风电等典型DG以及用户侧储能和负荷等成员。在实际运行中，由VPP调控中心综合考虑调度成本和碳排放成本，对各个成员的运行进行协调优化，以实现VPP的经济、高效运行。整个VPP通过联络线接入外电网，能够和外电网上的其他VPP进行信息与能量交互，还可以与主网进行能量交互（图1）。

1.2 供能单元模型

（1）光伏发电系统。光伏（photovoltaic，PV）发电系统的出力可根据其标准出力和实际环境条件进行计算[14]，如式（1）所示：

式中，Ppv为系统出力，Pstc为系统标准出力（I=1.0kW/m2，θstc=25℃）；αθ为温度系数；θt为t时刻光伏面板的温度；It为t时刻实际太阳辐照强度。由于光伏发电系统本身的特点，通常将其边际成本视为0。

（2）风力发电系统。采用韦布尔分布对风电机组（wind turbines，WT）的出力进行计算。首先利用风电机组历史风速数据对尺度参数ξ与形状参数k进行拟合，设随机变量为v，如式（2）所示[13]：

式中m为风速。在此基础上，风电机组的出力可由式（3）表示：

式中：Pwt为风电机组的原始模拟出力；mmin、mrated与mout分别为风电机组切入风速、额定风速与切出风速；R为风电机组的额定出力。由于风力发电机组本身的特点，通常将其边际成本视为0。

（3）分布式发电系统。分布式发电系统主要包括燃气轮机发电系统和用于调峰的内燃机发电系统、柴油机发电系统等。其发电主要成本CMT包括燃料和维护等各类成本，如式（4）所示：

式中：PDG(t)为t时刻机组的出力；ρDG、γDG、 DG为分布式发电系统的单位运行成本系数。

（4）电储能系统。电储能设备在运行过程中通常有三种工况，即充能工况、释能工况和停运工况。其中，前两种工况的数学模型如下：

式中：下标B代表电池储能设备；δB为储能过程中的消耗率；ηin和ηout分别是输入转化效率和输出转化效率；Δt是时间步长；Pin和Pout分别是能源输入量和能源输出量。

（5）碳排放模型。在我国“双碳”背景下，政府既可以通过拍卖出售配额，也可以向相关主体免费发放配额。其中免费分配法主要包括历史数据法、基准线法和基于产出与排放强度的配额分配法三种。由于基准线法在国内应用较广，故本文选取其作为碳排放配额分配方法，计算方法如式（7）~（8）所示：

式中：Pt为虚拟电厂在时刻i的总发电量；PDG,i(t)为第i个DG在t时刻的出力；m为DG总数；Pbat,j(t)为第j电储能系统在t时刻的电功率；n为电储能系统总数；EQ为虚拟电厂总碳排放配额；ε为单位电量排放配额。

在虚拟电厂中，由于风力发电系统和光伏发电系统的碳排放量约等于0，因此，系统的碳排放主要指的是分布式发电系统和电储能系统的碳排放情况，虚拟电厂的碳排放量可由式（9）计算得出：

式中：EC为虚拟电厂各个成员24小时碳排放量之和；δDG,i为第i个DG的碳排放强度；δbat,j为第j个电储能系统的碳排放强度。

据工业碳排放公式，虚拟电厂的碳排放成本可由式（10）计算得出：

式中：CCE为系统碳排放成本；μ为虚拟电厂参与碳交易的单价；d为碳排放量阶梯范围系数；k为碳交易单价阶梯增长系数。值得注意的是，当虚拟电厂存在EC＜EQ时，系统可通过出售EQ与EC之差的碳排放配额以获得盈利。

1.3 约束条件

（1）设备输出功率约束。

式中，Pi,max和Pi,min分别为VPP供能单元i的有功出力上限和下限。

（2）电储能系统运行约束。电储能系统的充能工况和释能工况相互独立，且均可在允许范围内自由调整充/释能功率，有以下约束：

电储能系统的充能、释能工况时长应当合理安排，做到系统能量能在一定周期内消耗完毕再重新充满，达到系统利用效率的最大化。因此有如下约束：

式中：T是一个充能和释能工况的完整周期；是电储能系统在充能工况下的损耗。

（3）爬坡率约束。

式中：Pi,t-1为燃气轮机、内燃机等分布式发电系统在（t-1，t)时段内的出力，和分别为其最大爬坡上升功率和爬坡下降功率。

（4）电功率平衡。

整个互动过程中，需满足电能供给量与负荷的平衡约束，如式（15）所示：

其中，Pload(t)、PPV(t)、PWT(t)、PGT(t)、PIC(t)、PST(t)分别为用户侧电负荷功率、光伏发电系统功率、风力发电系统功率、燃气轮机发电系统功率、内燃机发电系统功率和电储能系统功率，Pcut(t)为系统在t时段的切负荷量。

（5）联络线容量约束。

式中，Pgrid,max为VPP与大电网间联络线允许的最大传输功率。

（6）系统失荷率约束。

式中：λLPSP表示虚拟电厂的失荷率（loss of power supply probability，LPSP），是评估供电系统供电可靠性的重要参数。为系统运行工况下允许的最大失荷率，Tsch为一个调度周期，而WLPSP则是一个调度周期内的总失荷量，在t时段系统负荷完全满足时，λLPSP为0，反之则为λLPSP=Pcut(t)Δt。

2 面向并网型微电网的虚拟电厂优化调度策略

2.1 运行方式及策略

考虑碳排放成本的VPP运行流程如图2所示。

2.2 优化目标

虚拟电厂运行优化的总体目标函数如下：

式中：CVPP、CPV、CWT、CGT、CIC分别表示虚拟电厂系统、光伏发电系统、风力发电系统、燃气轮机发电系统和内燃机发电系统的运行成本，CCE是系统的碳排放成本。

2.3 求解方法及流程

由于前文获得的是一个混合整数非线性优化模型，为提升其优化速度，采用周灿煌等人的研究[16]中提出的线性化方法将其转化为混合整数线性模型。

对VPP的优化调度目标优化方法，首先，定义2个评估指标来分别评估VPP在经济运行和碳排放方面的效益；其次，采用多目标粒子群算法（multi-objective particle swarm optimization，MOPSO）对该系统进行优化，得到一系列可行的Pareto解；最后，通过对Pareto解集中的多个解进行对比计算评估以得出最优解（图3）。

3 算例分析

3.1 运行方式及策略

采用风/光/内/燃/储并网型微网系统进行优化调度，该系统由1个50MW风电场、1个60MW光伏发电场、2台100MW燃气轮机、1台10MW内燃发电机组以及45MW的电储能系统组成，其中将电储能系统在充能和释能工况下的效率均取为95%，初始荷电状态为0.18，碳排放强度为0.4。天然气价格为2.28元/m3，系统允许最大失荷率λLPSP=0，不可控分布式发电机组和可控分布式发电机组参数分别见表1和表2。系统输电线路损耗率为3%，不考虑系统内部损耗。

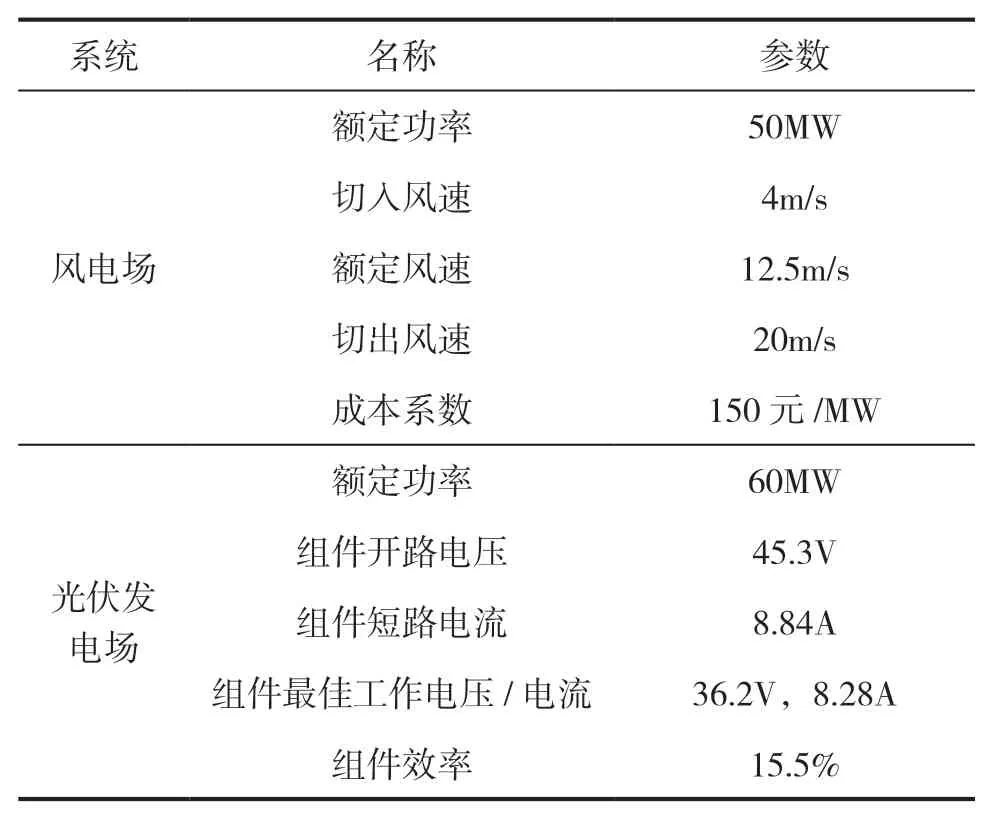
表1 不可控分布式发电机组参数

案例采用的典型日电负荷、风力发电功率及太阳辐照度预测曲线如图4所示。

VPP与电网间的购电电价采用分时电价机制，如图5所示。

本文所使用的算法迭代次数设定为300次，种群规模设定为100。在算例的碳排放模型中，设定μ=50元/t，d=40t，k=25%。本文所建立的虚拟电厂混合整数非线性优化模型在计算中采用商业求解器CPLEX进行求解，所采用的计算机为Intel Xeon 4216 @3.2GHz、64GB。

3.2 结果分析

在系统调度过程中，一方面需要分配燃气轮机、调峰用内燃机和电储能系统的出力以降低系统运行成本，另一方面需要利用电储能系统的充放电使系统保持平衡，各个DG出力的优化结果如图6所示。其中，为更好地展示储能系统对负荷波动和清洁能源出力波动的平衡作用，将电负荷和储能系统出力（充电为负值，放电为正值）之和视为折算负荷。

从图6的优化结果中可以看出，本文所提算法能够调节虚拟电厂的运行以实现对用户负荷的良好适应。由于每个时段内的不同机组单位运行成本和碳排放成本均不同，故每个时段的出力组成也会有明显差异。在19：00前，由于机组出力上下限约束，虚拟电厂使用不同分布式发电机组作为系统的主要电源。同时，由于光伏发电系统和风力发电系统的边际成本和碳排放成本均为系统内最低，虚拟电厂系统始终优先使用二者来满足用户负荷。

表2 可控分布式发电系统参数

经过优化，能够提升VPP的总体收益，详见表3。

表3 VPP效益

从表3中可以看出，经过优化调节后，通过对风电、光伏等可再生能源的协调调度，弃风率由14.4%降低至5.0%，弃光率由38.6%降低至19.9%，有效提高了清洁能源消纳水平。同时，可控分布式发电机组成本从1,792,534.75元降低至1,721,112.21元，提升了3.98%，“双碳”成本也从原来的1,845.22元下降至-1,532.55元，实现了碳排放成本的由正转负，即可通过出售碳配额进行获益。上述结果表明本文所提算法能有效通过虚拟电厂DG之间的协同调度，降低VPP的碳排放成本以及清洁能源的未利用量。VPP调度的碳排放量与成本结果如图7~8所示。

由图8可以看出，调度后的碳排放成本在24小时内整体均呈现下降趋势。特别是在00：00-07：00和9：00-16：00两个时段内，通过对光伏发电、风力发电和储能系统的利用，碳排放成本得到大幅降低。说明该调度模型能够结合历史数据和电储能系统的运行状态，提出系统内成员的优化运行策略，显著降低VPP的碳排放成本。