正态分布无偏估计相关的一个极限定理

魏昙荣， 曾振柄

(上海大学理学院，上海 200444)

1 引 言

众所周知，正态分布N(μ，σ2)中，样本方差s2是σ2的无偏估计，但由于参数估计的无偏性一般不具有不变性，因此，s并不是σ的无偏估计.通常，人们利用修偏技术，计算出修偏系数

来构造正态标准差σ的无偏估计cns[1].事实上，修偏系数并不是唯一的[2]，这里只研究cn.在证明t分布趋于正态分布的时候，一般用到该修偏系数下面的一个性质.

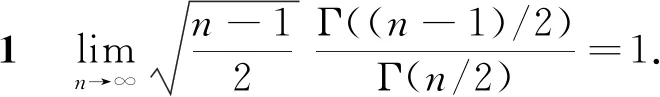
有学者已计算证明Es单调递增收敛于σ[3]. 这个命题说明s是σ的渐近无偏估计，即在样本量足够大时，可以将未修正的s认为是σ的一个较好的估计[4]. 注意到，cn是n的函数，当n趋于无穷时，Es单调递增收敛于σ，说明cn收敛于1[5]. 在此，本文将证明一个比命题1更强的定理.

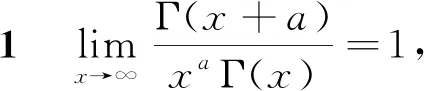
在定理1的证明过程中，利用Hölder不等式构造了两个辅助函数，借助Gamma函数的性质和两边夹定理给出证明. 在数理统计学中，命题1和定理1有个重要的应用，就是证明下面的命题2.

命题2当样本量n足够大时，t分布近似于标准正态分布N(0，1)分布.

这个结论，也出现参考文献[6-9]中，这是一个更广为人知的性质，不过上面这些书中，都没有给出严格证明，有的是用图像加以说明，有的书指出当n大于30时，t分布的形态就已经与标准正态分布无异了. 若想严格证明，可以利用Stirling公式、Wallis公式以及特征函数给Gamma函数的一个等效无穷乘积定义，即出该命题的证明.这里，利用定理1和修偏系数的收敛性即可证明命题2.最后，利用定理1，证明关于

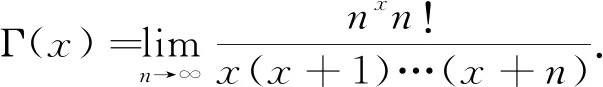
这个性质是在1729年Gauss给出的[10]. 但本人在参考文献[10]中还没有找到严格证明.

2 定理1的证明

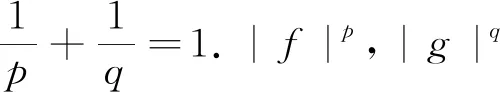
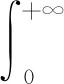
于是，上述不等式就写成Γ(x+a)≤xaΓ(x)，将该式中的a换成1-a，x换成x+a，得到

Γ(x+1)≤(x+a)1-aΓ(x+a).

把上面两个不等式组合在一起，得到

整理得

上式两边取极限，即得

3 命题1，2，3的证明

这里，将应用定理1对前述的三个命题进行一一证明.

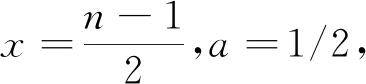
于是有

即

得证结论.

命题2的证明命题1修偏系数cn的收敛性有个重要的应用就是对在大样本情况下， t分布近似于标准正态分布N(0，1)分布的证明.

设t分布的概率密度函数为

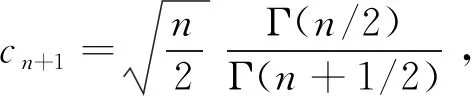
因此，对于任意实数t，由命题1可知，当n趋于无穷大时

命题3的证明这是1729年Gauss提出的Γ(x)函数的等效无限乘积定义. 这里，利用定理1给出该定义的证明.

(i) 当x=1，2，3，… 时， Γ(x)=(x-1)! 因为

结论正确.

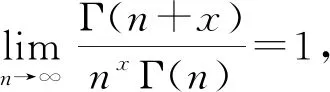
而

Γ(n+x)=Γ(n-1+x+1)=(n-1+x)(n-2+x)Γ(n-2+x)

=…=(n-1+x)(n-2+x)…xΓ(x).

于是

当然

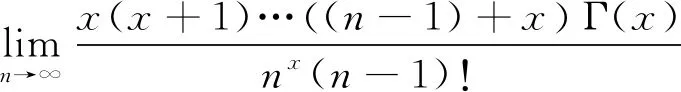
即得

于是得证.

(iii) 若x>1，记x=[x]+{x}，这里[x]是不超过x的最大整数， 0<{x}<1，于是由(ii)知

两边同乘以([x]-1+{x})([x]-2+{x})…({x}+1){x}，为方便记{x}=a，则有

([x]-1+a)([x]-2+a)…(a+1)a·Γ(a)

推论1得证.

4 结 论

推广了正态分布中标准差无偏估计的修偏系数的一个极限性质，给出了教科书中两个常见、但无严格证明的两个性质，以及Gamma函数的一个等效无限乘积定义.

致谢本文作者感谢黑龙江大学数学科学学院数学与应用数学系王士模教授和上海大学理学院数学系曾振柄教授在文章写作过程中给予的启发和悉心指导.