确定板带轧机实际油膜厚度补偿的方法

周伟文，熊佑发，王毅俊

（马鞍山钢铁股份有限公司设备部，安徽马鞍山 243000）

1 前言

大多数的板带轧机的支撑辊都会使用油膜轴承。（图1 所示）其在运转中轴颈和轴承衬套之间被一层完整的压力油膜隔开，形成液体摩擦状态。低速状态下，轴颈贴近油膜轴承衬套外壁沿旋转。随着支撑辊旋转速度的提高，油膜油充满并包裹住整个轴承，并使得轧辊逐渐趋于自身中心线方向旋转移动，油膜厚度变化量ΔOf变大，油膜厚度与轧机的轧制速度成正比。当轧制力较大时，会抵消一部分油膜压力，使得轧辊逐渐趋于衬套外壁方向旋转移动，ΔOf变小，油膜厚度与轧机的轧制力成反比。尤其在轧制过程的加减速阶段，速度和轧制力变化较大，油膜厚度变化比较明显。

图1 轧制速度、轧制力对油膜的影响

辊缝和轧制力的控制是AGC 模型的核心，（见图2）当轧机加速时，油膜变厚ΔOf变大，实际辊缝变小，使轧机的弹性曲线向左移，进而稳定轧制点也向左移动，钢板减薄Δh1，同时轧制力变大，通过压力传感器反馈至厚控系统中误判断钢板在该部分变厚Δh2，输出压紧辊缝指令以保证该部分钢板厚度不变，调整后轧制力会进一步增大ΔP；反之，实测压力减小，调整后压力进一步减小。可见压力AGC 不但无法消除油膜厚度变化的影响，相反会变得更糟。所以轧制过程中需要对因油膜厚度变化造成的辊缝变化进行实时反向厚度补偿，使得辊缝实时保持不变［1］。

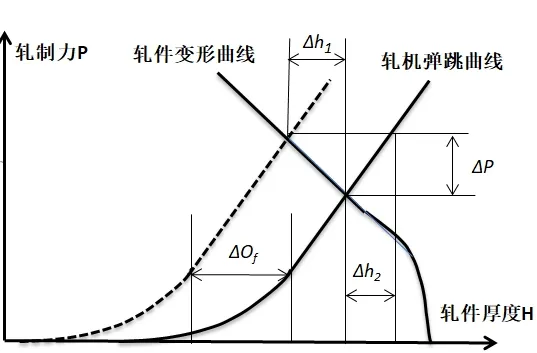
图2 油膜厚度对带钢厚度变化影响p-h 图

在油品及设备条件不变的情况下，油膜厚度主要决定于支撑辊速度及轧制力。对辊缝的影响可分为速度影响和轧制力影响这两部分来考虑。油膜厚度补偿功能是通过AGC 辊缝位置闭环控制来保证轧机速度和轧制力变化过程中辊缝的恒定不变。这个补偿量由辊缝控制功能中油膜计算模型来完成，分成速度补偿和轧制力补偿两个部分。

2 实际油膜的计算模型

由于油膜厚度不能直接测量，因而需要采用轧辊空压靠的方法间接求出油膜厚度。假设忽略轧辊磨损和热膨胀的影响，只考虑油膜厚度补偿因素的轧机弹跳方程为：

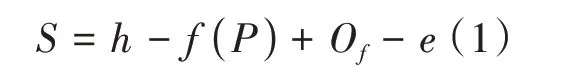
式中：S——设定辊缝，mm；

h——出口带钢厚度，mm；

P——轧制力，kN；

f（P）——由轧机的弹跳方程得出的轧机弹跳值；

Of——相对油膜厚度，mm；

e——轧辊压扁补偿量。

当轧机空压靠时出口厚度h为0，则：

轧机以两种不同的转速旋转，油膜和轧制力都会发生变化可得：

为保证辊缝不变：S1=S2，由（3），（4）可得：

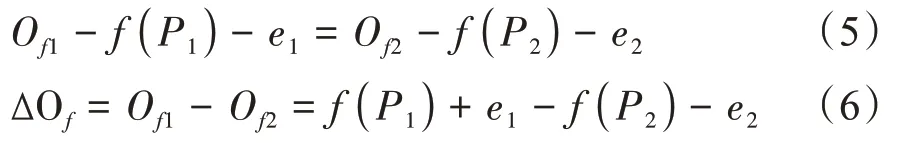
已知轧机的弹跳方程为：

式（7）中C1、C2、C3为弹跳方程的相关系数。

解方程可得在轧制力P下的弹跳值：

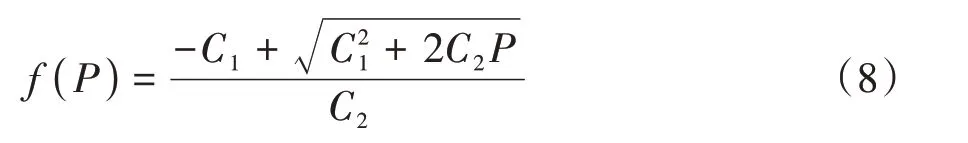
已知工作辊弹性压扁公式：

式中：R——轧辊的半径；

LB——支承辊辊身长；

v1，v2——轧辊的泊松比；

E1，E2——轧辊的杨氏模量。

由式（6）、（8）、（9）可得实际油膜的计算模型为：

3 速度补偿模型：ΔOf-NB关系方程

速度的变化会影响油膜厚度，反过来油膜厚度变化也会影响轧制力变化，它们之间是耦合关系，为了真实的反映的油膜变化补偿值ΔOf与支撑辊线速度（NB）的关系，首先设定一个基准不变轧制力，通过AGC 压力环尽量保持轧制力波动较小。在不考虑轧制力变化前提下得出ΔOf-NB关系方程。

表1汇集了各类文献中的各种ΔOf-NB模型的表达式。式中C4、C5表示回归分析常数。我们对这三个方程统计准确率在实际操作过程中进行了比较［2］。

表1 不同ΔOf-NB表达式精确度的比较

根据以上分析：

的模型计算值与实测值相当接近，式中的C4、C5可以利用空压靠方法求出。

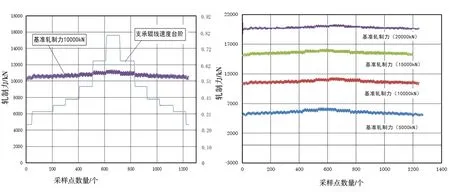
图3 采集过程示意图

下面以零标时的轧制力15 000 kN 下采集的数据为例，整个过程共采集1195 组数据，由于现场环境的影响，所采集的数据波动较大，采用五点三次平均法对数据进行了光滑处理（图4）。

图4 四个设置的轧制力

3）表（2）中，随机在支承辊线速度采集值内选取数据序号第49 组值中的NB值和P 值设定为NB1=0.240291（m/s），P1=15 485.6509 kN。P、NB为采集的实时轧制力和支撑辊的速度值，通过式（10）计算出相应的油膜变化补偿值ΔOf。

4）图5 所示在零标轧制力为15 000 kN 下油膜变化补偿值ΔOf-NB之间的关系油膜-速度方程。同理还可以得出5 000 kN、10 000 kN、20 000 kN 轧制力下的油膜-速度方程（表3）。

图5 数据的光滑处理结果

下面举例对2250 热轧精轧机F1 机架空载测试以及数据处理过程做详细的介绍：在设定的轧制力下，手动按图（3）中的13 个速度台阶（0.24、0.32、0.36、0.40、0.48、0.64、0.80、0.64、0.48、0.36、0.32、0.24）升降支撑辊速度，同时采集NB与ΔOf的数据，同时还必须考虑这些波动对油膜厚度的影响，按式（10）来处理实际的ΔOf值。

1）测试条件：全辊面压靠；工作辊、支承辊冷却水打开；弯辊设定为“平衡”、窜辊为“0”；精轧机手动调速；输入工作辊、支承辊辊径参数。

2）手动设置四种5 000 kN、10 000 kN、15 000 kN、20 000 kN 四个轧制力。其中15 000 kN 是F1 轧机零标时的轧制力。在每个轧制力下，为避免支承辊偏心对辊缝数据的影响，在速度波动稳定后开始采集，每个速度台阶采集时间大于支承辊旋转一周的时间，工作辊的转速原则上不能低于100 m/min。

表4 为根据表3 不同轧制力下ΔOf-NB曲线方程中选取7个NB速度代入后计算出的对应的油膜补偿值ΔOf。

表3 不同轧制力下的ΔOf-NB的关系式

表4 不同轧制力下ΔOf油膜补偿计算值 单位：mm

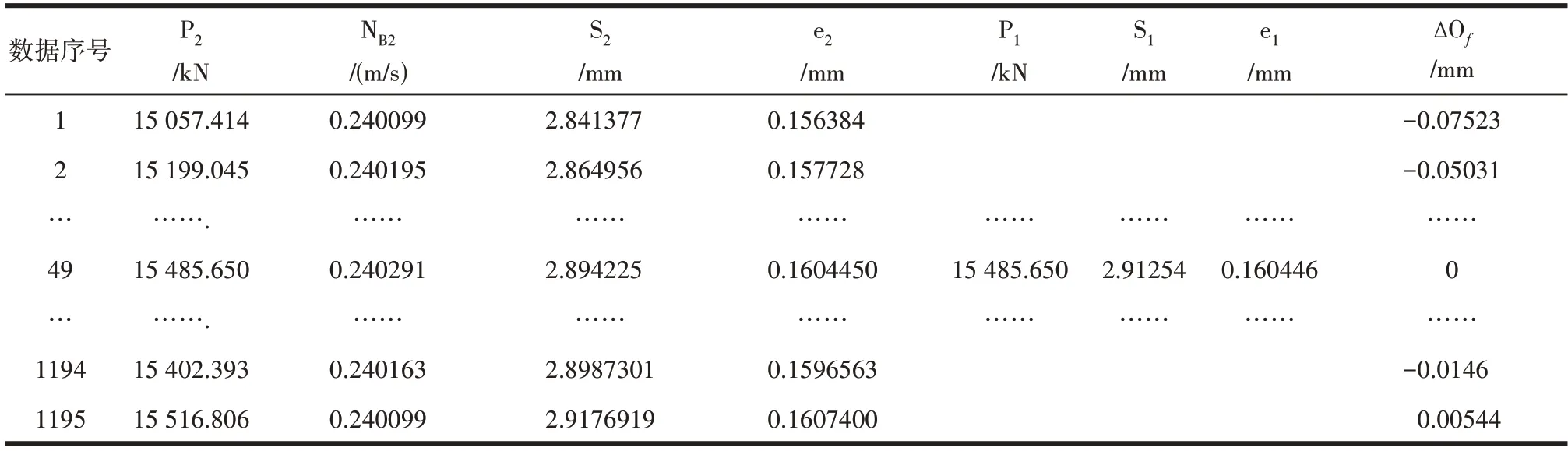
表2 采集数据处理过程一览表

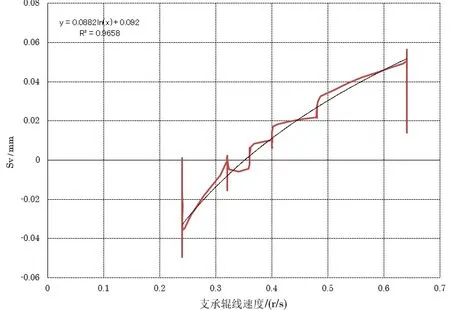
图6 15000kN下油膜-速度方程

4 轧制力补偿模型：KP-P关系方程

相对于速度的影响轧制力对油膜厚度影响要小得多［3］，同样具有非线性特征，在速度不变的情况下，可以通过轧制力补偿系数曲线KP-P对数方程来表示，通过不同轧制力下KP值回归得出。图7 清楚地表述了不同轧制力的ΔOf-NB曲线是不同的，每个轧制力都会对应一条自有的曲线，近年来各种研究方法产生了多种方程表达式和数学模型，其中依据现场测试的数据回归结果进行分析操作性强，直观性好，可信度高。在支承辊速度保持不变的情况下，令KP为同一支承辊速度下轧制力ΔOf-NB曲线对应的ΔOf值与零标时ΔOf0值的比值，称为轧制力补偿系数KP，（图8）假设KP-P的相关方程为：

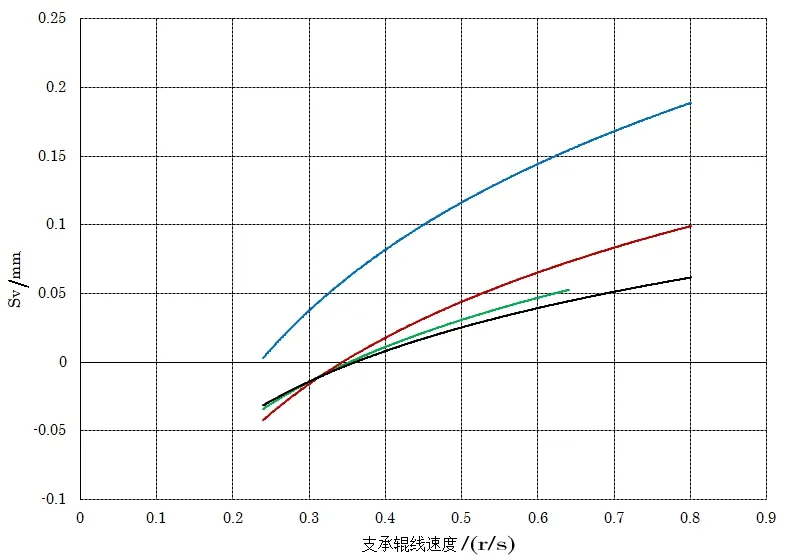
图7 各压力下的油膜-速度曲线

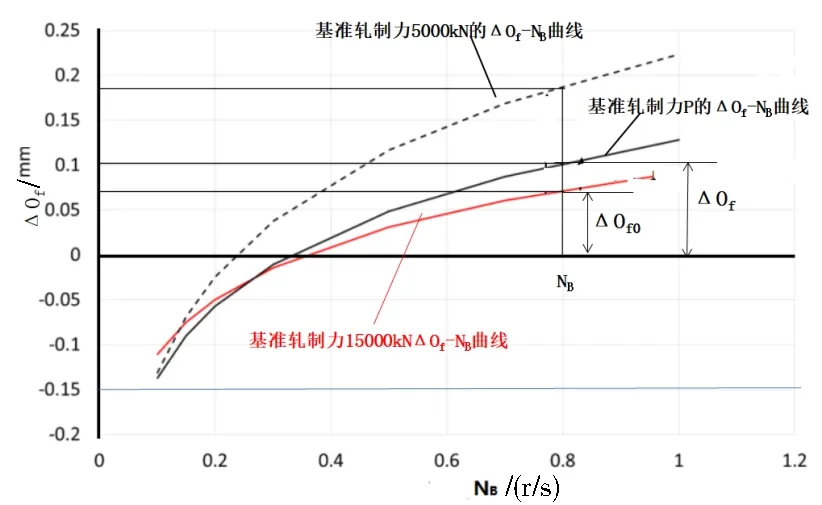
图8 ΔOf0、ΔOf取值示意图

式中选择零标轧制力15 000 kN的ΔOf0-NB曲线作为基准轧制力曲线ΔOf0，B0，B1为KP-P 方程的相关系数可以通过数据回归后求出（表5）。一般来说取采用对数拟合是为了使得数据平滑一些，可以使太过稀疏的数据变得不那么稀疏。

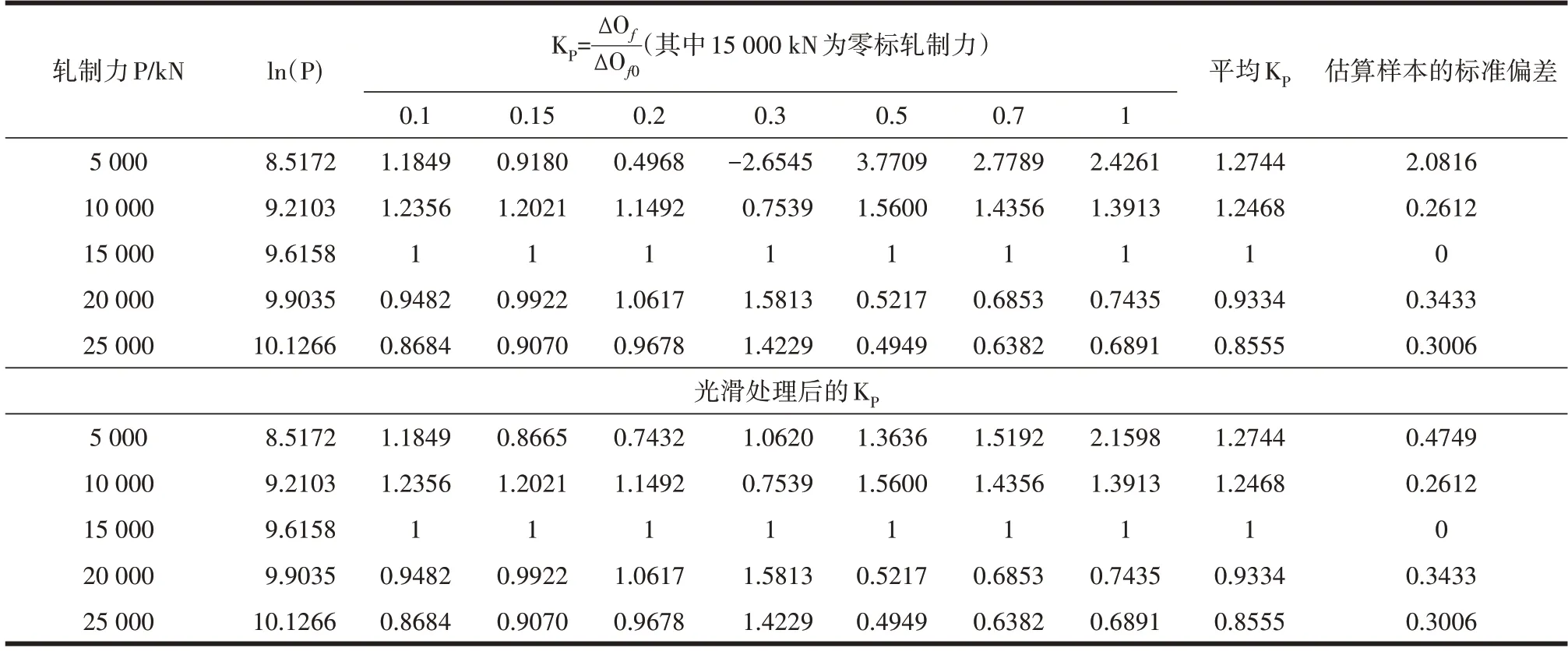
表5 Kp值的数据处理一览表

上表中5 000 kN对应的K5000平均值样本偏差较大，数据光滑处理后对Kp的平均值与轧制力P 数据回归可得相关方程（图7）：

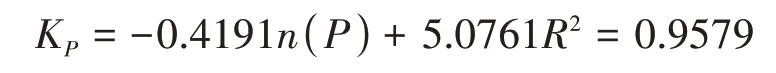
其中：B0=5.0761，B1=-0.4191

轧制前都要对轧机进行零标，一般情况都会采用零标轧制力作为基准轧制力，轧制力补偿系数因此是一个实际轧制力和零标轧制力的比例修正系数值，标定轧制力下轧制力影响系数为1.0。随着轧制力的增加修正量趋于减小。

5 实际油膜厚度补偿模型

从实际的角度来看，油膜厚度的形成与轧制力和轧制的速度有一定关系并且相互共同影响，在轧制辊缝校正时必须综合考虑这个影响。

根据式11、转化可得：

图9 KP-P曲线方程的数据回归

ΔOf0为零标时的ΔOf-NB曲线方程，以2250 热轧F1为例，轧制力速度影响模型是：

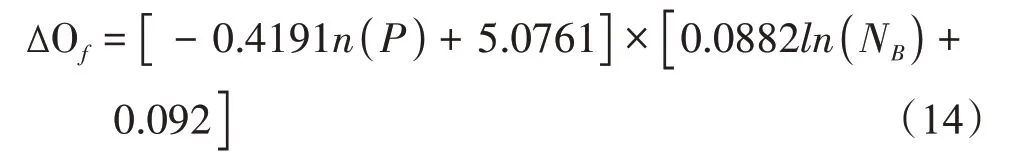
速度和轧制力的影响曲线存储轧制辊缝补偿模型中。在轧制过程中可以获得实际速度和轧制力下的速度补偿值ΔOf和轧制力补偿系数KP。最终的补偿结果由零标速度补偿方程和轧制力补偿系数方程相乘后获得。轧机带载延时6 s 后功能投入，轧机卸载后功能取消。

精轧机油膜厚度补偿功能在轧线程序中由一、二级自动化两部分组成。二级自动化系统完成油膜速度补偿曲线方程和轧制力补偿系数曲线构建，将速度补偿参数和轧制力补偿系数以数组形式下发到一级控制器中。一级自动化系统接收二级下发的速度和轧制力相关补偿参数，根据实际轧制速度和实际轧制力通过回归出的油膜补偿曲线得出油膜厚度变化值，完成油膜厚度的实际补偿值计算，与二级预补偿值相减后成为最终输出值修正辊缝设定。

陈东宁等［5］研究了通过空压靠得出雷诺方程求出相对油膜厚度的方法，并运用于AGC 控制中，首先通过最小二乘迭代法拟合出轧制力为2、3、4、5 MN整数时的雷诺方程的相关系数a，b：

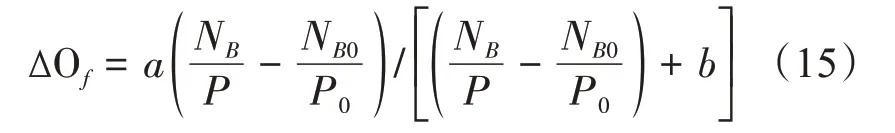
当计算的轧制力不是整数轧制力时，利用线性插值法，得到非整数下的相对油膜厚度值如式（16）所示。计算出油膜厚度变化量，然后反相加到压下位移调节中，对雷诺公式变形得到适合现场应用的修正模型来进行补偿，达到减小带钢厚差的效果。

实际上轧制力对油膜相对厚度NB/P 的影响是一条非线性的的曲线，因此用线性插值的方法求解，存在一定的误差，而本文采用的轧制力补偿曲线能够较好地弥补了这个问题。

6 结语

油膜厚度主要决定于支撑辊速度及轧制力，与支撑辊速度正比，与轧制力成反比。为了得到精确的影响必须分为速度影响和轧制力影响这两部分来考虑。支承辊速度对辊缝影响是非线性的，可以通过ΔOf-NB对数方程来表示，并通过零标回归得出，不必考虑轧制力的影响因素。轧制力对油膜厚度影响要小得多同样具有非线性特征，在速度不变的情况下，可以通过轧制力补偿系数曲线KP-P对数方程来表示，通过不同轧制力下KP值回归得出。AGC 油膜厚度控制模型中，综合轧制力和转速的变化之间关系和影响，将上述两个模型的乘积作为ΔOf=KPΔOf0轧制力、速度影响模型。兼顾了油膜厚度、轧制力和轧制速度之间的耦合、非线性关系，同时减少了线性插值法带来的误差。

油膜补偿是厚控系统中不可缺少的模型，只要模型精确，初始辊缝设定才会准确，厚度命中率就会提高。采用上述经过补偿的二级轧制模型对轧件厚度的控制效果特别明显。图10 是精轧机油膜补偿模型前后在轧制过程中轧件头部变薄以及通长尺寸波动情况得以明显改善。

图10 模型投入前后轧件效果比较