基于子结构的立加床身层级优化方法

李伟光，韩 林，刘少帅，刘福聪

（1.天津职业技术师范大学 机械工程学院，天津 300222；2.天津市高端智能数控机床工程研究中心，天津 300222）

0 引言

床身作为数控机床重要支撑基础大件，其结构振动特性对于整机的加工精度有着直接影响。如何优化床身的动态特性是目前工作难点之一。近年来众多工作者一直致力于实现床身结构尺寸的最佳优化方法研究[1-6]，通过优化改进方案、构建机床结构设计方法数学模型均获得了较好优化效果[7-9]。上述学者研究虽为床身结构优化提供众多思路，但大都基于整体宏观尺寸下的床身结构优化。

本研究基于床身局部结构动态特性，以某型立式加工中心床身为例，将床身内部筋板结构看作独立子结构。就其单独动态特性而言并不具备工程意义，但由于床身是众多子结构微元的集合，故子结构的局部动态特性必然与床身整体结构特性存在着联系[10]，以此进行机床床身结构优化，探究基于子结构床身优化过程中存在的一般规律，实现由床身的局部结构动态特性对床身整体的结构优化。

1 床身建模

原床身结构如图1 所示。如图1（a）床身呈T 型结构，高度H= 620 mm，尾部W1= 1420 mm，头部W2= 2320 mm，L1= 3253 mm，L2= 4300 mm。如图1（b）床身内部看作长方体子结构，a、b、c 表示三个方向上的尺寸，a×b×c= 460 mm × 460 mm × 315 mm。除上表明外，其余五个表面均开有230 mm ×230 mm 的方形流沙孔，筋板厚度为25 mm。由于整机低阶固有频率取决于基础大件，故此处拟对床身进行优化设计。由图1 可知，床身底部主要由子结构组成，为此首先提取子结构特征参数，在对子结构优化的基础上，重新布局床身底部筋板，从而实现整个床身静动特性的提升。

图1 原床身结构示意图

2 子结构优化

子结构具体尺寸参数如图2 所示，其中d为圆孔直径，l为开孔面短边长，h1、h2为方孔边长，t为壁厚。以独立单元子结构进行动态特性分析。

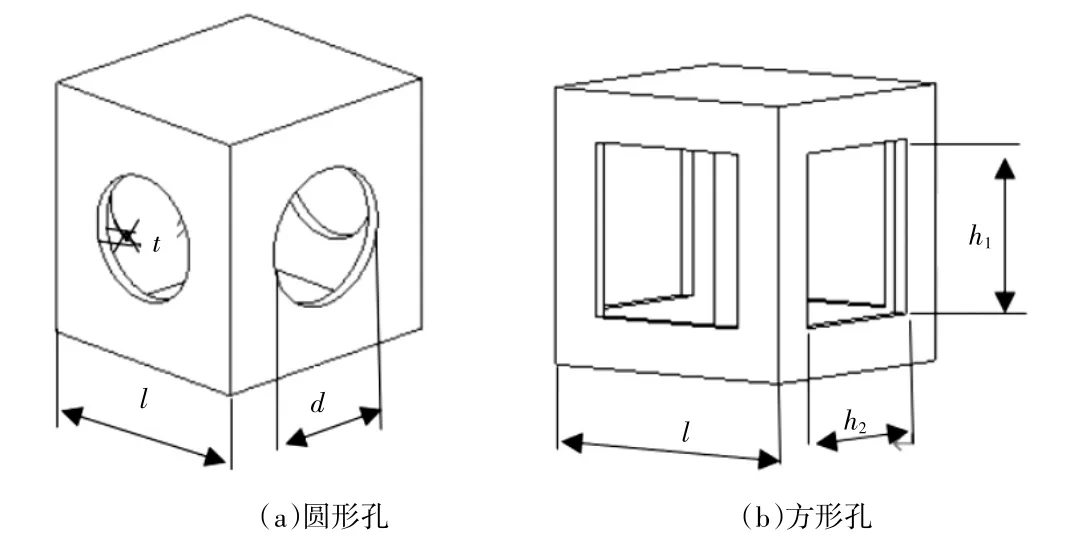
图2 子结构示意图

2.1 子结构轮廓尺寸动态特性

本研究主要探讨自由度、轮廓尺寸、开孔形状对子结构固有频率的影响规律。其中，垫块支撑为垂向约束，地脚支撑为全约束，无约束即忽略床身实际约束为对照组。关于轮廓尺寸，考虑整机加工范围设床身高度不变（a=b= 460 mm），c为变量。开孔形状取两种，一为方孔，另一种为圆孔，如图2 子结构五面开孔，两种形状开孔面积一致。c取300 mm ～ 620 mm、步长40 mm，对应的c/b为0.65 ～ 1.35，具体方孔尺寸为230 mm，圆孔直径为260 mm，面积为53 093 mm2，壁厚25 mm。在不同约束方式和流沙孔形状的条件下，子结构边长比c/b对首阶固有频率的影响规律如图3 所示。

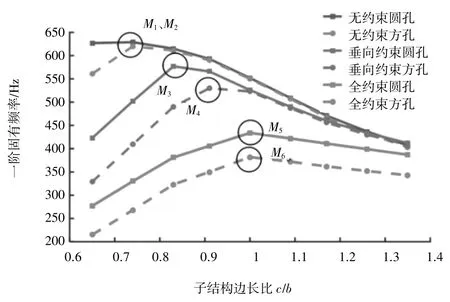
图3 开孔形状、支撑方式对一阶频率的影响

不难看出，由于圆孔不具备方向性，振动特性的扩散相较于方孔更加的均匀，因此一阶频率明显高于方孔；且子结构动态特性受实际约束状态影响很大，随子结构约束自由度增加一阶频率下降；两种开孔方式在同一c/b值下，较全约束，垂向约束有更高一阶频率；一阶频率随c/b的增大出现明显拐点，如图中M1～M6，定义拐点处c/b值为理想边长比。理想边长比前，c/b值对一阶频率有较高灵敏度水平；理想边长比后，一阶频率下降速率放缓。垂向约束中，圆孔先于方孔在M3、M4点到达理想边长比（c/b= 0.8 ～ 0.9）；全约束中，圆孔和方孔同步在M5、M6点到理想边长比（c/b= 1），但由于正六面体的高度对称性，使其低阶频率相对集中，在选择地脚式支撑时应使边长比c/b介于1 ～ 1.2。

对上述子结构施加一自激稳定简谐力，以首阶频率处最大谐响应幅值δmax为目标响应，求得各子结构未开孔面上一点位δmax变化曲线，如图4 所示。

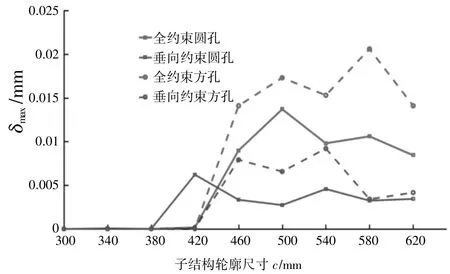
图4 子结构约束形式对一阶谐响应幅值的影响

由图4 可以看出，参数c≤420 mm 时，各子结构首阶频率下的δmax很小；c＞420 mm 时同一开孔方式下，垂向约束对于自激振动的响应优于全约束形式，且不论哪种约束形式，δmax值圆孔均小于方孔，表明不同支撑方式下圆孔结构均具有良好的减震效果。

2.2 子结构排沙孔尺寸动态特性分析

根据3.1 分析结果，选用垂向约束进一步探究开孔尺寸对子结构动态特性的影响。在改变排沙孔尺寸与子结构边长的比值时（即d/l 或h/l），为避免开孔尺寸大于所在面边长，其中l= min{a，b}或min{a，c}或min{b，c}。圆孔、方孔的理想边长比c/b依次为0.83 ～0.91、0.91 ～ 1，取c/b= 0.91（c= 420 mm）。基于此改变d/l或h/l值，探究开孔尺寸对子结构一阶频率的影响曲线如图5 所示。

图5 开孔尺寸对一阶频率的影响

可以看出N1、N2点前，d/l值对一阶频率影响不显著，主要是由于N1、N2点前，随开孔尺寸增加，子结构质量减轻、刚度减弱，但二者同时给固有频率带来的影响不明显所致。随开孔尺寸持续增加，即超过N1、N2点时，剩余材料的刚度也随着明显下降，对固有频率的影响程度高于质量减轻带来的影响，一阶频率下降速度明显加快。由此可知，圆孔在振动稳定性及受力均匀性上都要优于方孔。

2.3 子结构壁厚动态特性分析

筋板壁厚过薄抗变形能力弱，壁厚过大铸造时内部冷却速度放缓容易产生棉孔。原子结构壁厚t=25 mm，因此t取[10 mm，45 mm]。这里仍以3.2 中的边长比c/b=0.91、初始开孔尺寸d=260 mm、h1=h2=230 mm 为研究对象，探究壁厚t与开孔面积比值对一阶频率的影响，如图6 所示。

图6 壁厚t 与开孔面积比值对一阶频率的影响

可以看出圆孔动态特性优于矩形孔，随t/S1/2的增大，Q1、Q2点前一阶频率有明显上升，Q1、Q2点获得较高一阶频率，随后当壁厚t超过图中两点对应值时，再增加壁厚没有意义。如3.2 讨论，开孔尺寸为d/l= 0.5、h/l= 0.4 时最佳，该比值下对应的最佳壁厚t分别为25 mm、19.4 mm。

3 优化前、后床身静动态特性分析

以低阶频率为评价指标，同时计及静态变形、最大应力。优化目标描述为：在满足强度条件下，降低静态变形提高低阶频率。根据前述优化方法，指定床身子结构理想边长比（a×b×c=460 mm× 460 mm×420 mm）；根据不同开孔面短边长l 分别选用d1=210 mm，d2= 230 mm 的排沙孔；且圆孔在d/l= 0.5时对应的最佳壁厚t= 25 mm。图7 为优化前、后床身内部结构，明显地筋板数量整体上有减少，结构比原床身简单。

图7 优化前、后床身内部结构

3.1 静态特性

将模型导入有限元，床身材料HT300，λ= 0.2，ρ= 7.3 × 10-6kg/mm3，E= 1.3 × 105MPa。采用四面体网格划分，整体尺寸为10 mm，对立柱、导轨接触面等重点关注区域细化为5 mm，床身垫块处施加垂向约束。

床身受到立柱、主轴等重力G1= 1.150 × 105N，床身与立柱接触面积S1= 0.741 m2，施加载荷P1：

通过Creo 质量属性分析，立柱重心落在头部W2

区域，故立柱接触面不受扭矩作用。利用有限元进行静力分析，具体结果见表1。

表1 床身原结构和优化结构静态特性分析结果

从表1 可以看出，优化后床身抗变形能力有提升，床身所受应力分布与原床身基本一致且最大应力有所减小，优化后的床身质量增加约2.7%在可接受范围内。

3.2 模态分析

床身的振动特性只体现在低阶模态中。通过Workbench 获取优化前后前四阶固有频率及振型，见表2。

表2 优化前、后模态对比

从表2 可以看出，原床身流沙孔由方形改为圆形后，前四阶频率均有不同程度的提升，进一步验证了3.2 分析结论的正确性。优化后床身前四阶频率均有大幅提升，一阶频率提升幅度也达13%，说明子结构的局部动态特性与床身整体结构特性存在联系，验证了子结构-床身层级优化方法的可行性。

4 结语

用基于子结构-床身层级的优化方法验证了立加床身动态优化过程中的一般规律。通过对床身子结构分析，探究了不同约束形式下固有频率走势和谐响应振幅的影响曲线，并以低阶频率为评价指标，实现床身结构的动态优化。在此过程中结合参数分析，选取结构设计参数，对参数模型分析，以优化的子结构尺寸指导床身结构的整体布局。从新型床身优化效果看，子结构-床身层级优化方法是合理有效的，设计流程具有一般性，可为床身的结构优化提供借鉴，还可推广至此类机床床身的正向设计中。